带电球面和带电球体电场强度和电势分布求解探讨*①
2016-09-05刘敏敏俎凤霞
刘敏敏 俎凤霞 吴 涛
(武汉工程大学理学院 湖北 武汉 430205)

带电球面和带电球体电场强度和电势分布求解探讨*①
刘敏敏俎凤霞吴 涛
(武汉工程大学理学院湖北 武汉430205)
在大学物理静电场的教学中,与球形有关的问题很典型,比如带电球面和带电球体周围空间的电场强度和电势分布问题,不同电荷密度分布带电球体周围空间的电场强度和电势分布的求解问题,本文对这些球形带电体系进行分析探讨,分别根据定义式求解和高斯定理求解,并找出了其规律式和特点.
带电球面带电球体电场强度电势
在大学物理静电场的教学中,电场强度和电势是反映静电场本身性质的重要物理量[1~7],目前已经有了相当多的讨论[3~7].在电场强度和电势的探讨和求解中,与球形有关的问题很多,比如带电球面周围空间的电场强度和电势分布问题,不同电荷密度分布的带电球体周围空间的电场强度和电势分布的求解问题,然而在实际的教学中,我们发现学生在理解和计算的时候会在物理思想和数学计算上存在疑惑,本文将对这些球形带电体系进行分析探讨,并找出其规律和特点.
1 真空中均匀带电球面的电场和电势分布
设均匀带电球面的总体带电量为q,其球半径为R,电荷面密度为σ,求解此球面内和球面外两个部分的电场强度分布,可以采用两种不同的方法:(1)点电荷电场强度叠加法;(2)高斯定理.电势则可以在此基础上进行求解.下面分别进行探讨.
1.1点电荷电场强度叠加法
对于均匀带电球面,由于场强具有球对称性,只需要求解其径向的电场强度即可.首先将其看成是沿某一直径方向上,无数个半径连续变化的圆环的叠加,这样其电场强度将是这许多圆环电场的叠加, 利用半径为a的圆环的中轴线上P点的电场强度的结论
即可求解.
如图1所示,环带半径a=Rsinθ,环带宽为Rdθ,环带的面积为2πR2sinθdθ,环带带电量
则环带在P点处产生的场强为
(1)

图1 均匀带电球面示意图

(2)
(3)
球外一点
(4)
球内一点
(5)
1.2高斯定理求解
取同心球面为高斯面,如图2所示.
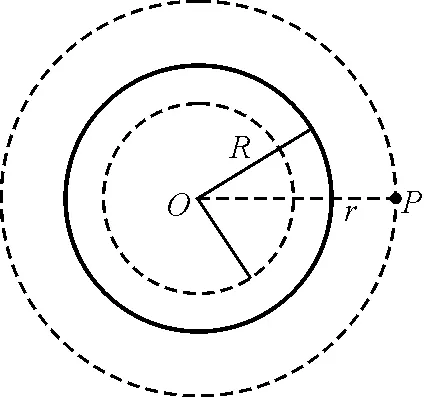
图2 均匀带电球面高斯面示意图
由对称性可知,高斯面上的电场强度大小处处相等,方向为半径方向,因此有
(6)
则电场强度
(7)
可以看到对于具有高度对称性的均匀带电球面,利用高斯定理求解其内外空间的电场强度是非常方便的,在数学计算上也相对简单得多.然而要从本质上直观逻辑性地去理解电场强度的性质,则电场叠加原理是容易被理解的,只是数学计算比较复杂,在大学物理的教学中需要学生的数学基础相对较好.
1.3电势的求解
静电场中P点的电势等于电场强度从该点开始沿着任意路径到零势点的线积分,这里取无穷远处电势为零,因此球外距球心为r处一点的电势
(8)
距球心为r处球内一点
(9)
整个球面以及球面内等势.
2 真空中带电球体的电场强度和电势分布
带电球体类型的问题中最典型的就是:真空中有一半径为R的带电球体,其电荷体密度分布为ρ=Arn,A为一常量,其电荷密度分布是半径的幂函数.试求球体内外的场强分布.我们在实际的教学中通常都是将幂n具体化,例如n=1,0,-1,2等等,对其逐一进行计算,其实这类问题可以一次求解出规律式,然后再针对具体的情形讨论.简述求解过程如下.
2.1高斯定理求电场强度
由于具有球对称性,方便利用高斯定理求解,设整体带电量为q,选择过P点同心的球面为高斯面,如图3所示,若高斯面在球内则用qin表示所包围的电量,由高斯定理可得
(10)

图3 具有球对称的带电球体示意图
球外的电场强度求解很简单,比较难的是求解球内的电场强度.求解球内电场强度关键在于求解高斯面包围的电量qin.由于电荷密度是径向的幂函数,因此选取薄球壳为积分元,进行积分求电量
dq=ρdV=Arn4πr2dr
(11)
(12)
当n>-3时,有
当n≤-3,则
积分无解,即:
(1)n=-3时,由n+3=0可知分母为零,积分无解;
(2)当n<-3,此时rn+3在分母上,积分从r=0开始,因此分母出现为零的情形,所以积分无解,从物理本质上来说此时对应着电荷几乎全部集中在球心处的情形,球心处的密度无穷大.
因此,对于可以求解的n>-3的情形,体系的电场强度为:
球外距球心为r处电场强度大小
(13)
球内距球心为r处电场强度大小
(14)
2.2电势的求解
根据电势的定义,带电球体球外P点
(15)
球内一点
(16)
对于不同的n的取值,直接代入规律式即可得到电场强度和电势的分布情形,而且,n还可以不仅仅只取整数值,对于n取分数值,该规律式同样成立.
3 小结
本文讨论了真空中均匀带电球面周围空间的电场强度和电势分布问题以及随径向不同密度分布的带电球体周围空间的电场强度和电势分布的求解问题,对这些球形带电体系进行分析探讨,并归纳总结了其场强和电势的计算规律表达式及特点.
1张三慧,等.大学物理学(第3版).北京:清华大学出版社,2009
2胡亚联,吴峰.大学物理学.北京:科学出版社,2010
3周瑞雪.关于圆盘状物体的几个物理量的计算.物理与工程,2014,24(5):51~58
4景义林.无限大圆平面稳恒发散电流产生的磁场.大学物理,2015,34(4):13~15
5郭浩,陈钢.线电荷与带有半椭圆柱凸起的接地平板系统的电势.大学物理,2014,33(11):9~11
6林焰清,陈钢.线电荷与接地椭圆柱形导体系统的电势.大学物理, 2009,28(8) : 25~27
7阳喜元,蔡新华,吴丹.微元法研究均匀带电体的电场分布.广西物理,2016,29(3),34~37
Solution Discusses on Electric Field Intensity and Potential Distribution of a Charged Spherical Surface and a Charged Sphere
Liu MinminZu FengxiaWu Tao
(School of science, Wuhan Institute of Technology, Wuhan,Hubei430205)
In the teaching of electrostatic field in university physics, problems related to the spherical is tipical, such as eletric field intensity and electric potential distribution problem for a charged spherical surface or a charged sphere with different charge density. This paper discusses and analyses these problems, and find out the general law and characters with using the definition and the Gauss theorem.
a charged spherical surface; a charged sphere; eletric field intensity; electric potential
刘敏敏(1981-),女,博士,讲师,主要从事物理教学以及光学和原子与分子物理方向的研究.
2016-01-17)
①*武汉工程大学科学研究基金项目,项目编号:K201422;武汉工程大学教学研究基金项目“科研促进教学,深化大学物理课程体系改革”,项目编号:X2014037
