基于压力钢管地下埋管设计的相关讨论

曾　越

(广东水利电力职业技术学院，广州 510635))



基于压力钢管地下埋管设计的相关讨论

曾越

(广东水利电力职业技术学院，广州 510635))

根据《水电站压力钢管设计规范》 (DL/T 5141—2001)提供的地下埋管计算方法，笔者在实际设计计算中遇到了其它条件相同时围岩覆盖厚度较大的埋管壁厚反而较大的反常现象。文章深入分析了此种反常情况，原因在于初始假定的围岩分担的内水压力值P2的取值存在较大的不确定性，未能从逻辑上理顺P2与缝隙值、围岩单位抗力系数、钢管本身的力学特性和上覆围岩厚度的相互关系，并提出一个可以综合考虑上述各影响因素的新概念K0c，使得地下埋管结构计算过程更为合理清晰。

压力钢管设计规范；地下埋管；覆盖围岩厚度；判别条件

根据《水电站压力钢管设计规范》，从理论角度而言，在相同的围岩地质条件下，覆盖围岩厚度越大，相应的围岩分担最大内水压力也会随之增大，地下埋管的计算厚度应相应减小[1]。但笔者在实际工作中却遇到了与之相反的现象，令人十分不解。为弄清事情的因由，笔者通过一个设计实例对《水电站压力钢管设计规范》所列的地下埋管计算方法进行了重新推演，找到了问题症结所在，并提出了相应的解决方法。

1　问题的起源

某抽水蓄能电站某部分地下埋管段管壁厚度计算，该管段的计算参数如下表1所示：

表1　某电站部分埋管段计算参数表

满足围岩覆盖厚度判别条件1，即Hτ>6r5。

依据规范，进行围岩分担最大压力(此时δ2取值应为0)的试算:

不满足围岩覆盖厚度判别条件2，此时令：

P2=γrHrcosα(1+ηrtan2α)=0.941MPa

计算管壁厚度为：

然而，同样地质条件下，假定此段能够满足覆盖围岩厚度判别条件2，按规范公式计算所得到的管壁厚度为：

=31.4mm>t=16.9mm

从上述计算结果可知，覆盖围岩厚度能满足要求时钢管壁厚却较大，覆盖厚度不能满足要求时，钢管壁厚反而较小，且二者差值较大，十分反常。从理论角度而言，针对此段埋管，当满足围岩覆盖厚度判别条件时，钢管壁厚应当<16.9 mm才是符合逻辑的[2]。

基于此，文章立足于《水电站压力钢管设计规范》，从地下埋管的力学分析着手，分析围岩分担内水压力的公式，对围岩条件较差时，管壁厚度的计算方法尤其是围岩覆盖厚度判别条件2进行探讨。

2　问题的分析

地下埋管计算简图如下图1所示。

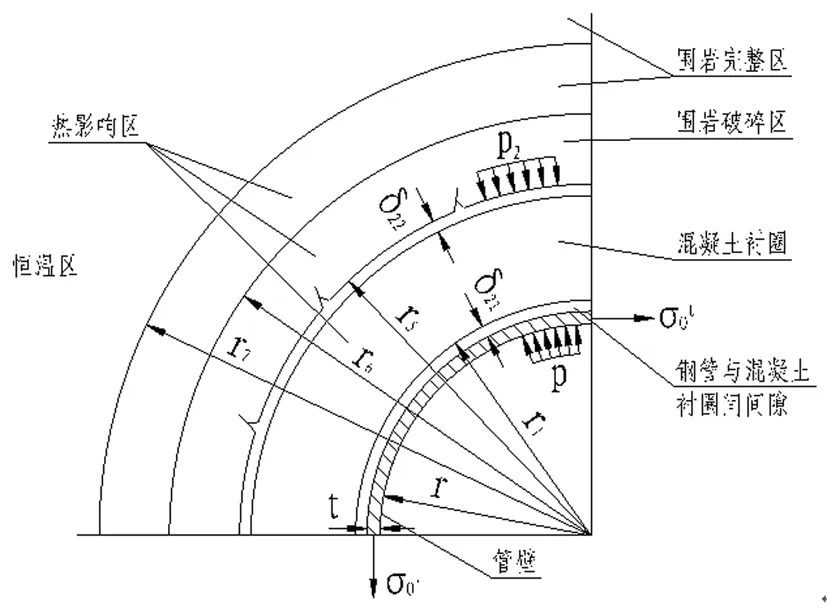
图1　地下埋管计算简图

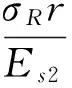
试算围岩分担的内水压力P2的过程为：将管壁的构造厚度作为管壁的最小厚度，取围岩单位抗力系数最大可能值，并取最高水温下钢管冷缩缝隙值，得到围岩分担的最大内水压力值P2，如下式(1)和式(2)所示。

(1)

(2)

上式(1)、(2)中：P2为围岩分担的最大内压，MPa;p为内水压力设计值，MPa;σθ1为内压作用下钢管最小环向正应力，MPa；rs为混凝土衬砌外半径，mm，即隧洞开挖半径;K01为围岩单位抗力系数最大可能值，MPa，式中1000所带单位为mm；δs2为最高水温下的钢管冷缩缝隙值，mm；Es2平面应变问题钢材的弹性模量，MPa[3]。

从上式(1)和式(2)可知，管壁厚度t本是未知的，由于需要知道P2的大小，故必须先假定t的大小，由上式(2)计算得出σθ1的值，再代入式(1)，得出P2的值。从经济性角度考虑，为充分发挥围岩的作用，应该取用较小的壁厚(构造厚度)和较大的围岩单位抗力系数K01。但是，由于管壁的构造厚度受到管径的影响，构造厚度t的取值本身就有一定的随意性，而取用K01本身也不是逻辑严谨的选择，因为主观上取用了K01，但实际上围岩未必能够像主观想像的那样发挥了如此大的作用；另外，δs2的值由于受到资料本身的限制，也不易取得准确值；故在3个影响因素都存在不确定性的情况下试算得出的围岩分担的最大内水压力值P2是完全可能存在人为误差的[4]。

为了更充分透彻地说明问题，对诸公式推理如下：

由于地下埋管沿管轴线方向的变形远<管截面内的变形，故一般将地下埋管按平面应变问题考虑。管道在内水压力作用下，首先均匀扩大，直至将缝隙填满，继而与衬砌、岩壁相接触，共同变形。假设围岩分担的最大内水压力值为P2/MPa[5]。

则相应的围岩径向位移为：

(3)

式中；K0为岩石单位抗力系数较小值，MPa ，式中1000所带单位为mm。

则管道的径向位移为：

(4)

式中：δ2为钢管与混凝土衬砌、混凝土衬砌与围岩之间存在的缝隙值，mm。

在实际设计时，从经济性角度考虑，当管道发生了上述位移时，其环向应力应该达到钢材的抗力限值σR，而钢材的环向应力σR与径向位移△的关系为：

(5)

式中：σR为钢材抗力限值，MPa。

由式(4)和式(5)可得：

(6)

对式(6)整理，可得:

(7)

从式(7)可以看出，理论上P2与K0成正比。但是，由于实际工程中覆盖围岩厚度总是有限的，因此，围岩所分担的最大内水压力应≤围岩的重力及侧向压力所能提供的压力值，该值的大小为P02=γrHrcosα(1+ηrtan2α)，即总应该有P2≤P22。围岩能够分担的最大内水压力值P2与K0的关系曲线见图2。

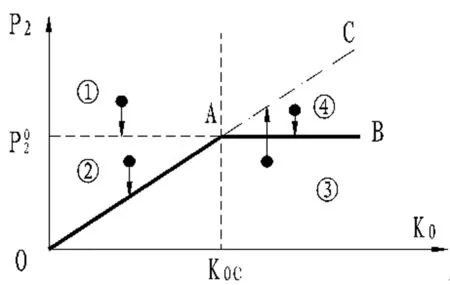
图2　围岩分担最大内水压力计算简图

该曲线OAB由一临界的K0C分为前段OA和后段AB，共两段。

从图2可以看出，即使覆盖围岩厚度为无穷大，若围岩单位抗力系数K0的值为0，围岩能够分担的最大内压P2仍然为0；只有当K0的值也趋于无穷大时，围岩分担的最大内压才会趋于无穷大。

若覆盖围岩厚度一定时，则围岩所能承担的内水压力P2是有限的，其值大小应为P02=γrHrcosα(1+ηrtan2α)。

由图2可以看出，若试算得出的P2位于①区或④区，按照规范的规定，P2的最终取值应该按照下式(8)取值；若试算得出的P2位于②区或③区，按照规范的规定，P2的最终取值应该按照下式(9)取值。显然，若试算得出的P2位于①区或③区时最终P2的取值已经超出了围岩的实际承担能力，过高的估算了围岩分担的最大内水压力，因此，试算得出的P2是不合理的[6]。

P2=γrHrcosα(1+ηrtan2α)

(8)

(9)

上式(8)、(9)中：γr为围岩重度，N/mm3；Hr为垂直管轴最小覆盖厚度，mm；α为管轴与水平面夹角；ηr为围岩侧向压力系数。

3　问题的解决

笔者认为出现上述不合理情况的根源在于围岩分担的内水压力P2的选取具有随意性，没有厘清围岩本身的分担能力与实际分担的内水压力P2的关系。围岩的分担能力，不仅与覆盖围岩厚度有关，而且与围岩本身的抗力系数有关[7]。过高地估算围岩的分担能力是不安全的，将会给工程留下隐患。因此，只有明确了围岩的分担能力，才能最大限度地利用围岩的分担能力，从而达到安全和经济的双重目的。鉴于此，笔者提出以下考量方法。

在对地下埋管厚度进行计算时，先不考虑试算P2，而是令：

(10)

整理，得：

(11)

K0c的物理意义在于：在覆盖围岩厚度一定、钢管材质一定的条件下，围岩能够充分发挥其作用所需要的最小单位抗力系数。因此，若实际的围岩单位抗力系数K0≥K0c，则在此覆盖围岩厚度及钢管材质条件下，围岩能够充分发挥其作用，围岩分担的内水压力值P2及钢板厚度t应按下式(12)进行计算；若实际的围岩单位抗力系数K0

当K0≥K0c时：

P2=γrHrcosα(1+ηrtan2α)

(12)

当K0

(13)

从上式(12)、式(13)可以看出，当满足缝隙判别条件和围岩覆盖厚度判别条件一时，围岩总是能够分担一定的内水压力，至于能够分担多少，则与其本身的分担能力有关。因此，围岩覆盖厚度判别条件二应该表述为围岩本身的分担能力的计算，可以由围岩的实际单位抗力系数K0与K0c进行比较得知。该判别条件综合考虑了围岩的地质条件以及围岩覆盖厚度的大小，更能体现围岩分担内水压力的能力，并省略了P2的试算过程，使得计算过程更为合理清晰[8]。

围岩分担的内水压力P2，既与压力钢管覆盖围岩厚度相关，又与围岩单位抗力系数K0相关，同时还与最终所采用的钢管壁厚相关。从图2可知，折线OAB就是围岩所能分担的最大内水压力的边界线，沿此边界线即是充分地利用了围岩的分担能力，是最经济的。

4　结论及建议

围岩的分担率的划分对工程安全性有着重大影响，过大的估算围岩的分担率将会给工程安全埋下隐患。影响围岩内压分担率的主要因素为缝隙值δ2与围岩的单位抗力系数。当围岩覆盖厚度一定时，在保证施工质量的前提下，围岩分担率主要取决于围岩的单位抗力系数K0的大小。将围岩单位抗力系数K0纳入围岩的分担能力计算具有实际的工程意义。因此笔者建议压力钢管规范修编时对埋管部分覆盖围岩判别条件2予以重新考虑。

[1]中华人民共和国国家经济贸易委员会.DL/T 5141—2001水电站压力钢管设计规范[S].北京：中国电力出版社出版，2001.

[2]侯建国，李春霞，安旭文，等.水电站地下埋管围岩内压分担率的统计特征研究[J].岩石力学与工程学报，2003，22(8)：1334-1338.

[3]张伟，张瑾，杨绿峰，等.考虑应变硬化的水电站压力钢管整体安全评估[J].水利水电技术，2012(12)：82-85.

[4]李铮，李宏恩，袁启旺，等.阶跃函数模型在龙江水电站压力钢管监测中的应用[J].水电能源科学，2011(07)：56-59.

[5]朱万旭,马倩,马聪,等.用于建筑结构预制拼装的灌浆套筒连接技术[J].四川理工学院学报(自然科学版),2013(04):71-75.

[6]诸葛睿.关于压力钢管设计规范的讨论[J].云南水力发电,2003(01):38-41.

[7]黄发林,潘益斌,冉荣庆.电站压力钢管设计方法探讨[J].中国科技信息,2013(07):74-75.

[8]翟振华,冉荣庆,潘益斌.水电站地下压力埋钢管抗外压设计探讨[J].浙江水利科技,2007(05):20-24.

Discussion on Underground Penstock Design

ZENG Yue

(Guangdong Water Resources & Electric Power Technical Collage，Guangzhou 510610，China)

According to the calculation method of penstocks presented in Design Code on Penstocks of Hydropower Stations (DL/T 5141—2001)，an abnormal phenomenon that penstocks with very thick covering layer of surrounding rock have thick pipe wall when other conditions are the same appears during actual calculation process.This paper analyzes deeply the reason causing the abnormal phenomenon and it is because the preliminarily assumed value of internal water pressure P2 borne by the surrounding rock has great uncertainty and the relationships between internal water pressure P2 and fissure value，unit elastic resistance coefficient of surrounding rock，mechanical properties of penstock，thickness of overlying surrounding rock cannot be rationalized logically.Therefore，this paper puts forward a new concept K0c which can consider comprehensively all influencing factors mentioned above and make the calculation process of underground penstocks more rational and clear.

design specification for steel penstocks of hydroelectric stations；underground penstock；overburden thickness of surrounding rock；judgment condition

1007-7596(2016)05-0076-04

2016-03-15

曾越(1975-)，男，广东阳春人,讲师，研究方向为水利工程。

TV732.41

B