渗透思想方法 加强学科育人

刘桂华

(山东省昌乐一中， 潍坊　262400)



渗透思想方法加强学科育人

刘桂华

(山东省昌乐一中， 潍坊262400)

数学的思想方法是数学的灵魂与精髓，在数学课堂教学中重视思想方法，不仅可以提升数学课堂教学效率，减轻学生的学习负担，还有利于培养学生的应用意识和创新意识．

一、如何渗透思想方法

要加强数学思想方法的渗透，教师在平时的课堂教学中可以从以下几个方面入手．

第一，在数学内容准备和概念、定理、公式的教学中渗透数学思想方法．在概念的引进过程中，应注意：(1)解释概念产生的背景，让学生了解定义的合理性和必要性；(2)揭示概念的形成过程，让学生综合概念定义的本质属性；(3)巩固和加深概念理解，让学生在变式和比较中活化思维．例如，教授二次函数区间最值时，可以先让学生完成如下较简单的问题．

画出函数y=-x2+4x-2的草图，并求出：

(1) 在区间[0，3]上的最大值是________，最小值是________；

(2) 在区间[-2，1] 上的最大值是________，最小值是________；

(3) 在区间[4，6] 上的最大值是________，最小值是________．

然后，让学生总结出求对称轴固定、区间固定的二次函数的最值的关键．即确定函数在区间内的单调性，再继续研究含字母的最值来求f(x)=x2+ax+3在区间[-1,1]上的最小值h(a)．这样学生很自然地就想到了分三种情况讨论．在这个过程中，学生潜意识里就运用了数形结合及分类讨论的数学思想解决了比较困难的问题．进而再求最大值并对两类最值进行规律总结．这样的问题引导能更好地培养学生分析问题的能力以及逻辑推理能力，通过规律方法的总结形成求二次函数区间最值的模型，再遇到此类问题学生就有章可循了．

第二，在自主、合作探究学习过程中领悟和掌握数学思想方法．在平时教学中注重依据基本数学思想，在解题时注重与学生分析、探讨解题思路与策略，在解题后引导学生小组合作进行总结，如本题应用哪些知识或概念，利用哪些基本技能，体现了哪些数学思想方法，还有哪些解法(一题多解)，还有哪些题可借助本题的解法(多题一解)．经过这样的自主探究、合作学习，能大大拓宽学生的解题思路．在探索过程中，重要的是让学生真正领悟隐含于数学问题探索中的数学思想方法，使学生掌握关于数学思想方法的知识，对这样的“知识”消化，并吸收具有“个性”的数学思想方法，逐步形成应用数学思想方法指导思想活动．例如学习导数的应用求解含参函数单调区间问题,求导之后可转化为求解含参一元二次不等式问题.在解题过程中通过多题一解就渗透了化归与转化的思想，将未知化已知，将高次化低次；复合函数问题利用换元法转化为两个基本初等函数解决．例如潍坊市(2016)高一上期末试题：

某工厂经过市场调查，甲产品的日销售量P(单位：吨)与销售价格x(单位：万元/吨)满足关系式

(其中a为常数).已知销售价格4万元/吨时，每天可售出该产品9吨.

(Ⅰ)求a的值；

(Ⅱ)若该产品的成本价格为3万元/吨，当销售价格为多少时，该产品每天的利润最大？并求出最大值.

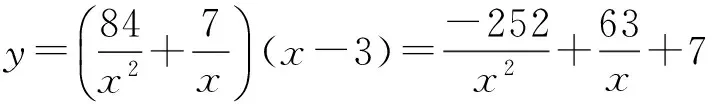
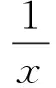
还有在立体几何的教学中常用到将空间问题转化为平面问题解决．直线与圆锥曲线问题的条件如：线段相等转化为中点垂直，利用数量积解决；夹角问题转化为两直线的斜率关系解决等．

第三，在知识的归纳总结和复习中概括数学思想方法．在平时教学复习中，要以思想方法贯穿整个教学过程，将各个知识点，引导学生在解题训练过程中以数学思想为主线，并进行知识点概括与归纳整理，从不同内容、不同角度、不同问题、不同方法中寻找同一思想．把数学思想方法纳入教学计划中，有目的、有步骤地引导学生参与数学思想方法的提炼、概括的过程．对于习题的选择不可以条块分割、泾渭分明，应在知识网络的交会处选题，有意识地设计隐含着数学思想方法的习题、高频率再现，精心安排，恰到好处地点拨．特别是章节复习时，在对知识复习的同时，将统领知识的思想方法概括出来，增加学生对数学思想方法的应用意识，从而有利于学生更透彻地理解所学知识，提高独立分析、解决问题的能力．例如学习函数零点问题时，要充分利用函数与方程的思想进行函数零点、方程的解、图像与x轴的交点的横坐标三者之间的转化．

A.4B.3C.2D.1

分析：函数h(x)的零点个数，即方程f(x)-g(x)=0的解的个数，即函数f(x)与函数g(x)交点的个数，这样就通过画函数f(x)与函数g(x)图像找到交点个数．答案B.

当然这个过程中也利用了转化及数形结合的思想．又如，由不等式恒成立求字母取值范围的常用方法有：最值法、分参法；求函数最值问题常用的方法是：单调性法、配方法、均值不等式法、导数法．只要我们学会了这些方法，按知识—方法—思想的顺序提炼数学思想方法，就能运用它们去解决成千上万同类的问题．

数学思想方法的教学不可能一步到位，是循序渐进的过程，因此在数学课堂教学中教师要按照“逐步理解、不断重复、自觉应用”的顺序来进行数学思想方法的教学．只有经过反复训练才能使学生真正领会．形成自觉运用数学思想方法的意识，必须建立起自我的“数学思想方法系统”，这更需要一个反复训练、不断完善的过程．在寻找解题思路时要能自觉地使用数学思想方法，尤其是要掌握数形结合的条件与分类讨论的标准等．最后，通过对自己解题的反思、总结，更深刻地领会其中的数学思想方法，从而灵活地运用数学思想方法进行解题．

二、加强学科育人

为了更好地做好学科育人工作，在日常的教学工作中还要注重以下三个方面的工作．

第一，深刻认识学科教学内容在培育核心素养上的作用和价值．

(1)通过学习、研究，依据学生发展核心素养体系，结合学科课程的内容，明确学科教学在培育社会主义核心价值观、传承中华民族优秀文化、提高科学素养方面的任务和作用，将德育要求、科学素养培育细化落实到学科课程的教学目标中，是实现学科教学立德育人的首要工作．

(2)要通过学科教学内容的教学，帮助学生了解本学科的概念原理等知识；懂得科学的重要方法；形成科学的思维方式、思维习惯、思维能力和科学的世界观．在此基础上形成能运用学科知识、科学的思维方式和思维习惯解决实际问题的能力．

第二，正确认识和处理学科教学内容三要素基础知识、基本技能、学科方法间的关系．学科基础知识和基本技能是人类在学科领域的认知活动中获得的宝贵成果．是回答学科所研究的客观事物“是什么”“为什么”等具体问题的事实性知识．学科的研究方法，是进行学科研究、解决学科问题过程中为达到预期目的所采取的策略、途径、步骤、规则、手段和方式方法．它回答“怎么研究”“怎么表征”的问题．在知识技能教学中渗透科学方法的教育，帮助学生了解知识的形成过程，了解人们探索自然、社会发展规律的方法，才能领悟习得探究世界的方法，迁移运用所学的知识．

第三，逐步提高自己学科教学育人的意识和能力．身教胜于言教，处处为人师表．严格要求自己，在品德修养、行为作风、治学精神、仪表举止等方面，都应成为学生的榜样，就可以收到“其身正，不令而行”的良好效果．学而不厌，诲人不倦，要通过多种渠道掌握精湛的专业知识和良好的文化修养．

总之，要发挥学科教学的育人功能，有效地提高学生的核心素养，需要充分认识学科教学内容的育人功能，在教学中正确地看待、处理学科教学内容三要素的关系．在此基础上，研究如何依据学科课程标准，明确学科在各学段具体的育人目标、任务和教学内容；根据学生的认知规律和心理发展水平设计和组织学科教学，注重各个学科间的联系，才能发挥学科教学综合育人的功能．