非自治三分量可逆Gray-Scott系统的拉回指数吸引子*1

田永笑， 周盛凡

·数学·

非自治三分量可逆Gray-Scott系统的拉回指数吸引子*1

田永笑， 周盛凡

（浙江师范大学数理与信息工程学院，浙江金华321004）

主要研究用于模拟2个可逆化学反应的非自治三分量可逆Gray-Scott系统的初边值问题的拉回指数吸引子的存在性问题.当非自治外力项在局部可积函数空间里平移有界时，首先介绍了该系统的解的存在唯一性；其次证明了该系统的解在相空间与稍高正则空间中的最终一致有界性；然后证明了系统的解在一簇正不变闭子集上满足Lipschitz连续性，同时对两解之差进行“尾估计”；最后利用拉回指数吸引子存在性判据，得到了该系统拉回指数吸引子的存在性，并且得到拉回指数吸引子分形维数的上界及吸引有界集的指数率估计式.

非自治；拉回指数吸引子；可逆的Gray-Scott系统；分形维数

0　引言

考虑非自治三分量可逆的Gray-Scott系统的初边值问题：

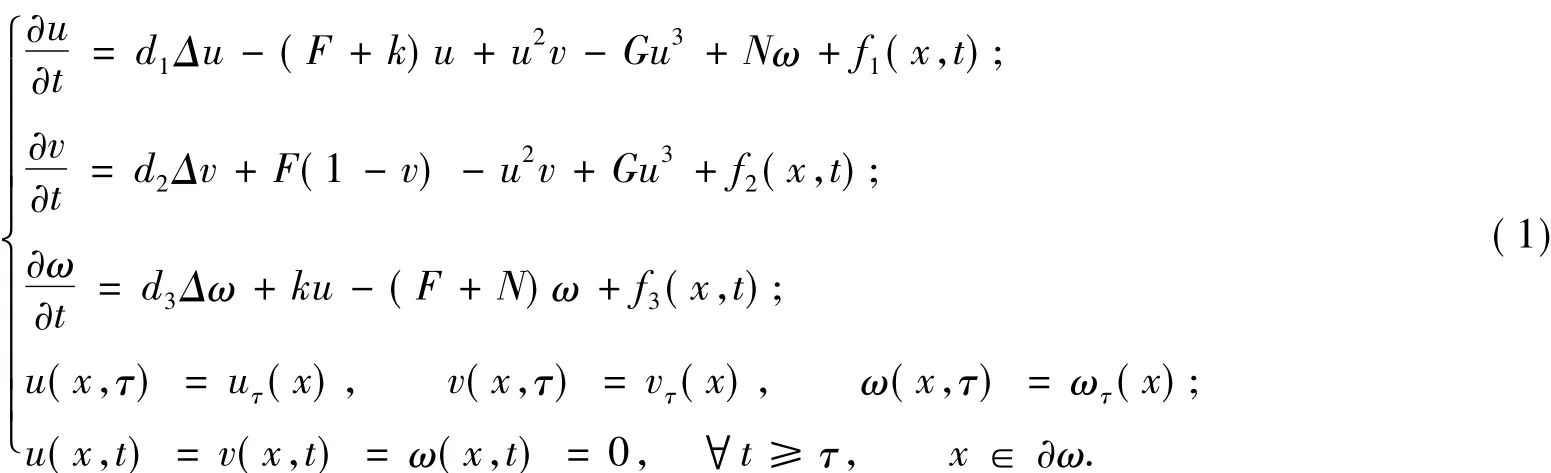
式（1）中：u（x，t），v（x，t），ω（x，t）是Ω×（τ，+∞）上的实值函数；τ∈R；Ω⊂Rn（n≤3）是具有光滑边界∂Ω的有界区域；d1，d2，d3，F，k是正数；G和N是非负数；fi（·，t）∈L2loc（R；L2（Ω））是平移有界的，i= 1，2，3，即

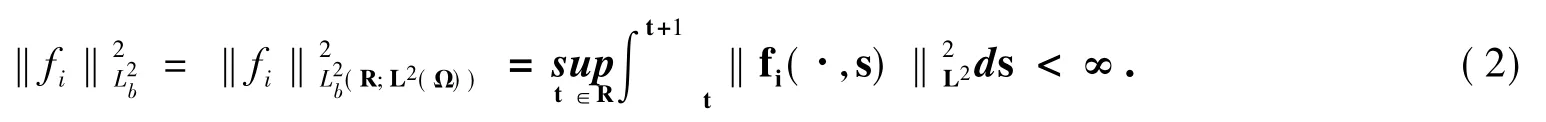
三分量可逆的Gray-Scott系统（1）最初由Mahara等［1］提出，用于模拟2个可逆化学或生化反应问题，后由You［2］经无量纲化得到.对于自治的三分量可逆的Gray-Scott系统，即非自治项fi（i=1，2，3）与时间t无关，You在文献［2］和文献［3］中分别证明了它的整体吸引子的存在性及其鲁棒性.对于非自治系统（1），Gu等证明了其一致吸引子的存在性［4］和拉回吸引子的存在性［5］.整体吸引子、一致吸引子和拉回吸引子吸引轨道或有界集的速度有时可能很慢且其维数不一定有界，这给实际应用及模拟带来困难.为此，对于非自治系统，有关学者［6-12］提出了拉回指数吸引子的概念并已应用于实际系统.拉回指数吸引子是一簇正不变的具有有限维数的紧集且指数吸引相空间的所有有界集，同时包含相应的拉回吸引子.到目前为止，关于系统（1）的拉回指数吸引子尚无任何结果.本文利用文献［7］的方法，证明系统（1）存在拉回指数吸引子，并由此可知文献［2-5］中的整体吸引子和拉回吸引子都有有限的维数且最终一致指数吸引相空间的有界集，从而推广了已有的结果.

1　解的存在唯一　性

令

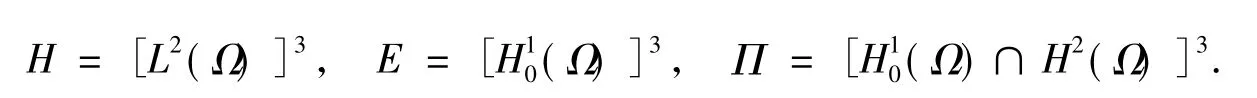
用‖·‖和〈·，·〉表示H或L2（Ω）的范数和内积，‖·‖Lp（p≠2）表示Lp（Ω）或［Lp（Ω）］3的范数.取‖▽ξ‖作为‖ξ‖E或‖ξ‖H10（Ω）范数，|·|表示Lebesgue测度或绝对值.

由Lumer-Phillips定理可知，线性算子

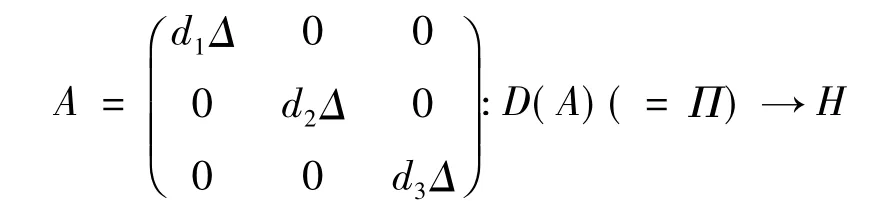
生成Hilbert空间H上的解析半群.通过嵌入定理和Hölder不等式知，

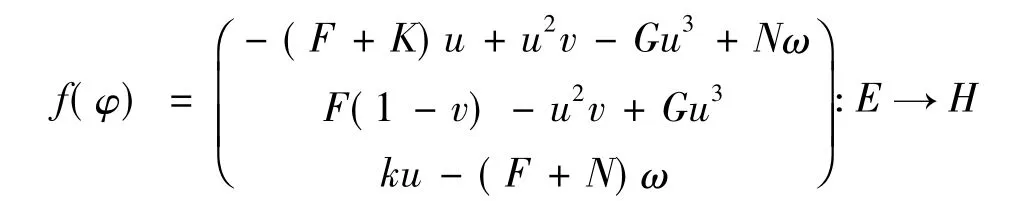
是局部Lipschitz连续的映射，其中φ=（u，v，ω）T.

定理1对任意给定的τ∈R和初值φ（τ）=（u（τ），v（τ），ω（τ））T∈H，问题（1）存在唯一弱解φ（t）=φ（t，τ；φτ）=（u（t），v（t），ω（t））T，满足φ（τ，τ；φτ）=φτ，φ（·，τ；φτ）∈C（［τ，∞）；H）∩L2loc（［τ，∞）；E）和φ（t，τ；φτ）关于φτ∈H连续，并且映射簇U（t，τ）：φτ=（u（τ），v（τ），ω（τ））T∈H|→φ（t，τ；φτ）=（u（t，τ），v（t，τ），ω（t，τ））T∈H，t≥τ，τ∈R，构成H上一个连续算子过程｛U（t，τ）｝t≥τ.

证明证明类似于文献［4］中的引理2.1，故略.

2　拉回指数吸引子的存在性

首先证明系统（1）的解的最终一致有界性，即有下面引理：

引理1过程｛U（t，τ）｝t≥τ在H中存在一致有界闭的吸收球B0=B（0，r0）=｛φ∈H：‖φ‖≤r0｝⊂H（r0与τ，t无关），即对于τ∈R及任意的有界子集B⊂H，存在TB≥0，使得当t≥TB时，U（t+τ，τ）B⊆B0.

取内积〈式（3），Gu（t）〉，〈式（4），v（t）〉，〈式（5），GW（t）〉，相加并整理得

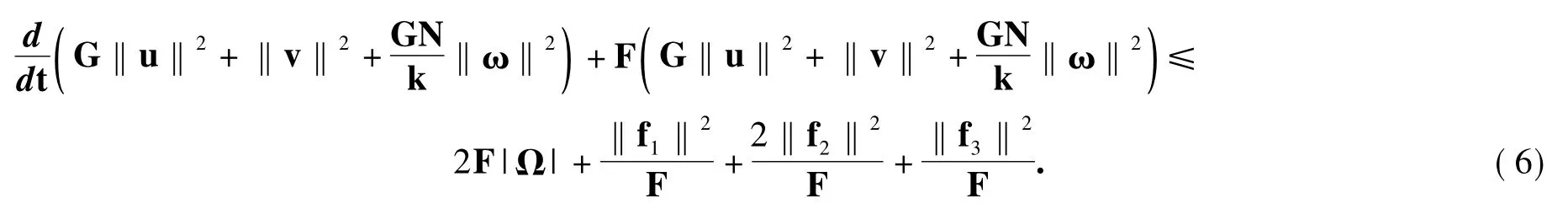
在［τ，t+τ］上对式（6）应用Gronwall不等式，由式（2）得

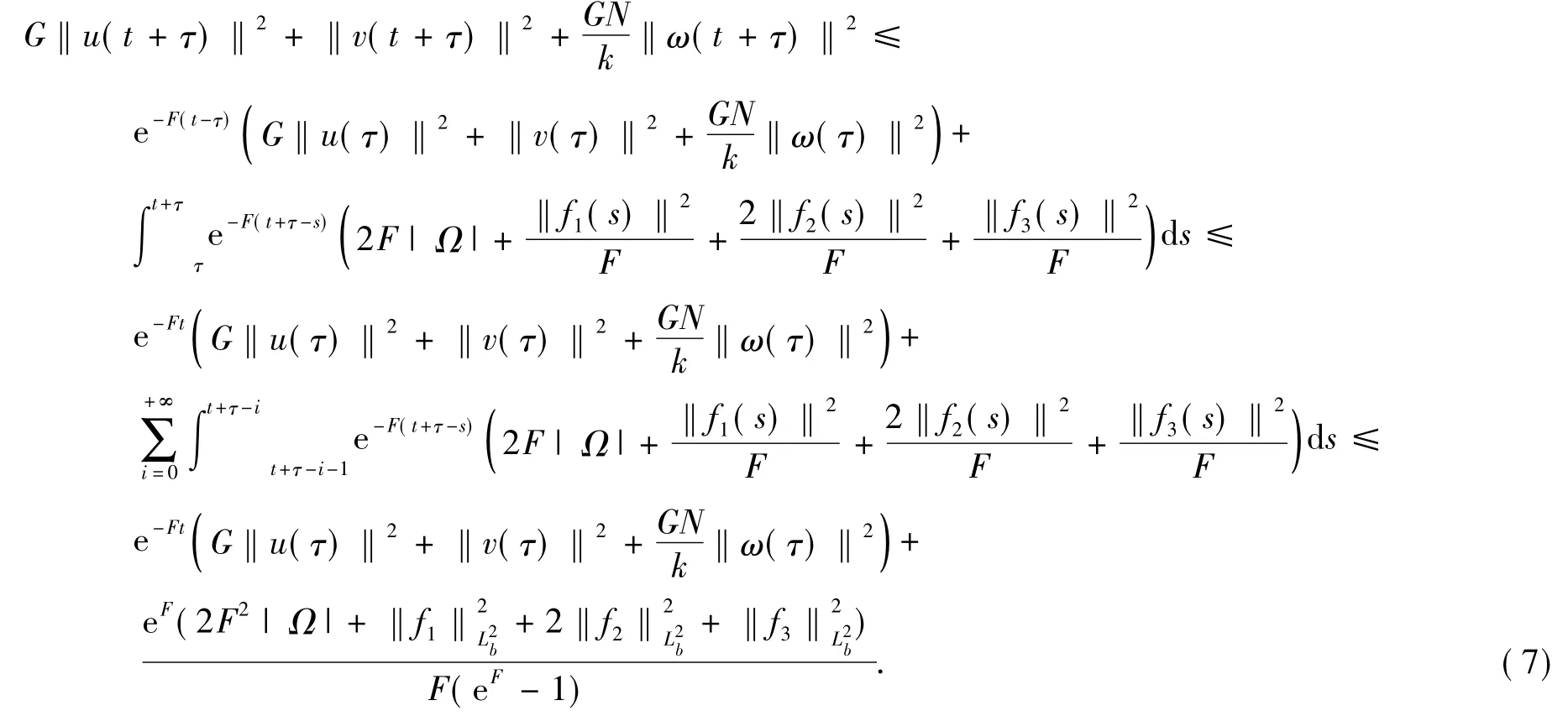
其次考虑系统（1）的解的最终正则性，有下面引理：

引理2存在正数r1＞0及，使得对任意φτ∈B0，当t≥TB0+1时，有‖U（t+τ，τ）φτ‖E≤r1.

证明取内积〈式（1），（-Δu，-Δv，-Δω）T〉得

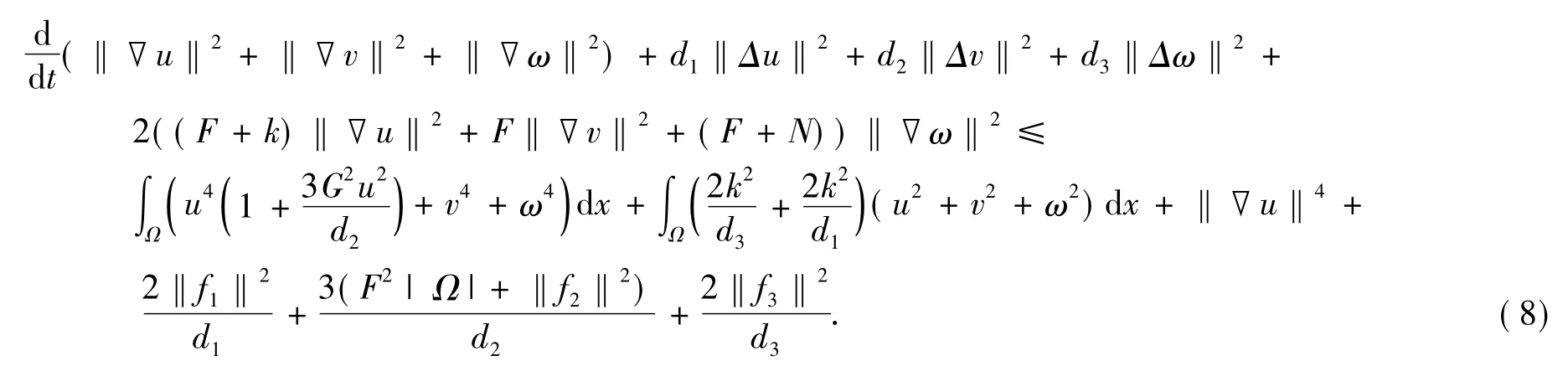
根据Sobolev嵌入不等式知，存在正数b3，使得对于所有φ∈E，有‖φ‖L4≤b3‖φ‖E=b3‖▽φ‖.于是，对t≥TB0，由式（8）得

由式（6）知，对t≥TB0，有

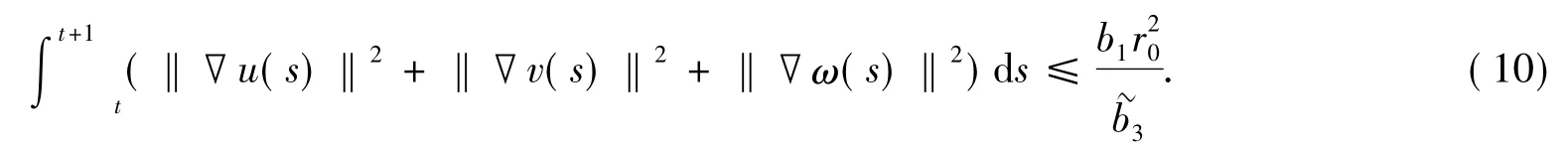
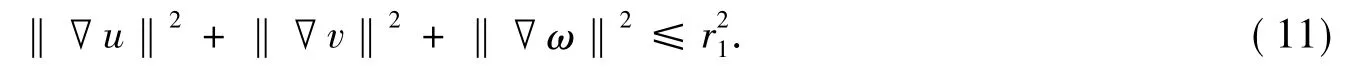
对任意的t∈R，令

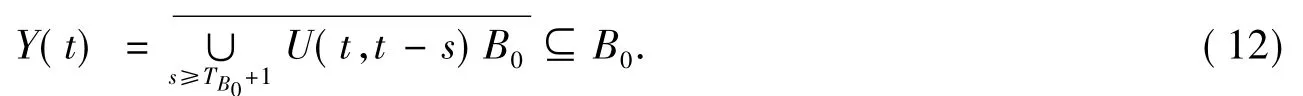
式（12）中，B0是引理1中的一致吸收球.令B1=｛φ∈E：‖φ‖E≤r1｝，则

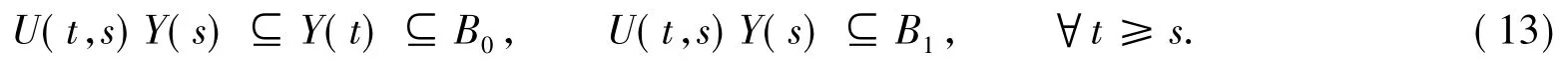
现在考虑算子过程｛U（t，τ）｝t≥τ在｛Y（τ）｝τ∈R上的Lipschitz连续性.对每一个τ∈R和φjτ∈Y （τ），j=1，2，令

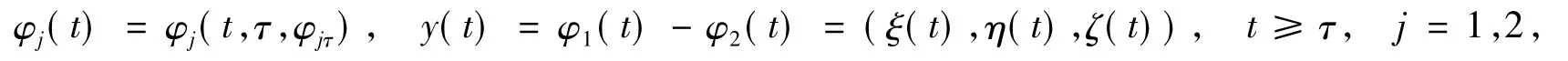
则

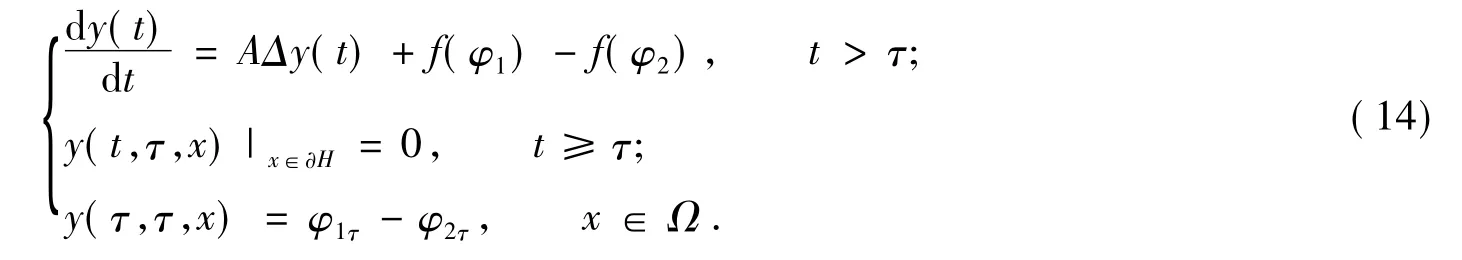
式（14）中，

谁都知道老虎有吃人的凶残本性，然而不受任何约束或限制的权力，与老虎比较而言，可谓“有过之而无不及”。权力究竟为何物?尽管人们有许多不同的理解或释义，但谁都知道它是一种“力”，一种不同寻常的“力”。同其他“力”(自然力)相比较，权力的独特之处突出表现在两个方面:一是作用领域的广泛性，二是能量膨胀的自发性。

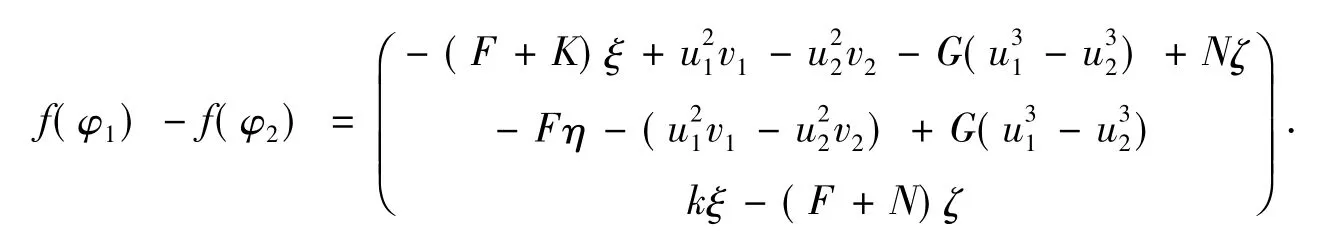
由式（13）和引理2知，对t≥τ，有φ1（t），φ2（t）∈Y（τ）.由式（11）得

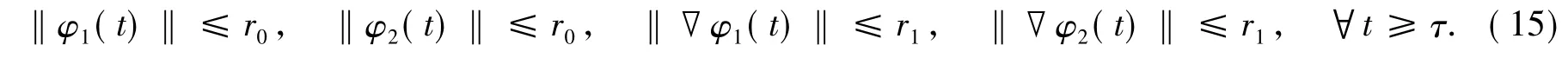
引理3存在一个正值函数L（t），使得对于每一个τ∈R，有

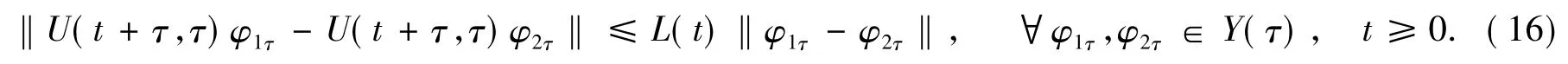
证明用y（t）与式（14）作内积（·，·）H，有

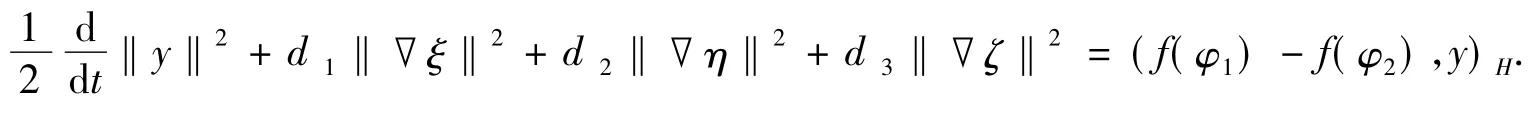
由Sobolev嵌入不等式知，存在正数b4，使得‖φ‖L6≤b4‖φ‖E=b4‖▽φ‖对任意φ∈E都成立，从而

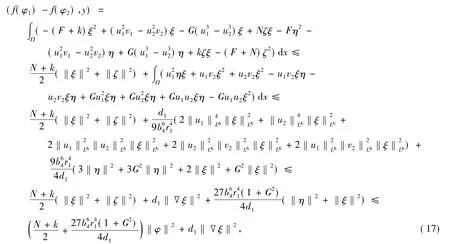
于是

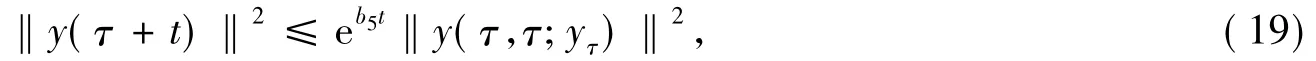
易见，D（-Δ）=H2（Ω）∩H01（Ω），并且算子-Δ具有正的特征值｛λm｝m∈N：

记｛em｝m∈N⊂D（-Δ）是算子-Δ关于特征值｛λm｝m∈N的特征向量，满足-Δem=λmem，m∈N，则｛em｝m∈N是L2（Ω）及的一组正交基.记

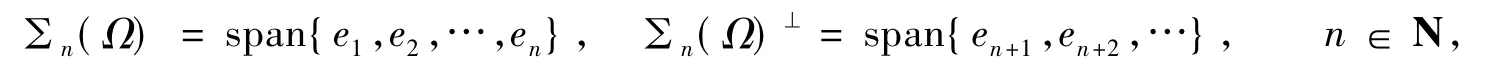
则

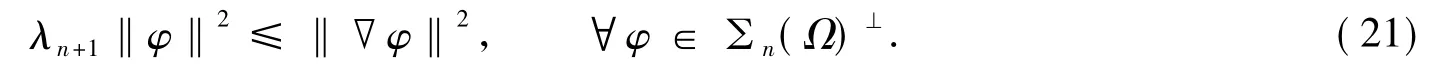
令正交投影

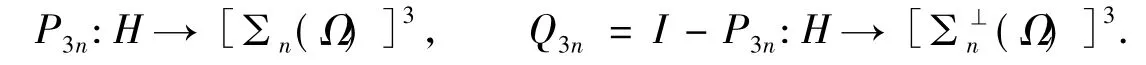
引理4对任意的τ∈R，φ1τ，φ2τ∈Y（τ），存在正数T*＞0)和一个N-维的正交投影P3N：H→［∑N（Ω）］3（N∈Z），使得

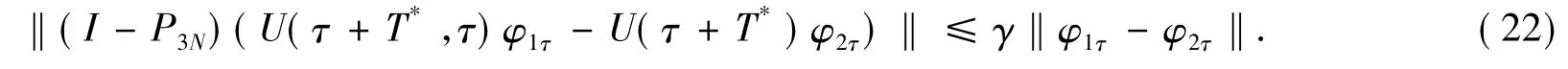
证明在H中让式（14）和y3n=Q3ny作内积，得

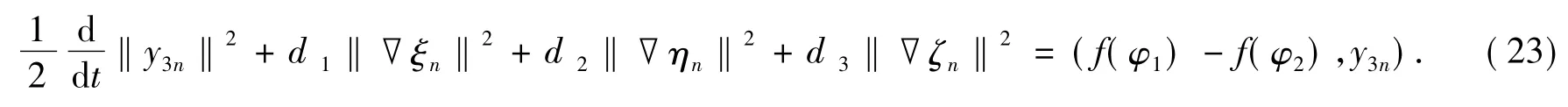
式（23）的右边项为

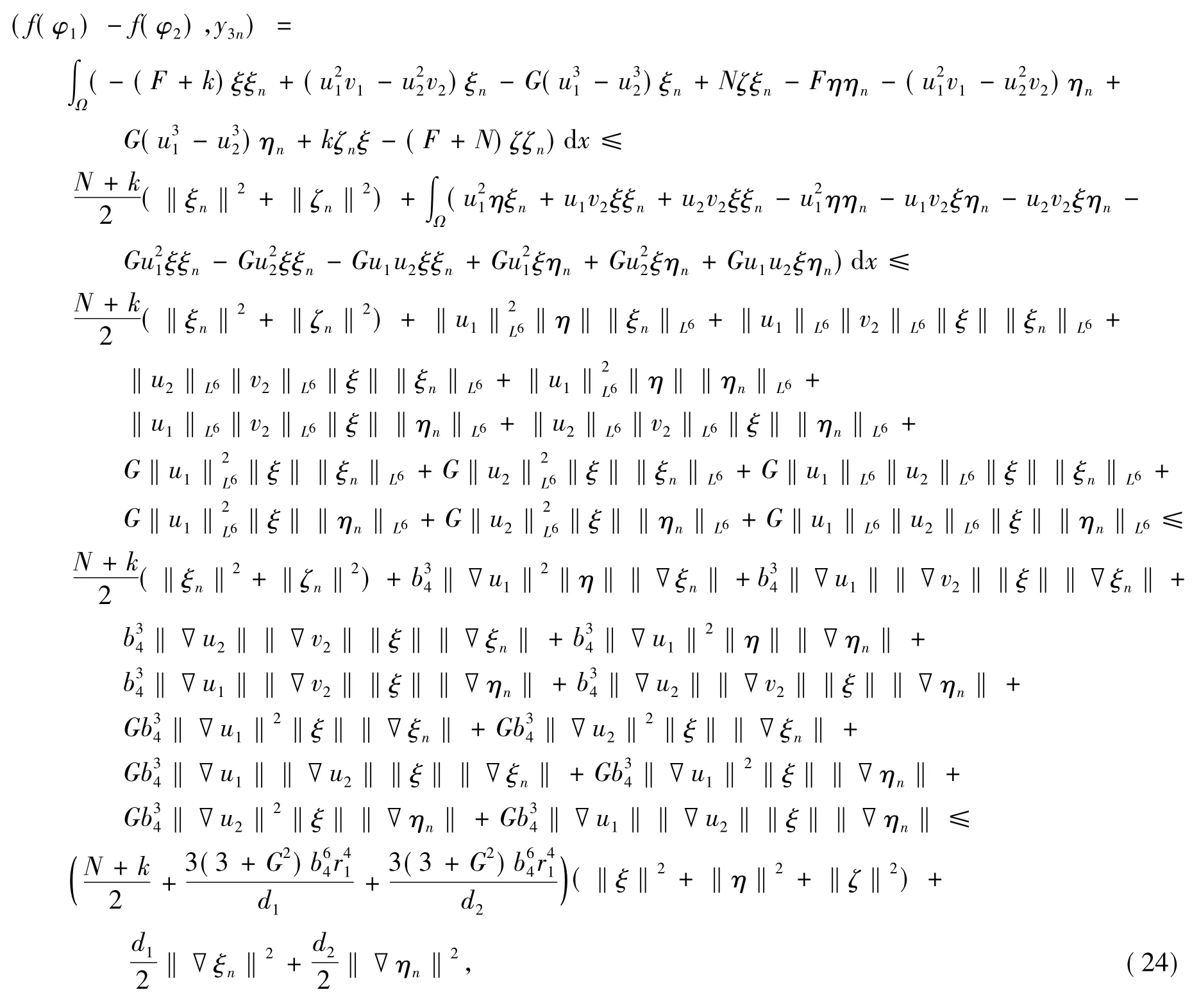
则

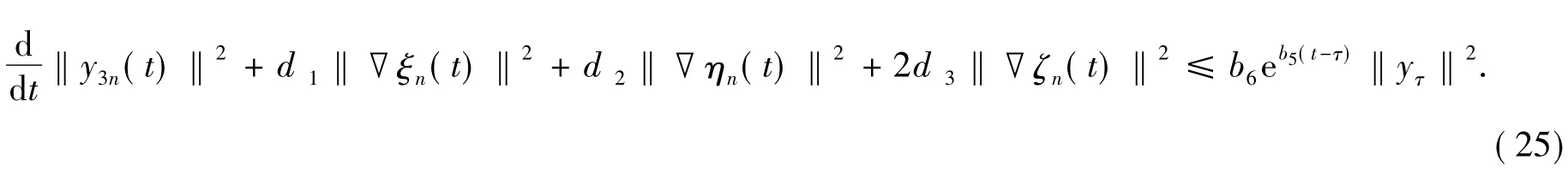
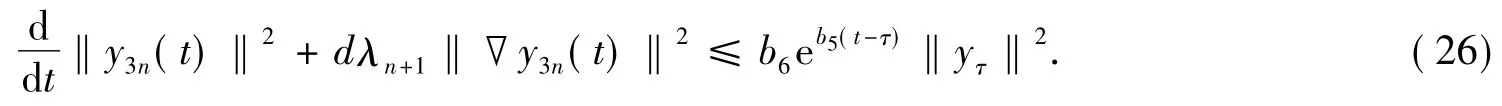
在［τ，τ+t］（t≥0）对式（26）应用Gronwall不等式得

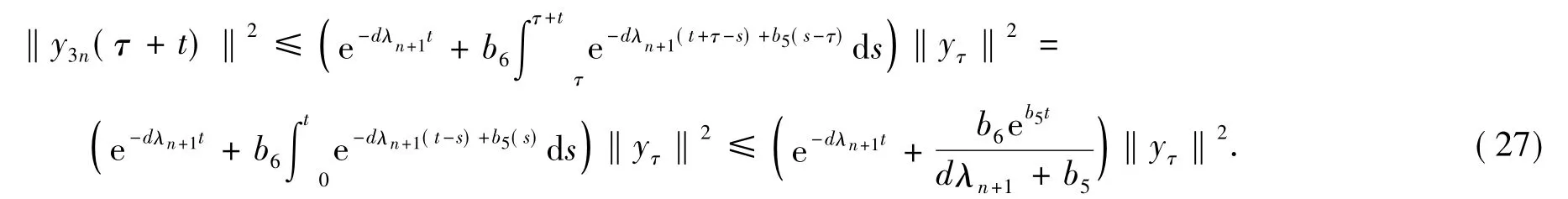
由式（20）知，存在T*＞0及

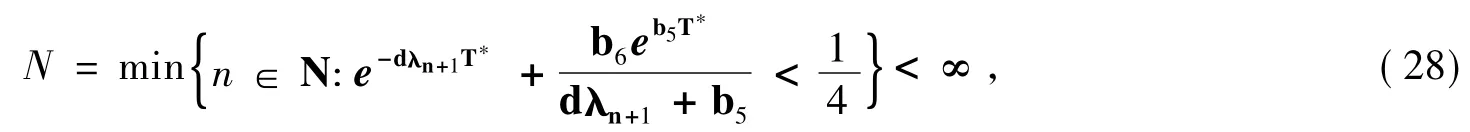
则

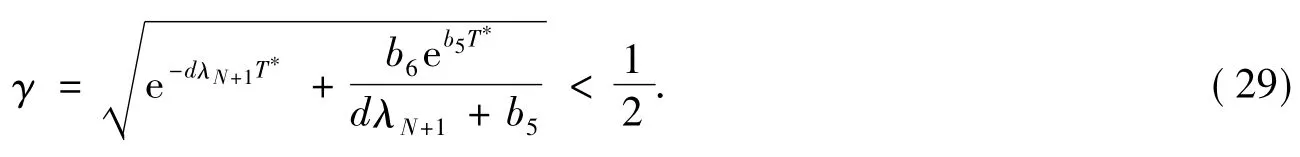
引理4证毕.

证明对任意的τ∈R及初值φτ∈Y（τ），由式（9）得

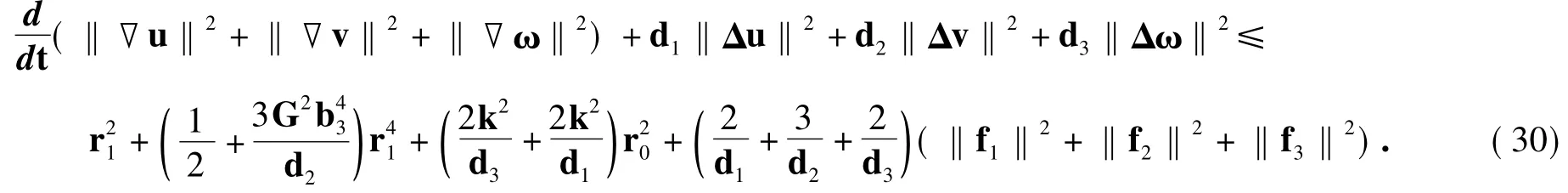
在［τ，t］（t∈［τ，τ+1］）上对其积分，有

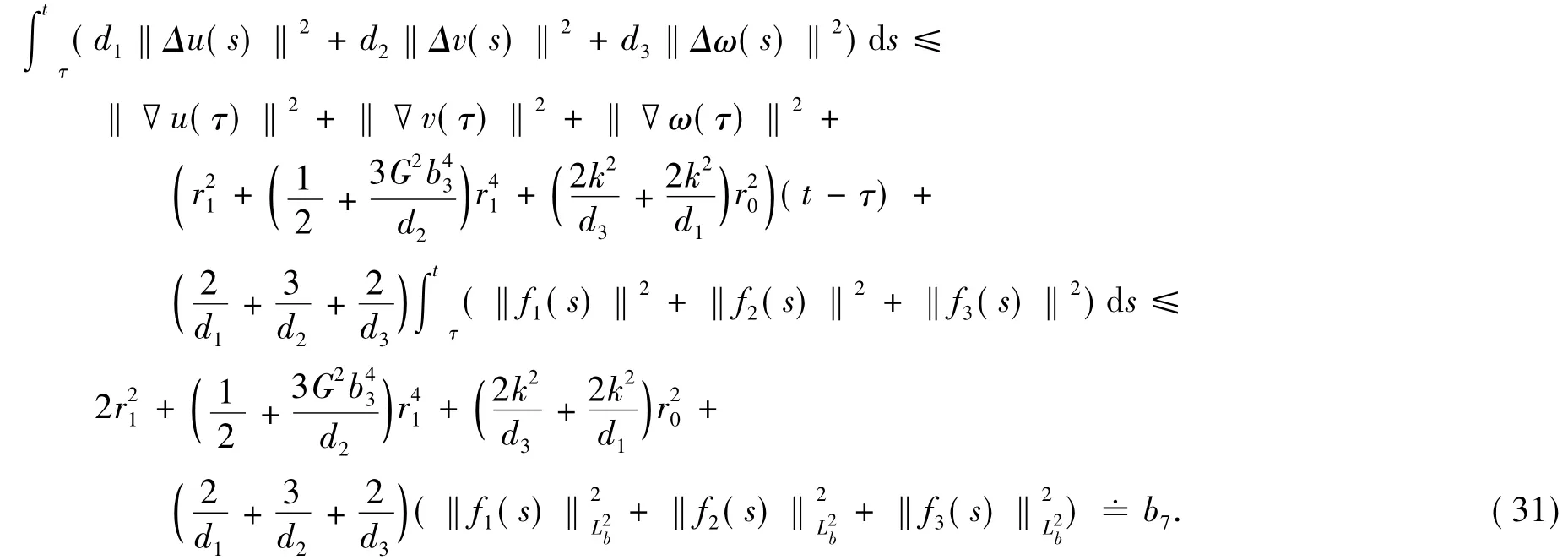
再对方程（1）在［τ，t］（t∈［τ，τ+1］）上积分，得

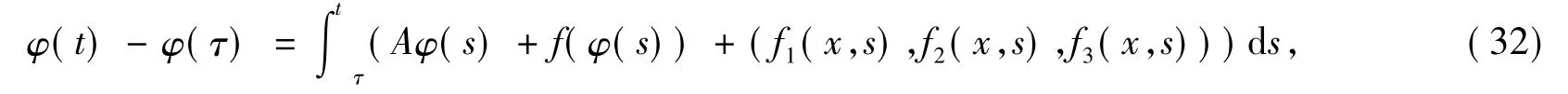
则

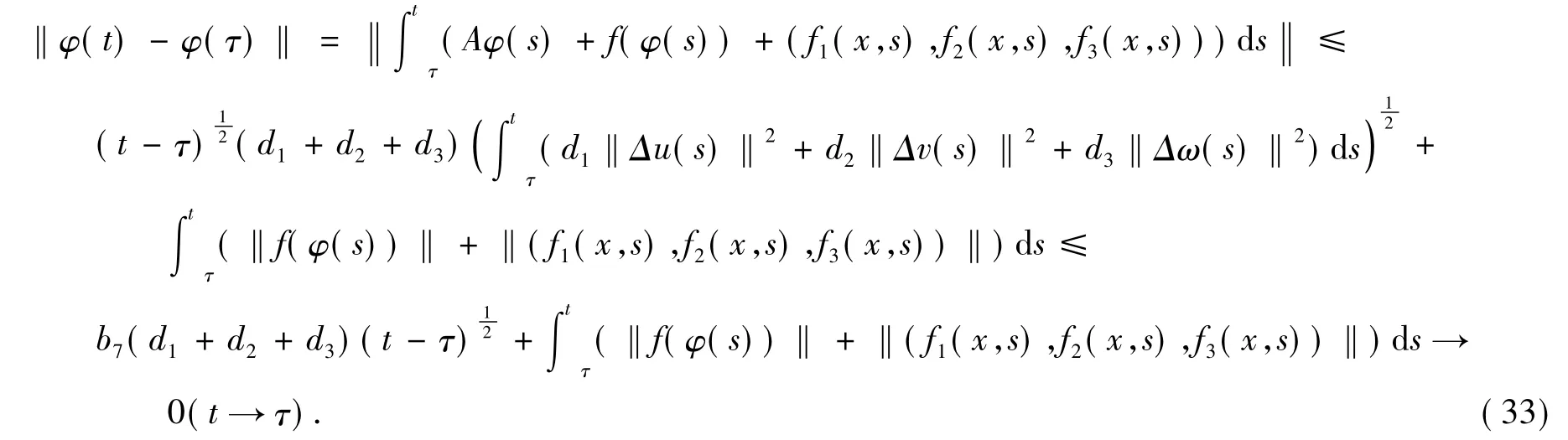
引理5证毕.

根据定理1、引理1—引理5及文献［7］中的定理1，有下面主要结果：

定理2由系统（1）的解确定的过程｛U（t，τ）｝t≥τ在H中有一个拉回指数吸引子｛A（t）｝t∈R，具有以下性质：对任意的τ∈R，

1）K（τ）⊆A（τ）⊆Y（τ）⊆B0；

3　结语

本文主要证明了当依赖时间的外力项在局部可积函数空间里平移有界时，非自治三分量可逆Gray-Scott系统的解过程存在拉回指数吸引子，并且得到拉回指数吸引子的分形维数的上界及吸引有界集的指数率估计式.这些结果可以给可逆Gray-Scott系统在生化反应中的实际应用带来新的思路.

［1］Mahara H，Suematsu N J，Yamaguchi T，et al.Three-variable reversible Gray-Scottmodel［J］.JChem Phys，2004，121（18）：8968-8972.

［2］You Yuncheng.Dynamics of three-component reversible Gray-Scottmodel［J］.Disc Contin Dynam Systems，2010，14（1）：1671-1688.

［3］You Yuncheng.Robustness of global attractors for reversible Gray-Scott systems［J］.JDyn Diff Equat，2012，24（3）：495-520.

［4］Gu Anhui，Zhou Shengfan，Wang Zhaojuan.Uniform attractor of nonautonomous three-component reversible Gray-Scott system［J］.Appl Math Comput，2013，219（16）：8718-8729.

［5］Gu Anhui.Pullback-attractor of nonautonomous three-component reversible Gray-Scott system on unbounded domains［J］.Abstr Appl Anal，2013，2013：719063.

［6］Langa JA，Miranville A，Real J.Pullback exponential attractors［J］.Discret Contin Dynam Syst，2010，26（4）：1329-1357.

［7］Zhou Shengfan，Han Xiaoying.Pullback exponential attractors for nonautonomous Lattice systems［J］.JDyn Diff Equat，2012，24（3）：601-631.

［8］Yan Xingjie，QiWei.Pullback exponential attractors for nonautonomous reaction-diffusion equations［J］.Internat JBifur Chaos Appl SciEngrg，2015，25（5）：35-41.

［9］Li Yongjun，Wang Suyun，Zhao Tinggang.The existence of pullback exponential attractors for nonautonomous dynamical system and applications to nonautonomous reaction diffusion equations［J］.JAppl Anal Comput，2015，5（3）：35-57.

［10］Carvalho A N，Sonner S.Pullback exponential attractors for evolution processes in Banach spaces：properties and applications［J］.Commun Pure Appl Anal，2014，13（3）：1141-1165.

［11］Carvalho A N，Sonner S.Pullback exponential attractors for evolution processes in Banach spaces：theoretical results［J］.Commun Pure Appl Anal，2013，12（6）：3047-3071.

［12］Czaja R，Efendiev M.Pullback exponential attractors for nonautonomous equations Part II：Applications to reaction-diffusion systems［J］.J Math Anal Appl，2011，381（2）：766-780.

（责任编辑陶立方）

Pullback exponential attractors for the non-autonomous three-com ponent reversible Gray-Scott system

TIAN Yongxiao， ZHOU Shengfan
（College of Mathematics，Physicsand Information Engineering，Zhejiang Normal University，Jinhua 321004，China）

Itwas studied the existence of pullback exponential attractor for the nonautonomous three-components reversible Gray-Scott system which was used to simulate two reversible chemical reactions.When the time-depending external forceswere assumed to be translation bounded in the space of locally integrable functions，the existence and uniqueness of solutions for the system could be obtained.The ultimately uniform boundedness of solutions in the state space and amore regular space could be proved also.The Lipschitz continuity of solutions in a family of positive invariant closed subsets could be proved and a"tail estimate"on the difference between two solutions could bemade.The existence of pullback exponential attractor for the system was established by using a criterion concerning the existence of a pullback exponential attractor，moreover，an upper bound of the fractal dimension of this attractor and an estimation of exponentially attracting any bounded setwere also presented.

non-autonomous；pullback exponential attractor；reversible Gray-Scott system；fractal dimension

O175.25

A

1001-5051（2016）02-0121-08

10.16218/j.issn.1001-5051.2016.02.001

*收文日期：2015-09-05；2015-10-17

国家自然科学基金资助项目（11471290）

田永笑（1991-），男，安徽芜湖人，硕士研究生.研究方向：微分方程与动力系统.

周盛凡.E-mail：sfzhou@zjun.cn