基于遗传算法的智能组卷研究

杨刚（安徽职业技术学院信息工程系，安徽合肥230001）



基于遗传算法的智能组卷研究

杨刚
（安徽职业技术学院信息工程系，安徽合肥230001）

计算机技术自问世以来，推动并深化了教育教学改革.在考试环节，可以使用计算机辅助测试系统对学生的学习效果进行测试.计算机辅助测试系统的核心功能是根据约束条件进行组卷.建立了一个改进的组卷数学模型，并使用遗传算法对该模型求解.实验结果表明，该方法能够根据设定的约束条件进行组卷，并且有较高的成功率.

遗传算法；组卷；组卷模型；试卷

在传统考试中，教师要根据教学大纲、考试目的去思考要测验哪些知识点、使用哪些题型、有多少主观题、有多少客观题，然后组织试题形成试卷，这个过程称之为组卷.教师每个学期都要重复这一过程，浪费了时间.在现代教育领域，可以利用计算机辅助测验系统代替人工去完成考试过程中的各种繁杂的重复性工作.计算机辅助测试系统的核心功能是根据约束条件进行组卷［1］，组卷的本质是一个多目标多约束求最优解问题.笔者使用遗传算法进行求解.在编码时，根据试卷的特点采用了分段实数的编码方案，并且在生成初始种群时，就使种群的个体都满足强约束条件.在执行选择操作时，融入了精英保留策略，在执行交叉操作时，采用了分段单点交叉的方式.最后设定了遗传算法的结束条件，获得最优解或已经进化到最大代数.

1组卷的数学模型

设定每道试题具有5个属性，依次是：题号、分值、试题类型、知识点及难度.假设预期试卷的总题数为n，则可以建立一个n*5的矩阵，具体描述如下：

一份试卷需要满足以下几个约束条件：

1）试卷总分约束

式（2）中，S表示试卷的总分数，通常是100分，具体数值有教师根据需求设定.ai2为第i道试题的分值.

2）题型分布约束

3）知识点分数分布约束

式（4）中，M表示所有试卷中所有试题的知识点并集，N表示试卷期望所包含的知识点的并集，以此求得知识点的覆盖率.

4）试卷总体难度约束

式（5）中，S为卷总分.

在本文中把生产试卷的总分表示为S，把试卷的难度值表示为D，把试卷的知识点覆盖率表示为Z，把每种题型的题目数量表示为T.把用户的期望值与实际生成试卷的偏差分别分别表示为DS，DD，DZ，DT，他们的计算公式如下：

式（6）中，S表示生成试卷的总分值，Sp表示期望试卷的总分值，取绝对值表示二者之间的偏差.

式（7）中，D表示生成试卷的难度值，Dp表示期望试卷的难度值，取绝对值表示二者之间的偏差.

式（8）中，Z表示生成试卷的知识点覆盖率，Zp表示期望试卷的知识点覆盖率，取绝对值表示二者之间的偏差.

式（9）中，Tk表示生成试卷的第k种题型的题目数量，Tkp表示期望试卷的第k种题型的题目数量，取绝对值表示二者之间的偏差.

所以组卷的目标函数f可如下表示：

2遗传算法在组卷中的应用

遗传算法是一种启发式随机搜索方法，在搜索的过程中，不断向最优解靠近.遗传算法在执行过程中，模仿自然界生物进化过程中选择和遗传，是一种多参数、多群体同时优化的方法.使用遗传算法进行组卷的过程如下.

步骤1：生成初始种群

生成初始种群是遗传算法的第一步.然后会对初始种群中的个体进行评价，如果初始种群已包含最优解，则直接输出结果，否则进行选择、交叉和变异找出最优解.

把试卷的约束条件分为强约束和弱约束两种.强约束包括试卷的总分值，以及各种题型对应的题目数量.初始种群中的每个个体都是随机产生的，但这种随机是有限制的，即生成的个体必须满足试卷总分值和题型分布这2个强约束条件.

步骤2：编码

应用遗传算法求解问题时，要将问题的解映射成染色体，并采用分段实数编码方式.将一份试卷映射为一个染色体，染色体上的每一个基因就是试卷中的一道试题，基因的值直接用试题的题号表示［2］.比如一份试卷型有4个单选题，4个多选题，3个判断题，2个填空题，2个问答题，它的染色体的编码如图1所示.

图1　染色体编码

步骤3：选取适应度函数

遗传算法在对问题求解的过程中，考察个体的唯一指标就是适应度值.一般而言，适应度值高，则说明个体好，反之说明个体坏，容易被淘汰.所以适应度函数的选取是十分关键的，要能把个体的好坏区分开来［3］.

在生成初始种群时，种群中的个体已经满足了试卷总分值约束和题型分布约束，因此式（10）中的DS=0，DT=0，故组卷的目标函数转变为

通常适应度函数就是目标函数.由公式（11）可知，当f的值趋近于0时，生成的试卷越符合约束条件.但函数取最小值不方便执行后续的选择操作，因此对其做如下变换得到适应度函数：

步骤4：遗传操作

1）选择

采用轮盘赌作为选择算子，但轮盘赌容易发生优良个体丢失的情况.因此，在执行选择的过程中加入了精英保留策略，该策略能够将父代中适应度值最高的个体保留下来.具体的实现步骤是：

①在进化的过程中，对每一进化后产生的子代种群，计算其每个个体的适应度值，并找出最大值.

②将子代种群中的最优个体与父代种群中的最优个体相比，如果父代种群的最优个体的适应度值大，则随机从子代种群中选择一个个体，淘汰该个体后，把父代种群中的最优个体加入种群中；如果子代种群的最大适应度值比较大，则不改变子代种群，继续进行求解.

2）交叉

设定的编码方案是分段实数编码，每种题型即一段，为保证交叉操作不影响题型的分布，设定交叉在段内进行，且同一段内只交叉一个基因，整个染色体就表现为多点交叉［4］.

3）变异

在交叉操作后，对种群中的个体进行评价，如果没有找到最优解，则执行变异操作.把变异算子也改进为在段内进行，且为单点变异.并且在变异操作中加入以下几个约束条件：不能选择重复的试题，新的试题的分值要与原来相同，新的试题的所包含知识点是与原有知识点，或是原有知识点的子集［5］.

交叉的具体过程如下：

①选择种群中的一个个体.

②在个体中各题型对应的段内随机寻找一个基因.

③从题库中抽取一个对应的试题，改变第二步基因位上的值.

步骤5：终止遗传算法

遗传算法的运算过程是一种迭代，如果使用不当，会陷入无线循环中.设置最大进化代数为500，当进化到500代时，如果仍然没有找到最优解，算法将停止运算.

3实验及结果分析

在操作系统Microsoft Windows XP，CPU Intel Core i3 2.4 GHz，2 G内存，C#4.0环境下，编程实现了遗传算法.为了验证算法的可行性和有效性，使用题库《电工电子》进行组卷实验.该题库包含单选题、多选题、判断题、填空题及简答题5种题型，每种题型单题的分值分别为1，2，1，1-4和3-10.该题库的题型数量级难度分布特征如表1所示.

题库中的总知识点为120个，编号从1开始.题库中的每道试题最少包含1个知识点，最多包含4个知识点.

按照表2设置试卷的约束条件.设置初始种群数量为20，选择次数为10次，最大迭代次数为500.设定适应度期望值为0.95，0.96，0.97，0.98，0.99，各组卷500次.

表1　题库《电工电子》的特征

表2　《电工电子》试卷组卷要求

适应度为0.95时组卷500次，成功率为100%.运行结果如表3所示.

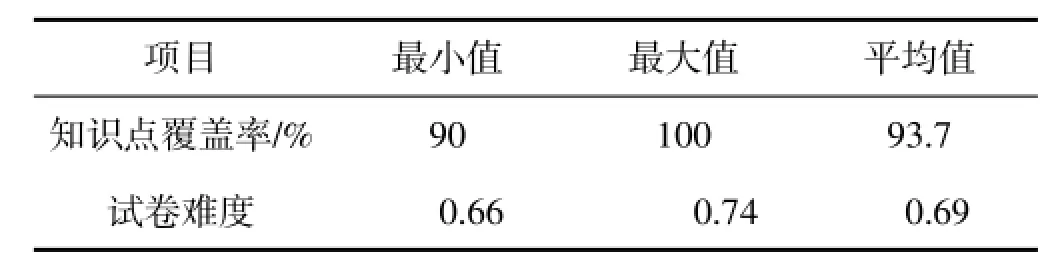
表3　《电工电子》适应度为0.95组卷结果

适应度为0.96时组卷500次，成功率为100%.运行结果如表4所示.

适应度为0.97时组卷500次，成功率为100%.运行结果如表5所示.

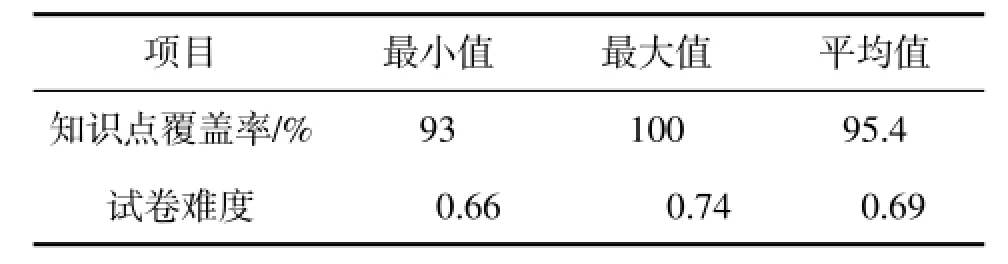
表4　《电工电子》适应度为0.96组卷结果

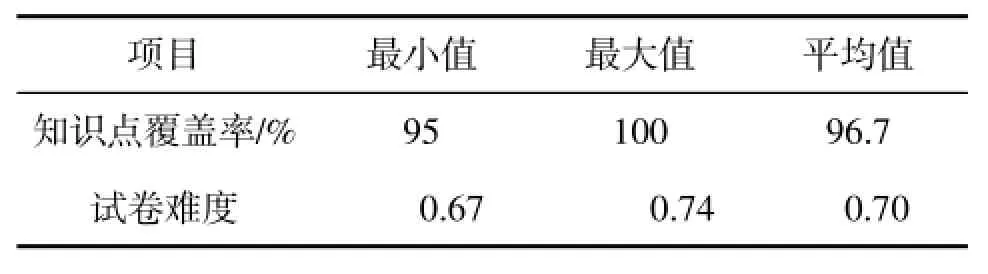
表5　《电工电子》适应度为0.97组卷结果

适应度为0.98时组卷500次，成功率为97.4%.运行结果如表6所示.

适应度为0.99时组卷500次，成功率为93.5%.运行结果如表7所示.

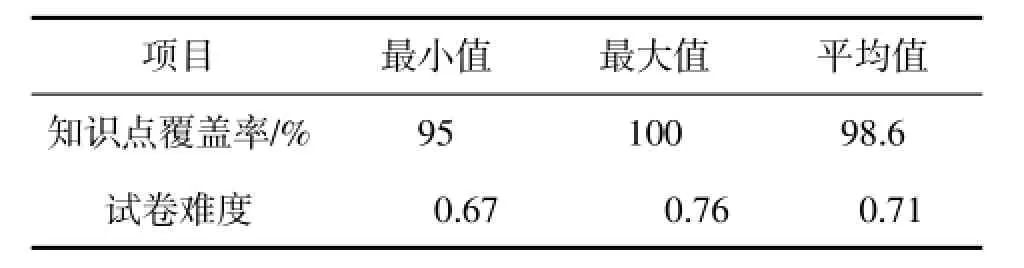
表6　《电工电子》适应度为0.98组卷结果

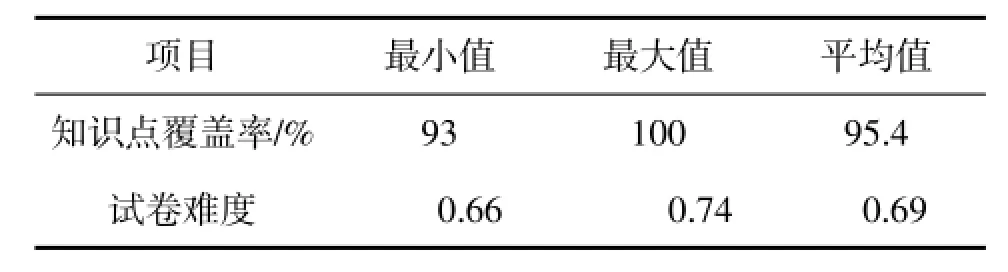
表7　《电工电子》适应度为0.99组卷结果

适应度值从0.95至0.99，所需的平均进化代数如表8所示.

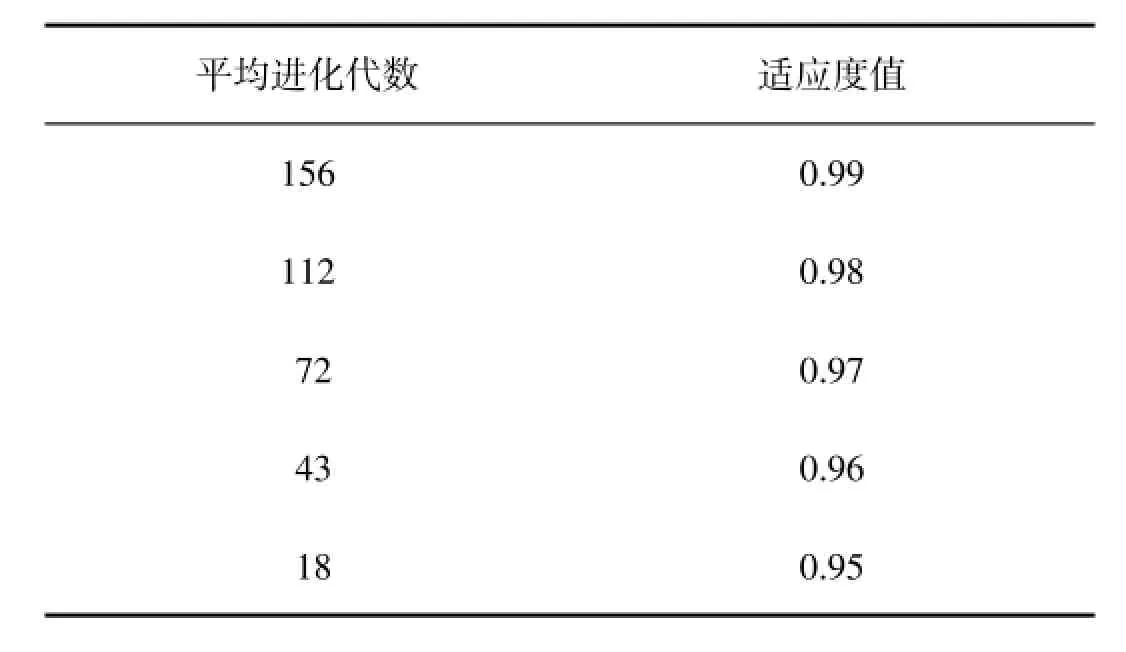
表8　《电工电子》适应度值与平均进化代数

4结论

根据适应度函数，当适应度的值越接近1.0，表明生成的试卷越符合预期要求.本文的实验结果显示，当适应度期望值在0.98以下时，组卷的成功率为100%.当适应度期望值为0.98和0.99时，组卷的成功率在92%以上.已达到预期的要求.

［1］黄光扬，龙文祥.教育测量与评价［M］.上海：华东师范大学出版社，2002

［2］张晋，李冬黎，李平.遗传算法编码机制的比较研究［J］.中国矿业大学学报，2002，（6）：45-48.

［3］李延梅.一种改进的遗传算法及应用［D］.广州：华南理工大学，2012.

［4］贺荣，陈爽.在线组卷策略的研究与设计［J］.计算机工程与设计，2011，（6）：2183-2186.

［5］朱文坚，陈东，刘建素.遗传算法在多目标优化设计中的应用研究［J］.机械工程师，2001，（12）：35-37.

（责任编辑李健飞）

A Research on Intelligent Test Paper Com poser Based on Genetic Algorithm

YANG Gang
（Department of Information Engineering，Anhui Vocational College Technology，Hefei，Anhui 230011，China）

Since computer technology came into being，it has promoted the deepening of educational reform.In the test session，the computer-aided test system is used for testing students'learning effect.This system includes multiple functional modules with its core function of composing test paper based on constraints.In this paper，an imp roved test paper mathematical model is established and genetic algorithm is used to solve the model.The experiment results show that the method can be used to compose test papers based on the fixed constraints，possessing a higher success rate.

genetic algorithm；test paper composer；test paper composer model；test paper

TP39

A

1673-1972（2016）03-0042-05

2016-04-16

2010年安徽省高等教育质量工程教学研究项目（20101512）

杨刚（1982-），男，安徽五河人，讲师，主要从事算法分析与设计、软件工程研究.