改进的DSSS电磁波随钻测量信号载频估计算法

苏　毅，许泽玮，刘　晨（1.中国人民大学商学院，北京10087；.中国石油规划总院，北京10008；.九一金融信息服务（北京）有限公司，北京100888）

改进的DSSS电磁波随钻测量信号载频估计算法

苏毅1，2，许泽玮3，刘晨2
（1.中国人民大学商学院，北京100872；2.中国石油规划总院，北京100083；3.九一金融信息服务（北京）有限公司，北京100888）

为了解决随钻测量中电磁波信号的载频估计问题，基于直接序列扩频（DSSS）通信原理，建立了改进的电磁波信号载频估计法，该方法采用信号自适应干扰对消技术滤除噪声信号，然后再通过带通滤波技术获得DSSS信号的频带，从而提高了信号的信噪比（SNR）。在此基础上，建立了System View仿真模型，仿真结果表明：改进的载频估计法可以有效滤除噪声信号，精确地检测出电磁波信号的载波频率。

直接序列扩频；自适应滤波；载频估计；噪声抑制

0　引言

电磁波随钻测量过程中，钻具工作环境恶劣，如温度变化、噪音、震动、冲击等，这些都会对电磁波信号造成干扰［1］。同时由于不同地区地质条件差异很大，在大地电磁信道模型不变的前提下，利用电磁波进行透地通信时，需要选择最佳的调制与降噪方式，以提高信号的抗干扰性能［2］。直接序列扩频（direct sequence spread spectrum，DSSS），用高速率的伪码序列与信息码序列模2加（波形相乘）后的复合码序列去控制载波的相位而获得DSSS信号，即将原来较高功率、较窄的频率变成具有较宽频的低功率频率，从而可以获得令人满意的抗噪声干扰性能。

本文基于DSSS原理，建立了改进的电磁波信号载频估计法，仿真结果表明算法可以有效滤除噪声信号，精确检出电磁波信号载频。

1　DSSS扩频通信原理

DSSS用一组高速率的伪码序列将要发送的信息码序列扩展到一个很宽的频带上，在接收端利用同一组伪码序列对扩频信号进行解扩处理，从而得到原来的信息［3］。噪声序列与伪码序列不相关，于是在接收端被扩频，从而大大降低了信号频带内噪声信号的功率，提高了系统的信噪比，起到了抗干扰的效果。DSSS系统的工作原理如图1所示。

发射端，二进制信息码a与高速率的伪码序列b进行模2加运算，得到扩频序列c，再经过载波调制，便得到扩频调制的发射信号。接收端，扩频信号x经过高功率放大和混频后，得到中频扩频信号f，再用高速率的伪码序列b对f进行解扩运算，将信号的频带恢复为原信息码序列的频带，即中频调制信号g，然后再经过解调，得到原二进制信息码，完成数据传输。

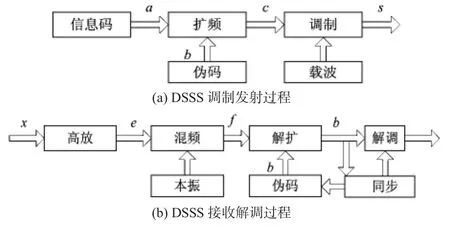
图1　DSSS系统工作原理Fig 1　Working principle of DSSS system

DSSS的信号模型可以表示为［4］

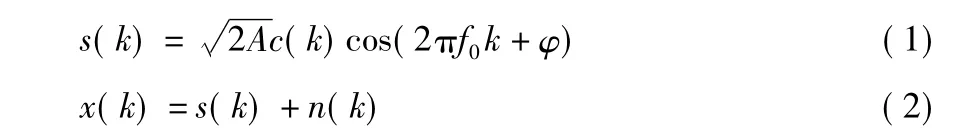
式中A为信号的功率；c（k）∈｛-1，1｝是伪码扩频调制信号；f0为载波频率；φ为在区间（0，2π）内均匀分布的随机变量；s（k）为DSSS信号；n（k）为均值为0，方差为σ2，且与s（k）互相独立的高斯白噪声。

DSSS信号的四阶累积C4x（0，τ，τ）包含的信息量较多［4］，可表示为

由于c（k）∈｛-1，1｝，上式可简化为

由式（4）可知，C4s（0，τ，τ）的2-D切片包含了2倍频成分，因此，DSSS信号的载波频率可用它来估计。

2　信号自适应滤波预处理

1）自适应滤波器

对于统计特性随时间变化或未知的输入信号，自适应滤波器通过自动迭代来调整自身参数，以满足信号处理的要求，从而达到最佳滤波处理。自适应滤波器可根据不同的准则，产生不同的滤波算法，但主要有两种最基本的算法［5］：递推最小二乘（RLS）法和最小均方（LMS）误差算法。LMS算法的基本思想是：通过调整滤波器自身的参数，使滤波器的输出和信号期望值之间的均方误差最小，这样便可得到有用信号的最佳估计［6，7］。

2）信号自适应干扰对消原理

通信系统中，当信号很微弱或信号完全淹没在噪声中而无法检测时，可采用自适应干扰对消原理，它能将噪声抑制到用直接滤波难以达到的程度。该原理的基本思想是：将传感器的一个或多个参考输入进行滤波处理，并从包含有用信号和噪声的原始输入中减去，从而使原始信号中的噪声衰减或消除，同时保留了有用信号［8，9］。基于LMS算法的自适应干扰对消原理如图2所示，它有两个输入通道，分别为：主输入通道和参考输入通道，其中主通道为有用信号和噪声，参考通道为仅与噪声相关的噪声信号。

图2　自适应干扰对消原理框图Fig 2　Block diagram of adaptive interference cancellation principle

主通道的输入可以表示为

式中n（k）为噪声信号；s（k）为有用的DSSS信号。参考通道的输入n1（k）与n（k）相关，但与s（k）不相关。

系统的代价函数可表示为

由于噪声与有用信号不相关，式（6）可简化为

参考输入信号n1（k）经过FIR滤波器滤波后，产生与噪声n（k）相应的估计输出y（k），原信号减去y（k）便得到系统的输出信号。当代价函数最小时，系统的输出为最优输出，即噪声被滤除到最小。由图2可知，s（k）没有经过自适应滤波器的通道，所以式（7）可表示为

即均方误差E［（n（k）-y（k））2］最小时，y（k）最接近主通道噪声分量n（k），从而可使原信号中的噪声减到最小。

3　改进的载频估计法

载频估计方法原理如图3所示。载频估计的过程为：首先，含有噪声的DSSS信号s（k）经过自适应干扰对消滤波器滤除一部分噪声，得到信号的最佳估计e（k），e（k）再经过带通滤波器滤除其中不含DSSS信号的频带，从而使信号的信噪比得到提高。然后，再经过四阶累积量2-D切片，得到信号s1（k），s1（k）中的噪声远小于x（k）中的噪声。s1（k）中包含了DSSS信号的2倍载频，s1（k）再经过带通滤波器滤除2倍载频以外的频带，通过FFT便可得到DSSS信号的2倍载频，亦即得到DSSS信号的载频。

图3　改进的载频估计法原理框图Fig 3　Principle block diagram of improved carrier frequency estimation method

图3中两个带通滤波器带宽的设置对载波频率的正确估计有很大影响。第一个带通滤波器主要用来滤除不含DSSS信号的频带，它的带宽理论上应设为伪码速率的2倍，同时，还应包含信号的载波频率。第二个滤波器主要用来检测载波的2倍载频，其带宽为滤波器1带宽上下限的2倍。频域上一旦检测出峰值，便可确定载波的2倍载频，亦即确定了信号的载频。

自适应干扰对消滤波器的输出为

式中y（k）=^n（k），为n（k）的最佳估计；n'（k）=n（k）-^n（k），理论上趋于0，即e（k）为DSSS信号的最优估计。

信号经过四阶累积量2-D切片后的输出s1（k）可以表示为

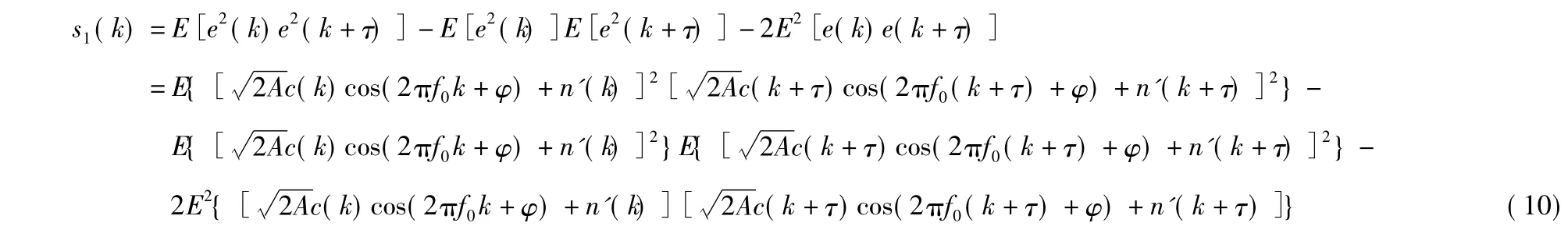
将式（9）代入式（10）便可得到经过四阶累积量滤波后的信号s1（k），通过FFT便可得到DSSS信号的2倍载频，亦即得到DSSS信号的载频。

4　DSSS/FSK仿真分析

利用System View软件进行仿真，建立的DSSS/FSK自适应干扰对消器模型如图4所示。模型参数分别为：滤波器阶数：N=20；PN码序列长度：1023；伪码速率：300 kB/s；信息码速率：300 bit/s；载波频率：120 kHz；调制方式：FSK；带宽：600 kHz。SNR=0 dB时，信号载频估计如图5所示；SNR=-20 dB时，采用改进的载频估计法信号载频估计如图6所示；SNR=-20 dB时，未采用改进的载频估计法的信号载频估计如图7所示。

图4　DSSS/FSK自适应干扰对消器模型Fig 4　DSSS/FSK model for adaptive interference cancellation

可知，图6在240 kHz处明显地有一个峰值，此即DSSS信号的2倍载频；同时图7中可以清楚地看到载波信号被淹没在噪声中，很难被检测出来。可见，采用改进的载频估计法可以滤除噪声信号，精确地检测出电磁波信号的载波频率。

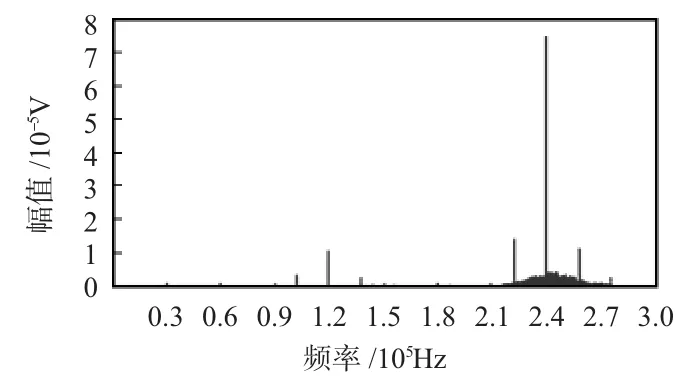
图5　SNR=0 dB载频估计Fig 5　Carrier frequency estimation（SNR=0 dB）

图6　SNR=-20 dB未改进和改进的载频估计Fig 6　Carrier frequency estimation with and without improvement（SNR=-20 dB）

5　结论

采用信号自适应干扰对消技术滤除噪声信号，然后再

通过带通滤波技术获得DSSS信号的频带，从而提高了信号的SNR。为了进一步分析改进的载频估计法的噪声抑制效果，建立了System View仿真模型，仿真结果表明：在电磁波信号被噪声信号淹没的情况下，采用改进的载频估计法可以有效地滤除噪声信号，精确地检测出电磁波信号的载波频率。

［1］李红涛，李皋，孟英峰，等.充气钻井随钻测量脉冲信号衰减规律［J］.石油勘探与开发，2012，39（2）：233-237.

［2］张煜，裘正定，熊轲，等.基于差分脉码调制的随钻测量数据压缩编码算法［J］.石油勘探与开发，2010，37（6）：748-755.

［3］杨阳.DSSS/BPSK及DS/CDMA信号参数估计方法的研究［D］.西安：西安电子科技大学，2014.

［4］沈振惠，唐斌，吕燕，等.基于四阶统计2D切片的直扩信号多参数估计［J］.信号处理，2005，21（3）：304-306.

［5］孟小猛.自适应滤波算法研究及应用［D］.北京：北京邮电大学，2010.

［6］张中华，张端金.一种新的变步长LMS自适应滤波算法及性能分析［J］.系统工程与电子技术，2009，31（9）：2238-2241.

［7］张红梅，韩万刚.一种新的变步长LMS自适应滤波算法研究及其应用［J］.仪器仪表学报，2015，36（8）：1822-1830.

［8］李红.一种变步长符号梯度脉冲噪声对消算法［J］.重庆邮电大学学报：自然科学版，2014，26（5）：654-658.

［9］崔大鹏，行小帅，李竹，等.一种改进的LMS算法及其在噪声对消中的应用［J］.计算机应用与软件，2011，28（3）：128-129.

Signal carrier frequency estimation algorithm for electromagnetic wave measurement while drilling based on improved DSSS

SU Yi1，2，XU Ze-wei3，LIU Chen2
（1.School of Business，Renmin University of China，Beijing 100872，China；2.Petrochina Planning and Engineering Institute，Beijing 100083，China；3.91 Financial Information Service（Beijing）Co Ltd，Beijing 100888，China）

In order to solve problem of carrier frequency estimation of electromagnetic wave signal in measurement while drilling，an improved carrier frequency estimation method is established based on direct sequence spread spectrum（DSSS）.This method adopts adaptive interference cancellation technique to eliminate signal noise. Then，the frequency band of the DSSS signal is obtained through band-pass filtering，so then signal noise ratio （SNR）is improved.On this basis，System View simulation model is established.Simulation results show that the improved DSSS can effectively eliminate noise signal and accurately detect carrier frequency of electromagnetic wave signal.

direct sequence spread spectrum（DSSS）；adaptive filtering；carrier frequency estimation；noise suppression

TP212.9

A

1000—9787（2016）06—0117—03

10.13873/J.1000—9787（2016）06—0117—03

2016—04—11

苏毅（1983-），男，甘肃天水人，中国人民大学商学院博士后，工程师，主要从事机电控制、通信系统数学建模、数值分析等方面的研究。