基于同底三角形面积描述的形状检索
2016-09-02胡大盟黄伟国杨剑宇朱忠奎
胡大盟,黄伟国,杨剑宇,朱忠奎
(苏州大学城市轨道交通学院,江苏苏州 215131)
基于同底三角形面积描述的形状检索
胡大盟,黄伟国,杨剑宇,朱忠奎
(苏州大学城市轨道交通学院,江苏苏州 215131)
为了在形状匹配的过程中提高形状特征对边界噪声和图像变形的鲁棒性,同时兼顾形状匹配算法的检索精度和运算效率,提出一种基于同底三角形面积的形状匹配方法.该方法首先计算每个轮廓采样点的同底三角形面积描述子,并对该描述子进行局部平滑,使其更加鲁棒.然后采用加权L1度量方法计算两个形状所有轮廓点的同底三角形描述子之间的距离,获得匹配代价矩阵.最后利用动态规划算法计算匹配代价矩阵的相似度,获得形状距离,实现形状匹配.通过在MPEG-7、Kimia以及铰接形状数据库上测试分析表明,该方法对变形目标具有良好的鲁棒性,且提高了运算效率和检索精度.
同底三角形;局部平滑;动态规划;混合检索;形状匹配
1 引言
随着数字化多媒体信息技术的快速发展,形状检索成为了机器视觉领域中研究的热点.与物体的纹理、颜色等特征相比,形状特征是一种更高级的视觉信息,识别的鲁棒性和稳定性更高.形状检索的关键在于能否构造出形状特征信息丰富的描述子,而形状的轮廓包含了大量的形状信息,因此国内外研究机构和学者们基于形状的轮廓构造出不同的具有变换不变性的特征描述子,并将这些描述子广泛应用于图像及视频匹配、目标识别、机器人导航、场景分类以及图像分割等计算机视觉领域[1].
基于轮廓边界点的空间位置关系的形状描述方法是近年来最为重要的方法[2].BelongieS等[3]提出了形状上下文(ShapeContexts,SC)描述方法,该方法对目标轮廓的描述能力强,但存在抑制噪声能力较弱,算法复杂度高等问题.LingHB等[4]在SC的基础上提出了内距离形状上下文(Inner-DistanceShapeContext,IDSC),该方法用轮廓点之间的内距离代替SC中的轮廓点之间的欧氏距离.该方法对非刚性铰接物体具有较好的描述效果,但对具有复杂类内信息的目标识别精度不高,且算法复杂度较高.郑丹晨等[5]基于SC提出了一种利用角点典型形状上下文特征(CornerRepresentativeShapeContext,CRSC)进行快速识别的方法,该方法能够降低特征点的匹配时间,有利于解决大规模形状样本的匹配问题,但该方法检索精度不高;GrigorescuC等[6]同样利用轮廓点的空间位置分布关系提出了距离集(Distancesets)的局部描述子,该方法能够较好的获得形状的局部特征,然而忽略了全局特征,特征描述不完整导致形状检索精度较低.
近年来还出现了利用更加稳定的三点空间位置关系来对形状进行特征描述的方法.ElRube等[7]提出了多尺度三角形面积表示方法(Multi-scaleTriangle-areaRepresentation,MTAR),该方法具有较好的抗噪性,但要对形状进行小波分解,计算量较大.AlajlanN等[8]利用轮廓点构成的三角形面积(Triangle-areaRepresentation,TAR)来描述形状,并通过控制三角形的边长来获得形状的多尺度信息,该方法能够有效获得形状的局部和全局特征,但是该算法需要不断改变边长,特征提取较为复杂,且对变形点较为敏感.TemlyakovA等[9]利用德劳内三角化方法对形状轮廓进行分解,并通过定义特征三角形(FeatureTriangle)和叶子三角形(LeafTriangle)来对形状内部的小三角形进行分类.该方法具有较好的形状变换不变性,但是计算复杂度较高.王斌[10]提出了一种多尺度拱高(Multi-ScaleArcHeight,MSAH)形状描述方法,该方法用多尺度的拱高函数来度量形状轮廓线上点的弯曲程度.该算法复杂度较低,但在形状数据库上的检索率不高.
此外,为了进一步提高形状描述子的检索率,一些学者提出了度量学习算法,这些算法能够解决形状距离矩阵中存在不满足三角不等式的问题.如Bai等[11]提出的协同传导(Co-transduction)的形状检索方法,Yang等[12]提出的稠密化距离空间(DensifyingDistanceSpaces)的形状检索方法.这些算法通过获得显著的检索路径,进一步提高描述子的检索精度.
针对现有形状轮廓特征描述方法存在特征描述不完整,且形状特征获取复杂度较高,抗噪能力一般的问题,本文基于轮廓点的空间位置关系提出一种同底三角形面积的形状描述方法.另外,为了提高描述方法的形状检索精度,本文还提出一种混合检索方.本文提出的形状描述方法在抗噪声干扰、运算效率以及匹配精度等方面的表现良好.
2 同底三角形面积表示


(1)

Si={si,u},(u=i,i+1,…,n,1,2…,i-1)
(2)
将式(2)中的CBTA描述子写成n维列向量形式:Si=(si,i,…,si,n,si,1,si,2,…,si,i-1)T,则可用n×n的矩阵{Si}(i=1,…,n)来描述整个形状的特征.图2(b)、(c)、(d)是蝴蝶形状-1的轮廓上不同采样点的CBTA描述子曲线,由图可知采样点在轮廓上所处位置的不同,其对应的CBTA描述子曲线也不同,这表明CBTA描述方法能区分出同一形状中不同轮廓点的相对位置关系.而在同一类形状中相似位置处的点的CBTA描述子向量的曲线的走势基本一致,如蝴蝶形状-1中点A的CBTA曲线与蝴蝶形状-2中点A'的CBTA曲线具有较高的相似性(图2(b)和图3(b)).以上分析表明CBTA描述子不仅具有较好的区分轮廓采样点位置的能力,还具有对同类形状的相似位置处点的聚类能力.

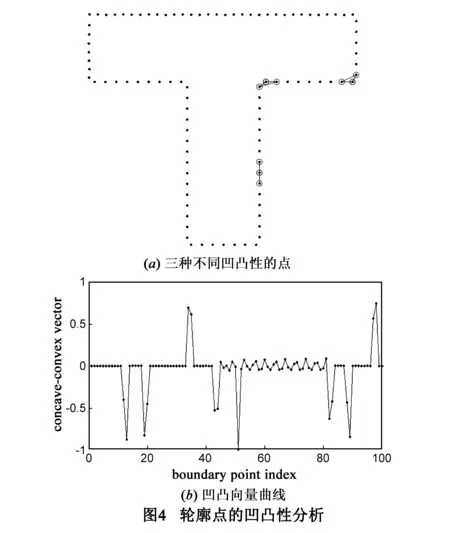
pi点的CBTA描述子Si的第一个元素si,i值的正负表征了该点的凹凸性质.当顺时针采样轮廓点时,该元素为正值表示pi点为凹点,负值表示pi点为凸点,零值表示pi点为直线点.这是因为有向面积si,i是通过计算pi和其相邻两个点pi-1、pi+1坐标的行列式而得,该行列式的正负性能够反映出由这三个点构成的三角形的顺、逆时针方向,而这种顺、逆时针方向恰好对应轮廓的凹凸性.用向量cc=(s1,1,s2,2,…,sn,n)T表示轮廓所有采样点的si,i值集合,由于该向量表征了该点的凹凸性,因此本文称其为凹凸向量(Concave-convex vector).三种不同凹凸性点的标示如图4(a),图4(b)为凹凸向量曲线,该曲线上点的幅值正负对应轮廓采样点的凹凸性,8个尖峰处的点对应字母T中最明显的角点.
综合上述分析表明,CBTA描述子向量不仅包含了轮廓点在形状中的相对位置关系信息,还包含了轮廓的凹凸性信息,这说明该描述子用于轮廓形状特征描述的能力强.另一方面,由于CBTA表示方法描述的是采样点内部之间的相对的几何位置关系,该属性使得其具有平移、旋转不变性.
3 局部平滑抗噪
当轮廓因为变形产生一些变形点时,CBTA描述子会产生一定的偏差,如图5所示,原先D点被变形点D'取代,所构成的同底三角形面积变大.为了提高CBTA描述子的抗噪性,本文采用局部平均的方法来平滑CBTA描述子,使得该描述子对边界变形具有一定的鲁棒性.具体过程如下:

给定一个整数k,将轮廓采样点数n,按[1,k],[k+1,2k],…,[mk-k+1,mk]形式等间隔分成m段,然后计算每一段中k个同底三角形面积的平均值φi,j,即:
(3)
其中j表示分段数的索引,令m=⎣n/k」,则j=1,…,m.用每一段中面积向量的平均值来代替原来k个面积,以平滑变形点带来的偏差.经过上述处理以后,轮廓上第i个采样点的平滑描述子和形状轮廓的平滑描述矩阵分别为:
ψi=(φi,1,φi,2,…,φi,m)T
(4)
Ψ=(ψ1,ψ2,…,ψn)
(5)
局部平滑后的描述子能够使得轮廓点的原始描述子维数由n维降为m维,大大降低了形状匹配代价矩阵的计算复杂度.另外,为了获得CBTA描述子的尺度不变性,本文对描述矩阵的进行局部归一化,即:
(6)
算法复杂度分析:根据式(2),获得每个轮廓点的CBTA描述子要计算n个面积,计算复杂度为O(n),因此获得整个形状的CBTA描述矩阵的时间复杂度为O(n×n)=O(n2).然后根据式(3)对CBTA描述子进行局部平滑,使其从n维降为n/k维,该过程计算复杂度为O(n/k×n)=O(n2)/k.最后利用式(6)对描述矩阵进行局部归一化,该过程算法复杂度仍为O(n2)/k.因此构造一个形状的CBTA描述矩阵的算法复杂度为(1+2/k)O(n2).该算法复杂度要比IDSC(O(n3))低.几种算法对蝴蝶形状-1进行构造描述矩阵花费时间测试结果如表1所示,在该形状上CBTA所用时间较少.

表1 几种算法的描述矩阵构造时间
4 距离计算及形状匹配
利用CBTA矩阵来度量两个形状的距离通常有两个问题要解决:第一,如何计算两个形状轮廓点的描述子之间的距离;第二,如何获得两个形状的轮廓点序列的最优对应关系.对于第一个问题,由于每个轮廓点的CBTA描述子ψ是m维的向量,因此可采用加权L1距离来计算CBTA描述子之间的距离.假设pr,qc分别是两个形状S1,S2的第r个轮廓点和第c个轮廓点,则这两个点的描述子距离或称匹配代价c(pr,qc):
(7)
其中ωt为不同分段的CBTA描述子的权重,考虑到pr,qc附近的点要比距离远的点在目标识别中更重要,应赋给更大的权重,令ωt=1/min{t,m-t}.从而两个形状S1,S2的匹配代价矩阵为:
C(S1,S2)=
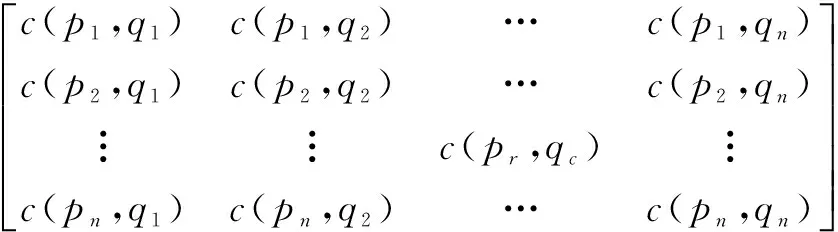
r=1,…,n;c=1,…,n(8)
对于第二个问题,由于轮廓点的顺序信息已知,因此可利用动态规划算法[14](Dynamic Programming,DP)处理匹配代价矩阵.动态规划算法主要目的在于获得形状S1,S2的轮廓点索引的最佳映射π:r→c,该映射应使得式(9)右边最小,最终的形状距离为:
(9)d越小表示两个形状S1,S2越相似.由于两个轮廓序列的最佳映射关系可以通过动态规划算法得到,这使得轮廓序列的起始点位置的不同并不会对最终的匹配结果产生影响,因此在建立CBTA匹配代价矩阵过程中也无需指定起始点.CBTA形状匹配算法的完整流程图如图6所示.

5 混合最小决策检索方法
为了提高形状检索率,本文提出一种形状信息融合的检索方法,该方法将CBTA匹配算法与任意已知的基于轮廓点空间位置关系的形状匹配算法融合,如SC匹配算法.然后利用最小决策公式来更新原始单一的形状距离,即
d(S1,S2)=min(dCBTA(S1,S2),αdSC(S1,S2))
(10)
其中dCBTA为CBTA距离,dSC为SC距离,α为不同的形状匹配距离的惩罚因子.参数α的最终取值应保证混合后检索精度达到最高,该参数的初始值可取两个形状距离矩阵所有元素之和的比值,即
(11)
6 实验与分析
实验参数设置:对轮廓进行等间隔顺时针采样100个点,即n=100;轮廓局部平滑分为20段,即m=20,k=5.实验环境:操作系统Windows7,32位,处理器:Pentium(R)Dual-Core CPU E6700,内存4G,使用软件为Matlab R2011b.6.1MPEG-7形状数据库检索
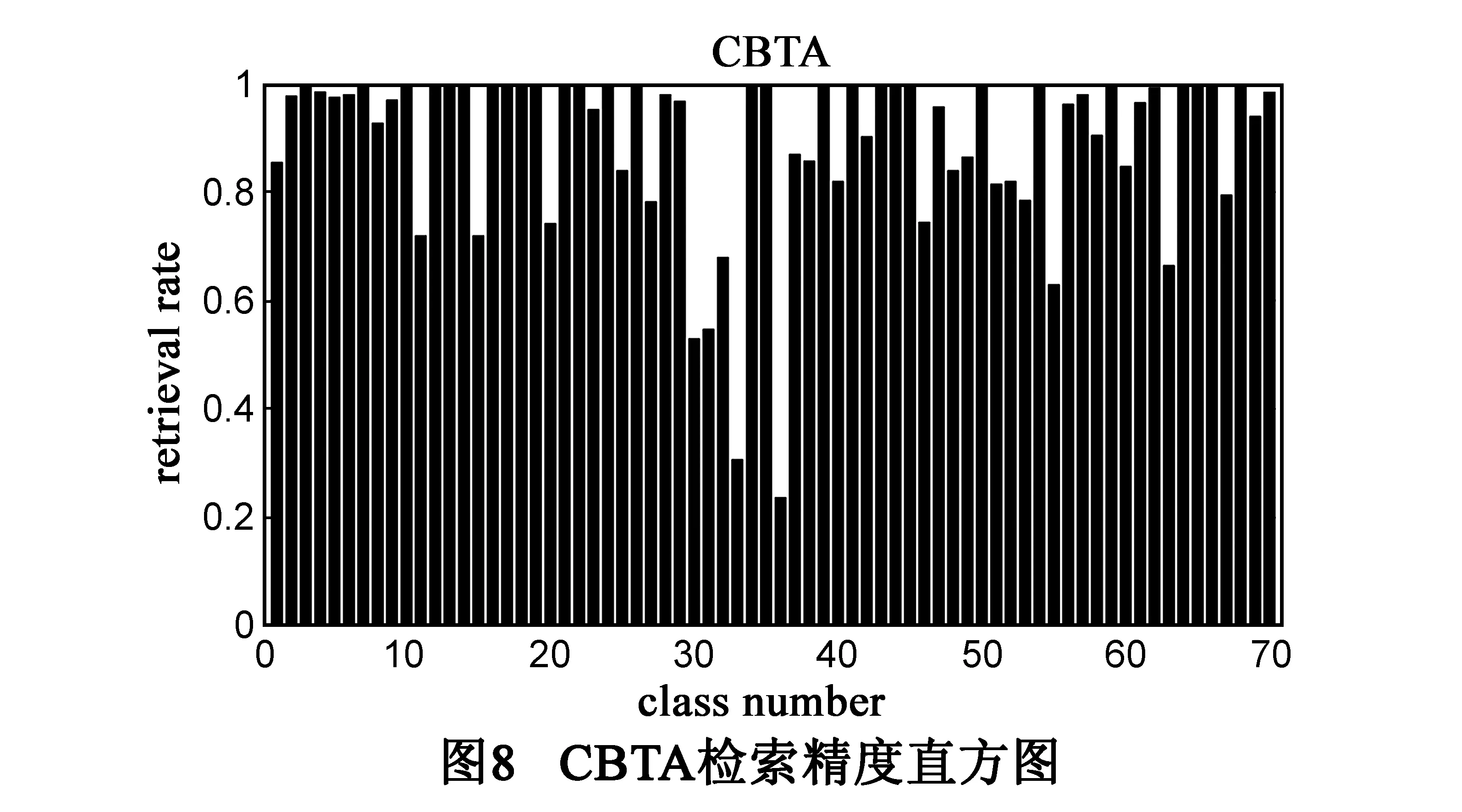
MPEG-7数据库[15]主要用于测试基于相似度的算法的检索精度,是目前衡量形状描述子可靠性的最为重要的基准数据库.该数据库由70类图像组成,每类包含20个形状,共1400个形状.图7是部分MPEG-7形状二值图.通常该数据库采用Bull-eye度量方法获得算法的检索率,即每个形状都作为待匹配形状,然后在剩余形状中找到与待匹配形状最相似的40个形状,若其中包含了与待匹配形状同类的所有20个形状,则该形状的检索率100%,统计每个待匹配形状的40个最相似形状中与该形状是同类的数目,最后再将每个形状的匹配正确数目相加并除以28000(20*1400),即得到形状描述子的检索率.本文提出的CBTA算法检索率为89.45%,高于表2中其他算法.

图8为每一类的检索精度直方图,观察发现,第33类、36类形状的检索率较低,检索率低于40%.这是因为这两类形状中大部分轮廓上都有一道或多道缺口(indentation),包含了复杂的类内信息[17],导致构造的CBTA描述子产生较大偏差,造成了误匹配.

表2 部分重要算法在MPEG-7数据库上的检索率
为了提高MPEG-7数据库的形状检索率,本文将CBTA描述子与SC描述子相混合,并通过最小决策法来获得新的形状距离.首先通过实验获得惩罚因子α的值:根据式(11)得到α的初始值为1.60,由该值向两端计算检索率,表3是α查找结果.由表可知当α=1.56时,混合检索结果最好,为93.65%,比不采用混合检索的CBTA得到的检索率高了4个百分点.此外,利用协同传导度量学习算法,可以将本文的CBTA特征描述子的检索率进一步提高到98.00%.

表3 惩罚因子α查找表
6.2Kimia形状数据库测试
Kimia[18]形状数据库包含Kimia25、Kimia99和Kimia216三个子数据库.本文选取最常用的Kimia99子数据库进行匹配精度测试,如图9所示.Kimia99数据库由9类图像组成,每类有11个形状,共99个形状.在该数据库上,评价算法检索精度的方法为将数据库中所有形状依次作为待匹配形状,计算剩余形状到该形状的相似度,把相似度最大的作为第一相似形状,依次类推,然后统计所有与待匹配形状同类的第一相似到第十相似的形状数量.形状检索结果如表4所示,可以发现本文算法的检索率与其他算法相比均最高.

表4 各种算法在Kimia99数据库上的检索结果
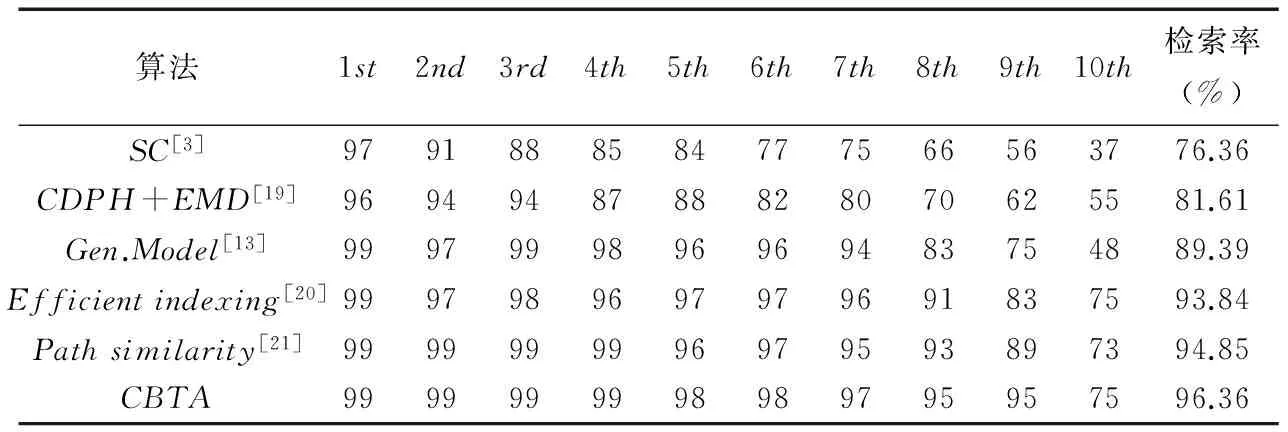
算法1st2nd3rd4th5th6th7th8th9th10th检索率(%)SC[3]9791888584777566563776.36CDPH+EMD[19]9694948788828070625581.61Gen.Model[13]9997999896969483754889.39Efficientindexing[20]9997989697979691837593.84Pathsimilarity[21]9999999996979593897394.85CBTA9999999998989795957596.36
6.3形状铰接变形稳定性测试
铰接形状数据库[4]一般用于测试算法对变形形状识别的稳定性,该数据库一共有40个形状,分为8类,每类包含5个不同角度铰接变形的形状,如图10所示.该数据库上评价算法检索精度的方法与Kimia99类似:将数据库中所有形状依次作为待匹配形状,计算剩余形状到该形状的相似度,把相似度最大的作为第一相似形状,依次类推,然后统计所有与待匹配形状同类的第一相似到第四相似的形状数量.由表5可知,本文提出的CBTA描述子对铰接形状具有较好的表示效果.

6.4抗噪测试

表5 各种算法在铰接形状数据库上的检索结果
为了论证CBTA算法的抗噪性能,本文对Kimia99数据库中所有图形轮廓的x坐标,y坐标加入均值μ=0、标准差由σ=0递增到σ=1.0的高斯噪声,然后在加噪的数据库上进行算法检索对比实验.加噪后的扳手形状如图11所示,检索结果如表6所示.
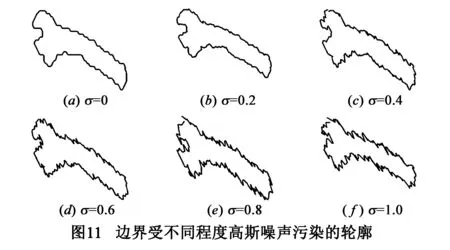
表6 不同噪声水平下的测试结果

σ1st2nd3rd4th5th6th7th8th9th10th检索率(%)09999999998989795957596.360.29999989899989893937996.360.49999999898989994908096.360.69999989899979893877695.350.89999989997979493906694.141.09898989896969395836292.63
由表6可知,在噪声水平0.2到0.6之间算法检索精度几乎不受边界噪声影响,即使在边界变形较大情况下,该算法仍能保持较高的检索精度,这是因为本文对CBTA描述子进行了局部平滑处理,从而提高了CBTA描述子的局部抗噪能力.
7 总结与展望
为了有效解决形状检索中数字图像存在变形的问题,以及提高形状匹配的检索精度和算法运算效率,本文提出了一种基于同底三角形面积的形状描述方法.该方法基于轮廓点的空间位置关系,定义了轮廓点的同底三角形,并以该三角形的面积来描述轮廓点在形状识别中的贡献;然后对同底三角形面积描述子进行局部平滑处理,有效提高了该描述子对噪声的鲁棒性,降低了描述子的维度;采用加权L1距离计算描述子之间的相似度,并利用动态规划算法获得最终的匹配结果.在MPEG-7、Kimia以及铰接形状数据库上的检索测试表明,本文提出的算法能有效匹配出目标,且检索率高于部分重要算法.
本文提出的方法在具有复杂类内信息的形状上的检索率较低,在后续研究中,我们将探索如何有效地提取该类目标的特征信息,增强同底三角形面积描述子对该类形状的区分能力以提高形状检索精度.
[1]吕玉增,彭启民,黎湘.基于极值特征的不变性形状识别[J].电子学报,2008,36(4):679-684.
LuYu-Zeng,PengQi-Min,LiXiang.Shaperecognitionbasedontheinvariantofextremumfeatures[J].ActaElectronicaSinica,2008,36(4):679-684.(inChinese)
[2]周瑜,刘俊涛,白翔.形状匹配方法研究与展望 [J].自动化学报,2012,38(6):889-910.
ZhouYu,LiuJun-tao,BaiXiang.Researchandperspectiveonshapematching[J].ActaAutomaticSinica,2012,38(6):889-910.(inChinese)
[3]BelongieS,MalikJ,PuzichaJ.Shapematchingandobjectrecognitionusingshapecontexts[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2002,24(4):509-522.
[4]LingH,JacobsDW.Shapeclassificationusingtheinner-distance[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2007,29(2):286-299.
[5]郑丹晨,韩敏.基于改进典型形状上下文特征的形状识别方法[J].计算机辅助设计与图形学学报,2013,25(2):215-220.
ZhengDan-chen,HanMin.Improvedshaperecognitionmethodbasedonrepresentativeshapecontext[J].JournalofComputer-AidedDesign&ComputerGraphics,2013,25(2):215-220.(inChinese)
[6]GrigorescuC,PetkovN.Distancesetsforshapefiltersandshaperecognition[J].IEEETransactionsonImageProcessing,2003,12(10):1274-1286.
[7]ElRubeI,AlajlanN,KamelM,etal.Robustmultiscaletriangle-arearepresentationfor2Dshapes[A].IEEEInternationalConferenceonImageProcessing[C].Piscataway,NJ,USA:IEEE,2005.1:I-545-8.
[8]AlajlanN,ElRubeI,KamelMS,etal.Shaperetrievalusingtriangle-arearepresentationanddynamicspacewarping[J].PatternRecognition,2007,40(7):1911-1920.
[9]TemlyakovA,MunsellBC,WaggonerJW,etal.Twoperceptuallymotivatedstrategiesforshapeclassification[A].IEEEConferenceonComputerVisionandPatternRecognition[C].Piscataway,NJ,USA:IEEE,2010.2289-2296.
[10]王斌.一种基于多尺度拱高形状描述的图像检索方法[J].电子学报,2013,41(9):1821-1825.
WangBin,Imageretrievalusingmulti-scalearchheightshapedescription[J].ActaElectronicaSinica,2013,41(9):1821-1825.(inChinese)
[11]BaiX,WangB,YaoC,etal.Co-transductionforshaperetrieval[J].IEEETransactionsonImageProcessing,2012,21(5):2747-2757.
[12]YangX,BaiX,Køknar-TezelS,etal.Densifyingdistancespacesforshapeandimageretrieval[J].JournalofMathematicalImagingandVision,2013,46(1):12-28.
[13]TuZ,YuilleAL.ShapeMatchingandRecognition-usingGenerativeModelsandInformativeFeatures[M].ComputerVision-ECCV2004,SpringerBerlinHeidelberg,2004.195-209.
[14]FelzenszwalbPF,ZabihR.Dynamicprogrammingandgraphalgorithmsincomputervision[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2011,33(4):721-740.
[15]LateckiLJ,LakamperR,EckhardtT.Shapedescriptorsfornon-rigidshapeswithasingleclosedcontour[A].IEEEConferenceonComputerVisionandPatternRecognition[C].LosAlamitos,CA,USA:IEEEComputSoc,2000.424-429.
[16]MokhtarianF,BoberM.CurvatureScaleSpaceRepresentation:Theory,Applications,andMPEG-7Standardization[M].SpringerPublishingCompany,Incorporated,2011.
[17]PremachandranV,KakaralaR.Perceptuallymotivatedshapecontextwhichusesshapeinteriors[J].PatternRecognition,2013,46(8):2092-2102.
[18]SebastianTB,KleinPN,KimiaBB.Recognitionofshapesbyeditingtheirshockgraphs[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2004,26(5):550-571.
[19]ShuX,WuXJ.Anovelcontourdescriptorfor2Dshapematchinganditsapplicationtoimageretrieval[J].ImageandvisionComputing,2011,29(4):286-294.
[20]BiswasS,AggarwalG,ChellappaR.Efficientindexingforarticulationinvariantshapematchingandretrieval[A].IEEEConferenceonComputerVisionandPatternRecognition[C].Piscataway,NJ,USA:IEEE,2007.1-8.
[21]BaiX,LateckiLJ.Pathsimilarityskeletongraphmatching[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2008,30(7):1282-1292.

胡大盟男,1990年生于江苏淮安,硕士研究生,研究方向为计算机视觉.

黄伟国(通信作者)男,1981年生于安徽休宁,副教授,博士,研究方向为数字图像处理.
E-mail:wghuang@suda.edu.cn
Common Base Triangle Area Representation Method for Shape Retrieval
HU Da-meng,HUANG Wei-guo,YANG Jian-yu,ZHU Zhong-kui
(School of Urban Rail Transportation,Soochow University,Suzhou,Jiangsu 215131,China)
Tosolvetheproblemofcontournoiseanddeformationinshapematching,anovelmethodbasedoncommonbasetriangleareaforimprovingretrievalaccuracyandcomputationalefficiencyisproposed.Firstly,acommonbasetriangleareadescriptorofeachsamplepointisdefinedbasedontheareafunctionsofthetrianglesformedbytheothersamplepointsanditstwoneighborpoints.Thenthedescriptorislocalsmoothedtokeepmorecompactandrobust.Secondly,amatchcostmatrixisobtainedbycomputingthecommonbasetriangleareadescriptorsofallthesamplepointsontwoshapes.Finally,thedistancebetweentwoshapesismeasuredbasedonthematchcostmatrixbyDPalgorithm.TheexperimentalresultsofMPEG-7,Kimiaandthearticulationshapedatabaseindicatethatthismethodisrobusttothecontourdeformation,andthecomputationalefficiencyandtheretrievalaccuracyareallessentiallyimproved.
commonbasetriangle;localsmoothing;dynamicprogramming;mixedretrieval;shapematching
2014-10-21;
2015-02-27;责任编辑:蓝红杰
国家自然科学基金(No.51405320,No.61305020);江苏省科研基金(No.BK20130316)
TP391.4
A
0372-2112 (2016)05-1247-07
电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.034
