蜕变关系敏感度及其聚类分析
2016-09-02谢晓东彭声明汪康炜
谢晓东,彭声明,刘 艳,汪康炜,王 田,王 成
(华侨大学计算机科学与技术学院,福建厦门 361021)
蜕变关系敏感度及其聚类分析
谢晓东,彭声明,刘艳,汪康炜,王田,王成
(华侨大学计算机科学与技术学院,福建厦门 361021)
为缓解软件测试的Oracle问题,蜕变测试通过验证多个测试用例及其输出之间是否满足蜕变关系来验证测试结果.可见蜕变关系是蜕变测试的核心,而现有的蜕变关系检错能力的衡量标准,即错误检出率(Failure Detecting Rate,FDR)是蜕变关系对不同变体的错误检出概率的平均值,这掩盖了蜕变关系的一些重要特征.因而本文提出蜕变关系敏感度的概念,即用蜕变关系对不同变体的错误检出率所构成的多维信息向量,来全面地反映蜕变关系特征,从而为蜕变测试研究提供更多的可能性.蜕变关系敏感度的一个典型应用是对蜕变关系集合进行聚类分析,并挖掘出构建蜕变关系的需求特征与错误发现能力之间的关联.论文使用经典聚类算法k-means进行了实验.实验结果表明,蜕变关系敏感度能很好地支持聚类分析计算,并能挖掘出有用的知识.蜕变关系敏感度为蜕变测试的进一步研究提供了新的方法和依据.
蜕变测试;蜕变关系;蜕变关系敏感度;聚类算法
1 引言
为缓解软件测试中的Oracle问题[1],Chen[2~4]提出了蜕变测试方法.蜕变测试通过验证待测试程序的多个测试用例及它们的输出结果之间是否满足特定的关系(称之为蜕变关系)来确认待测程序是否存在错误.蜕变测试无需构造预期输出即可验证执行结果的正确性,从而缓解了Oracle问题.蜕变关系是蜕变测试的核心,是根据被测程序的需求特征或约束关系等构造而成的.根据待测程序的需求可以构造出大量的蜕变关系[5].这些蜕变关系从不同侧面表达了待测程序部分需求信息和隐式约束.
对蜕变关系进行研究的一个重要内容是对其检错能力进行分析.目前通常采用错误发现率FDR(failure detecting ration)来刻画蜕变关系的检错效率[6].Cao[7]等研究了BCMD等6种不同的先验衡量方法,通过分析源用例和衍生用例之间执行路径的差别来预测蜕变关系的检错能力,该研究以FDR为基准.而Dong等在研究复合蜕变关系中也使用了FDR[8,9].然而,FDR从统计上掩盖了蜕变关系检错能力的一个重要特征:多维特性,即蜕变关系对不同类型的错误的检错能力是不同的.这使得在研究中可能因缺乏必要的信息难以进行更进一步的分析.例如,对蜕变关系进行基于检错能力的分类,仅依靠FDR将无能为力.
针对蜕变关系检错能力的多维特性,本文提出了蜕变关系敏感度的概念,即用多维信息向量来表示蜕变关系对不同变体的错误发现率.敏感度的每一维都代表蜕变关系对某个变体或变体子集的检错效率.敏感度从整体上刻画了蜕变关系的检错能力的特征,更大程度地保留相关信息,从而为蜕变测试的研究提供了更好的检错能力分析依据和可能性.
例如,聚类分析是一种常用的数据挖掘方法,主要用于将对象分类并分析其相似性[10,11].蜕变测试中可以产生大量的蜕变关系,这些蜕变关系所表达的需求信息和约束对程序正确性的影响是非常重要的研究内容.基于蜕变关系敏感度,可以使用聚类算法,如k-means进行分类并分析它们之间的关联,而FDR对此无能为力.
2 相关背景
蜕变测试是一种黑盒测试技术,它是通过验证蜕变关系来确认待测程序是否存在错误.例如,当测试sin(x)的程序时,很难直接得到测试用例x=29的预期输出.但可以利用sin函数的特性:当90>x1>x2>0时,有sin(x1)>sin(x2),从而通过验证sin(30)>sin(29)是否成立来判断待测程序是否存在错误.
通常执行一次蜕变测试需要进行以下4个步骤:(1)选择一个源用例,如上述例子中的x1=29;(2)根据蜕变关系和源用例,给出相应的衍生用例,如上例中的x2=30;(3)分别执行源用例和衍生用例,得到它们的执行结果;(4)检查源用例、衍生用例及它们的执行结果是否满足蜕变关系,如果满足则该次测试通过,否则就发现一个错误.
从一个待测程序的需求可以产生很多蜕变关系.例如,根据sin函数的特征,可以给出诸如sin(x)=sin(180-x),sin(x)=sin(360+x),sin(x)=sin(720+x),…,等多个蜕变关系.理论上,任一待测程序的蜕变关系是无穷多的.因此如何衡量和选择检错能力高的蜕变关系用于蜕变测试是一个重要的研究课题.
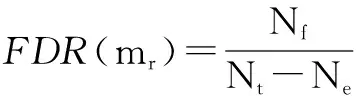
3 蜕变关系敏感度模型
3.1蜕变关系敏感度定义
FDR的定义隐含着一个假设:蜕变关系对不同错误的揭示能力是相同的.然而这不正确.例如,令程序P实现了函数f(a,b)=a*b,根据乘法满足交换律的特征,可以构造蜕变关系MR:f(a,b)=f(b,a).对该程序的两个变体,m1(a,b)=a+b,m2(a,b)=a-b,MR很难发现变体m1的错误,却能轻易发现m2的错误.因为m1的错误之处是乘法变成加法,而加法也满足交换律,MR无法区分变体和正确程序.因此,蜕变关系对不同的错误有不同的揭示能力.而FDR用平均值来衡量蜕变关系的检错能力,掩盖了蜕变关系的这一特性.

蜕变关系敏感度是一个多维信息向量,当需要对多个蜕变关系进行排序时,可以通过简单的统计函数转化为某种形式的标量,例如将各维分量进行简单的求和或取平均值.使用退化后的度量值对蜕变关系进行排序的结果和使用FDR近似.
显然,蜕变关系敏感度是将FDR细化到了每一变体上,从而避免由于平均化而从统计上掩盖各蜕变关系在错误检出能力上的差异.
3.2基于变体子集的蜕变关系敏感度
在3.1节的讨论中所给出的蜕变关系敏感度的维度等于变体个数,这使得敏感度的维度过高不利于后续的比较.因此,可以采用某些简化的方法得到维度较低的蜕变关系敏感度.

显然,基于变体子集的蜕变关系敏感度大大降低了维度,从而降低比较蜕变关系检错能力的难度.如何划分变体集合,对敏感度的计算结果有很大的影响.特别的,当将变体集合仅划分成一个子集,那么蜕变关系敏感度将退化成为FDR.在本文的研究中,把通过同一变异算子所产生的变体划分为一个子集.由于变异算子的典型性,这种划分方式使得同一子集中的变体具有一定程度上的相似性,所得到的敏感度与蜕变关系检错能力更具有相关性.
4 基于蜕变关系敏感度的聚类分析算法
蜕变关系敏感度是蜕变关系研究的一种基础度量,可以运用于各种场合.对蜕变关系集合进行聚类分析是一种典型的应用.
在蜕变测试研究和应用中,常常会产生大量的蜕变关系.这些蜕变关系之间存在着一定的关联,如有些蜕变关系由相同或相似的需求衍生而来,或有部分蜕变关系是由其他蜕变关系复合而成的.因此,如果能将这些蜕变关系分类,对研究和应用蜕变关系有重要的意义.
对大量蜕变关系进行敏感度分析,可得到一个敏感度矩阵.得到敏感度矩阵后,即可使用经典的聚类算法K-means对蜕变关系进行聚类分析,如算法1所示.算法中的另一输入参数,蜕变关系类型数量k,可根据蜕变关系的相关特征事先指定,也可通过其他算法如层次聚类算法进行初步分析得到.

5 实验
为验证蜕变关系敏感度对蜕变关系检错能力的评价及使用算法1进行聚类分析的可行性,进行了一系列相关实验.
5.1实验程序及变体
实验选取了一个图论的程序代码以及一个日期计算程序作为被测程序.第一个程序实现了迪杰斯特拉最短路径算法(Dijkstra's Shortest Path Algorithm,DSPA).该算法是在一个无向图G中,寻找节点a到节点b的最短路径.第二个程序(Days)的输入为两个日期的年月日,输出为这两个日期相差的天数.
实验程序的变异是通过工具MuJava实现的,各实验程序使用变异算子得到的变体的数目如表1所示.在后续研究中,变体集合根据变异算子进行划分.对DSPA程序,共构造了9个蜕变关系(MR1~MR9),基本情况如表2所示.对Days程序,共构造了10个蜕变关系(MR-1~MR-10),基本情况如表3所示.

表1 实验程序的变体情况
5.2实验步骤和实验结果
在实验过程中,首先生成实验程序的变体.然后为每一实验程序生成一个包含1000个用例的测试用例集合,该集合的测试用例将作为蜕变测试中的源用例.对DSPA程序所需要的无向图,每一无向图中至少包含10个顶点,无向图中顶点的个数、顶点之间是否存在边、边的权重等内容均随机生成.而作为DSPA输入参数的起点和终点也从无向图中随机选择.衍生用例根据蜕变关系和源用例产生.而对Days程序,所输入的年月日数据都是简单的整数,因此测试用例的数据是在取值范围内随机进行选择.
使用源用例和衍生用例对变体进行测试,并统计变体被杀死的情况,可得到相应蜕变关系集合的敏感度矩阵,表4为DSPA的敏感度矩阵,表5为Days的敏感度矩阵.
为使用蜕变关系敏感度对蜕变关系检错能力进行评价,表6给出了各蜕变关系的FDR值及平均敏感度.根据算法1,对MR1~MR9以及MR-1~MR-10分别进行了聚类分析,分析中类别数目设定为2,分析结果如表7所示.

表2 DSPA的蜕变关系

表3 Days的蜕变关系
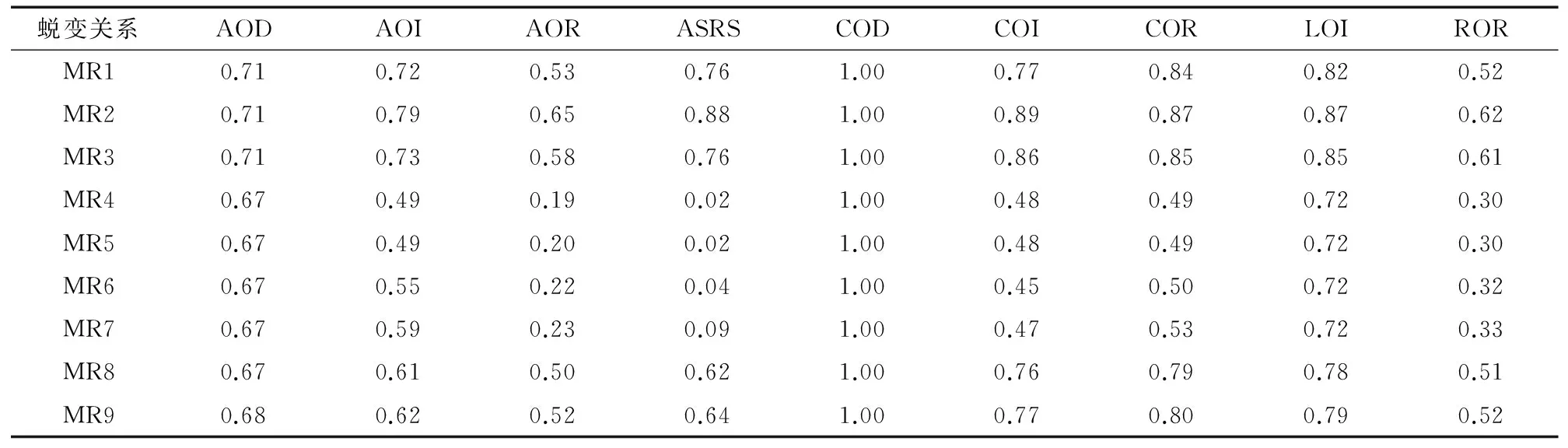
表4 DSPA蜕变关系的敏感度矩阵
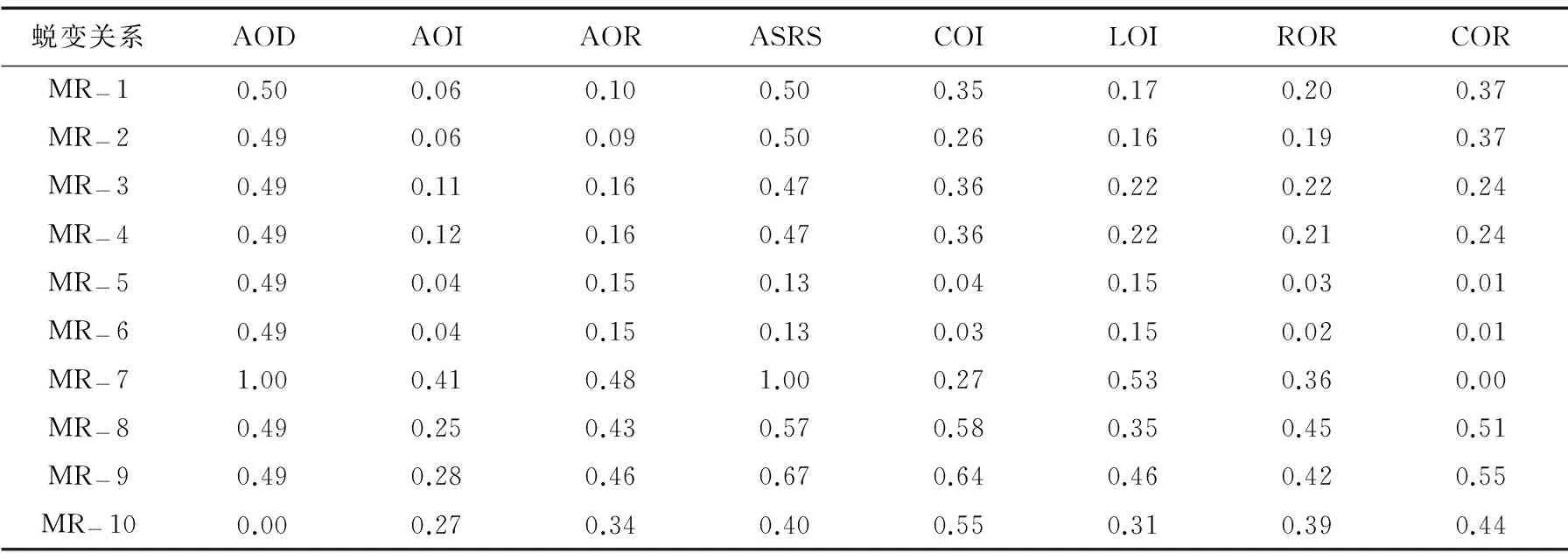
表5 Days蜕变关系的敏感度矩阵
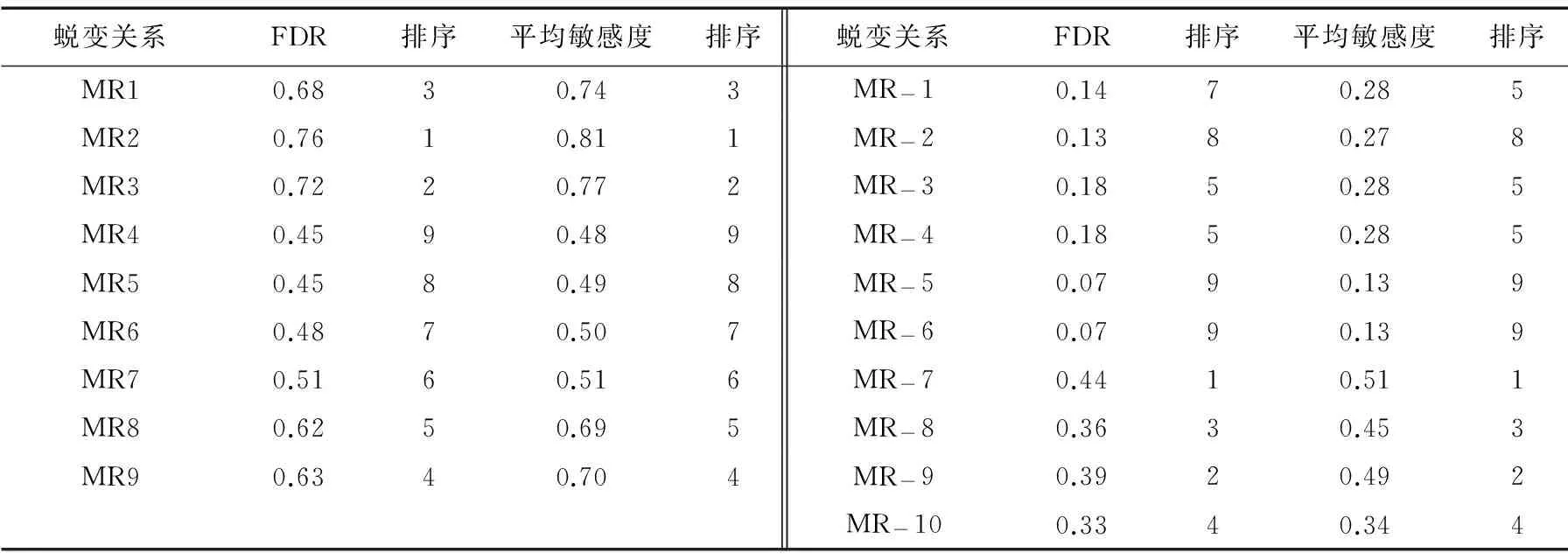
表6 FDR与平均敏感度

表7 基于敏感度的聚类
5.3实验结果分析
从表6可以看出,根据FDR和平均敏感度对DSPA蜕变关系的进行检错能力的排序结果相同.Days蜕变关系的排序结果中,原来MR-5=MR-6>MR-2变成了MR-5=MR-6=MR-2.其原因在于,实验中使用了子集划分法简化敏感度,当对简化敏感度求平均值时,实际上是对原始的敏感度进行了加权平均.而FDR是原始敏感度的简单平均值.因此在子集划分中,如果某个子集的变体数目偏少,那么该子集的变体的权重较大.实验中,COR和AOD的变体数较少,因而蜕变关系对相应子集变体的检错能力对敏感度平均值有较大的影响.
从表7可以看出,通过基于敏感度的蜕变关系聚类分析算法,将DSPA的蜕变关系划分为{MR4,MR5,MR6,MR7}和{MR1,MR2,MR3,MR8,MR9};而Days的蜕变关系被划分为{MR-1,MR-2,MR-3,MR-4,MR-5,MR-6}和{MR-7,MR-8,MR-9,MR-10}.结合各蜕变关系本身的特征,可以归纳出一些知识:(1)起点终点参数对DSPS实验程序有较为重要的影响;(2)在Days实验程序中,对年月日进行增减这一类的蜕变关系,其错误检出能力较小.
6 结束语
蜕变测试能有效地缓解传统软件测试中的Oracle问题.蜕变关系对蜕变测试至关重要,也是蜕变测试的研究重点.现有文献中使用FDR作为蜕变关系检错能力的衡量准则,使得蜕变关系检错能力的多维特性被掩盖了.蜕变关系敏感度是由蜕变关系对不同变体的检错效率构成的多维信息向量,能更加全面地反映蜕变关系的多维特性,从而更有力地支持蜕变测试的研究.
本文给出了蜕变关系敏感度及简化的基于变体子集划分的蜕变关系敏感度的定义和计算方法.在此基础上使用k-means聚类算法对蜕变关系集合进行分类.实验表明蜕变关系敏感度能很好地支持聚类分析,并能得到蜕变关系的有意义的知识.
蜕变测试研究中的一个难点是:每一蜕变关系都是从软件需求中抽取的,蜕变关系之间的联系很难定义,进而难以得到蜕变关系之间的共性.蜕变关系敏感度的引入,从检测能力的角度揭示了蜕变关系之间的联系,为蜕变关系的错误检测能力研究提供了一个新的视角和工具.因此蜕变关系敏感度将有力地推动蜕变测试的研究.
在本文后续研究中,将对变体子集划分策略做进一步的研究.此外,采用更加有效的聚类算法,如层次法,用于蜕变关系的聚类分析研究也是将来的研究内容之一.
[1]EJ Weyuker.On testing non-testable programs[J].The Computer Journal,1982,25(4):465-470.
[2]F Chan,TY Chen,SC Cheung,M Lau,S Yiu.Application of metamorphic testing in numerical analysis[A].In Proceedings of the Lasted International Conference on Software Engineering[C].New York:ACM Press,1998.191-197.
[3]TY Chen,SC Cheung,SM Yiu.Metamorphic testing:A new approach for generating next test cases[R].Technical Report HKUST-CS98-01,Department of Computer Science,Hong Kong University of Science and Technology,1998.1-11.
[4]TY Chen,TH Tse,ZQ Zhou.Fault based testing in the absence of an oracle[A].In Proceedings of the 25th IEEE Annual International Computer Software and Applications Conference[C].New York:IEEE Computer Society,2001.172-178.
[5]Mayer,Johannes,Ralph Guderlei.An empirical study on the selection of good metamorphic relations[A].In Proceeding of 30th Annual International Computer Software and Applications Conference[C].New York:IEEE Computer Society,2006.475-484.
[6]TY Chen,DH Huang,TH Tse,ZQ Zhou.Case studies on the selection of useful relations in metamorphic testing[A].In Proceedings of the 4th Ibero-American Symposium on Software Engineering and Knowledge Engineering[C].New York:IEEE Computer Society,2004.569-583.
[7]Y Cao,ZQ Zhou,TY Chen.On the correlation between the effectiveness of metamorphic relations and dissimilarities of test case executions[A].In Proceedings of 13th International Conference on Quality Software[C].New York:IEEE Computer Society,2013.153-162.
[8]Dong GW,Xu BW,Chen L,Nie CH,Wang LL.Case studies on testing with compositional metamorphic relations[J].Journal of Southeast University (English Edition),2008,24(4).437-443.
[9]Asrafi M,Liu H,Kuo FC.On testing effectiveness of metamorphic relations:A case study[A].In Proceedings of Fifth International Conference on Secure Software Integration and Reliability Improvement[C].New York:IEEE Computer Society,2011.147-156.
[10]J MacQueen.Some methods for classification and analysis of multivariate observations[A].In Proceedings of Fifth Berkeley Symposium on Mathematical Statistics and Probability[C].University of California,1967.281-297.
[11]PS Bradley,Usama M Fayyad.Refining Initial Points for K-Means Clustering[M].New York:John Wiley and Sons,1998.56-67.

谢晓东(通信作者)男,1976年10月出生,江西赣州人,讲师、博士.分别在1997年、2000年和2007年于华中科技大学获得工学学士、工学硕士和工学博士学位.1997年留校任教,2011年至今在华侨大学计算机科学与技术学院任教.
E-mail:xiaodongxie@hqu.edu.cn

彭声明男,1990年4月出生,安徽安庆人,硕士研究生.2013年于安庆师范学院获得工学学士学位.2013年至今在华侨大学计算机科学与技术学院攻读硕士学位.
E-mail:pengshen0404@qq.com
Sensitivity of Metamorphic Relationships and Its Cluster Analysis
XIE Xiao-dong,PENG Sheng-ming,LIU Yan,WANG Kang-wei,WANG Tian,WANG Cheng
(CollegeofComputerScienceandTechnology,HuaqiaoUniversity,Xiamen,Fujian361021,China)
Metamorphic testing (MT) is proposed to alleviate oracle problem in software testing,which verifies software under testing (SUT) by checking whether inputs and outputs satisfy metamorphic relation (MR).MR,the constraint constructed from the propriety of SUT,plays a key role in MT and becomes focus in MT researching.Failure detecting ratio (FDR) is a popular measure for failure detecting ability of MR.However,FDR is the mean of failure detecting ratios of a MR applied on different mutants.This averaging covers some important properties of MR.In this paper,sensitivity of MR is defined,which is a multi-dimension information vector consisted of failure detecting ratios on all mutants.Sensitivity of MR reflects more fully characteristics of MR than FDR and allows more possibility in MT researching.One typical application of sensitivity of MR is the cluster analysis on MR set,in order to find some clues of the underlying relevant between the requirement of MR and its failure detecting ability.K-means algorithm,a classical cluster analysis algorithm,based on MR sensitivity is applied in the experiment.The experiment results show that the sensitivity of MR supports cluster analysis strongly and the analysis offers some useful knowledge.Sensitivity of MR will be a good method and essential rationale for MT researching.
metamorphic testing;metamorphic relation;metamorphic relation sensitivity;cluster analysis algorithm
2015-08-19;
2016-02-01;责任编辑:马兰英
国家自然科学青年基金(No.61103053,No.61202106,No.61572206);福建省自然科学基金(No.2013J01238);厦门市科技计划项目(No.3502Z20143041)
TP311.1
A
0372-2112 (2016)05-1196-06
电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.026
