考虑延误时间成本的最优路边停车策略研究
2016-09-02田琼,罗婷,杨丽
田 琼, 罗 婷, 杨 丽
(北京航空航天大学经济管理学院, 北京 100191)
考虑延误时间成本的最优路边停车策略研究
田琼, 罗婷, 杨丽
(北京航空航天大学经济管理学院, 北京 100191)
本文研究了延误时间成本作用下,出行者面对路边停车空位随机分布的寻位策略选择.出行者将做出提前多久出发和提前多远寻位的组合决策,其成本不但包括确定的路上行驶成本,还包括依赖于实时变化路边停车空位分布的延误时间成本和期望寻车成本.依据出行者到达目的地可能的延误状态,区分了三种不同的寻位策略,其中“不早到”策略被证明不可能成为最优选择,而“早停早到”策略和“早停迟到”策略则在不同条件下可能成为最优选择,尤其是单位迟到时间成本小于单位早到时间成本时,“早停迟到”策略是最优停车策略.算例结果支持了模型分析的结论.
路边停车; 延误时间成本; 停车策略; 寻位成本
0 引 言
截至2013年底,北京机动车保有量已超540万辆,而政府公布的正规停车位仅有276万个,实际非正规停车比例超过80%,其中大量是路边停车[1].IBM公司2011年在全球20个城市展开调查[2],发现在这些城市平均超过30%的交通是由于司机寻找路边停车位引发的,部分城市中心区高峰期70%以上的交通量是寻位车流.
在路边停车理论研究方面,国内外管理学家和经济学者们在20世纪90年代主要关注于路边停车对动态交通的干扰、路边停车市场均衡、路边停车过程中的关键影响因素以及停车政策分析.Glazer等[3],Armonk[4]以及Verhoef等[5]建立了规范的经济学模型研究路边停车市场的均衡以及停车政策的影响.近年来的相关理论研究越来越多地关注停车寻位会造成过度的车辆出行、拥挤以及温室气体的排放等外部性.Button等学者就认为车辆巡游找位与道路瓶颈排队一样,属于资源错配[6,7],Calthrop等认为对系统最优的控制应该利用经济手段尽量消除[8, 9].
在实证方面,van Ommeren等做了两篇关于找停车位的相关实证研究[10,11],Kobus等也对路边停车收费对司机对路边停车和路外停车进行选择的影响进行了实证[12].这一系列的实证研究表明,由于路边停车市场供给与需求的随机性,使得不可能完全消除寻位行为.这就引发了如何对路边停车寻位合理控制的思考,比如Shoup依据他在美国旧金山和洛杉矶的研究,建议路边停车的收费水平应该设定在使得平均泊位占有率维持在85%的水平而不是把完全消除寻位现象作为目标[13].
已有的研究大多关注于路边停车寻位的总体数据,比如平均寻位距离、平均泊位占有率和平均停车时长等,对驾驶者的具体出行选择行为研究较少.其实从行为建模的角度研究交通问题,国内外学者都做了很多的尝试,比如基于展望理论对出行风险的认知和评价[14],考虑出行者出行时间选择的影响[15],应用Logit模型考虑出行者在出行模式上的随机选择[16]等.
本文将交通瓶颈模型[17]中的延误时间成本考虑进来,出行者有理想的到达目的地的时间,早到或晚到都会产生相应的成本.为了规避风险,降低期望成本,出行者将在出行前决定提前多久出发和提前多远开始寻位,最优的路边停车策略将最小化其期望总成本.本研究有助于加深对城市出行者停车寻位行为的认识,为路边停车位的合理规划和科学管理提供决策依据和理论支持,以期减少停车寻位车流,缓解城市中心城区交通高峰拥堵.
1 模型的建立
本文基本模型参照1999年Arnott教授提出的环形城市模型[18,19],该模型因其形式简洁,易于扩展,而被广泛应用.如图1所示的环形城市,城市中每个点的空间结构和出行者的出行需求都是同质的,出行者从O出发,沿着环形道路单向顺时针到距离为d的地方D办事.路边均匀分布的停车位部分被其他车辆随机占用.出行者不知道空闲车位的实时分布,但依据经验,知道寻位距离的概率密度函数f(y)(即寻位y距离停下车的概率).设出行者办事有理想的到达时间,比这个时间早到或者迟到都会造成额外的成本.由于寻位过程的随机性,出行者的理性选择将是提前出发并在到达目的地前提前寻位,其出行过程具体如下:先正常行驶至Q;从Q开始寻找路边停车位,直到在S处成功停车为止;随后步行至目的地,在目的地办事;步行回到停车位准备下一个出行.

图1 路边停车过程示意图
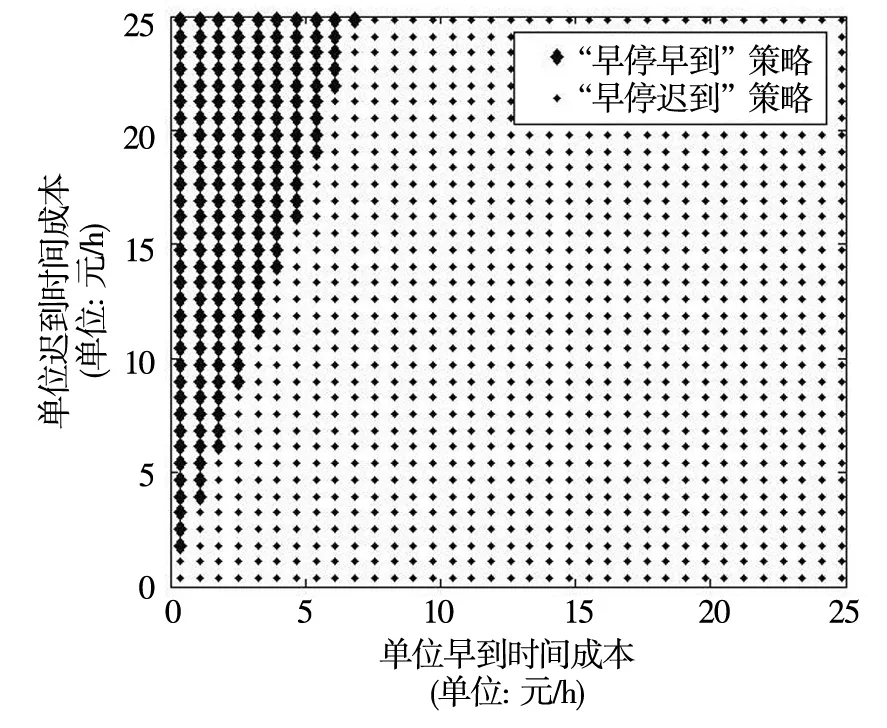
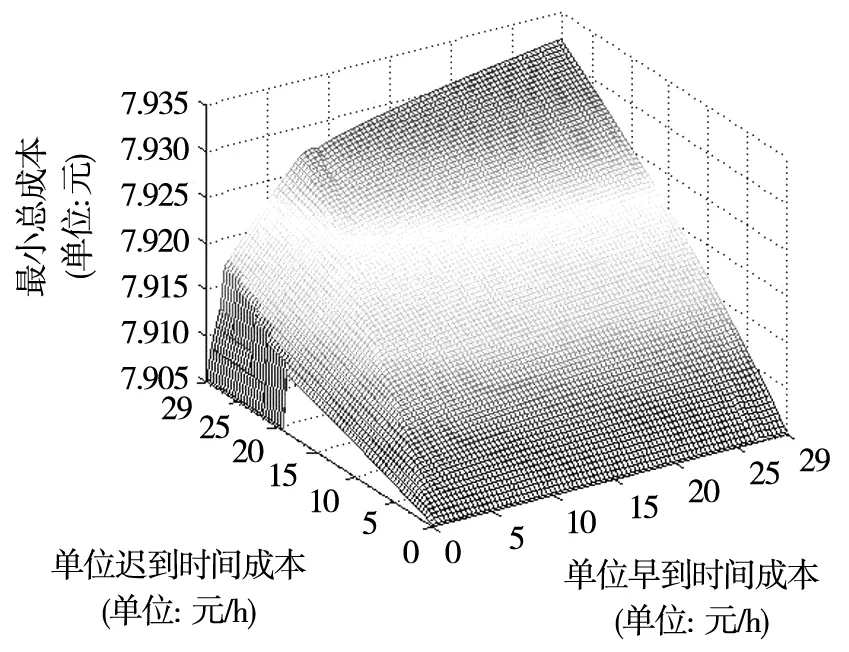
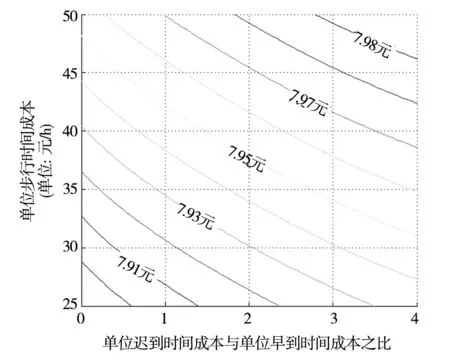
符号和参数:vf—普通驾驶速度,vc—寻位过程中速度,vw—出行者的步行速度,假设三个速度满足关系vw 出行者的出行成本由五部分组成,分别是普通驾驶时间成本、找停车位的寻位时间成本、步行时间成本三项行程时间成本、停车收费以及早到或迟到目的地的延误时间成本.为了便于分析和比较,行程时间成本、延误时间成本均换算成货币成本,具体形式如下. 出行者的普通驾驶时间成本 cf(x)=α1(d-x)/vf (1) 出行者的寻位时间成本 cc(y)=α2y/vc (2) 出行者的步行时间成本 (3) 出行者的停车收费 (4) 出行者的延误时间成本 (5) 其中实际寻位距离y是一个随机变量,出行者的实际途中时间T(x,y)为 (6) 因此,出行总成本可用下式表达 (7) 出行者可以决定的只有提前出发时间tad和提前寻位距离x两个变量,因此出行者面临的优化问题为选择提前出发时间和提前寻位距离使自身期望成本最小化 (8) E[cf(x)]=α1(d-x)/vf (9) E[cc(y)]=α2E(y)/vc=α2G(+∞)/vc (10) (11) (12) 而延误时间成本的期望表达式与出行者停车寻位的策略有关,需要进一步讨论. 由于寻位的距离y是随机变量,出行者最终到达目的地后是早到、迟到还是准时,将存在变数.本节将依据出行者可能面对的延误情况,将其寻位策略分为三种考虑.在这之前,分析影响其延误的两个重要指标. 当出行者刚开始寻位时就立刻找到路边停车位时,其实际途中时间为T(x,0)=(d-x)/vf+x/vw,即y=0时的实际途中时间.而出行者直到达到目的地时才正好找到路边停车位的实际途中时间为,T(x,x)=(d-x)/vf+x/vc,即y=x时的实际途中时间. 当实际寻位距离y小于提前寻位距离x时,由于驾车寻位速度要大于步行速度,实际途中时间T(x,y)会随实际寻位距离的增大而减小,特别的,有T(x,x) 依据T(x,x),T(x,0)和提前出发时间tad的关系,将出行者的寻位策略分为三种,即“早停早到”、“早停迟到”和“不早到”策略. 定义1当T(x,0) 这时出行者在刚开始寻位的位置Q点找到停车位时到达目的地会早到. 定义2当T(x,0)>tad,而T(x,x) 这时出行者在刚开始寻位的位置Q点找到停车位时到达目的地会迟到,而在目的地D点处找到停车位到达目的地会早到. 定义3当T(x,x)>tad时,称之为“不早到”策略. 此时最短途中时间都大于提前出发时间,那么无论出行者在何处找到停车位,到达目的地时都不会早到.下面将具体分析这三种策略的延误成本. 2.1“早停早到”策略 在这种策略下,T(x,x) x<(tad-d/vf)/(1/vw-1/vf) (13) 显然有T(x,x) ydown=[tad-d/vf+(1/vf+1/vw)x]/ (1/vc+1/vw). 在“早停早到”策略下,可能发生图2所示的三种延误情况:1)停车地点还没到目的地,最后到达目的地早到了;2)停车地点已经过了目的地,最后到达目的地早到了;3)停车地点已经过了目的地,最后到达目的地迟到了. 图2 “早停早到”策略下的延误情况分布 “早停早到”策略下的延误时间成本的分段函数为 (14) (15) 2.2“早停迟到”策略 这时有T(x,0)>tad和T(x,x) (tad-d/vf)/(1/vw-1/vf) (tad-d/vf)/(1/vc-1/vf) (16) 在这种情况下,出行者在Q点和D点之间的某一点找到车位时会准时到达目的地.随着寻位的地点越过了D,实际途中时间逐渐增大,又会开始出现迟到现象.此时寻位距离y存在两个准时到达分界点yup=[tad-d/vf+(1/vf-1/vw)x]/(1/vc-1/vw),ydown=[tad-d/vf+(1/vf+1/vw)x]/(1/vc+1/vw). 在“早停迟到”策略下,可能会发生图3所示的四种延误情况:1)停车地点还没到目的地,最后到达目的地迟到了;2)停车地点还没到目的地,最后到达目的地早到了;3)停车地点已经过了目的地,最后到达目的地早到了;4)停车地点已经过了目的地,最后到达目的地迟到了. 图3 “早停迟到”策略下的延误情况分布 “早停迟到”策略下的延误时间成本的分段函数为 (17) (18) 2.3“不早到”策略 该策略下,T(x,x)>tad,等价于 x>(tad-d/vf)/(1/vc-1/vf) (19)这时不存在准时到达分界点.在“不早到”策略下,可能会发生图4所示的两种延误情况:1)停车地点没到目的地,最后到达目的地迟到了;2)停车地点过了目的地,最后到达目的地迟到了. 图4 “不早到”策略下的延误情况分布 “不早到”策略下的延误时间成本的分段函数为 (20) (21) 出行者将选择(tad,x)变量组合来决定提前多久出发和提前多远寻位来最小化期望出行总成本,这最小化的决策组合所对应的寻车策略,就是最优寻车策略.该最小化问题的一阶条件为 ∂E[c(tad,x,y)]/∂tad=0 (22) ∂E[c(tad,x,y)]/∂x=0 (23) 可以注意到,在“不早到”策略下,期望总成本对提前出发时间的一阶导数始终为-γ,即出行者总是可以通过提前出发降低期望总成本,说明“不早到”策略不可能称为最优选择,最优停车策略只能在“早停早到”策略和“早停迟到”策略中产生. 在“早停早到”策略下,一阶条件等价于 F(ydown)=γ/(β+γ) (24) F(x)=[2α3+2τ+(vw/vf)α1]/ (4α3+4τ-2β)>1/2 (25) 由式(25)得到性质1. 性质1在早停早到是最优的前提下,则出行者将有50%以上概率在到达目的地前找到车位. 在性质1里面“找到车位的概率大于50%”其实是“早停早到”策略最优下的必要条件,而不是其充要条件.这里之所以强调这个必要条件,是为了说明,当停车司机选择了“早停早到”这一寻位策略时,在开始寻位地点的选择上一定会找一个在到达目的地前比超过目的地后有更大可能性找到空位的点. 由于ydown>x,有F(ydown)>F(x),再结合式(24)和式(25),由此得到“早停早到”策略下有局部最优解需要满足 (26) 式(26)说明,“早停早到”策略成为最优的条件不仅要求单位迟到时间成本大于单位早到时间成本,而且要大到一定程度否则“早停迟到”策略是最优停车策略.由此得到性质2 性质2如果单位迟到时间成本小于单位早到时间成本,“早停迟到”策略是最优停车策略. 在“早停迟到”策略下,即当 (tad-d/vf)/(1/vw-1/vf) F(ydown)-F(yup)=γ/(β+γ) (27) (28) 这时yup、x、ydown三者存在关系式x=[(1-vw/vc)/2]yup+[(1+vw/vc)/2]ydown. 依据实证[11],假设寻位成功概率随距离增加而减少,即f′(y)<0,F(y)的二阶导数小于0,则有 F(x)>[(1-vw/vc)/2]F(yup)+ [(1+vw/vc)/2]F(ydown) 结合式(27)和式(28),得到“早停迟到”策略下有局部最优解需要满足的必要条件有 (29) 式(29)说明“早停迟到”若要成为最优策略,β不能过小,即 性质3在单位迟到时间成本给定时,如果单位早到时间成本不高,“早停迟到”策略不是最优停车策略,此时“早停早到”策略是最优停车策略. 又由于ydown>x>yup,有 F(ydown)>F(x)>F(yup),可以得到 F(x)>[(2α3+2τ)/vw+α1/vf]/ [(4α3+4τ+2γ)/vw] (30) F(x)<[(2α3+2τ+2γ)/vw+α1/vf]/ [(4α3+4τ+2γ)/vw] (31) 式(30)中可以看出如果α1/vf<γ/vw,即同等距离下,自由流开车成本大于步行迟到成本,则F(x)>1/2,得到性质4. 性质4如果单位距离的自由流开车成本大于步行迟到成本,“早停迟到”策略下最优提前寻位距离x将保证50%以上概率在到达目的地前找到车位. 结合式(24)、式(25)、式(27)以及式(28),“早停早到”策略和“早停迟到”策略的最优一阶条件中都没有单位寻位时间成本α2这个变量,得到性质5. 性质5单位寻位时间成本不影响出行者的最优出行策略选择. 本节用算例验证前面模型的分析.算例取值参照北京收费数据和一般车辆参数.算例基本输入参数:(α1,α2,α3,τ)=(20,25,30,20)(元/h),(vf,vc,vw)=(20,5,5/3)(m/s),寻位距离y的概率密度函数f(x)=ae-ax,其中a=0.01,经济含义是寻位距离的期望为10m. 图5给出了不同的单位早到时间成本和单位迟到时间成本取值下的最优停车策略选择的变化情况.单位迟到时间成本增加,出行者会偏向于选择“早停早到”策略,验证了前文最优成本性质分析中的性质2和性质3. 图5 早到-迟到成本下最优策略选择图 图6给出了不同的单位早到时间成本和单位迟到时间成本取值下的最小总成本的变化情况,可以看到随着单位早到时间成本和单位迟到时间成本增大,最小总成本变大. 图6 延误时间成本-最小总成本图 图7给出了不同的单位普通驾驶时间成本和单位迟到时间成本与单位早到时间成本之比下的最优停车策略选择的变化情况.单位普通驾驶时间成本增大,出行者会偏向于选择“早停迟到”策略,但影响很小. 图7 迟到/早到惩罚率-驾驶成本最优策略选择图 图8 迟到/早到惩罚率-驾驶成本的成本等高线图 图8给出了不同的单位普通驾驶时间成本和单位迟到时间成本与单位早到时间成本之比下的最小总成本的变化情况,单位普通驾驶时间成本越大,最小总成本越大. 图9中,给出了不同的单位寻位时间成本和单位迟到时间成本与单位早到时间成本之比下的最优停车策略选择的变化情况.由于单位寻位时间成本要高于普通驾驶过程中的单位时间成本并且低于步行过程中的单位时间成本,单位寻位时间成本α2从20元/h到25元/h.单位寻位时间成本不影响出行者的停车策略选择,验证了前文最优成本性质分析中的性质5. 图9 迟到/早到惩罚率-寻位成本最优策略选择图 图10给出了不同的单位寻位时间成本和单位迟到时间成本与单位早到时间成本之比下的最小总成本的变化情况,单位寻位时间成本越大,最小总成本越大. 图10 迟到/早到惩罚率-寻位成本的成本等高线 图11给出了不同的步行过程中的单位时间成本和单位迟到时间成本与单位早到时间成本之比下的最优停车策略选择的变化情况.由于步行过程中的单位时间成本要高于单位寻位时间成本,步行过程中的单位时间成本α3从25元/h到50元/h.单位步行时间成本增大,出行者会偏向于选择“早停早到”策略. 图11 迟到/早到惩罚率-步行成本最优策略选择图 图12是不同的步行过程中的单位时间成本和单位迟到时间成本与单位早到时间成本之比下的最小总成本的变化情况,可以看到单位步行时间成本越大,最小总成本越大. 图12 迟到/早到惩罚率-步行成本的成本等高线 图13给出了不同的单位时间停车收费和单位迟到时间成本与单位早到时间成本之比下的最优停车策略选择的变化情况.单位停车收费增高,出行者会偏向于选择“早停早到”策略. 图14是对应的最小总成本变化图,显然更高的停车收费会显著增加出行者的期望成本. 图13 迟到/早到惩罚率-停车收费最优策略选择图 图14 迟到/早到惩罚率-停车收费的成本等高线 本文依据出行者选择不同的提前找位距离和提前出发时间会导致出行者到达目的地延误的不同的可能状态,定义了“早停早到”、“早停迟到”、“不早到”三种停车策略.通过研究出行者在三种停车策略之间的决策,得到以下结论. 1)单位早到时间成本越低,单位迟到时间成本越高时,“早停早到”策略越可能成为最优策略;特别的,如果单位迟到时间成本小于单位早到时间成本,“早停迟到”策略一定是最优停车策略;“不早到”策略不可能成为最优选择. 2)如果最优策略是“早停早到”,则出行者将有50%以上概率在到达目的地前找到车位. 3)单位寻位时间成本不影响出行者的最优出行策略选择. 本文主要从出行者个人决策角度对寻位策略进行了研究,并没有考虑城市拥堵对出行者停车造成的干扰和影响.下一步的工作计划将拥堵纳入研究框架,从系统的角度对路边停车寻位车流对交通系统的影响进行分析,并研究相关拥堵的有效识别[20]. [1]张国伍. 停车系统在城市交通中的地位与作用[J]. 交通运输系统工程与信息, 2014, 14(1): 2-8. Zhang Guowu. The position and role of parking system in urban traffic[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(1): 2-8. (in Chinese) [2]Armonk N Y. IBM Global Parking Survey: Drivers Share Worldwide Parking Woes[R]. IBM News Room, 28 Sep 2011, http://www-03.ibm.com/press/us/en/pressrelease/35515.wss. [3]Glazer A, Niskanen E. Parking fees and congestion[J]. Regional Science and Urban Economics, 1992, 22(1): 123-132. [4]Arnott R, De Palma A, Lindsey R. A temporal and spatial equilibrium analysis of commuter parking[J]. Journal of Public Economics, 1992, 45(3): 301-335. [5]Verhoef E, Nijkamp P, Rietveld P. The economics of regulatory parking policies: The (im) possibilities of parking policies in traffic regulation[J]. Transportation Research Part A: Policy and Practice, 1995, 29(2): 141-156. [6]Arnott R, Rowse J. Downtown parking in auto city[J]. Regional Science and Urban Economics, 2009, 39(1): 1-14. [7]Button K. The political economy of parking charges in “first” and “second-best” worlds[J]. Transport Policy, 2006, 13(6): 470-478. [8]Calthrop E. Essays in urban transport economics [D]. Leuven: Catholic University of Leuven, 2001. [9]Calthrop E, Proost S. Regulating ton-street parking[J]. Regional Science and Urban Economics, 2006, 36(1): 29-48. [10]van Ommeren J, Wentink D, Dekkers J. The real price of parking policy[J]. Journal of Urban Economics, 2011, 70(1): 25-31. [11]van Ommeren J N, Wentink D, Rietveld P. Empirical evidence on cruising for parking[J]. Transportation Research Part A: Policy and Practice, 2012, 46(1): 123-130. [12]Kobus M B W, Gutiérrez-I-Puigarnau E, Rietveld P, et al. The on-street parking premium and car drivers’choice between street and garage parking[J]. Regional Science & Urban Economics, 2013, 43(2): 395-403. [13]Shoup D C. Cruisingfor parking[J]. Transport Policy, 2006, 13(6): 479-486. [14]徐红利, 周晶, 徐薇. 基于累积前景理论的随机网络用户均衡模型[J]. 管理科学学报, 2011, 14(7): 1-7, 54. Xu Hongli, Zhou Jing, Xu Wei. Cumulative prospect theory-based user equilibrium model for stochastic network[J]. Journal of Management Sciences in China, 2011, 14(7): 1-7, 54. (in Chinese) [15]田琼, 刘鹏. 基于乘客异质性的高峰期公交出行均衡研究[J]. 管理科学学报, 2013, 16(3): 82-87. Tian Qiong, Liu Peng. Equilibrium properties of peak-period commuting in mass transit system with heterogeneous passengers[J]. Journal of Management Sciences in China, 2013, 16(3): 82-87. (in Chinese) [16]田琼, 黄海军, 杨海. 瓶颈处停车换乘的Logit随机均衡选择模型[J]. 管理科学学报, 2005, 8(1): 1-6. Tian Qiong, Huang Haijun, Yang Hai. Mode choice models based on Logit stochastic equilibrium in transportation systems with park-and-ride option[J]. Journal of Management Sciences in China, 2005, 8(1): 1-6. (in Chinese) [17]Arnott R, de Palma A, Lindsey R. A structural model of peak-period congestion: A traffic bottleneck with elastic demand[J]. American Economic Review, 1993, 83: 161-179. [18]Arnott R, Rowse J. Modeling parking[J]. Journal of Urban Economics, 1999, 45(1): 97-124. [19]Arnott R, Rowse J. Downtown parking in auto city[J]. Regional Science and Urban Economics, 2009, 39(1): 1-14. [20]刘建美, 马寿峰, 贺正冰, 等. 控制与诱导的协调中路网拥堵状态识别方法[J]. 管理科学学报, 2010, 13(11): 35-40. Liu Jianmei, Ma Shoufeng, He Zhengbing, et al. Recognition method for congestion state of road network about coordination of traffic control and guidance[J]. Journal of Management Sciences in China, 2010, 13(11): 35-40. (in Chinese) The optimal curbside parking strategies with schedule delay TIANQiong,LUOTing,YANGLi School of Economics and Management, Beihang University, Beijing 100191, China This paper studies the effect of delay costs on the travelers’ parking strategy under the random distribution of curbside parking spaces. Travelers have to decide how long in advance they should depart to arrive at the destination and how far away from the destination they should start looking for an available parking space. Their costs include not only the ordinary travel costs, but also expected cruising costs and delay costs depending on the real-time distribution of curbside parking spaces. Then three parking strategies are defined according to their different possible states of the delays when traveler reaches his/her destination. The “never-early-arrival” strategy is proved to be irrational, while both the “early-park-early-arrival” strategy and the “early-park-late-arrival” strategy may be the optimal choice under different conditions. Typically, the “early-park-late-arrival” strategy is optimal if the unit time penalty of early arrival is no less than that of late arrival. Numerical results support the analytical propositions. curbside parking; schedule delay cost; parking strategy; cruising cost 2014-04-08; 2014-12-12. 国家自然科学基金资助项目(71071011; 71271017; 71471010); 国家973重大基础研究计划资助项目(2012CB725401). 田琼(1981—), 男, 河北廊坊人, 博士, 教授. Email: tianqiong@buaa.edu.cn F570; U491 A 1007-9807(2016)07-0050-10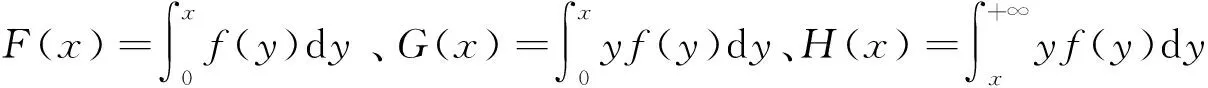
2 停车寻位策略




3 最优寻车策略分析
4 算 例







5 结束语
