带有能力约束的多元马氏需求报童模型
2016-09-02陈志祥邢灵博陈崇萍
陈 杰, 陈志祥, 邢灵博, 陈崇萍
(1. 中山大学管理学院, 广州 510275; 2. 海南热带海洋学院数学系, 三亚 572022)
带有能力约束的多元马氏需求报童模型
陈杰1, 2, 陈志祥1, 邢灵博2, 陈崇萍1
(1. 中山大学管理学院, 广州 510275; 2. 海南热带海洋学院数学系, 三亚 572022)
在随机需求环境下考虑带有能力约束的多产品报童问题.为了对多产品的需求进行预测,并度量其需求间的关系,本文首先建立了多元马氏需求模型.其次,在该模型的理论基础上,提出了带有能力约束的多元马氏需求报童模型,进而给出多产品的最优订购策略解.最后,利用期望需求状态的概率值及其截尾概率分析了模型最优解的性质.模型的结论表明,在能力约束的条件下,最优订购量关于左截尾概率单调递减,关于右截尾概率单调递增,而期望需求状态的概率值对最优订购量具有双重的特殊影响.
多元马氏链; 多产品报童模型; 能力约束; 截尾概率; 最优订购策略
0 引 言
Whitin[1]是较早研究报童模型的学者之一,他提出的模型在库存优化管理领域里得到了空前的应用和拓展,但随着现代供应链管理所提倡的具有革命性的QRD(quickly respond to demand)理念的提出[2],经典报童模型的整个理论体系受到了极大的冲击和挑战.QRD供应理念要求供应商对市场的需求做出迅速的响应,这种响应方式建立在正确的订购策略基础之上,并以需求预测为前提条件,这对需求的预测提出了更高的要求.然而,在能力约束的条件下,以需求预测为基础的经典报童模型[3],得出来的最优订购策略存在不足之处,即在给定需求的分布函数的条件下,最优订购策略只跟能力、单位缺货成本和过剩费用等非随机因素有关,该模型忽略了需求状态的概率值及其左、右截尾概率对模型最优解的影响.同样,在处理多产品的最优化问题时,传统的多产品报童模型也忽略了各产品需求间的关联性.因此,在随机需求环境下,其模型的理论设计有待于进一步完善.
近年来,报童模型作为优化库存订购决策的重要理论工具,仍是理论研究的热点之一.姚忠[4]在风险约束下运用报童库存模型建立了供应链决策模型,分析了退货策略对单周期供应链的协调性.黄松等[5,6]则考虑了战略顾客行为因素并引入了理性预期均衡分析,建立了相应的模型并得到战略顾客双方静态博弈时的理性预计均衡解.李毅学等[7]考虑了统一授信模式的特征及成本收益结构,借鉴贸易融资中“主体+债项”的风险评估思路,构建融资约束下的报童模型,分析风险中性的借款企业的再订购决策,并通过借款企业和物流企业的Stackelberg动态博弈,分析下侧风险规避的物流企业的质押率决策.谷水亮和鞠彦兵[8]结合资金因素建立了多产品的报童模型,并通过费用函数最小化的实现来寻求满足约束条件的最优订购量.朱赛花等[9]研究了在资源和预算约束条件下允许外购的多产品报童问题,在非零延迟时间外购情况下建立了以求总体花费最小值为目标函数的优化模型.周艳菊等[10]考虑了需求不确定条件下的两产品订货问题,在前景理论的框架下分析、推导了随机市场需求下零售商对两产品订货的价值函数、主观概率与决策权重函数,并建立了两产品报童的订货模型.Chen[11]在资源约束的条件下,研究了报童问题的Stackelberg-Nash均衡策略,并从理论上证明了其存在性和唯一性.在风险约束条件下,Choi和Ruszczyński[12]利用指数效函数对多产品报童模型的风险规避性进行了系统的分析.基于预算约束的条件,Shi和Zhang[13]联合定价和折扣因子提出了多产品报童模型.Zhang和Du[14]在能力的约束条件和假设不同产品的需求相互独立的情况下,引入产品外包的思想考虑了报童问题,并给出模型的最优解及其性质.在服务和损失约束条件下,Jammernegg和Kischka[15,16]研究了风险偏好及价格敏感下的报童模型.Murray等[17]在资源能力约束的条件下,建立了基于价格敏感的多产品报童模型,并利用整数规划方法给出模型的最优解.由于带约束条件的多产品报童模型求解过程比较复杂,从而引起一些学者致力于对其求解方法的研究.Zhang和Hua[18]通过组合方法对带有预算约束条件的多产品模型进行求解,而Abdel和Otegbeye[19]则利用可分离规划和对偶方法对相应模型的求解方法进行研究.虽然以上对多产品报童模型的研究成果进一步完善了报童模型的理论,但是这些理论成果有个共同点就是基于各产品需求间的独立性.然而,在随机需求的环境下,由于顾客的需求具有多样性、偏好性和转移性等显著特点,导致多产品的需求之间发生相互转移, 从而产生需求间的关联性.显然,在这种情形下各产品的需求间不具有独立性.因此,需进一步发展新的理论工具来解决此类库存优化问题.
Ching等[20]在传统马氏理论的基础上提出了更一般化的马氏链,即多元马尔可夫模型,并建立了多产品的需求状态预测模型.虽然利用多元马尔可夫模型可以解决多产品需求状态间的关系和需求状态预测问题,但需求状态毕竟不是需求量,两者是不同的概念.现代库存优化控制理论基本上都是以需求量的预测为基础,而不是需求状态,因此该模型的理论成果与经典报童模型不具有兼容性.事实上, 所谓需求状态就是决策者根据产品需求量的大小对其进行等级划分,如实践过程中常将其划分为淡季、一般、中等、较好和旺季等五个需求状态(具体的定义详见文献[21]的第6.3.2节).可见,需求状态和需求量具有属性之别,即前者为产品需求的定性描述,而后者则为定量描述.Ching等提出的预测模型只给出产品的需求在未来的某个周期所处的状态,如处于淡季或旺季状态,即只给出模糊的需求程度,却未指出产品未来的具体需求量.经典报童模型则建立在随机需求变量x的密度函数f(x)的基础之上,其中变量x表示产品的需求量,而非需求状态.因此,两者不具有兼容性.为了克服这个技术难点,本文首先将需求量进行状态划分作为理论的切入点,再利用需求量的密度函数作为状态依赖的假设条件,转化期望需求状态为期望需求量,进而在建立多元马氏需求模型的理论基础上,提出带有能力约束的多元马氏需求报童模型,并基于该模型研究多产品的最优订购策略问题.同时,利用期望需求状态的概率值及其截尾概率分析该模型最优解的性质.
1 模型构建
1.1模型描述、符号说明和假设
需求的多样性、转移性是现代消费最显著的特性之一,消费者在产品的品牌、质量、价格和实用性等诸多方面具有不同的需求偏好性.供应商为了顺应这种趋势以保持其在市场竞争中的优势,往往致力于沿着商品的多元化方向进行研发和拓展.在这样的市场环境下,当消费者面临多种选择时,在一定的时间段有可能因为选择了A系列产品,而不会再选择其它系列的产品,或者在某个时期内选择A产品,而在下个阶段选择消费B产品,从而导致顾客需求在不同产品间发生转移.可见,需求转移是消费市场客观存在的一种普遍的经济现象.在能力约束条件下,当多种产品的顾客需求在不同产品之间产生相互转移时,如何科学地度量它们之间的关系并预测其需求,直接影响到库存系统决策者所制定的库存订购策略的科学性和合理性.因此,库存决策者为了达到优化库存的目的,不但要考虑各产品的需求,在宏观上还要确定各产品需求间的关系.为了方便问题的阐述,首先作出以下符号的说明
k=1,2,…,K表示库存系统的周期,而n=1,…,N表示第n种产品;
I={i1,i2,…,il}表示各产品的需求状态集;
dnk∈I为第n种产品在第k周期的需求状态,k=1,2,…,K;
{dnk}=带有l×l-转移概率矩阵P(nn)=(pji)l×l的第n条马氏链;
Dnk=第n种产品在第k周期的需求量,其中Dnk≥0;
P(ji)=第i种产品的需求状态到第j种产品的需求状态的转移概率矩阵;

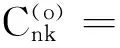
wnk=第k周期内生产第n种产品的单位资源消耗量;
Qnk=第n种产品在第k周期的订购批量;
SLnk=第n种产品在第k周期的最优服务水平;

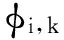
1.2多元马氏需求模型
需求预测是现代库存优化控制理论的基础,如何对产品的需求做出科学的预测关乎库存优化决策的科学性和合理性.本文主要以多元马尔可夫理论方法对多产品的需求进行统一预测,进而确定它们之间的关系.为了建立多元马氏需求模型,首先介绍以下引理.
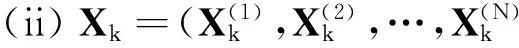
证毕.
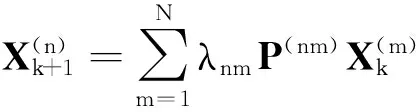

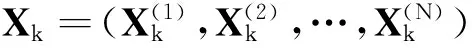
(1)
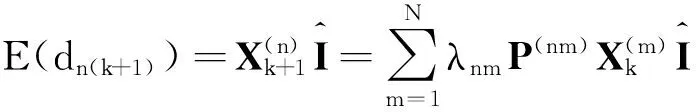

it
(2)
同时,称a为需求状态分类系数,而称[(t-1)a,ta)为隶属于状态it的需求区间.
以上的式子通过映射f(·)给出了需求量转化为需求状态的一般方法,接下来主要研究如何将需求状态转化为需求量.由式(2)和模型的假设1可知Dnk为状态依赖的,故可设φit,k(Dnk)为当dnk=it时的密度函数,即φit,k(Dnk)为当Dnk属于区间[(t-1)a,ta)时的概率密度.于是,可得出以下命题.


(3)
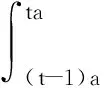
证毕.
命题2的结论不但确定了变量dnk和Dnk之间的关系,还给出了将dnk转化为Dnk的具体方法.该结论在研究马氏理论在库存问题的应用中是至关重要的.因为多元马氏链是根据需求状态的转移概率对系统未来所处的需求状态作出科学预测,所以得到的预测结果是需求状态而非需求量.有了命题2的理论基础,接下来即可建立多产品的多元马氏需求模型.
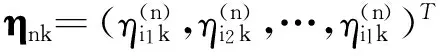
E(Dk+1)=Xk+1ηk+1=AXkηk+1
(4)
这里A和Xk如引理1所定义,而Dk+1=(D1(k+1),D2(k+1),…,DN(k+1))T,称式(4)为多元马氏需求模型.
由该模型,易知第n种产品于第k+1周期的期望需求量为
(5)
E(Dn(k+1))的表达式,进一步表明了单个产品在下个周期的需求量不但与现阶段相关,还与其它产品的需求量有着密切的关联,它们之间的关系权数同样为λnm.
1.3带有能力约束的多元马氏需求报童模型
在假设φ(x)为随机需求x的概率密度条件下,经典的报童模型为[3]
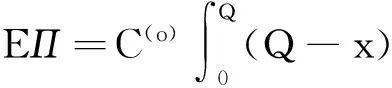

(6)
其中C(s)和C(o)分别为产品的单位缺货成本和单位过剩成本,Q为产品的订购量.本小节主要在经典的报童模型的理论基础上,结合上文提出的多元马氏需求模型,在能力约束条件下研究建立新的多产品报童模型.
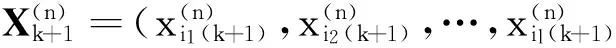
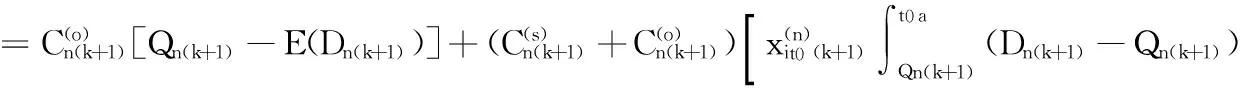
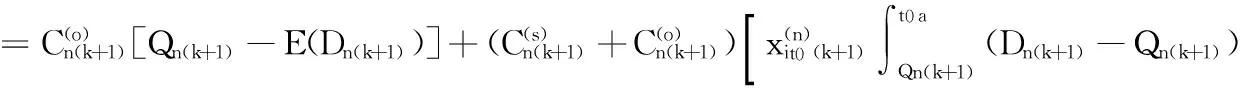
(7)


若记EΠ=V(Q1(k+1),Q2(k+1),…,QN(k+1))为销售商的总期望成本,在模型的各个假设条件下结合式(7),则有
EΠ=V(Q1(k+1),Q2(k+1),…,QN(k+1))
(8)
记wnk为在第k周期内生产第n种产品所消耗的单位资源量,C为总产品在生产过程中能获取资源的能力上限.于是,在相应的能力约束的条件下,结合式(8)即可提出以下的(MP)问题,即带有能力约束的多元马氏需求报童模型
(9)
由式(9)可知,多产品报童模型EΠ是关于订购量Q1(k+1),Q2(k+1),…,QN(k+1)的函数.因此,只需利用多元马氏理论求出各产品的期望需求E(Dn(k+1))的值,再确定Qn(k+1)的最优值,即可达到优化订购策略的目的.
2 模型的最优解及其性质
2.1模型的最优订货策略
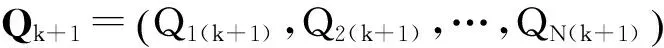
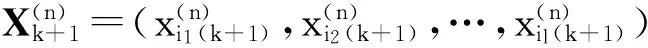
(10)
这里λ*为模型(9)的Kuhn-Tucker条件的拉格朗日乘子.
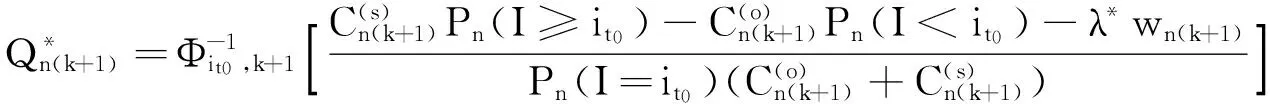

证毕.

(11)
2.2最优解的性质
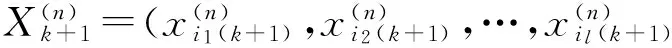
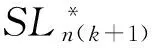
证毕.

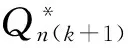
证明由
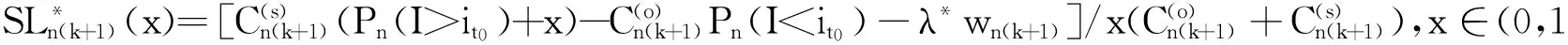

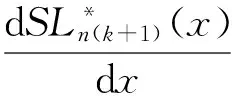
证毕.

3 数值算例分析
限于篇幅,本算例只考虑3种产品的情形.设某零售商销售A、B、C三种产品,根据消费者对产品的需求程度将其划分为4个状态,依次用数值1,2,3,4表示,即状态集I={1,2,3,4},其中各需求状态的定义如下
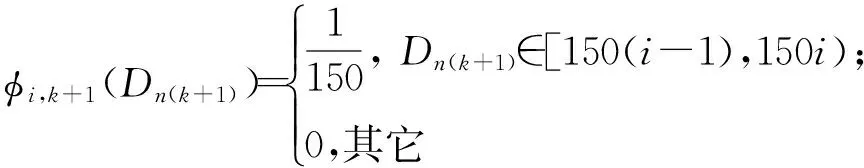
则由式(4)中对ηk+1的定义可得ηn(k+1)=(75,225,375,525)T,n=1,2,3.
3.1期望需求量和左右截尾概率
若A、B、C三种产品在以往12个周期的需求状态历史数据分别为:H1={4,3,1,3,4,4,3,3,1,2,3,4},H2={1,2,3,4,1,4,4,3,3,1,3,1}和H3={2,1,3,3,2,4,2,3,4,1,4,3},且其需求状态间相互转移的关系如图1所示

图1不同产品间需求状态转移图示


根据图1中不同产品间需求状态的转移规律,可得各产品需求状态的转移频数和概率矩阵

其中F(ji)表示从第i种产品的需求状态到第j种产品的需求状态的转移频数矩阵,P(ji)表示从第i种产品的需求状态到第j种产品的需求状态的转移概率矩阵(其具体的定义和求解方法详见文献[21]的第7章).
基于A、B、C三种产品需求状态的历史周期数据,易估计出它们的需求状态的平稳分布
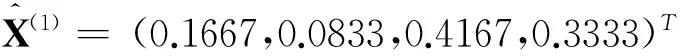
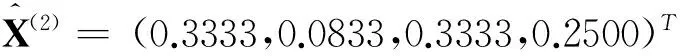




表1 A, B, C产品于第k+1周期需求状态I和期望需求量ηn(k+1)的概率分布
再由式(4),可得A、B和C产品于第k+1周期的期望需求量,即
因此,根据本算例给出的需求状态的定义,知E(Dn(k+1))∈[300,450),n=1,2,3,故A、B、C三种产品在下个周期所处的期望需求状态都为E(dn(k+1))=3,进而可得各产品在下个周期处于期望需求状态3的概率值分别为:P1(I=3)=0.633,P2(I=3)=0.300和P3(I=3)=0.133;其左截尾概率分别为:P1(I<3)=0.033,P2(I<3)=0.334和P3(I<3)=0.501;右截尾概率分别为:P1(I≥3)=0.966,P2(I≥3)=0.667和P3(I≥3)=0.500.
3.2模型的最优数值解及其分析
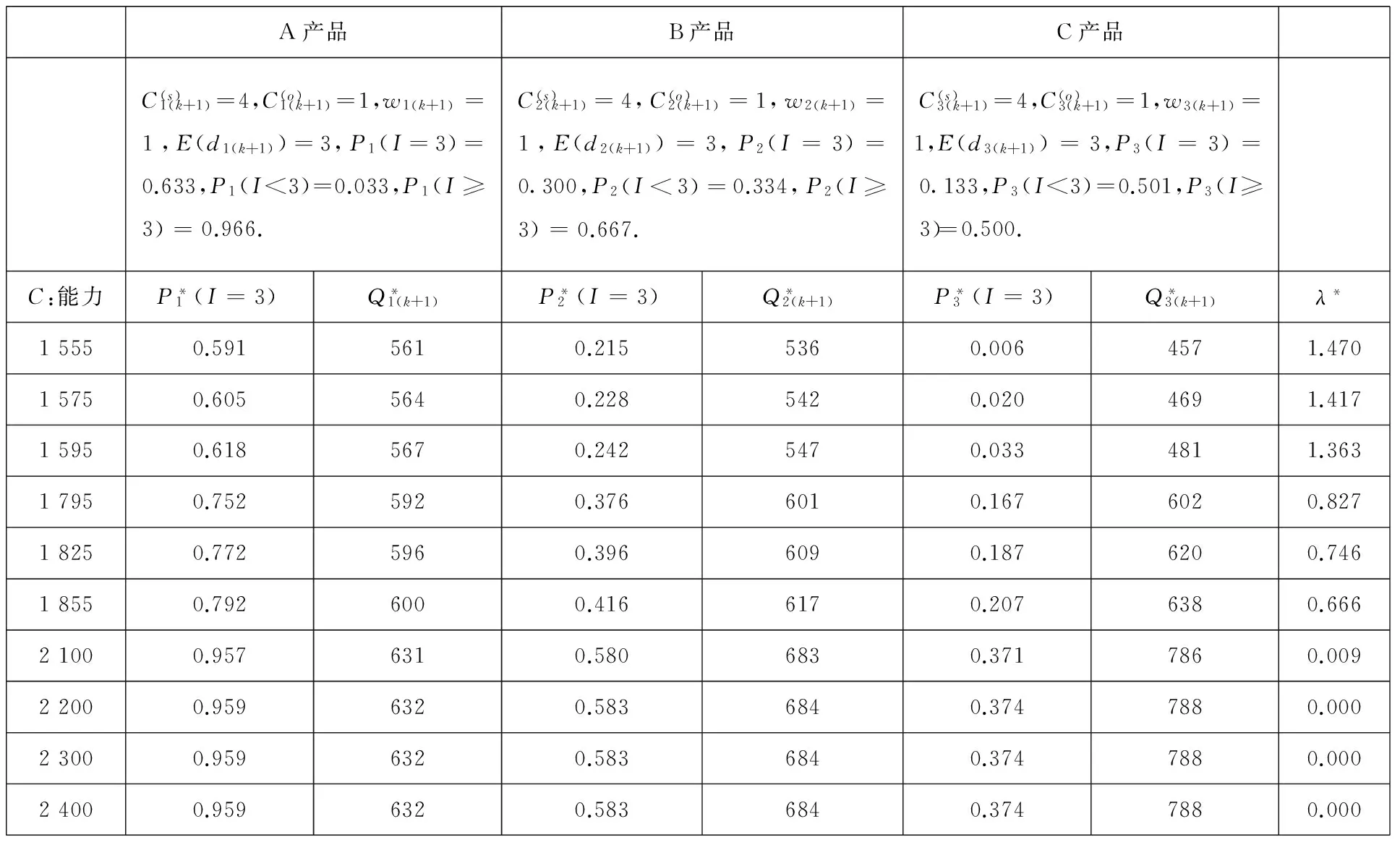
表2 能力(capacity)约束下Pn(I=3)的临界值及其相应的模型最优解(n=1,2,3)


图2 能力约束C对最优订购量的影响
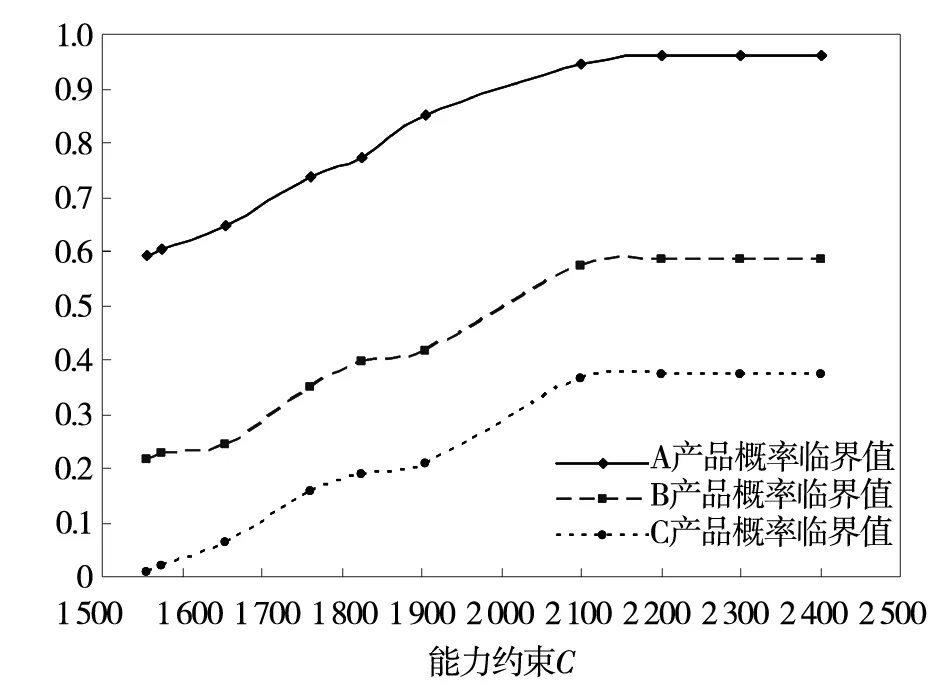
图3 能力约束C对概率临界值的影响

4 结束语

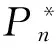
[1]Whitin T M. Inventory control and price theory[J]. Management Science, 1955, 2(1): 61-68.
[2]Bisi A, Dada M. Dynamic learning, pricing, and ordering by a censored newsvendor[J]. Naval Research Logistics (NRL), 2007, 54(4): 448-461.
[3]Lau H S, Hing-Ling Lau A. The newsstand problem: A capacitated multiple-product single-period inventory problem[J]. European Journal of Operational Research, 1996, 94(1): 29-42.
[4]姚忠. 风险约束下退货合同对供应链的协调性分析[J]. 管理科学学报, 2008, 11(3): 96-105.
Yao Zhong. Analysis of return policy for coordinating supply chain under downside risk constraints[J]. Journal of Management Sciences in China, 2008, 11(3): 96-105. (in Chinese)
[5]黄松, 杨超, 张曦. 考虑战略顾客行为带预算约束的多产品报童问题[J]. 中国管理科学, 2011, 19(3): 70-78.
Huang Song, Yang Chao, Zhang Xi. Multi-product newsvendor problem with budget constraint and strategic customers[J]. Chinese Journal of Management Science, 2011, 19(3): 70-78. (in Chinese)
[6]黄松, 杨超, 张曦. 考虑战略顾客行为时的供应链性能分析与协调[J]. 管理科学学报, 2012, 15(2): 47-58.
Huang Song, Yang Chao, Zhang Xi. Supply chain performance analysis and coordination with consideration of strategic customer behavior[J]. Journal of Management Sciences in China, 2012, 15(2): 47-58. (in Chinese)
[7]李毅学, 汪寿阳, 冯耕中. 物流金融中季节性存货质押融资质押率决策[J]. 管理科学学报, 2011, 14(11): 19-32.
Li Yixue, Wang Shouyang, Feng Gengzhong. Decision of loon-to-calue katios of seasonal inventon/pledge financing based on logistics finance[J]. Journal of Management Sciences in China, 2011, 14(11): 19-32. (in Chinese)
[8]谷水亮, 鞠彦兵. 资金和风险约束下的多产品报童模型最优解的研究[J]. 软科学, 2012, 26(3): 129-133.
Gu Shuiliang, Ju Yanbing. The study of the optimal solution of multi-product newsvendor in the constraints of funding and risk[J]. Soft Science, 2012, 26(3): 129-133. (in Chinese)
[9]朱赛花, 戴琳, 胡朝明. 两个约束条件下允许外购的多产品报童问题[J]. 经济数学, 2013, 30(2): 31-35.
Zhu Saihua, Dai Lin, Hu Zhaoming. Multi-product newsboy problem with two constraints and nonzero lead time outsourcing[J]. Journal of Quantitative Economics, 2013, 30(2): 31-35. (in Chinese)
[10]周艳菊, 应仁仁, 陈晓红, 等. 基于前景理论的两产品报童的订货模型[J]. 管理科学学报, 2013, 16(11): 17-29.
Zhou Yanju, Ying Renren, Chen Xiaohong, et al. Two product newsboy problem based on prospect theory[J]. Journal of Management Sciences in China, 2013, 16(11): 17-29. (in Chinese)
[11]Chen Y J. Existence and uniqueness of Nash equilibrium in a supply chain newsvendor game[J]. Journal of Nonlinear Analysis and Optimization: Theory & Applications, 2011, 2(1): 20-28.
[12]Choi S, Ruszczyński A. A multi-product risk-averse newsvendor with exponential utility function[J]. European Journal of Operational Research, 2011, 214(1): 78-84.
[13]Shi J, Zhang G. Multi-product budget-constrained acquisition and pricing with uncertain demand and supplier quantity discounts[J]. International Journal of Production Economics, 2010, 128(1): 322-331.
[14]Zhang B, Du S. Multi-product newsboy problem with limited capacity and outsourcing[J]. European Journal of Operational Research, 2010, 202(1): 107-113.
[15]Jammernegg W, Kischka P. Risk preferences of a newsvendor with service and loss constraints[J]. International Journal of Production Economics, 2013, 143(2): 410-415.
[16]Jammernegg W, Kischka P. The price-setting newsvendor with service and loss constraints[J]. Omega, 2013, 41(2): 326-335.
[17]Murray C C, Gosavi A, Talukdar D. The multi-product price-setting newsvendor with resource capacity constraints[J]. International Journal of Production Economics, 2012, 138(1): 148-158.
[18]Zhang B, Hua Z. A portfolio approach to multi-product newsboy problem with budget constraint[J]. Computers & Industrial Engineering, 2010, 58(4): 759-765.
[19]Abdel-Malek L L, Otegbeye M. Separable programming/duality approach to solving the multi-product newsboy/gardener problem with linear constraints[J]. Applied Mathematical Modeling, 2013, 37(10): 4497-4508.
[20]Ching W K, Fung E S, Ng M K. A multivariate Markov chain model for categorical data sequences and its applications in demand predictions[J]. IMA Journal of Management Mathematics, 2002, 13(3): 187-199.
[21]Ching W K, Ng M K. Markov Chains: Models, Algorithms and Applications[M]. New York: Springer, 2006.
Capacitated newsboy model with multivariate Markovian demand
CHENJie1, 2,CHENZhi-xiang1,XINGLing-bo2,CHENChong-ping1
1. School of Business, Sun Yat-sen University, Guangzhou 510275, China;2. Department of Mathematics, Hainan Tropical Ocean University, Sanya 572022, China
In this paper, a multi-product capacitated newsvendor model with stochastic demand is studied. Firstly, a multivariate Markovian demand model to forecast the demands of multiple products is constructed, and the relationships among the demands are measured by the model. Secondly, a capacitated newsboy model with multivariate Markovian demand is proposed, and then the solution of optimal ordering policy for multiple products is derived. At last, the properties of the optimal policy through the probability value and truncated probability of the expected demand state are discussed. With capacity constrains, the theoretical analysis shows that the optimal ordering quantity is a monotonic decreasing function with respect to the left truncated probability, and a monotonic increasing function with respect to the right truncated probability, but the probability value of the expected demand state has special dual effects on the optimal ordering quantity.
multivariate Markov chains; multi-product newsboy problem; capacity constraint; truncated probability; optimal ordering policy
2014-01-08;
2015-02-19.
国家自然科学基金资助项目(71372154); 海南省自然科学基金资助项目(20151008); 教育部人文社会科学研究青年基金资助项目(15YJC630013).
陈杰(1979—), 男, 海南临高人, 博士, 副教授. Email: sysuchenjie@126.com
O211.62; F253.4
A
1007-9807(2016)07-0037-13
