动载荷施加方式对船舶设备—基座系统建模方法的影响

郁扬，杨德庆，刘见华，石嘉欣

1上海交通大学海洋工程国家重点实验室，上海2002402高新船舶与深海开发装备协同创新中心，上海2002403中国船舶及海洋工程设计研究院，上海200011

动载荷施加方式对船舶设备—基座系统建模方法的影响

郁扬1，2，杨德庆1，2，刘见华3，石嘉欣1，2

1上海交通大学海洋工程国家重点实验室，上海200240
2高新船舶与深海开发装备协同创新中心，上海200240
3中国船舶及海洋工程设计研究院，上海200011

船舶结构动力响应分析中，设备动载荷是通过基座传递到船体板架上的，构成了设备—基座系统。由于设备激振力较难测量，而设备传递到基座面板处的加速度容易测量，因此在实际工程中，按设备力载荷施加与按基座面板传递加速度载荷施加时，针对船体结构动力学响应的等效性研究，以及相关建模方法研究具有重要的应用价值。通过理论推导，分析2种动载荷施加方式对模型建立方法的影响；并针对某实船特定舱段，建立有限元模型，通过比较在设备—基座模型中施加激振力载荷与在单基座模型中施加加速度载荷2种情况下评价点的振动加速度级，验证结论的正确性。研究表明，在低频域内，载荷以加速度输入时，在设备—基座系统的有限元模型中无需考虑设备建模及其质量分布。

动载荷；设备—基座系统；等效性；加速度

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.026.html期刊网址：www.ship-research.com

引用格式：郁扬，杨德庆，刘见华，等.动载荷施加方式对船舶设备—基座系统建模方法的影响［J］.中国舰船研究，2016，11（4）：93-101.

YU Yang，YANG Deqing，LIU Jianhua，et al.The influence of dynamic loads on the FE model of the ship equipment-base system［J］.Chinese Journal of Ship Research，2016，11（4）：93-101.

0　引　言

在船舶结构动力学响应分析中，设备动载荷是主要的振源。设备动载荷通过设备—基座系统传递到船体板架上。在建模过程中，若按照实际情况详尽模拟，则需要知道设备的动力学参数、隔振器的刚度和阻尼系数等，以及设备的激振力数据。由于激振力较难测量，且设备详细模拟建模耗时过长，因此，对于整艘船建模而言，实际操作性不强。但是，设备通过隔振器传递到基座的振动加速度容易测量，所以有必要研究以加速度载荷输入和以激振力载荷输入的振动响应的等效性及其对有限元模型建立方式的影响，从而准确计算结构振动响应［1-3］。国内外的研究大多针对激振力作用下结构的动力学响应情况，采用的方法有解析法、有限元法、边界元法和统计能量法等［4-6］。目前计算船体振动噪声时，对于设备—基座系统的建模方式一直存在误区，应该如何根据不同种类的外载荷建立设备—基座系统的有限元模型尚无定论。因此，本文将得出的结论会对实际工程具有重要的参考价值。

本文拟针对低频区域，首先将设备—基座系统简化为质点系统，通过理论分析和公式推导得出质点系统中动载荷施加方式与质点系模型建立方式之间的关系，得出以加速度方式施加载荷和以激振力方式施加载荷2种不同模型之间的等效性规律。之后，为了验证质点系统中得到的规律能否推广到连续系统中，将通过软件MSC/Patran建立连续体有限元模型，分析基座在几种不同建模方式下系统结构动力响应的情况，得出连续体模型与实际结构的等效性规律［7-9］。并将在此基础上，建立不同隔振器刚度的数值模型，验证规律的一般性。

1　质点简化系统中动力响应等效性

图1所示的2个系统分别代表双自由度的设备—基座系统以及与之等效的单自由度基座系统的简化模型。在图1（a）的设备—基座双自由度系统中，外加动载荷为激振力F=F0ejωt（其中j为虚数单位，ω为圆频率），设备质量为M1，设备与基座相连的隔振器弹簧刚度为K1，阻尼为C1（二者共同组成设备—隔振器质点系）；基座质量为M2，基座与船体板架连接刚度为K2，阻尼为C2（二者共同表示基座的隔振效应）。在图1（b）的基座单自由度模型中，外加动载荷为加速度ẍ2=-ω2Q2ejωt，此时已省略设备以及设备与基座相连的弹簧和阻尼。基座质量为M2，基座与船体板架相连的弹簧刚度为K2，阻尼器阻尼为C2。

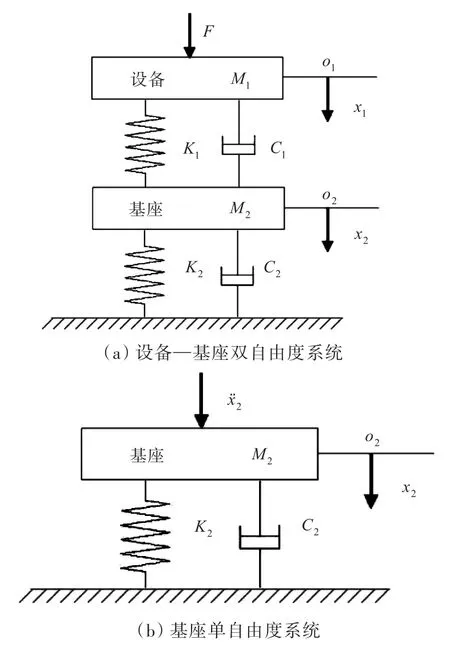
图1　基座简化的两种质点系模型示意图Fig.1　Diagram of simplified equipment-base system

这种简化实际上是把设备和基座这2个连续体简化为质点与阻尼弹簧这种质点系模型（图2），将不易分析的连续系统变为可以用公式推导的质点系统［10］。在这种模型下，研究不同外载荷输入下的等效性问题更加简单、方便。

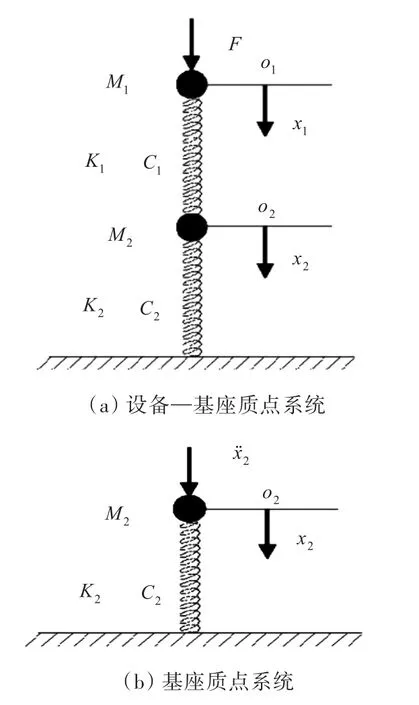
图2　基座简化的等价质点系模型Fig.2　Equivalent particle system model of equipment-base system

在图1（a）所示设备—基座系统中，激振力F=F0ejωt作用于设备 M1，利用观察法写出系统动力学方程为

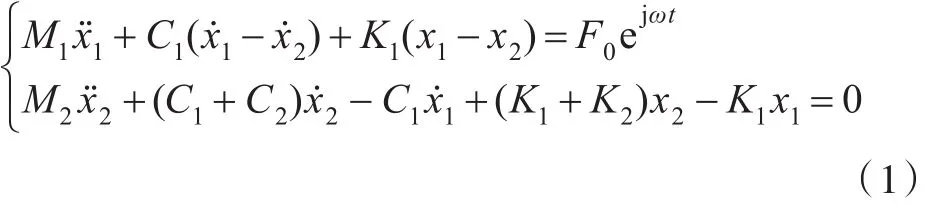
解得图1（a）中系统的位移响应为

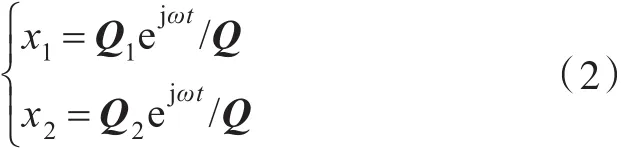
式中：

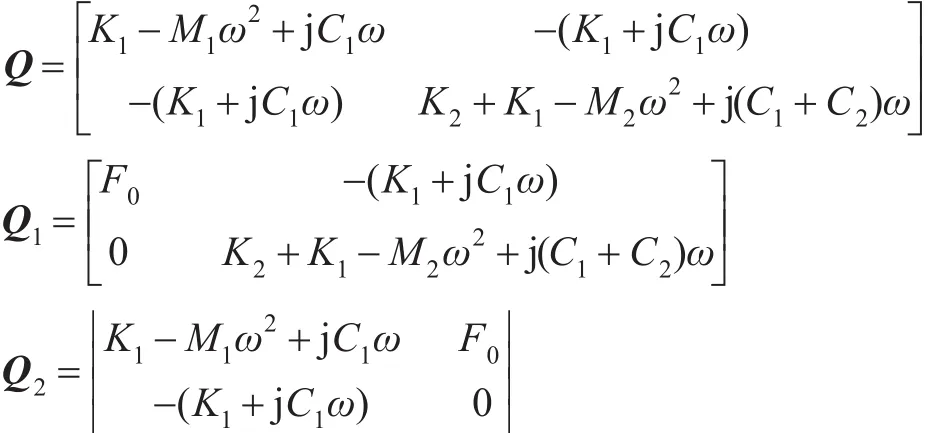
图1（a）系统中，将设备M1与基座M2之间的作用力视为基座所受的等效外力，则该外力可表示为

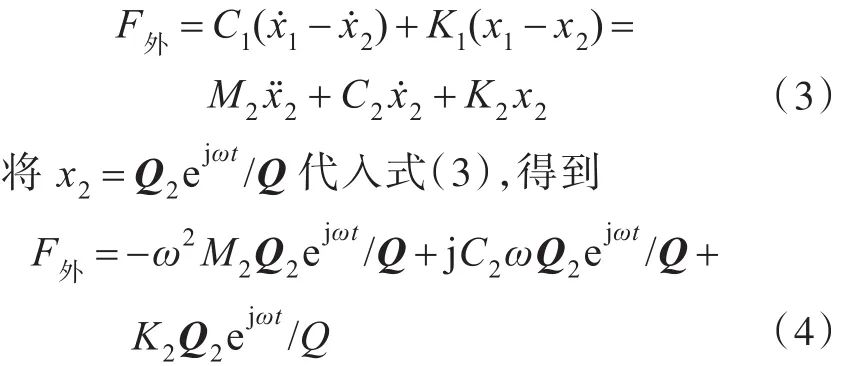
对于图1（b）所示的基座系统，其动力学方程为

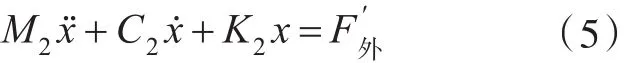
式（5）可改写为

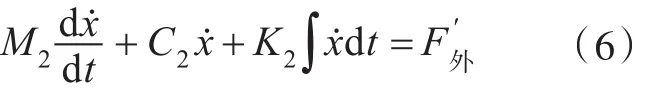
求解式（6），得到外力与速度的关系为

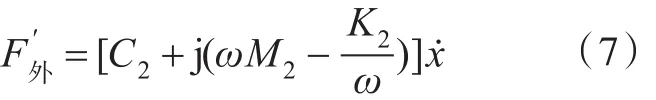
基座受到的加速度外载荷为 ẍ=ẍ2= -ω2Q2ejωt/Q，代入到式（7），得

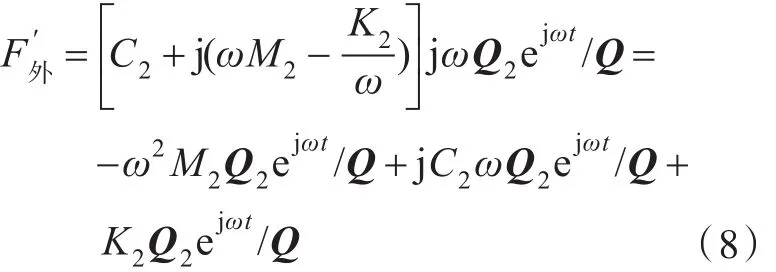
对比上述推导中的式（4）与式（8），将图1（a）中设备与基座之间的作用力视为基座所受到的激振力外力，并将图1（b）中加速度外载荷转化为等效虚拟外力。经对比可知，图1（a）中基座所受到的激振力外力与图1（b）中的等效虚拟外力相等。

上述公式推导结果表明：

1）以激振力为输入量的外载荷可以转换为等效的加速度外载荷或速度外载荷。

2）在图1（a）的设备—基座双自由度系统中施加激振力外载荷的系统动力学响应等效于简化为图1（b）基座单自由度系统中施加相应的加速度外载荷的系统动力学响应。从图1（a）模型简化为图1（b）模型，必须去掉图1（a）的设备质量以及隔振器，两者响应才能等效。

上述结论是将设备—基座连续系统简化为质点系统后所得到的，在下节中将通过数值实验证明该结论同样可以应用于连续系统。

2　连续系统中动力响应等效性

上节推导了设备—基座质点系模型中载荷等效性公式，使设备—基座双自由度系统中施加激振力外载荷等效于在基座单自由度系统中施加相应的加速度外载荷。推导是基于质点系简化模型，能否推广到连续系统中还有待验证。下面将通过有限元方法来验证实际结构中设备—基座连续系统简化为基座连续系统是否仍需去除设备质量以及隔振器。为此，本文将建立4种设备—基座连续模型，验证上述等效方法及模型简化方法。

2.14种设备—基座连续系统有限元模型

图3所示为用MSC/Patran软件建立的某双体船下潜体舱段有限元模型。该舱段部分为双层底结构，内底板上有一设备—基座系统。在该有限元模型中，设备采用实体单元模拟，重量为29 t；设备下隔振器采用Spring单元模拟，弹簧弹性系数K=2 000 N/mm，阻尼系数C=0.5；基座与船体板架采用Shell单元模拟，船体板架横梁以及加强筋采用Beam单元模拟。该模型共1 754个单元，1 205个节点，总重量为50 t。舱段左、右均为简支约束，即只约束X，Y，Z这3个方向的平动自由度，不约束扭转自由度。在该设备—基座系统中，单层隔振装置的隔振器数量为10个，基座面板上方左右各5个，设备加载方式为激振力F=1 000 N，频率范围为0～100 Hz，加载位置为设备质心处［11］。此模型模拟设备—基座连续系统，对应于简化为图1（a）的双自由度设备—基座系统模型，称之为原始模型。

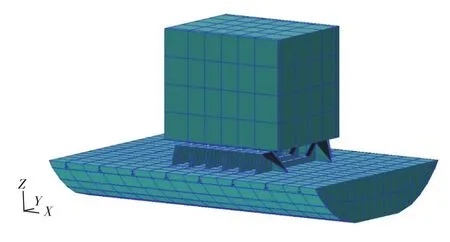
图3　原始模型Fig.3　Original model

将原始模型的设备与隔振器删除后，在原机脚位置施加速度外载荷，所得新模型对应于简化为图1（b）的单自由度基座系统模型，称之为单基座模型，如图4所示。为对比说明前述结论的正确性，同时建立了另外2个模型，这2个模型采用的也是施加加速度外载荷常见的建模方式。如图5所示：其一是将均布质量点添加到模型基座下方船体板架区域，用来代替去掉设备后所损失的质量，质量点不偏心，称此模型为无偏心质量点模型；其二是将无偏心质量点模型中质量点偏心，使其重心位于设备质心处，称此模型为偏心质量点模型。

图4　单基座模型Fig.4　Single-base model

图5　质量点模型Fig.5　Mass-point model

4个模型中，都在相同的位置设置了6个评价点，评价点的位置分别为中纵剖面与内底板交线上中心处、基座边缘处、远离基座处，以及基座腹板与内底板交线上中心处、基座边缘处、远离基座处。具体位置如图6所示。

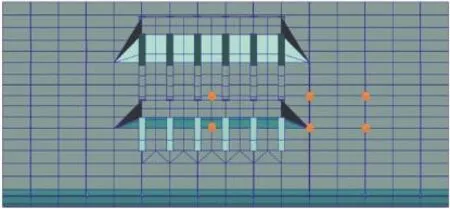
图6　评价点位置Fig.6　Location of check points

2.2不同模型动力学响应计算结果及分析

原始模型中，在设备质心处施加F=1 000 N、频率范围为0～100 Hz的激振力。通过频率响应分析，用直接法求解，计算出一侧基座面板上设备传递到基座面板处的5组加速度，以及6个评价点处的加速度。5组加速度转化为加速度级后按顺序列出，如表1所示。

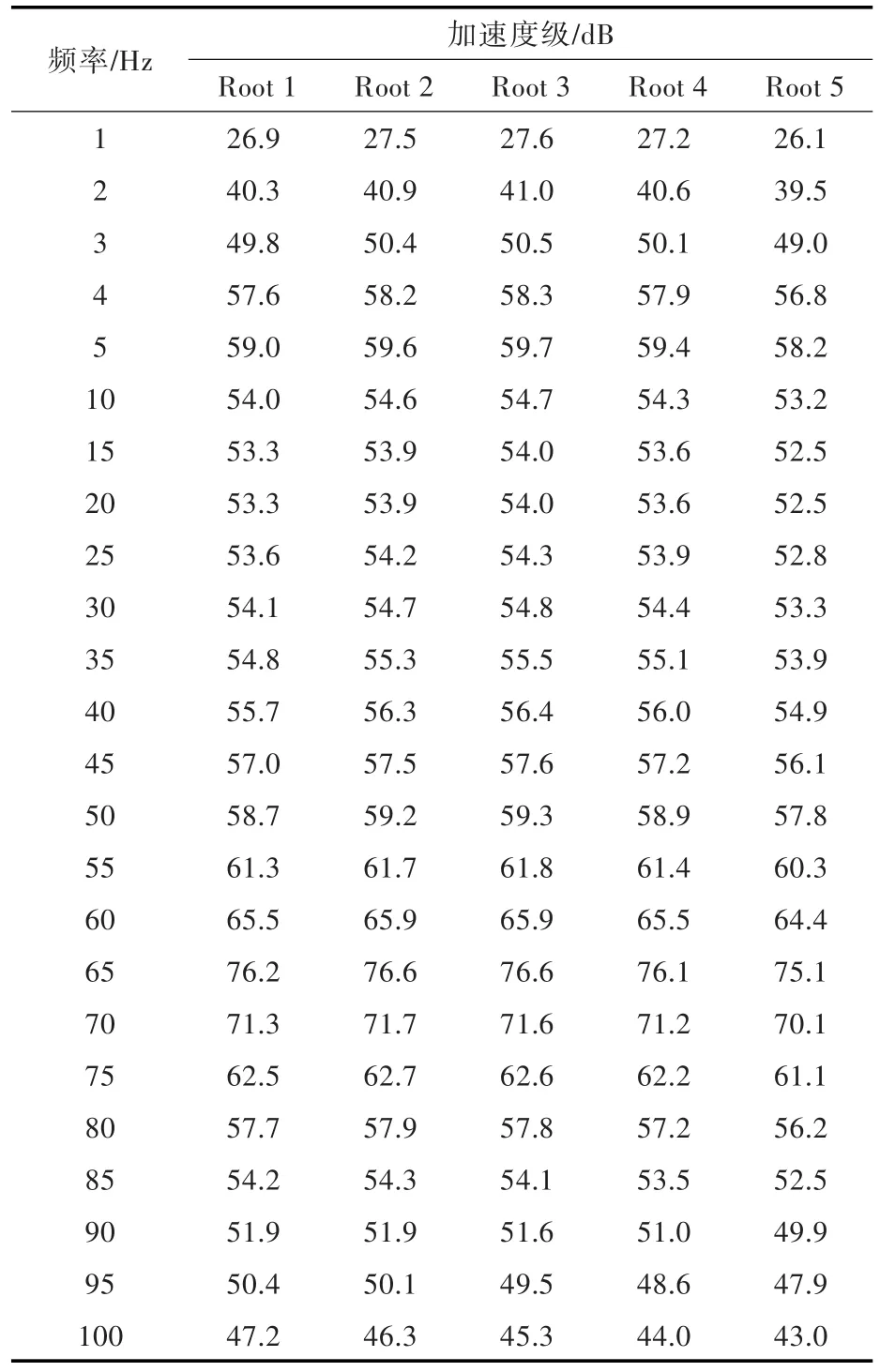
表1　原始模型设备传递到基座面板处加速度级Tab.1　Base panel acceleration level of the original model

分析表1数据，可以得出，5个点的加速度级基本上为对称分布，且中间大于两边。考虑到激振力是施加于设备质心的，而设备有实际形状，所产生的加速度级大小不均是由设备的尺寸效应所致，与实际情况相符。将表1数据作为单基座模型、无偏心质量点模型以及偏心质量点模型的输入加速度载荷，分别得到6个评价点的振动加速度，并转化为加速度级，与原始模型中所得到的结果一同绘制于图7。

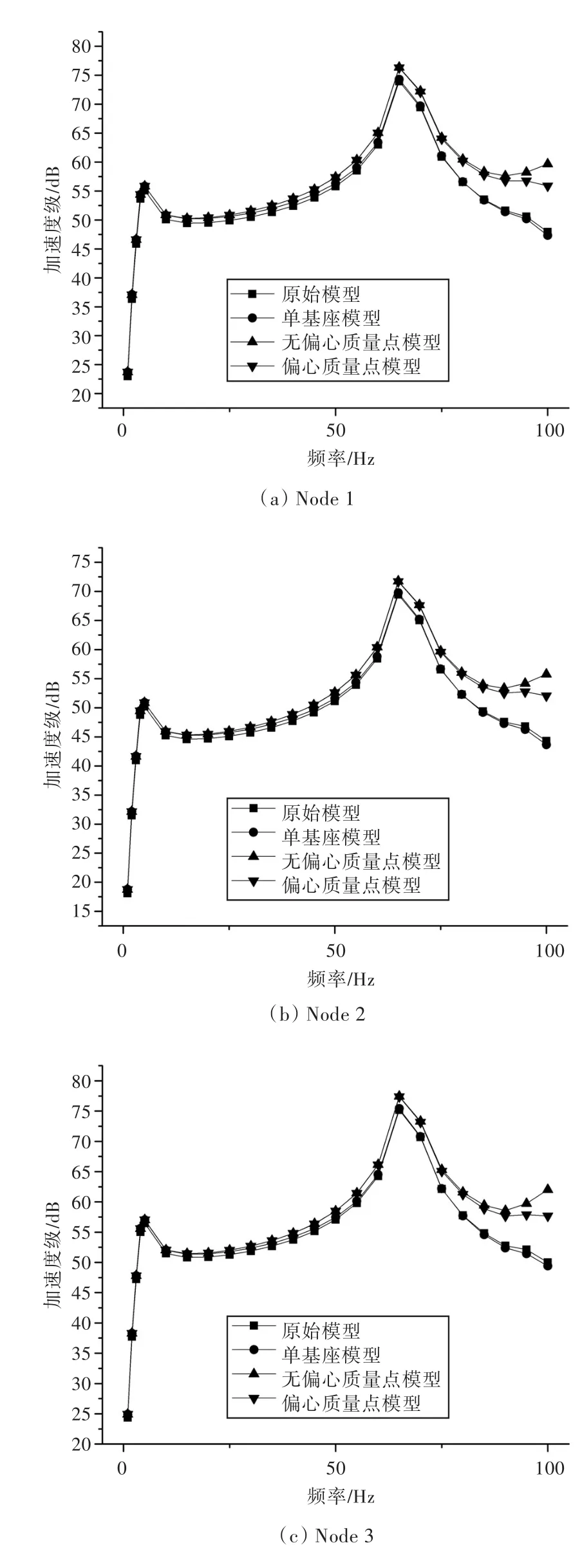
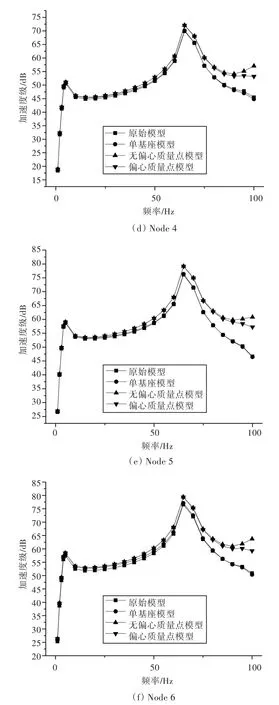
图7　直接法计算在6个评价点的加速度级Fig.7　Acceleration level of the 6 check points calculated by direct method

对比分析图7可知，原始模型与单基座模型在每一频率下的振动加速度级都接近一致。而无偏心质量点模型与偏心质量点模型在低频段与原始模型的结果比较接近，但在高频段与原始模型结果相差较大，其中，无偏心质量点模型相差更大，误差已超过50%。

图7的频率响应计算采用的是直接法，而在实际工程计算中，当面对复杂的船体模型时，直接法会出现无法求解的情况，此时，运用模态叠加法计算频率响应更普遍。对于本算例而言，设备质量29 t，模型总质量50 t，去掉设备后单基座模型质量21 t，单基座模型与原始模型模态相差较大，因此验证通过模态叠加法计算的结构动力响应结果更有实际意义。本文通过模态叠加法计算了4个模型的频率响应，分别得到6个评价点的振动加速度，并转化为加速度级，如图8所示。

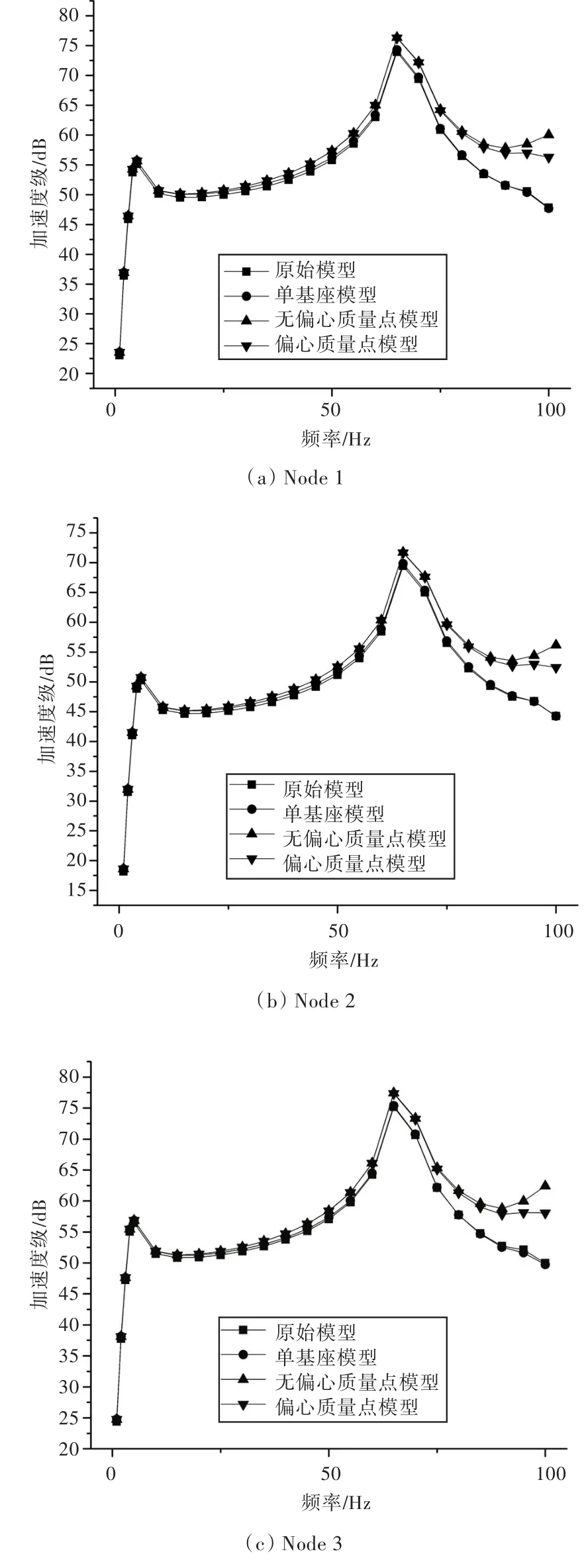
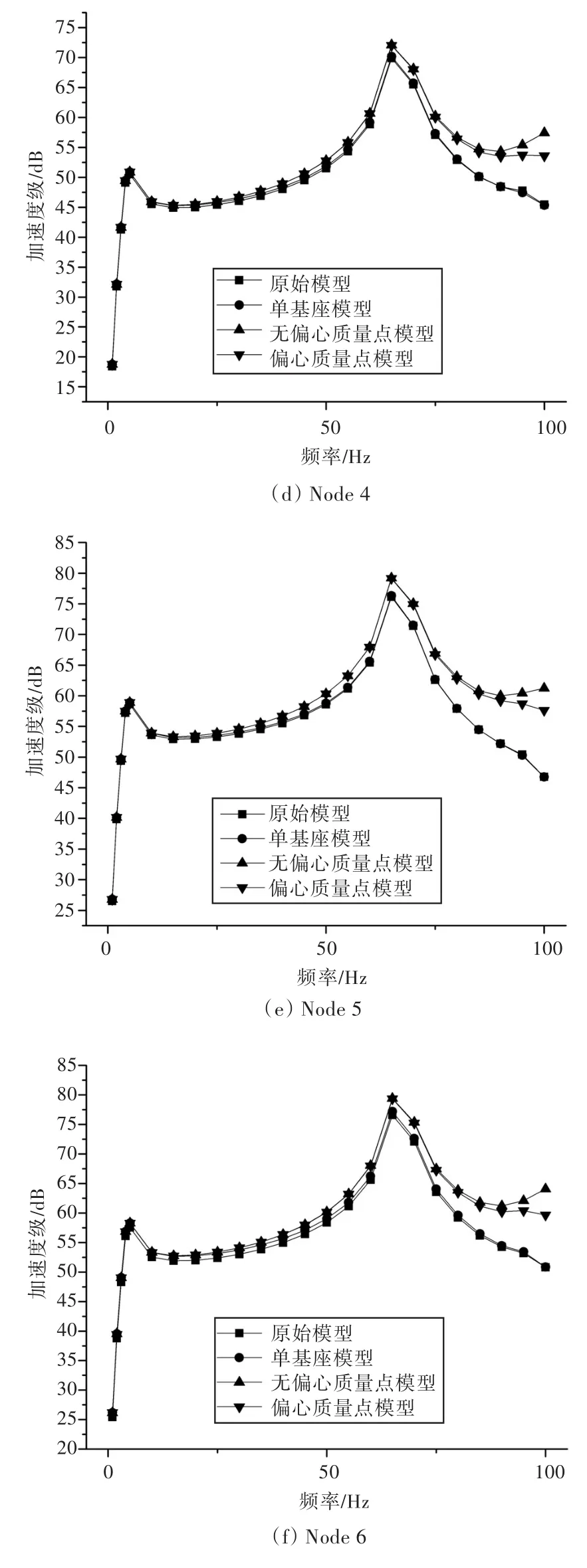
图8　模态叠加法计算在6个评价点的加速度级Fig.8　Acceleration level of the 6 check points calculated by mode superposition method

通过对比可知，模态叠加法计算结果与直接法结果一致，说明在原始模型，即“设备—基座”系统中施加激振力外载荷与在单基座模型，即“基座”系统中施加相应加速度外载荷所得的结果具有等效性，且对于直接法与模态叠加法均适用。说明在质点系统中论证的结果也可以推广到连续系统中。

2.3不同隔振器刚度下模型等效性验证

在有限元建模，尤其是在整船建模时，常需要调整模型的质量质心使之与实船相同，以检验模型对于实际的模拟程度，这也是目前工程计算中验收方验收模型时的重要评价指标［12］。虽然之前的推导和计算结果都表明，在原始模型，即设备—基座系统中施加激振力与在单基座模型，即基座系统中施加等效加速度外载荷所得的振动响应结果具有一致性，但若按照单基座模型施加加速度的加载方式，必然会导致模型整体质量缺失和质心偏移较大等结果，无法准确判断模型对于实际情况模拟的好坏。而观察图7与图8中的对比结果，发现在0～67 Hz之间，4种模型的结果都十分接近（通过模态计算得知67 Hz为基座的固有频率，在该频点处发生了共振，故而出现振动峰值）。如果在低频段内4种模型计算结果均具有等效性，为保证模型质量质心与实际情况一致，则在低频域内评价振动响应时，4种建模方式均可采用。因此，为验证在低频段内4种模型之间是否均具有等效性，将原模型的隔振器刚度分别增加2个量级、减小2个量级后重新计算，即分别令K=200 000 N/mm 和K=20 N/mm，计算4种模型在6个评价点的加速度，所得结果分别如图9与图10所示。

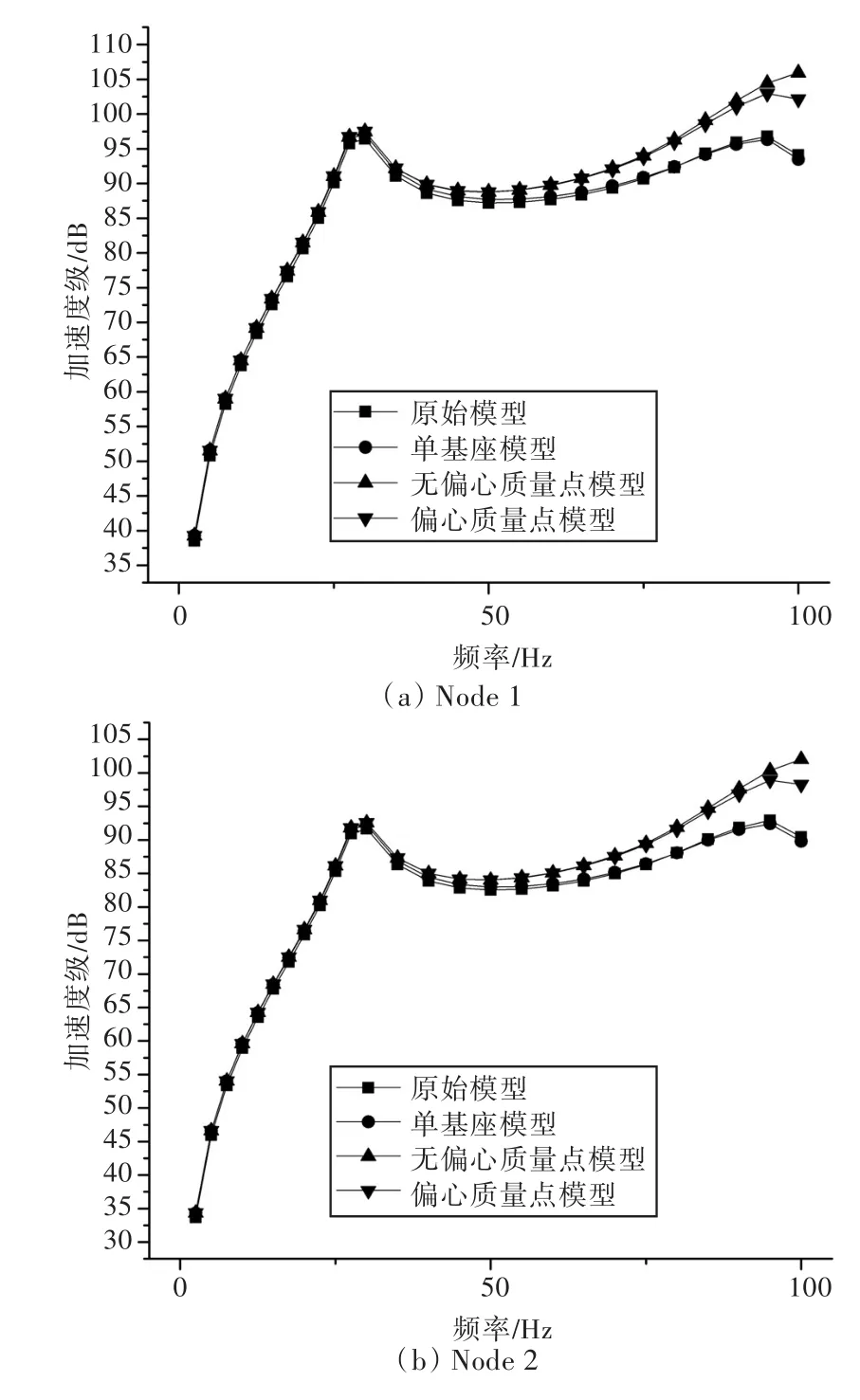
图9　隔振器刚度K=200 000 N/mm时6个评价点的加速度级Fig.9　Acceleration level of the 6 check points vibration isolator when K=200 000 N/mm

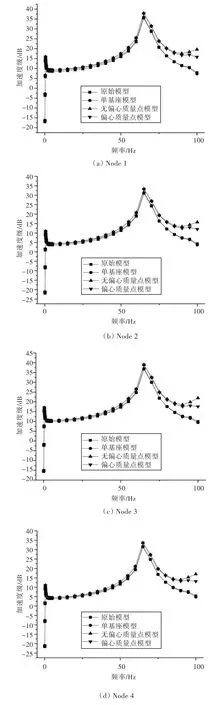
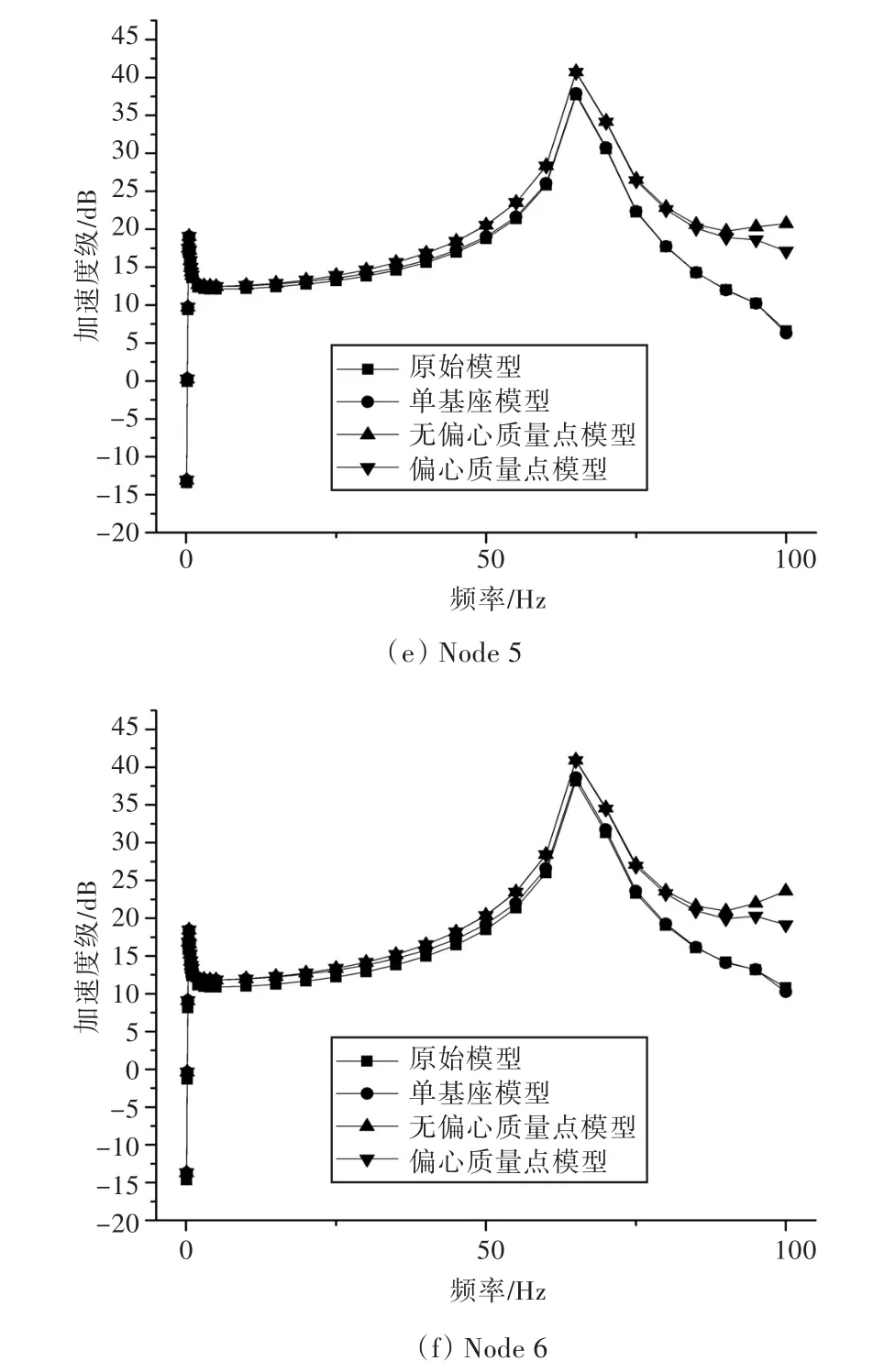
图10　隔振器刚度K=20 N/mm时6个评价点的加速度级Fig.10　Acceleration level of the 6 check points vibration isolator when K=20 N/mm

对比图9与图10中的曲线可以看出，在低频域段，4种建模方式的曲线重合度很高，说明在低频域段，施加加速度外载荷的3个模型对施加激振力外载荷的原始模型的模拟都具有相当的精度。但随着频率的增加，尤其是在基座的固有频率之后，无偏心质量点模型和偏心质量点模型与原始模型结果相差越来越大，已经不可用于实际工程的建模中。在实际工程计算中，所关心的频率不只是低频段的振动响应结果，而大多是从0～100 Hz，甚至是整个频域下的振动响应情况，此时若提供的外载荷是加速度外载荷，则采用单基座模型进行有限元建模将更为合理。

3　结　论

本文针对低频域，首先通过理论推导，分析了在“设备—基座”双自由度系统中施加激振力外载荷与在“基座”单自由度系统中施加相应的加速度外载荷时振动响应的等效性。之后，通过有限元模型分析将质点系的规律推广到了连续系统中。基于未给定设备和隔振器的动力学参数，只给定设备通过隔振器传递到基座面板处的加速度的工程实际情况，根据理论提出了一种单基座有限元模型和2种常用的质量点有限元模型。通过对振动加速度级计算结果的对比，得出与原始模型具有完全等效性的模型，验证了理论推导，并得到如下结论：

1）在船舶结构振动预报分析的有限元建模中，不同的外载荷输入方式对模型建立影响很大。在模型建立过程中，要根据给定的外载荷输入方式选择正确的建模方式，且要保证模型与实际结构中各部分属性相同，加载位置相同。

2）在船舶结构振动预报分析的有限元建模中，若给定外载荷为激振力，则建模时需要将设备、隔振器、基座完全建模，将激振力施加于设备的相应位置，此时整船质量不会缺失，可以通过分析模型质量和质心位置判断模型对实际情况模拟的优劣；若给定外载荷为加速度，则建模时只需考虑基座，不需对设备与隔振器建模，将加速度施加于基座面板相应位置，此时整船质量会缺少设备质量，在调整模型质量质心时，可以先将设备用质量点模拟，待调整完成后删去即可。

3）在原始模型，即“设备—基座”系统中施加激振力外载荷与在单基座模型，即“基座”系统中施加相应加速度外载荷所得的结果具有等效性。质量点模型在低频段与原始模型振动响应计算结果相近，而随着频率的增大，与原始模型偏离程度也增大。因此，可以在关心频率范围较低时选用质量点模型，保留设备质量。

［1］ 金咸定，夏利娟.船体振动学［M］.上海：上海交通大学出版社，2011.

［2］FULFORD R A，GIBBS B M.Structure-borne sound power and source characterization in multi-point-connected systems，part 2：about mobility functions and free velocities［J］.Journal of Sound and Vibration，1997，220（2）：203-224.

［3］ 刘见华，金咸定.结构声传递数值计算方法的研究进展［J］.振动与冲击，2002，21（4）：44-49.

LIU Jianhua，JIN Xianding.Research advances of numerical computing methods for structure-borne propagation［J］.Journal of Vibration and Shock，2002，21 （4）：44-49.

［4］庞福振.船舶结构噪声截断模型数值预报方法研究［D］.哈尔滨：哈尔滨工程大学，2012.

［5］FIEDLER C H，SCHNEIDER H G.BeTSSi-subbenchmark target strength simulation submarine［R］. Kiel：Forschungsanstalt der Bundeswehr für Wasserschall und Geophysik，2002.

［6］ 李俊，金咸定，刘见华.多自由度无阻尼动力吸振器的理论研究［J］.振动测试与诊断，2003，23（2）：99-101.

LI Jun，JIN Xianding，LIU Jianhua.Theoretical research on undamped vibration absorber with multidegrees of freedom［J］.Journal of Vibration，Measurement and Diagnosis，2003，23（2）：99-101.

［7］金咸定.船舶结构动力学的进展与信息化［J］.振动与冲击，2002，21（4）：1-6.

JIN Xianding.Advance in ship structure dynamics and application of information technology［J］.Journal of Vibration and Shock，2002，21（4）：1-6.

［8］邹春平，陈端石，华宏星.船舶结构振动特性研究［J］.船舶力学，2003，7（2）：102-115.

ZOU Chunping，CHEN Duanshi，HUA Hongxing. Study on structural vibration characteristics of ship［J］. Journal of Ship Mechanics，2003，7（2）：102-115.

［9］ 王宇，陈兴林，李光民.隔振器对舰船基座振动特性的影响［J］.舰船科学技术，2012，34（1）：30-35，49.

WANG Yu，CHEN Xinglin，LI Guangmin.Influence of vibration isolators to the vibration characteristics of a ship foundation［J］.Ship Science and Technology，2012，34（1）：30-35，49.

［10］ 田正东，计方.阻振质量刚性隔振在舰船基座结构中应用研究［J］.船舶力学，2011，15（8）：906-914.

TIAN Zhengdong，JI Fang.Applied research on rigid vibration isolation of blocking mass in hull base structure［J］.Journal of Ship Mechanics，2011，15（8）：906-914.

［11］ JANSSEN M H A，VERHEIJ J W，THOMPSON D J. The use of an equivalent forces method for the experimental quantification of structural sound transmission in ships［J］.Journal of Sound and Vibration，1999，226（2）：305-328.

［12］杨德庆，王德禹，刘洪林.舰艇振动声学特性数值分析［J］.上海交通大学学报，2002，36（11）：1537-1539，1543.

YANG Deqing，WANG Deyu，LIU Honglin.Numerical analysis of vibro-acoustic characters of ship［J］. Journal of Shanghai Jiaotong University，2002，36 （11）：1537-1539，1543.

The influence of dynamic loads on the FE model of the ship equipment-base system

YU Yang1，2，YANG Deqing1，2，LIU Jianhua3，SHI Jiaxin1，2

1 State Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China
2 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China
3 Marine Design and Research Institute of China，Shanghai 200011，China

In ship dynamic response analysis，it is through the equipment base that the dynamic load of ship equipment passes onto the deck，which is called“equipment-base system”.Generally，since it is usually difficult to measure the equipment exciting force yet much easier in measuring the acceleration passed onto the base panel，the research about relevant model-building and the ship dynamic response equivalence of applying these two kinds of loads is of high application value for real projects.Firstly，based on theoretical derivation，the influence of these two kinds of dynamic loads on modelling is analyzed in the particle vibration system.Then，two FE models of a specific hull of an actual ship is established to confirm the validity of the conclusion by comparing the acceleration level of the check points in these two FE models，where one of which is an equipment-base model loaded with exciting force and the other is a single base model loaded with acceleration.The result shows that in the low frequency domain，when the type of dynamic load on the“equipment-base system”is acceleration，it is unnecessary to incorporate equipment or consider its mass in the FE model.

dynamic load；equipment-base system；equivalence；acceleration

U661.44

A

10.3969/j.issn.1673-3185.2016.04.014

2015-12-07网络出版时间：2016-7-29 9:45

国家自然科学基金资助项目（11072149）

郁扬，男，1990年生，硕士生。研究方向：船舶与海洋工程结构振动及噪声控制。

E-mail：astrologer@sjtu.edu.cn

杨德庆（通信作者），男，1968年生，博士，教授。研究方向：船舶与海洋工程结构振动及噪声控制，船舶结构优化设计。E-mail：yangdq@sjtu.edu.cn