基于有限元能量流的混合结构间耦合损耗因子

陈景昊，吴卫国，林永水

1中国船级社温州办事处，浙江温州3250002武汉理工大学交通学院，湖北武汉430063

基于有限元能量流的混合结构间耦合损耗因子

陈景昊1，2，吴卫国2，林永水2

1中国船级社温州办事处，浙江温州325000
2武汉理工大学交通学院，湖北武汉430063

为了减轻船舶结构重量，降低重心，高速船往往采用钢、铝混合结构，两者之间采用过渡接头进行连接会影响结构声波的传递。耦合损耗因子（CLF）作为统计能量分析法的一个关键参数，对船舶舱室噪声预报有着重要影响。基于有限元能量流法构建了相应的数值计算模型，采用Matlab软件编写计算程序，将其应用于某典型钢、铝混合结构的计算中并对其进行了验证，同时还研究了连接接头参数及加筋板对结构耦合损耗因子的影响，结果表明：增加接头的重量或横截面积可以减小中高频段的耦合损耗因子。所编程序可以为该类型船舶的噪声预报及减振降噪提供建议与指导。

耦合损耗因子；有限元能量流法；统计能量分析法；钢、铝混合接头

0　引　言

高速船在设计建造时，为了达到减轻重量、降低重心、提高航速等目的，往往采用钢、铝混合结构，即主船体采用钢质结构，上层建筑采用铝合金结构，铝合金上层建筑与钢质结构之间用过渡接头连接［1］（图1）。过渡接头的存在影响了结构声波的传递，进而影响结构间耦合损耗因子（CLF）。对于大多数高速船舶，其大部分客舱均位于主甲板以上，钢质主船体与铝合金上层建筑之间的特殊连接结构会影响结构声波的传递，进而影响该处的耦合损耗因子，对上层建筑客舱舱室噪声预报的精度有很大影响。在诸多复杂的实际工程中，受困于无法准确求取统计能量参数，使统计能量分析法的发展受到了很大的限制。

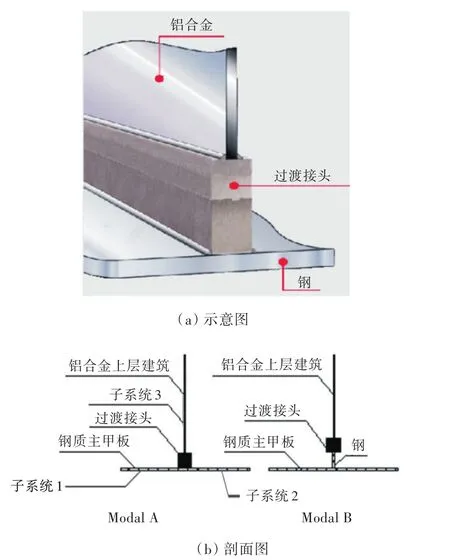
图1　常用钢、铝过渡接头及其连接形式Fig.1　Common types of steel-aluminum transition junction and connection forms

结构间耦合损耗因子作为子系统间耦合作用大小的表征，一直是研究的难点和热点［2-3］。Simmons［4］提出了采用有限元方法预测结构耦合损耗因子；Mace等［5］对该方法进行了更为深入的研究，其建立的计算模型适用于强耦合复杂结构间耦合损耗因子的计算；卢兆刚［6］和张瑾［7］等利用该方法对某些典型结构的中频阶段的能量流动及耦合损耗因子进行了相应的分析。吴雄祥［8］和林永水［9］等分别采用阻抗法和输入功率法对钢、铝混合结构耦合损耗因子进行了相应的研究。本文将基于有限元能量流法建立相应的数值计算模型并利用Matlab软件编写计算程序，对钢、铝混合结构的耦合损耗因子进行计算，并验证其可靠性，同时还研究过渡接头各参数对结构耦合损耗因子的影响。

1　理论分析

1.1能量平衡方程

根据子系统间功率流模型，具有N个子系统的复杂结构子系统间能量平衡方程表达式如下

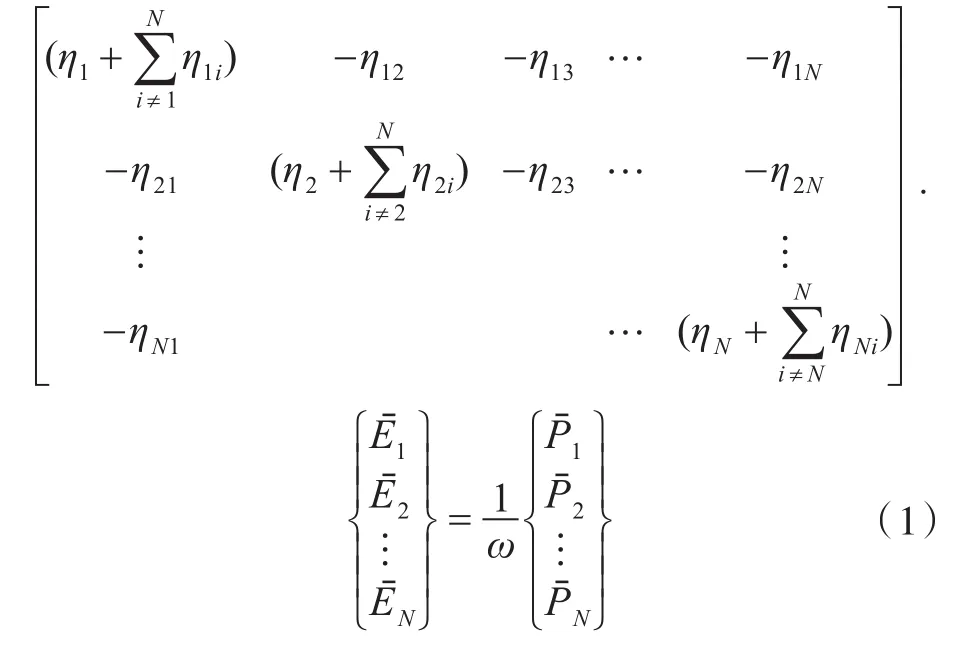
式中：ηi为阻尼损耗因子；ηij为耦合损耗因子；Eˉi为系统i的平均能量；ω为中心角频率；Pˉi为系统i的平均输入功率。

为了便于理解，将本文要讨论的T型结构划分为3个子系统，即模型中2块钢质主甲板设为子系统1和子系统2，过渡接头以及铝质上层建筑设为子系统3，如图1（b）所示。由式（1）可知具有3个子系统的耦合结构的能量平衡方程为：

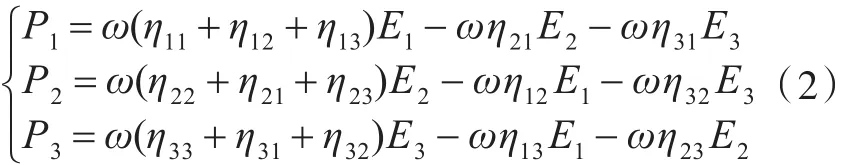
对每个子系统的输入功率以及振动能量进行空间平均和频域内平均后，方程可以写为：

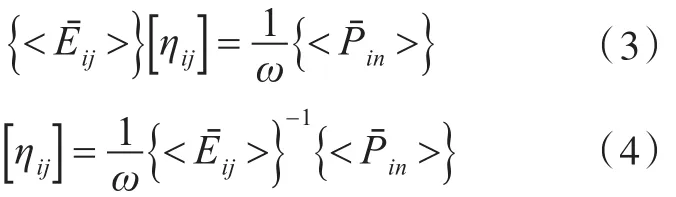
式中：

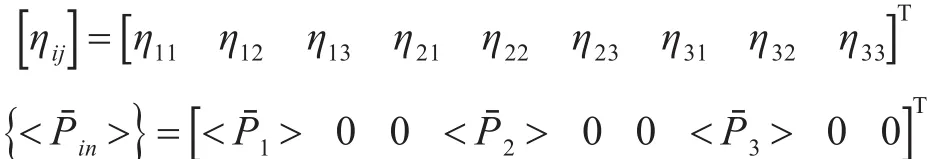
通过对3个子系统逐次进行激励，结合式（4）列出9个方程即可得到损耗因子矩阵。

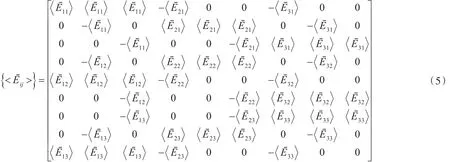
1.2输入功率

在数值计算中，由于激励点作用在节点上，作用面积可以忽略，因此可以将输入功率的作用视为点源的输入，即将激励作用在某个节点上，假定激励力f（t）为单频激励，值为

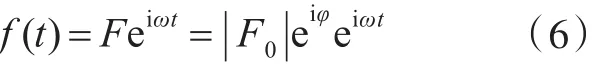
式中：F为激励力的复数形式；F0为激励力的最大幅值；ω为圆频率；φ为相位角。

速度v（t）为

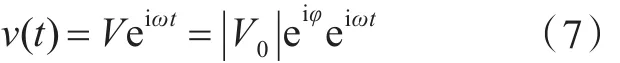
式中：V为速度的复数形式；||V0为激励力的最大幅值。

在一个周期内的时间平均输入功率为

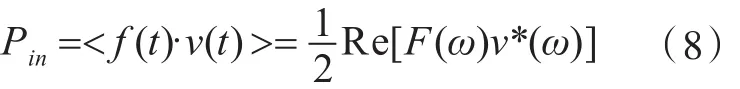
式中：＜·＞为时间上的平均值；F（ω）为激励力；v*（ω）为响应速度幅值V（通常为复数）的共轭复数；Re为取实部。

当激励作用于子系统时，其在频域与空间上的平均输入功率为

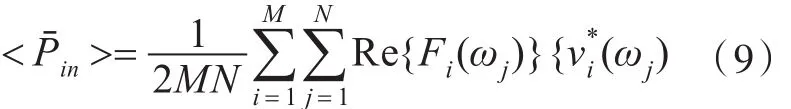
式中：M为作用在子系统上激励点的个数；N为中心频率带宽内的计算频率点个数。

1.3子系统振动能量

1.3.1子系统中的低频振动能量

一般系统的动力学方程可写作

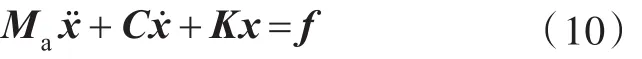
式中：向量x为系统的节点位移坐标；向量ẋ为系统节点的速度；ẍ为系统节点的加速度；f为系统所受的外力向量；Ma为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵。

由此可以求得系统的势能V，动能T分别为

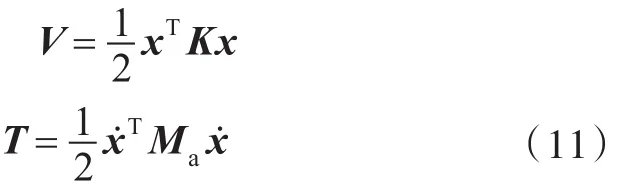
1.3.2子系统中的高频振动能量

在高频阶段，对于平板结构，当其处于共振模态时，其动能与势能近似相等，即振动能量等于动能的2倍，因此在高频阶段为了节约计算成本，子系统的振动能量E可由下式求得

式中：m为单位质量；＜v2＞为单位质量所对应的速度平方。

对模型进行有限元处理后，并对其振动能量进行空间平均和带内平均，子系统的振动能量可由下式求得

式中：m为子系统的质量；P为子系统总节点数。

2　数值仿真及验证

2.1模型参数

本文将结构模型简化为1个T型结构（图2），为了后文对仿真方法进行验证，本节将模型参数取为与文献［9］相同，如表1所示。

表1　模型具体参数Tab.1　The parameters of model

2.2数值仿真方法计算流程图

图3为本文模拟采用的数值仿真方法计算流程图。

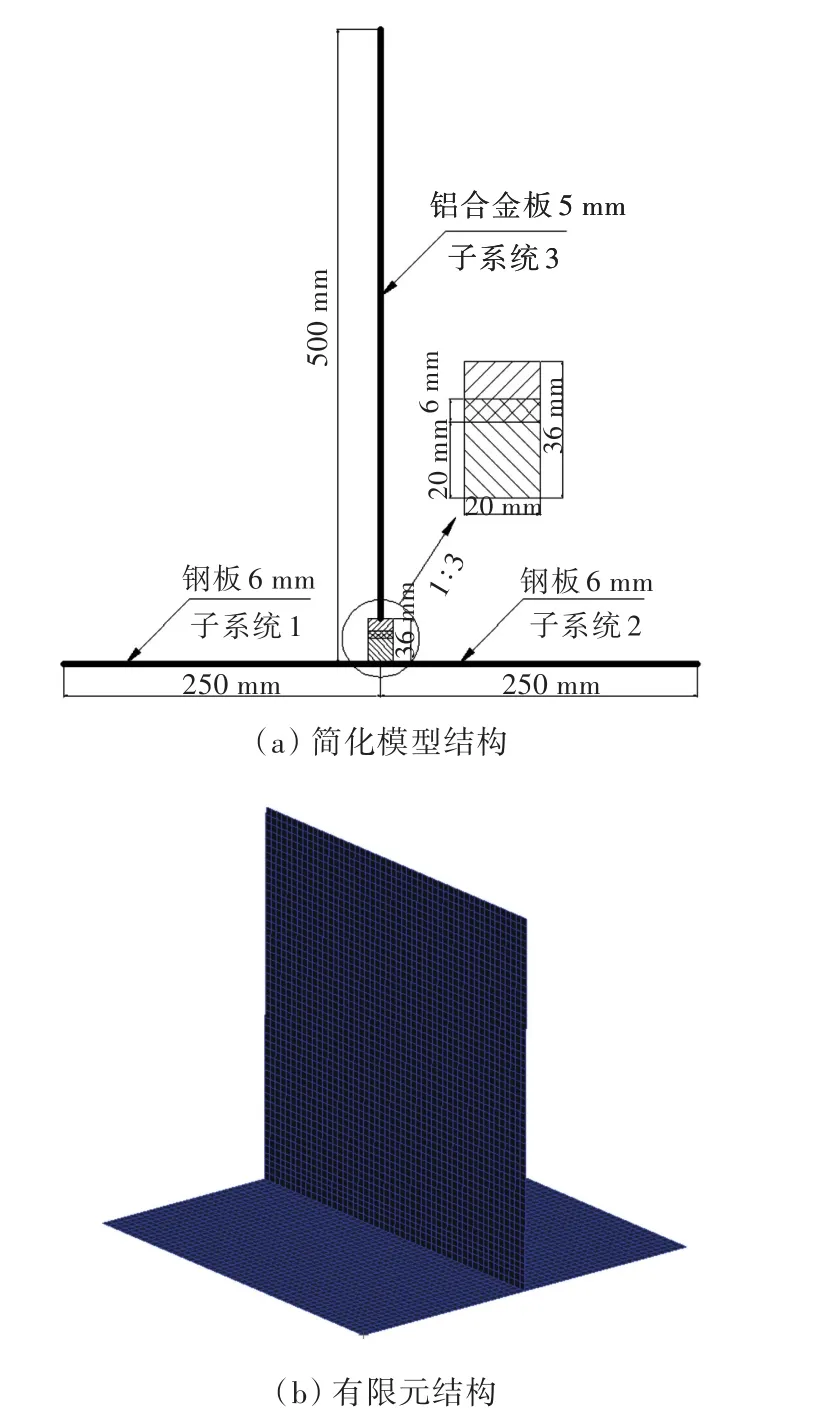
图2　简化模型结构及有限元结构图Fig.2　Simplified structure model and FEM model

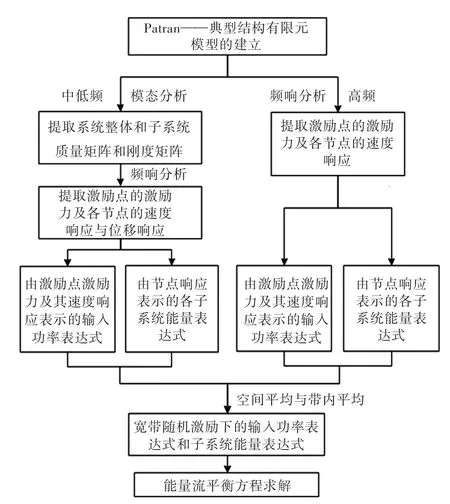
图3　耦合损耗因子数值计算流程图Fig.3　The calculation procedure of CLF

2.3计算参数的影响

2.3.1网格尺寸

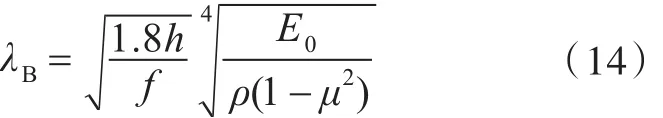
网格尺寸直接影响计算的效率和精度，在声学有限元分析中，一般应保证1个波长内至少有6个单元［10］，平板弯曲波波长可以写为

式中：E0为弹性模量；μ为泊松比；h为板厚；ρ为材料密度；f为频率。

根据本文所采用的模型以及要求的计算频率（400～8 000 Hz），利用式（14）对计算网格进行大致的估算，系统1和系统2所要求的网格尺寸不大于13.5 mm，系统3所要求的网格尺寸不大于12.3 mm。基于有限元能量流法和基于功率输入法，本节对不同网格尺寸模型进行了计算和对比分析（图4）。图中CLF13代表子系统1到子系统3的耦合损耗因子。对于网格尺寸为50 mm的模型，当中心频率超过3 150 Hz后有一些负值出现，与耦合损耗因子的特性不符，故在图中没有列出；对于网格尺寸为25 mm的模型，可以明显看出各耦合损耗因子曲线与其他几条曲线无论是在趋势上还是在数值上均有较大的差距；对于网格尺寸为15，12，10和8 mm（除个别频率外）的模型，趋势大致相同，数值也吻合得较好。因此可以认为对于该模型，当网格尺寸小于12 mm时计算精度可以保证。

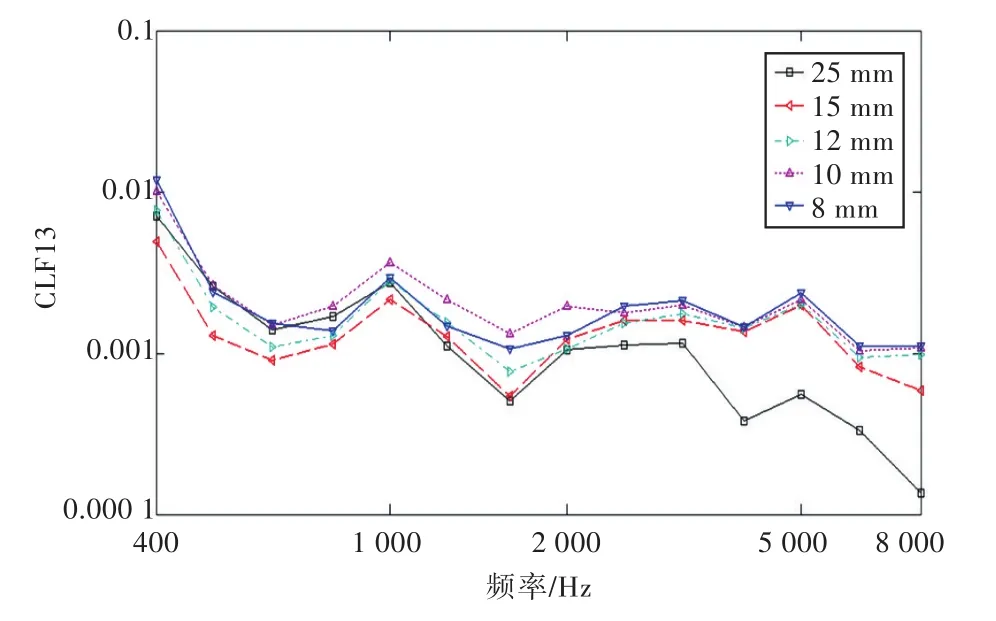
图4　网格尺寸的影响Fig.4　The influence of element size

2.3.2随机激励点的选取

为了使整体计算满足随机性的要求，激励点的选取必须随机确定，同时为了避免模型边界的影响，激励点的位置距边界的距离必须大于相应频率1/4弯曲波的波长［11］。由于点源激励输入会使得各个子系统间结构模态响应存在相关性，因此为了保证子系统各阶模态互不相关，需要采用多个不同激励点进行激励。但过多的激励点又会影响计算效率，本文对采用3个（P3模型）、6个（P6模型）和9个随机激励点（P9模型）的模型各取3组，将其计算结果进行了对比（图5）。经计算分析，对于采用3个独立激励点的3组P3模型，计算所得的耦合损耗因子曲线与采用6个独立激励点的P6模型以及9个独立激励点的P9模型所得的结果，在不少频率处有一定的差异，同时计算结果稳定性不佳；而对于P6模型和P9模型所得的6组结果在趋势上大致相同，在数值上误差基本在10%以内，因此可以认为采用6个独立激励点进行平均时，本文计算程序的精度可以保证。

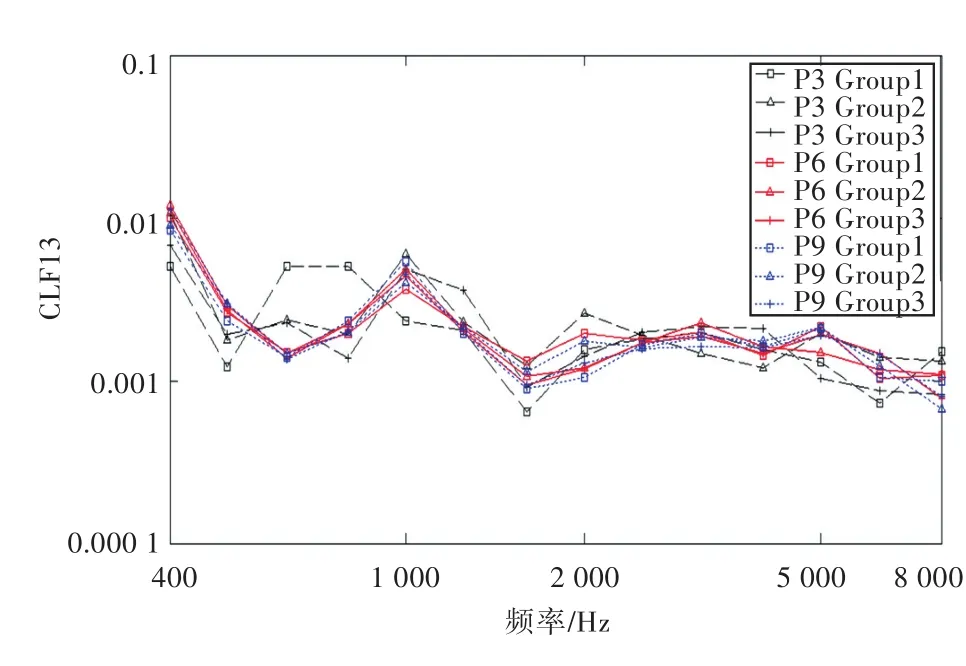
图5　激励点的影响Fig.5　The influence of excitation points

2.3.3模态频率响应分析中的模态截断

在模态频率响应分析中，并不需要涵盖全部模态，偏离分析频率较远的模态对计算结果的影响较小，将其考虑进来只会大量增加计算量，降低求解效率。对计算影响最大的是分析频率带宽内的共振模态，但是分析带宽的2～3倍范围内的模态对计算结果仍有一定的影响［12］，因此，为了保证精度，本文在计算时模态截断取为最高分析频率的3倍。

图6　钢、铝混合模型数值计算值与实验值对比Fig.6　Comparison of CLF for the mixed model obtained by simulation and experiment

1）未考虑模态阻尼随频率的变化，只给出了模态阻尼在中心频率下的平均值。

2）有限板边界上的节点能量响应值受边界效应的影响，对仿真结果有一定的影响。

3）对过渡接头的材料特性进行了简化，视为简单的钢和铝的组合，同时在子系统3能量求取时未计及接头的质量。

4）采用平均频率步长，可能无法准确提取分析频段内的某些响应峰值。

2.4.2铝质L型板模型的验证

由于文献［9］的实验结果频率上限为4 000 Hz，无法对高频阶段的仿真方法进行验证，本节采用对铝质L型板模型进行计算，通过与VA One软件计算的CLF曲线进行对比，验证其可靠性。模型为2块800 mm×800 mm×4 mm的铝板进行L型连接，有限元模型和VA One模型如图7所示。

2.4数值仿真方法的验证

2.4.1钢、铝混合结构模型的验证

利用本文的程序对文献［9］的实验模型进行计算，其耦合损耗因子（400～8 000 Hz）结果如图6所示。数值仿真计算时采取如下参数：子系统网格尺寸为10 mm，各子系统独立激励点为6个，模态截断取计算频率的上限3倍。

由于文献［9］中仅给出了400～4 000 Hz的实验结果，图6给出了该频段钢、铝混合模型耦合损耗实验值与数值仿真值的对比曲线。从图6可以看出，利用功率输入法和采用数值仿真方法计算所得的耦合损耗因子曲线，在趋势上保持了较好的一致性，除个别频率外，精度都在工程许可的范围内。根据对比结果，认为引起误差的主要原因有以下几点：

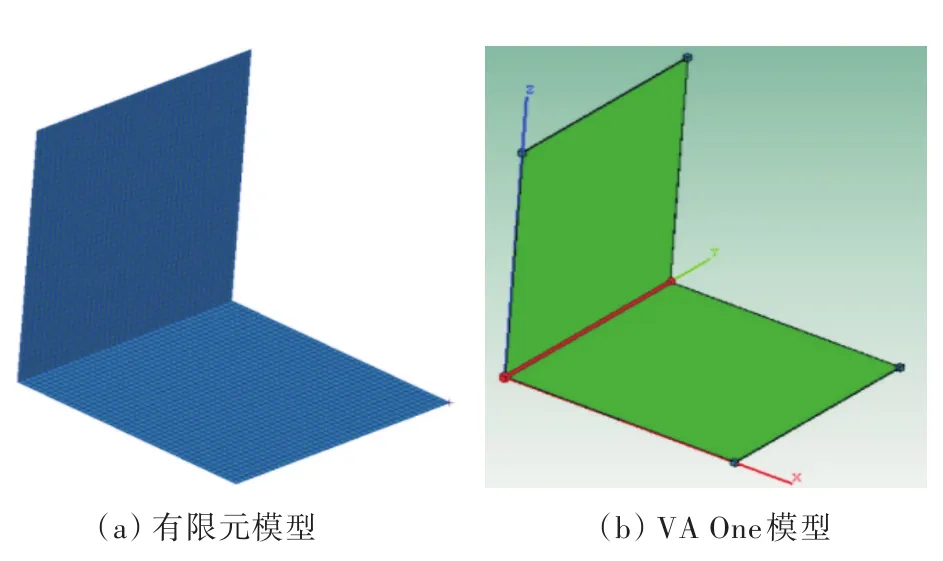
图7　铝质L型板有限元模型和VA One模型Fig.7　The FEM and VA One model of L-shaped plate

经计算，铝质L型板模型在100～8 000 Hz模态数均大于1，当中心频率大于500 Hz时，模型满足模态数大于5的要求；对于网格尺寸，模型在8 000 Hz时，对网格尺寸的要求为不大于11 mm。因此对该模型，计算时取子系统网格尺寸为10 mm，各子系统独立激励点为9个，模态截断取计算频率上限的3倍。

从图8可以看出，对于铝质L型板模型，利用本文计算方法和VA One（波分析法）软件计算得到的耦合损耗因子曲线，无论在趋势上还是在数值上均吻合得非常好，由此可见，本文的计算方法对中频和高频阶段一般模型的耦合损耗因子计算是可靠的。

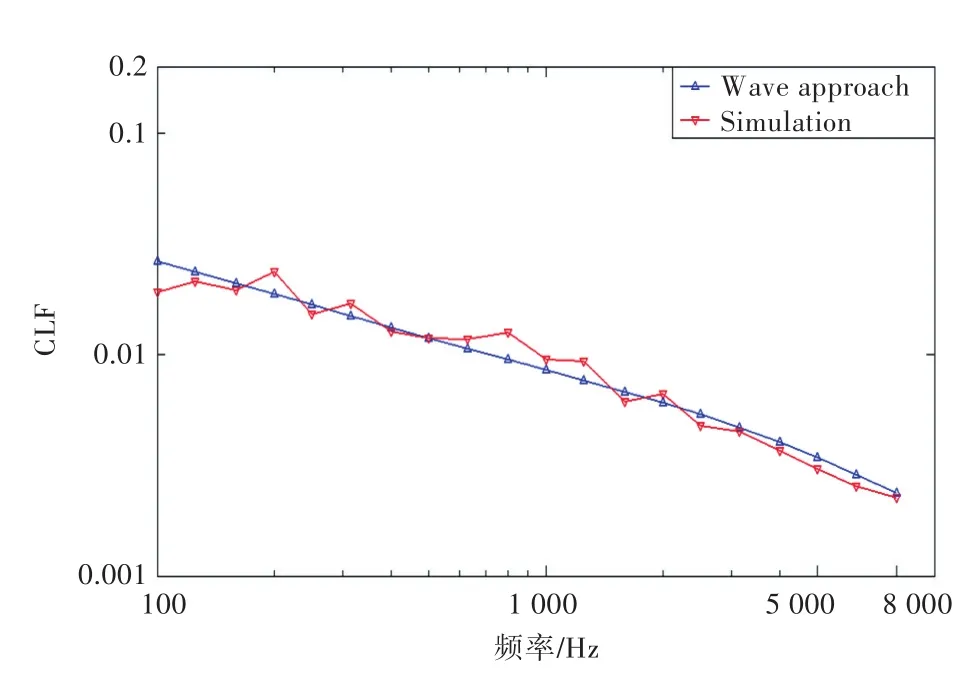
图8　铝质L型模型CLF波分析法与本文方法对比Fig.8　Comparison of L model's CLFs obtained by wave approach and simulation

3　接头参数及位置的影响

钢、铝混合结构连接接头的重量、截面形状、连接位置等均对该结构的能量传递有一定的影响。本节将运用本文的数值仿真方法，对接头的各参数及位置进行研究分析，为钢、铝混合结构船舶的振动噪声预报和控制提供指导。

图9（a）～图9（c）给出了是否含过渡接头以及不同接头位置（A模型为在连接处设接头，B模型为升高100 mm设接头，如图1（b）所示）情况下结构的CLF。总体来说，无接头模型和B模型的仿真值趋势较为相似，而A模型的接头在两板连接处，对能量的传递影响较大，后文将对接头质量和接头截面的影响做进一步探讨。

通过改变接头厚度来控制A模型接头的质量，对不同接头厚度以及无接头模型的耦合损耗因子进行了对比。从图9（d）～图9（f）中可以看出，无接头模型的CLF12是最大的，随着接头厚度的增加CLF12逐渐降低，主要原因是过渡接头起着阻抑作用，随着厚度的增加而增强。但对CLF13 和CLF31，无接头模型的值不是最大，主要原因是在中、低频段，过渡接头可能会增大结构的能量传递，且在一定厚度范围内，随接头增大作用增强，随着厚度的继续增加，过渡接头的阻抑作用才会表现出来。

在保证A模型接头质量不变的情况下，改变接头的截面参数，探究接头质量沿垂向布置和沿水平布置对耦合损耗因子的影响。从图9（g）～图9（i）中可以看出，随着接头高度的增加，采用各个接头高度情况下的耦合损耗因子曲线随频率的变化趋势较为一致，随着接头高度的增加，在低频阶段变化不是很明显，但在中、高频阶段，节点处的各个耦合损耗因子则逐渐降低，原因是在保持接头质量不变的情况下，增加接头截面的高度，以及降低接头截面的厚度能够增大过渡接头的转动惯量，在中、高频段有较好的阻抑效果，因此，在一定程度上可以降低耦合损耗因子。

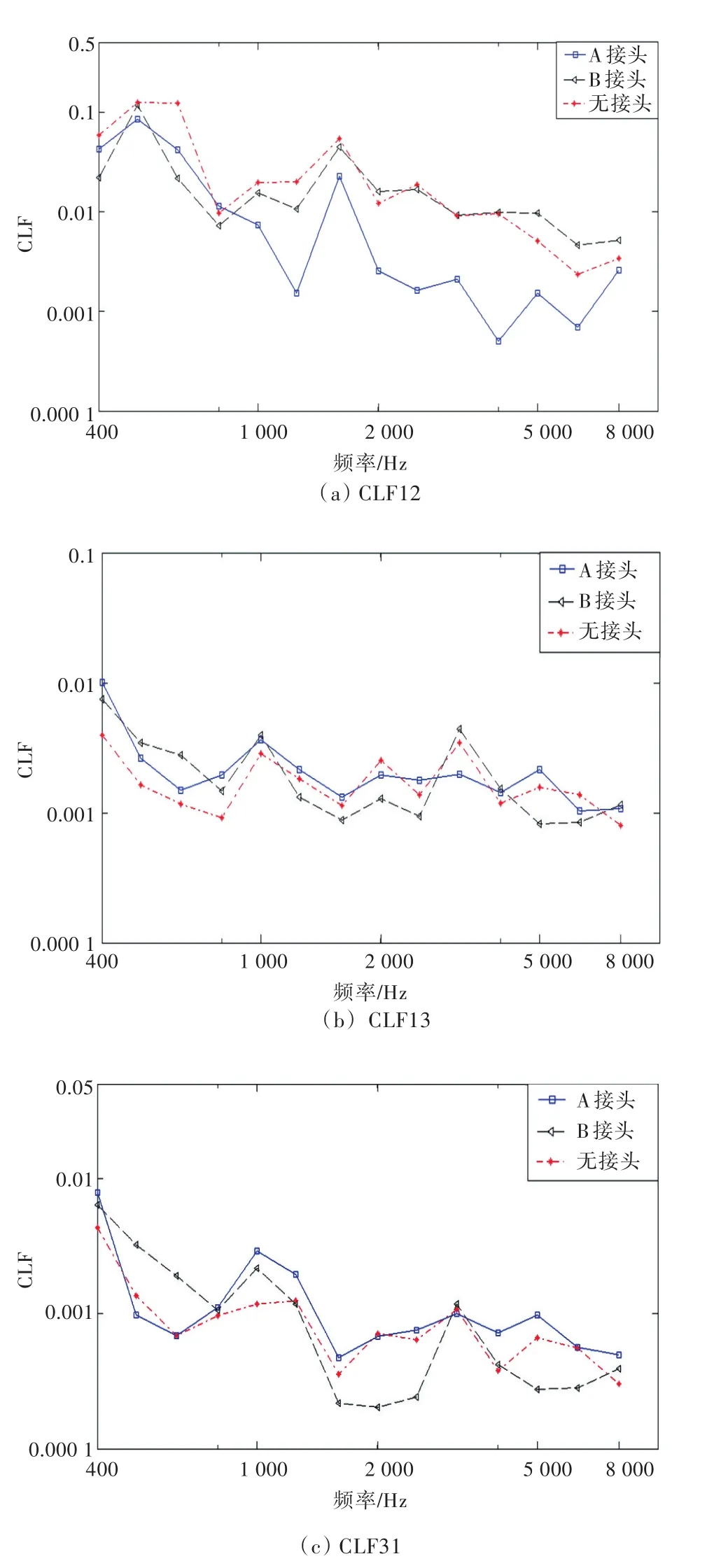
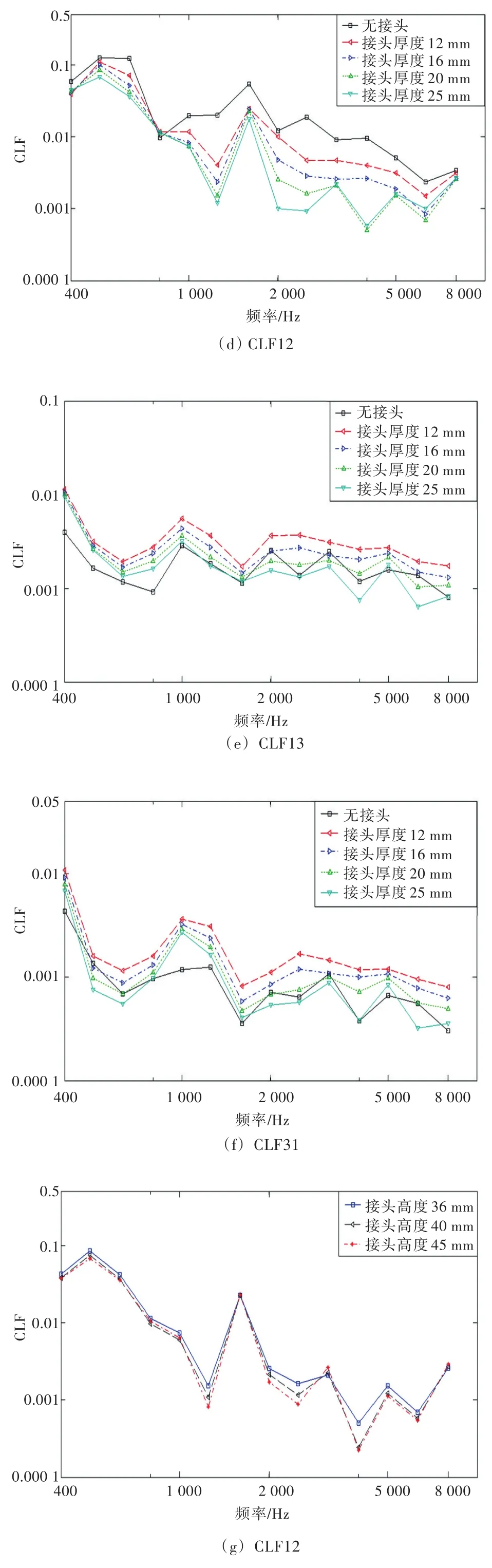
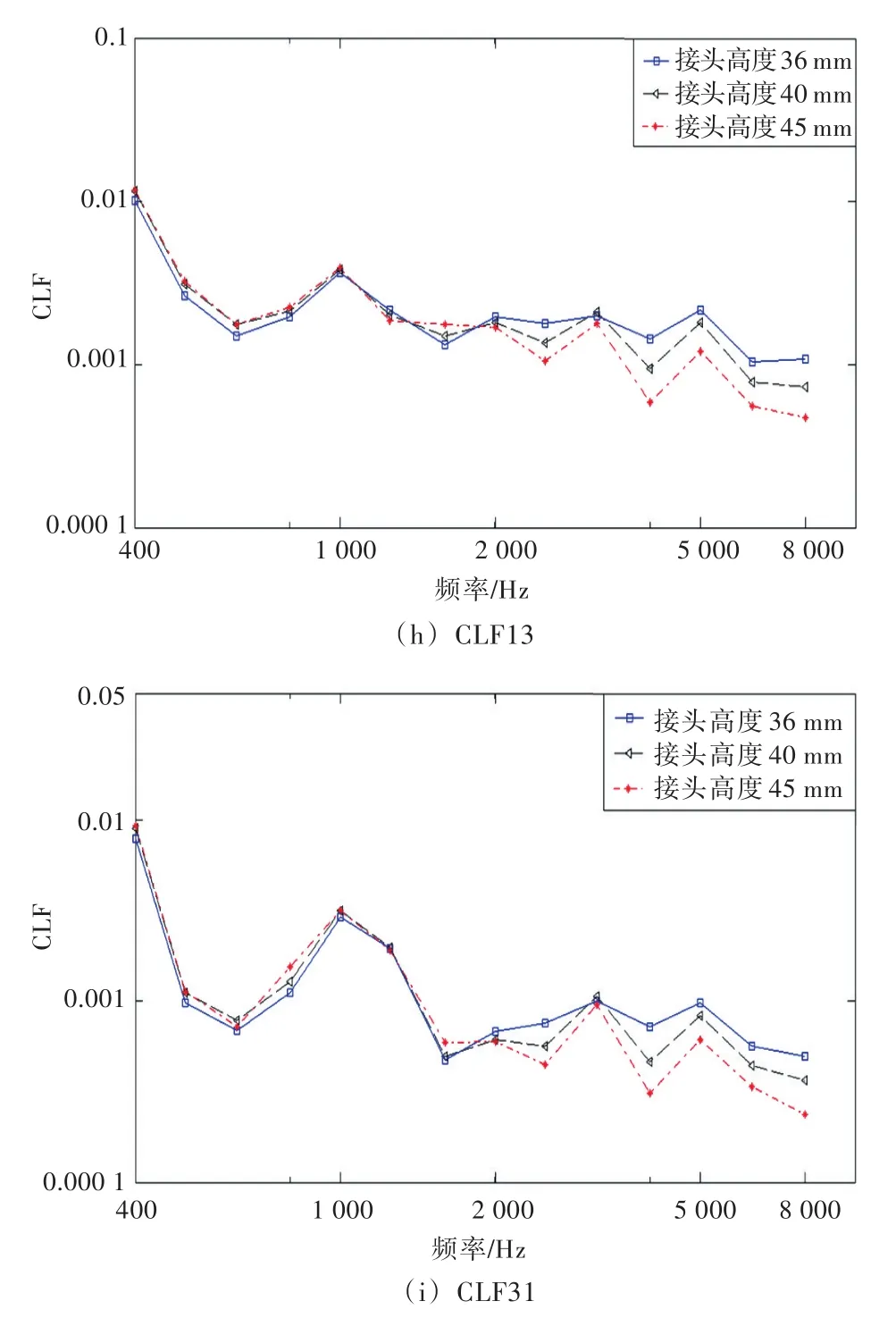
图9　接头参数及位置对CLF的影响Fig.9　The influence of junction parameter and position

船体结构多数是由加筋板结构组成，目前诸多学者采用统计能量分析法预报船舶噪声时，对加筋板结构采用了简化处理，而加筋板结构的模态特性与平板结构的模态特性有很大的差别，因此采用简化处理虽然提升了整体的计算效率，但是也影响了预报的精度，同时无法对某些特殊频率的振动特性做出准确的预测。通过在原模型的3个子系统中点处加设20 mm×4 mm的加强筋，建立相应的有限元模型并进行计算，其与原模型的耦合损耗因子对比曲线如图10所示，由于板子系统加筋后固有频率上升使得加筋板模型的耦合损耗因子曲线变化更为平缓，同时曲线整体略有向高频移动的趋势。

4　结　论

本文对混合结构间耦合损耗因子进行了研究，提出的计算方法和研究结论对提高混合结构船舶的噪声预报精度及减振降噪具有重要意义，主要研究结论如下：

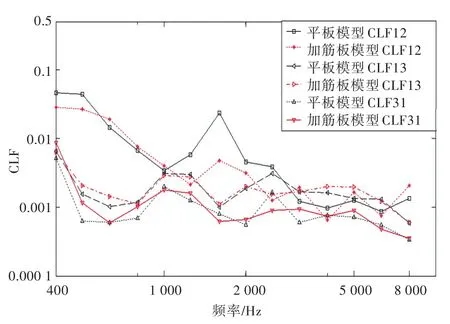
图10　平板模型与加筋板模型耦合损耗因子对比Fig.10　Comparison of plate model and stiffened plate model

1）基于有限元能量流法建立相应的数值计算模型并编写了相关的计算程序，通过与文献［9］的模型实验以及L型铝质板的波分析法计算结果进行对比，验证了该方法对中、高频钢、铝混合结构耦合损耗因子计算的可靠性。

2）对计算程序的主要参数进行了研究，为数值仿真计算中主要参数的选取提供了建议。

3）结合本文提出的计算方法对连接接头的布置和参数的影响进行研究，结果表明：增加接头的重量或横截面积可以减小中、高频段的耦合损耗因子。

［1］王承权，张京立.舰船钢—铝结构过渡接头的应用及节点设计［J］.船舶工程，2004，26（6）：34-38.

WANG Chengquan，ZHANG Jingli.Application and nodal point design of Structural Transition Joint（STJ）in ship with steel-aluminum superstructure［J］.Ship Engineering，2004，26（6）：34-38.

［2］ 姚德源，杨福家，王其政.统计能量分析原理及其应用［M］.北京：北京理工大学出版社，1995.

［3］LYON R H，DEJONG R G.Theory and application of statisticalenergyanalysis［M］.London： Butterworth-Heinemann，1995.

［4］SIMMONSC.Structure-bornesoundtransmission through plate junctions and estimates of SEA coupling loss factors using the finite element method［J］.Journal of Sound and Vibration，1991，144（2）：215-227.

［5］MACE B R，SHORTER P J.Energy flow models from finite element analysis［J］.Journal of Sound and Vibration，2000，233（3）：369-389.

［6］ 卢兆刚，郝志勇，郑旭.基于有限元能量流模型的复杂耦合结构中低频段耦合损耗因子的计算［J］.振动与冲击，2011，30（11）：42-46.

LU Zhaogang，HAO Zhiyong，ZHENG Xu.Coupling loss factor calculation of complex coupling structure based on finite element energy flow model［J］.Journal of Vibration and Shock，2011，30（11）：42-46.

［7］张瑾，马兴瑞，韩增尧，等.基于有限元的能量流分析方法研究［J］.振动与冲击，2012，31（8）：47-51.

ZHANG Jin，MA Xingrui，HAN Zengrao，et al.Energy flow analysis based on finite element method［J］. Journal of Vibration and Shock，2012，31（8）：47-51.

［8］吴雄祥.高速船典型节点耦合损耗因子研究［D］.武汉：武汉理工大学，2013.

［9］林永水，吴卫国，陈景昊，等.钢铝结构连接耦合损耗因子计算方法研究［J］.振动与冲击，2015，34 （3）：204-209.

LIN Yongshui，WU Weiguo，CHEN Jinghao，et al.A new calculating method for coupling loss factor of a steel-aluminum junction［J］.Journal of Vibration and Shock，2015，34（3）：204-209.

［10］李增刚，詹福良.Virtual Lab Acoustics声学仿真计算高级应用实例［M］.北京：国防工业出版社，2010.

［11］LIN T R，TAN A C C，YAN C，et al.Vibration of L-shaped plates under a deterministic force or moment excitation：a case of statistical energy analysis application［J］.Journal of Sound and Vibration，2011，330（20）：4780-4797.

［12］田利思，李相辉，马越峰，等.MSC Nastran动力分析指南［M］.北京：中国水利水电出版社，2012.

The coupling loss factor of mixed structures based on the finite element energy flow model

CHEN Jinghao1，2，WU Weiguo2，LIN Yongshui2

1 Wenzhou Office，China Classification Society，Wenzhou 325000，China
2 School of Transportation，Wuhan University of Technology，Wuhan 430063，China

The aluminum-steel structure is often applied to high speed vessels for the purpose of weight reduction，declining center of gravity，and high speed.The transition joint between the steel-made main hull and aluminum alloy superstructure could affect the propagation of structure acoustic waves，thus affecting the Coupling Loss Factor（CLF）between these structures，a key parameter of Statistical Energy Analysis （SEA）and significantly impacts the prediction of noise.Based on the finite element energy flow method，a numerical computation model and corresponding calculation program in Matlab are developed，which are then verified with experiment and L model's wave approach results.The influence of calculation parameters on accuracy is studied and relevant suggestions are given.Particularly，the effect of joint parameters on CLF is studied，suggesting that the thickness ratio of plate and joint has a large impact to the CLF；the energy flow features of the stiffened plate model is studied，indicating that compared with the flat model，the CLF curve of the stiffened plate model is more mild.Overall，the proposed program and the findings in this paper provide guidance for noise prediction and reduction in marine engineering.

Coupling Loss Factor（CLF）；finite element energy flow method；Statistical Energy Analysis （SEA）；steel-aluminum transition junction

U661.44

A

10.3969/j.issn.1673-3185.2016.04.012

2015-09-24网络出版时间：2016-7-29 9:45

工业和信息化部高技术船舶专项资助项目（工信部联装［2010］337号）；中央高校基本科研业务费专项资金资助项目（2014-zyo-22）

陈景昊，男，1990年生，硕士。研究方向：结构振动与噪声控制。

E-mail：chenjinghao@ccs.org.cn

吴卫国（通信作者），男，1960年生，硕士，教授。研究方向：船舶振动与噪声控制，结构安全性与可靠性，结构动力与稳定性研究。E-mail：mailjt@163.com