基于体积力法的全附体KCS型船模PMM运动数值模拟

王慧婷，毕毅

海军工程大学舰船工程系，湖北武汉430033

基于体积力法的全附体KCS型船模PMM运动数值模拟

王慧婷，毕毅

海军工程大学舰船工程系，湖北武汉430033

为高效、精确地求解船舶操纵水动力导数，以全附体KCS型船模为研究对象，基于RANS方程及VOF模型，在star-ccm+平台上采用体积力法模拟螺旋桨作用，计及自由面兴波及航行姿态变化对船模水动力的影响，开展斜航、纯艏摇、漂角和艏摇组合3种平面运动机构（Planar Motion Mechanism，PMM）运动的数值模拟，将横向力Y、艏摇力矩N、横倾力矩K的数值模拟结果与试验结果进行对比，并依照PMM试验的动力学方程，通过最小二乘法拟合和傅立叶积分，将数值模拟结果与试验结果的时历曲线进行分析处理，求得操纵水动力导数。研究结果表明：该方法用于数值模拟PMM运动是可行的；求得的水动力导数中Y′vvv，N′vvv误差略大，其余水动力导数误差均在15%以内。

体积力法；KCS船型；平面运动机构；水动力导数

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.010.html期刊网址：www.ship-research.com

引用格式：王慧婷，毕毅.基于体积力法的全附体KCS型船模PMM运动数值模拟［J］.中国舰船研究，2016，11（4）：29-37，66.

WANG Huiting，BI Yi.Numerical simulation on planar motion mechanism of KCS ship model with a body-force propeller mode［lJ］.Chinese Journal of Ship Research，2016，11（4）：29-37，66.

0　引　言

操纵性是船舶重要的航行性能，在船舶设计阶段需对操纵性进行预报。随着计算机及CFD技术的快速发展，采用计算机数值模拟方法预报船舶操纵性能已成为一种技术方法，而数值预报的关键是确定船舶操纵运动方程中的水动力导数。目前常用的有拘束模试验和数值计算2种方法，其中拘束模试验精度较高，但试验过程繁杂，需耗费大量的人力、物力，而数值计算则具有很多优点，如计算效率高、可以获得流场细节等，目前已获得较快的发展。

针对水动力导数的数值求解，最为常用的是数值模拟船舶平面运动机构（Planar Motion Mechanism，PMM），通过对计算中的时历曲线进行分析得到。目前，国内外学者对这方面均做了一定的研究。Broglia等［1］对KVLCC2船模进行了考虑自由面影响的纯横荡运动模拟，同时，Broglia等［2］数值模拟了带桨、舵的KVLCC1&2船的纯横荡和纯艏摇运动；Tyagi和Sen［3］利用RANS方程对2种典型AUV的斜拖运动进行了研究；Sakamoto等［4］和Guilmineau等［5］对光体DTMB 5415船模进行了PMM运动模拟；Miller［6］对光体和全附体的DTMB 5415船模均进行了PMM运动数值模拟，结果表明全附体所得结果误差较小。国内学者刘山［7］和程捷等［8］以光体DTMB 5415船模为研究对象，模拟了纯横荡和纯艏摇运动，并求得了相应的水动力导数；杨路春等［9］模拟了SUBOFF主艇体的平面运动，并求解了水动力导数；楼鹏宇［10］和石爱国等［11］均对限制水域中船舶的PMM运动进行了数值模拟。

然而，上述研究中均没有真实地模拟船模PMM的试验，有些未考虑自由面及运动过程中船模姿态变化的影响，有些未考虑附体的影响而只对光体船模进行了计算。即便考虑了桨、舵，因螺旋桨采用的是实体建模的方法，计算工作量较大，周期较长。体积力法［12-13］的计算效率较高，能反映螺旋桨作用，可以预报流场信息，但目前将该方法应用于船模PMM运动数值模拟的研究还较少。

针对以上研究现状，本文将基于star-ccm+平台，采用体积力法，对全附体KCS型船模进行斜航、纯艏摇、漂角和艏摇组合这3种PMM运动数值模拟，并考虑自由液面兴波和航行姿态变化的影响，测得船模运动中所受的横向力、艏摇力矩及横倾力矩，将计算结果与试验结果进行对比分析，以获得相应的水动力导数。

1　数值计算模型

1.1控制方程

对于雷诺平均后的不可压缩粘性流问题，采用的连续性方程和动量方程如下：

式中：ui为平均速度分量；p为平均压力；ρ为流体质量密度；μ为流体分子粘性系数；为

雷诺应力项。式（2）即为雷诺平均Navier-Stokes （Reynolds Averaged Navier-Stokes，RANS）方程。

1.2湍流模型

当求解分离和带有复杂二次流特征的流动时，Realizable k-ε模型优于标准k-ε模型，因此，采用Realizable k-ε湍流模型来封闭RANS方程。

Realizable k-ε湍流模型输运方程为：

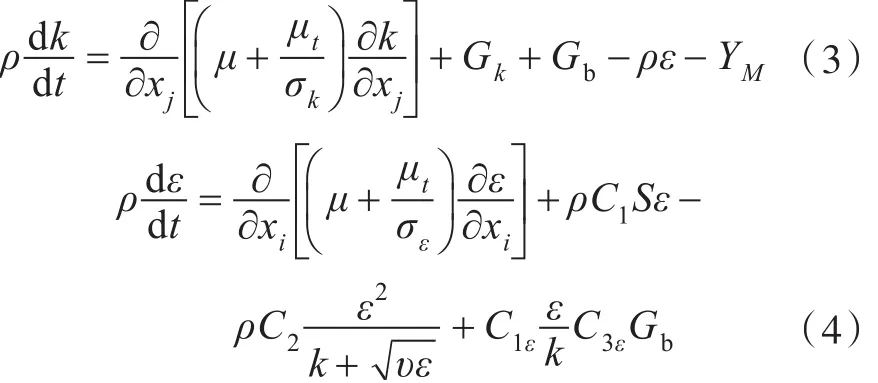
1.3体积力源项方程

采用基于势流升力面理论的涡格法，产生符合桨叶边界条件的体积力，将其作用在螺旋桨区域网格上，施加推力和扭矩以代替真实的螺旋桨表面载荷。相关公式如下：

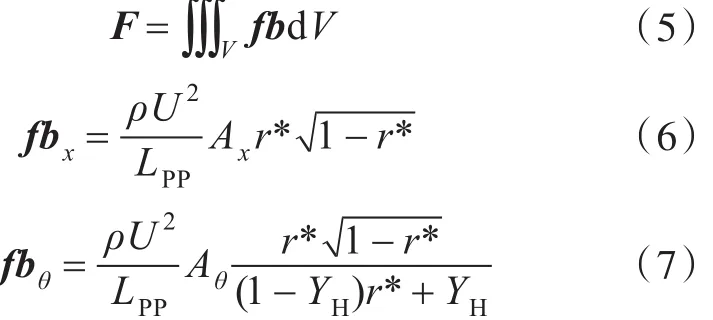
其中：

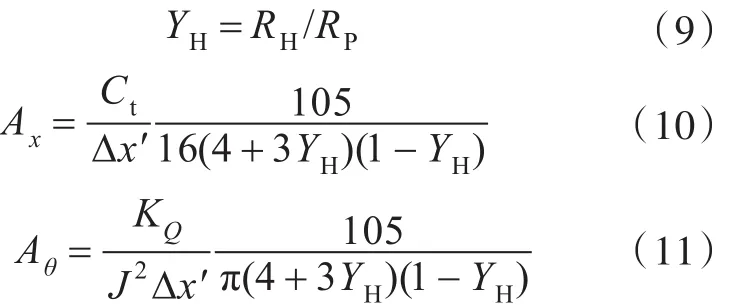
式中：Ct=2T/（ρU2πRp），为一种无量纲推力系数；KQ=Q/ρn2DP5，为转矩系数，其中n为螺旋桨转速；DP=2RP，为螺旋桨直径；r1为螺旋桨区域内任意一点到螺旋桨轴线的距离；RP和RH分别为螺旋桨半径和桨毂半径；LPP为船体垂线间长；Δx′=Δx/LPP，为桨毂厚度与船体垂线间长之比；J=Va/nDP，为螺旋桨进速系数，其中Va表示螺旋桨进速。

螺旋桨采用体积力法，即运用描述型体积力模型代替真实螺旋桨作用，此时，体积力模型中螺旋桨的作用区域如图1所示。 Kt，KQ取自Simman 2014中KCS船螺旋桨敞水试验结果。螺旋桨转速n与试验中相同，在star-ccm+软件中计算螺旋桨推力T和转矩Q时，需在螺旋桨作用区域前设定一虚拟的静流盘面，该盘面上的平均速度作为用体积力法计算时的进流速度，船尾流场的不均匀性体现在虚拟盘面平均速度上。

图1　螺旋桨作用区域Fig.1　The operational zone of propeller

2　计算对象及工况

2.1研究对象

本文以船舶操纵预报方法验证与确认专题讨论会Simman 2014中的基准算例作为参考，选取深水中带全附体的KCS型船模为研究对象。模型缩尺比为52.667，主要参数见表1。

2.2PMM运动计算模型

对KCS型船模进行斜航、纯艏摇、漂角和艏摇组合这3种PMM运动。船模运动方式定义如图2所示。

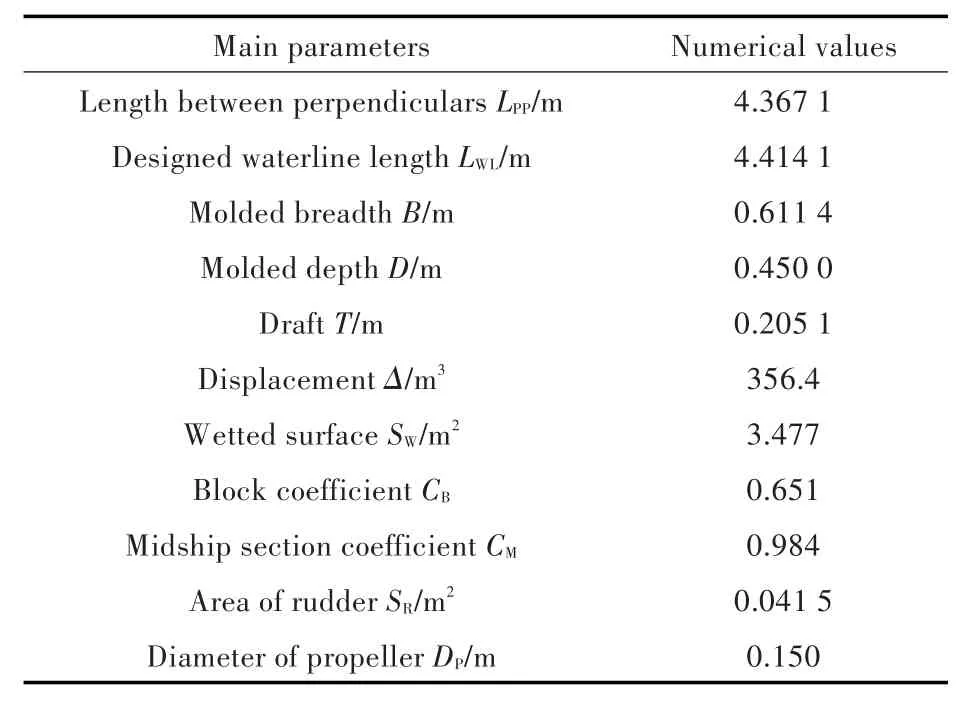
表1　KCS型船模主要参数Tab.1　Main parameters of the KCS model

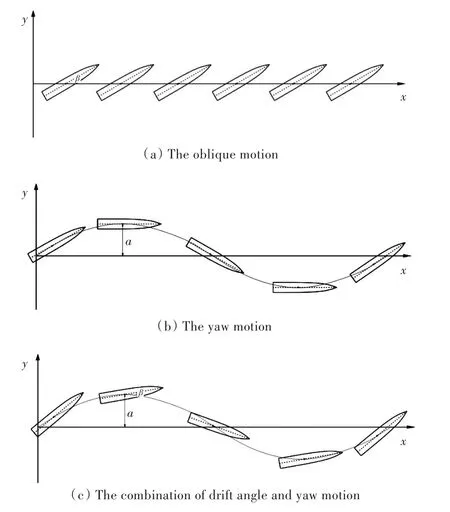
图2　船模运动方式Fig.2　Motion mode of ship model

运动中，重点分析船模所受的横向力Y，艏摇力矩N及横倾力矩K，其无因次化形式为：

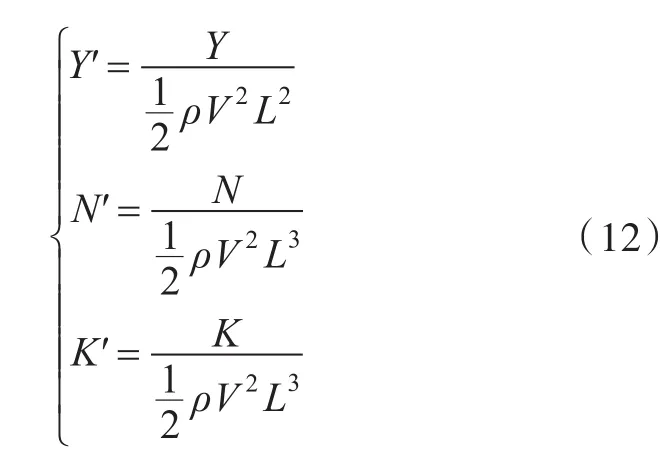
式中：V为航速；L为船长。

2.2.1斜航运动计算模型

斜航运动中，其运动表达示为

式中：r为角速度；v为横向速度；β为漂角。

船模所受水动力可表达为

对计算所得的水动力进行无因次化，将无因次水动力随无因次横向速度v′的变化曲线采用最小二乘法进行拟合，即得Yv′，Yvvv′，Nv′，Nvvv′，Kv′，Kvvv′。

2.2.2纯艏摇运动计算模型

纯艏摇运动中，其运动表达示为

其中：a为幅值；ψ0为艏向角幅值；ψ为艏向角；ω为角频率。

在船体坐标系下，水动力表达式为

以横向力Y为例，将运动表达式代入，其无量纲化形式为

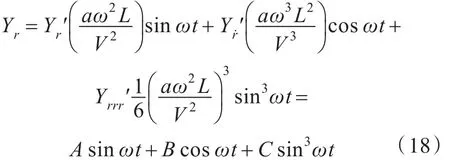
对船模运动中所受的无因次水动力曲线进行拟合得到各系数项A，C，再通过不同幅值a时的运动模拟结果对A和C进行二次拟合，直线斜率即为Yr′，Yrrr′。同理，可得Nr′，Nrrr′，Kr′，Krrr′。因此，对船模进行3个不同幅值下的纯艏摇运动，以求得相应的水动力导数。

2.2.3漂角和艏摇组合运动计算模型

漂角和艏摇组合运动中，其运动表达式为

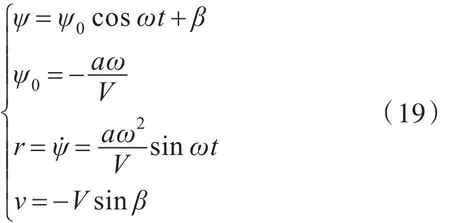
在船体坐标系下，水动力表达式为

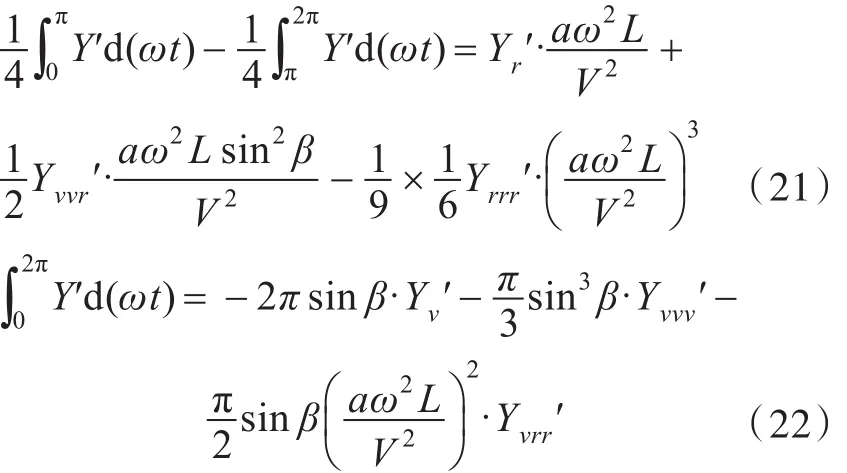
采用离散化函数积分形式计算式（21）和式（22）左边的积分值，代入已求得的Yr′，Yrrr′，Yv′，Yvvv′中，即可得到和。同理，可得Nv′

vr，，，。因此，漂角和艏摇运动选取一个状态下的运动即可求得相应的水动力导数。

2.3计算域及边界条件

采用矩形计算域，斜航运动时，在入流面给定一垂直于入流面的来流，船模与来流方向成一定的角度保持不动，即采用相对运动的方式使船模实现指定漂角下的斜航运动；纯艏摇、漂角和艏摇组合运动时，船模在水中做相应的运动。计算域的大小和入流面、出流面的位置由船长L确定，通常，须保证计算区域在船前不小于1倍船长，在船后和左、右两侧不小于2倍船长。如船模在深水中运动，下边界距船模应不小于2倍船长，船模计算域如图3所示。

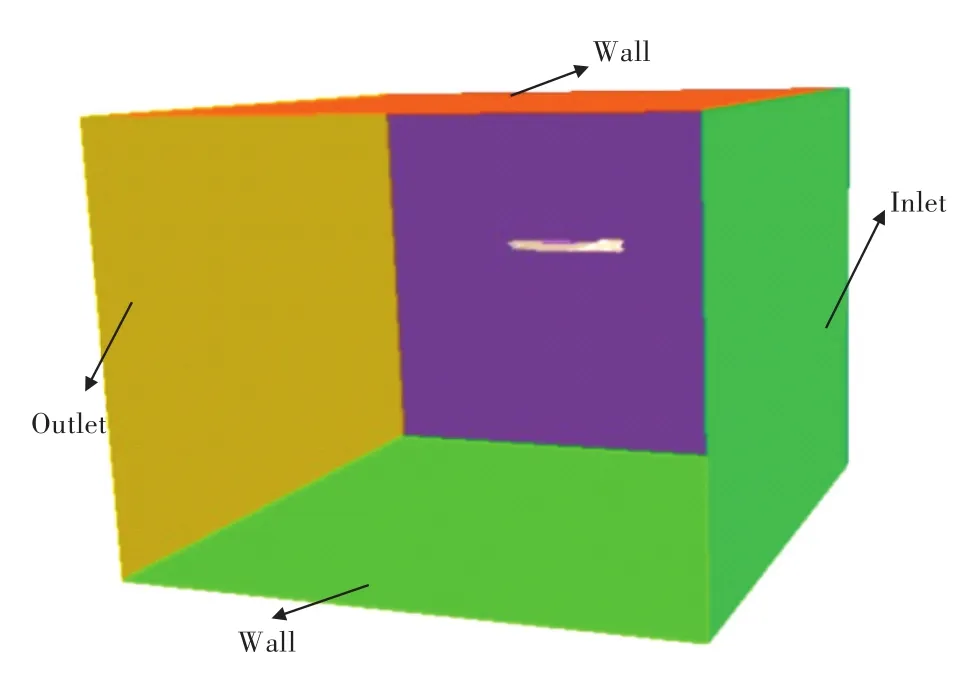
图3　船模计算域Fig.3　Computational domain of ship model

边界条件的设置如下：

1）入流面：速度入口，当船模做纯艏摇、漂角和艏摇组合运动时，来流速度为0 m/s。

2）出流面：压力出口，自由液面以上为标准大气压，以下设置为静水压力。

3）船模表面：无滑移壁面。

4）上、下、左、右外边界：同入流面。

2.4网格划分

数值模拟中所使用的网格均为全六面体非结构化网格，对运动产生的兴波区域、自由面附近以及船首、尾部分进行加密。船模首、尾部网格划分如图4所示，计算域的网格划分如图5所示，斜航运动时将船模及周围加密区网格旋转相应的角度，形成对应的计算域网格。

图4　船首、尾部网格划分Fig.4　Grid partition on the bow and stern

图5　计算域的网格划分Fig.5　Grid partition on the computational domain

2.5网格密度的选取

为分析不同网格密度对计算结果的影响，以漂角β=-8°时的斜航运动为例，对4种不同网格密度下的计算域进行计算，并对结果进行对比分析。选取计算域x轴方向为（-1.5～2.5）L，y轴方向为（-2.5～2.5）L，z轴方向为（-2.0～1.0）L。固定边界层的总厚度为0.02 m，通过改变层数来改变第1层网格到船体表面的距离，进而影响着网格密度，网格具体情况如表2所示。

由表2可知，随着边界层层数的增加，计算所得水动力趋于稳定。当边界层层数为10层时，已在稳定范围之内，因此，本文采用此网格密度下的计算域进行计算。

3　数值模拟结果及分析

为验证所使用方法及计算结果的正确性，将结果与 Simman 2014中“KCS PMM tests with appended hull，FORCE 2009”试验结果进行了对比。各PMM运动数值模拟计算工况如表3所示。

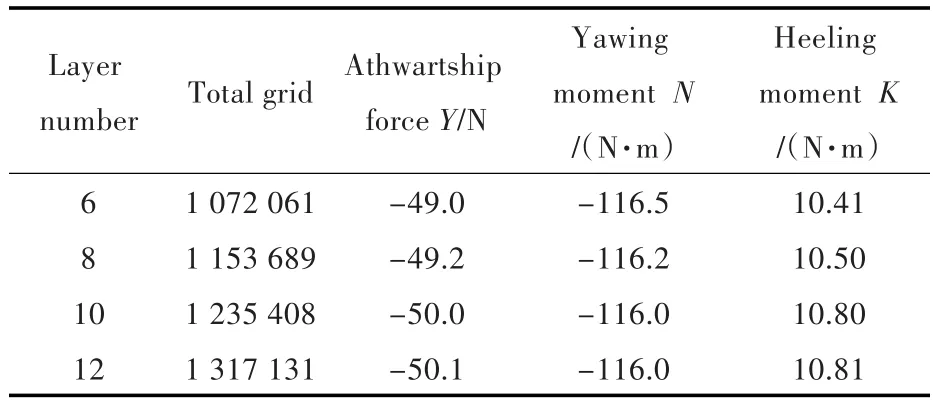
表2　不同网格数量下的水动力比较Tab.2　Comparison of hydrodynamics under different grid quantities

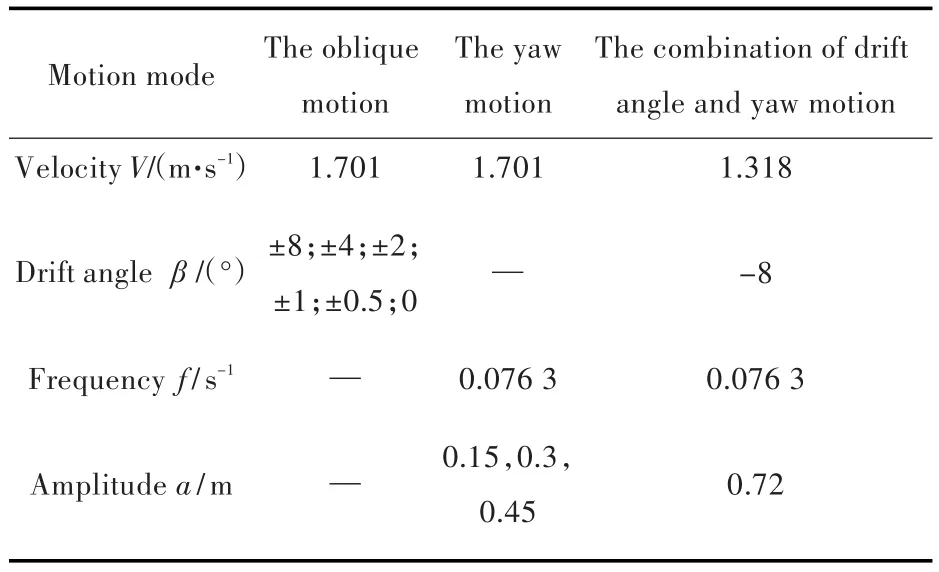
表3　各PMM运动数值模拟计算工况Tab.3　Calculation condition of planar motion's numerical simulation

3.1斜航运动计算结果

通过数值模拟，计算得到船模所受的无因次水动力随漂角β的变化曲线如图6所示。从图中可以看出，各漂角下横向力的计算结果与试验结果吻合较好；对于艏摇力矩，计算结果与试验结果有一定的误差，因即使横向力计算与试验结果误差很小，反映到艏摇力矩上误差也会增大，因此图中所示结果差距是可以接受的；而对于横倾力矩，计算结果与试验结果相差不大，且计算结果曲线与试验结果曲线的变化趋势非常相似。

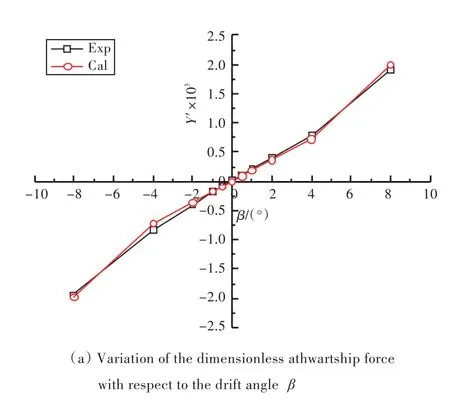
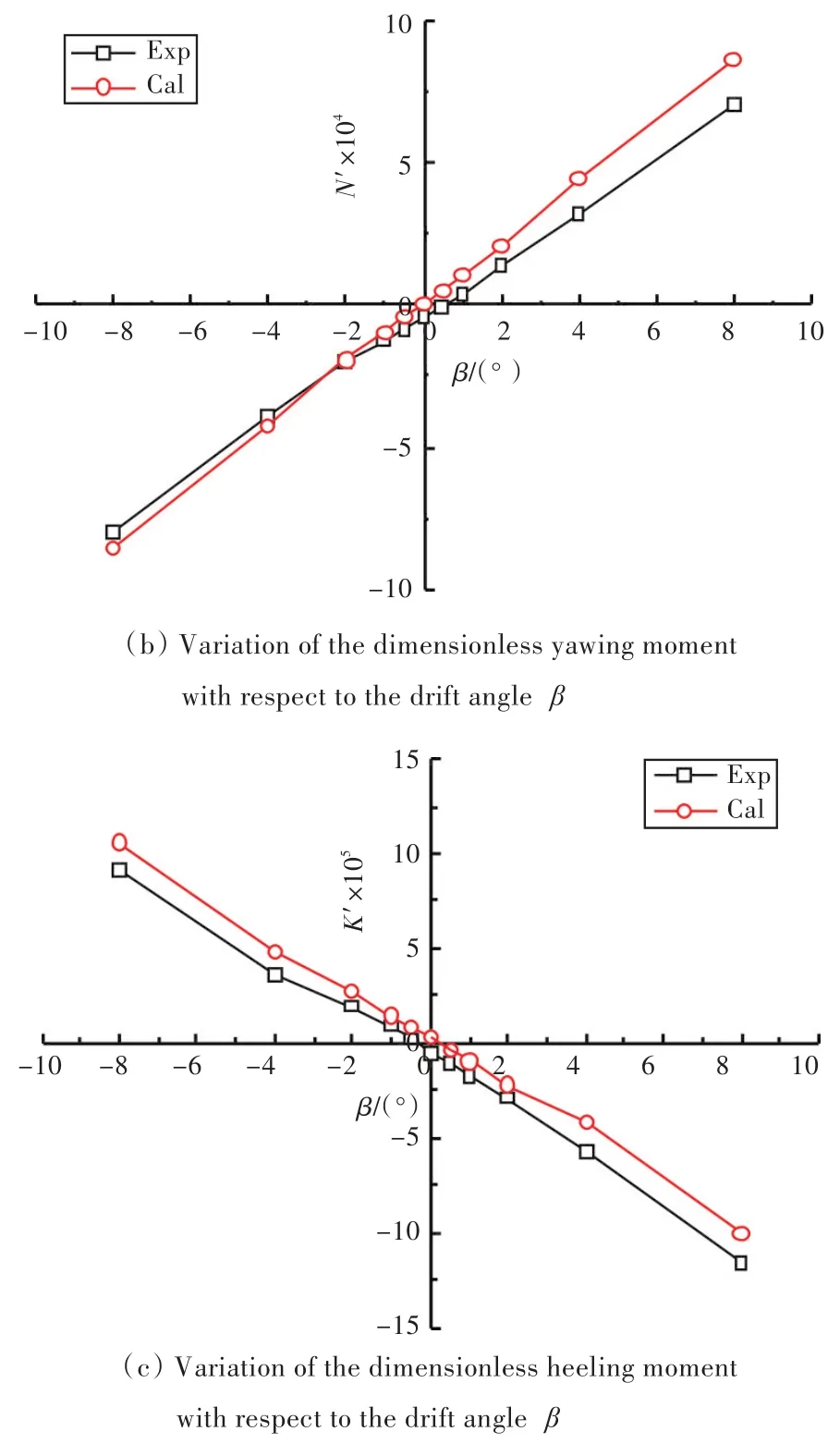
图6　船模所受无因次水动力随漂角β变化曲线Fig.6　Variation of the dimensionless hydrodynamics with respect to the drift angleβ

根据无因次水动力随漂角 β变化的曲线，采用最小二乘法求得的水动力导数如表4所示。由表中可看到，高阶导数的误差略大，其余水动力导数误差均在20%以内。

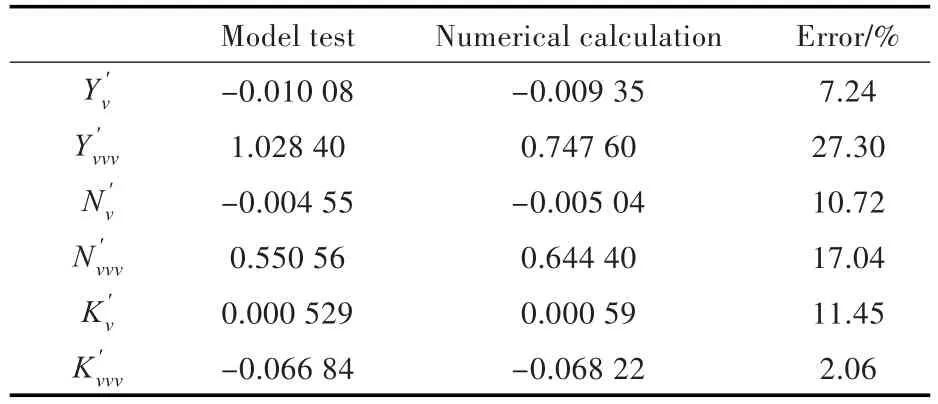
表4　斜航运动中水动力导数计算结果Tab.4　The calculation results of the hydrodynamic derivatives in the oblique motion

运动中，当漂角β为-2°和-4°时，船体周围兴波图如图7所示。由图可知：随着漂角的增加，船体两侧的兴波越来越不对称，背流面散出的波形距离船体越来越远，较好地反映出运动中船体周围波形的变化规律。

图7　漂角为-2°和-4°时船体周围兴波图Fig.7　The free surface wave patterns around the hull in the static drift atβ=-2°andβ=-4°

3.2纯艏摇运动计算结果

当船模运动稳定后，选取一个周期内的数值模拟结果进行研究。振幅为0.15，0.3，0.45 m时船模所受的无因次水动力时历曲线分别如图8～图10所示。分析可得，船体做简谐运动时，所受的力与力矩均应符合简谐规律。由图可知，计算结果较好地体现出了简谐规律，而试验结果则存在着一定的波动，这有可能来源于试验中测量力装置的量程、安装方式及数据处理方法等，且K/N≈0.05，横倾力矩较小，试验不易测得。横向力、艏摇力矩的试验与计算结果吻合良好，而横倾力矩的则略有误差，这是因为数值计算中采用RANS控制方程对平均时间内的压力和速度进行描述，不能较为精细地捕捉到船体周围的涡产生及脱落等非定常现象，会对计算结果带来一定的影响。横向力、艏摇力矩和横倾力矩的幅值均随运动幅值的增加而增大。

根据无因次水动力时历曲线求得的水动力导数如表5所示。各旋转导数误差均在15%以内。

3.3漂角和艏摇组合运动计算结果

图8　振幅为0.15 m时船模所受无因次水动力时历曲线Fig.8　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.15 m

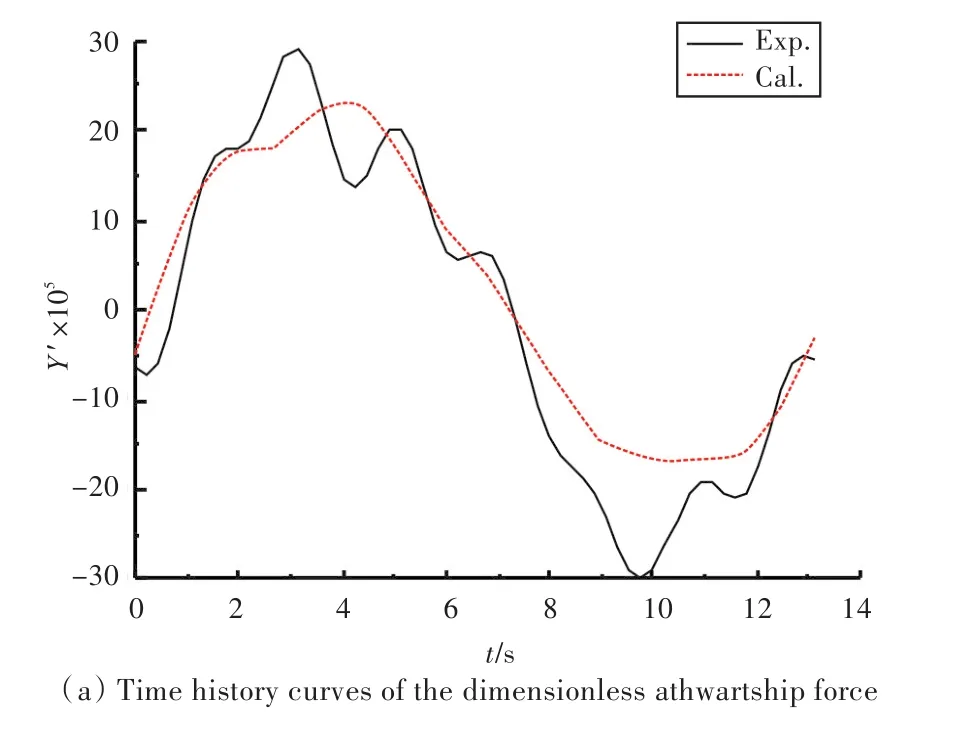
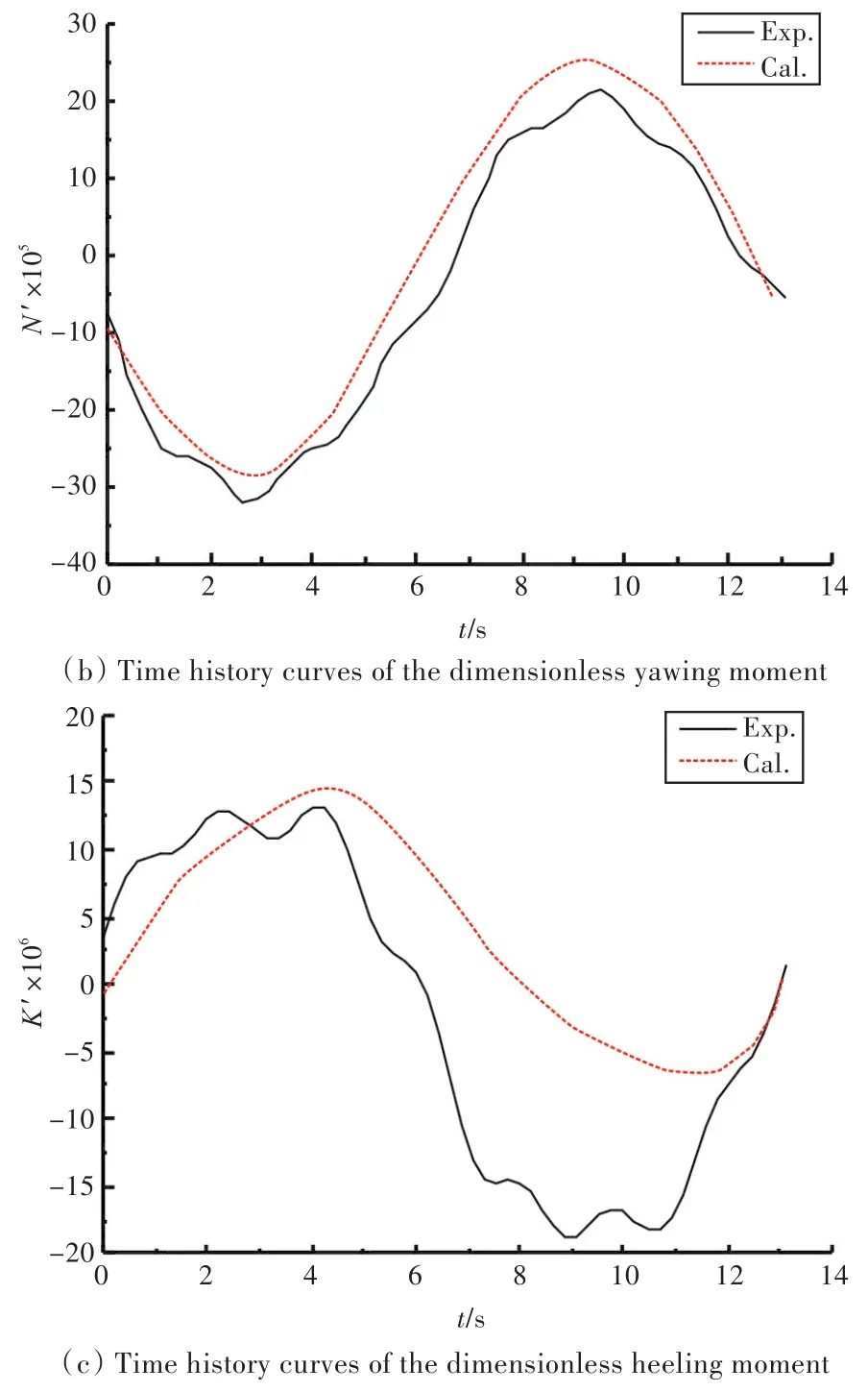
图9　振幅为0.3 m时船模所受无因次水动力时历曲线Fig.9　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.3 m

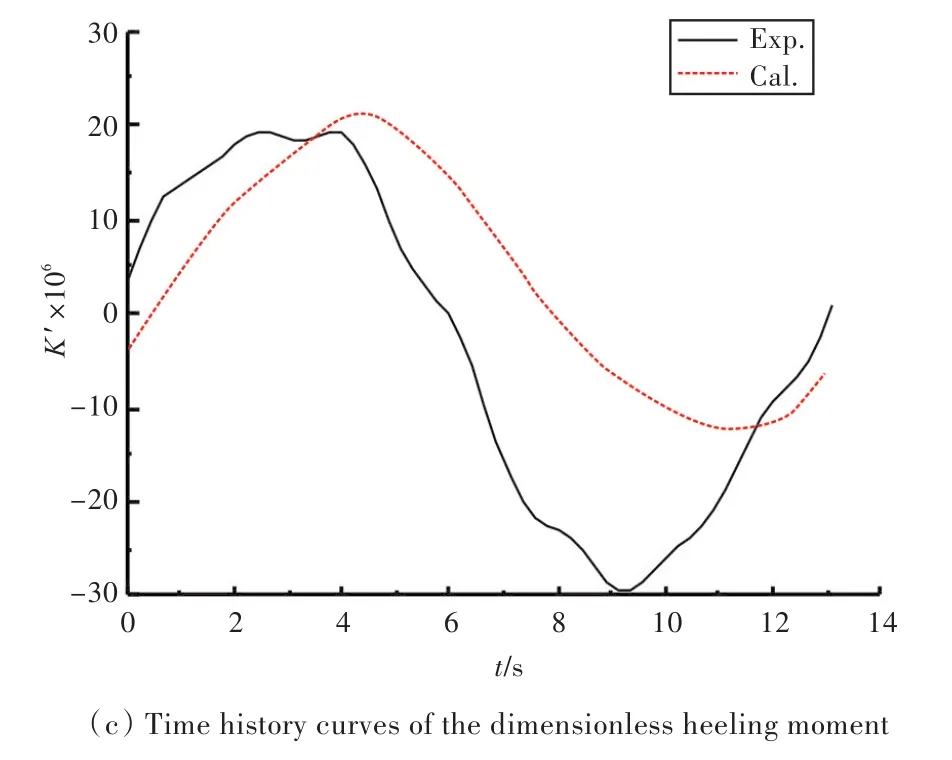
图10　振幅为0.45 m时船模所受无因次水动力时历曲线Fig.10　Time history curves of the dimensionless hydrodynamics when the amplitude is 0.45 m

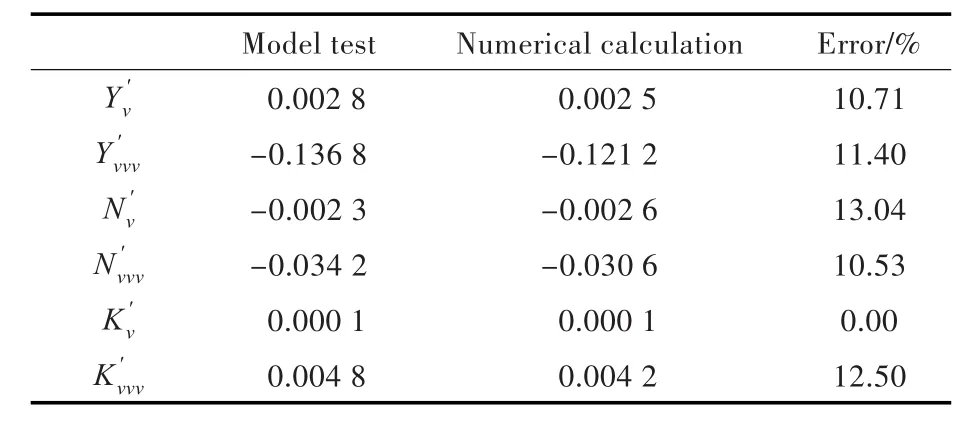
表5　纯艏摇运动中水动力导数计算结果Tab.5　The calculation results of the hydrodynamic derivatives in the yaw motion

船模运动稳定后，选取一个周期内的数值模拟结果进行分析。船模所受的无因次水动力时历曲线如图11所示。由图可知：对于横向力，在前半个周期内，试验和计算结果均先增大后减小，再增大；艏摇力矩的试验与计算结果吻合较好，符合简谐规律；横倾力矩的计算与试验结果相差略大，其原因与纯艏摇运动中横倾力矩的试验与计算结果误差略大相同。

根据无因次水动力曲线求得的水动力导数如表6所示。耦合导数误差均在16%以内。

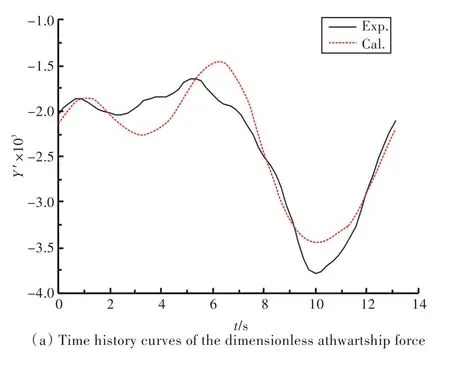
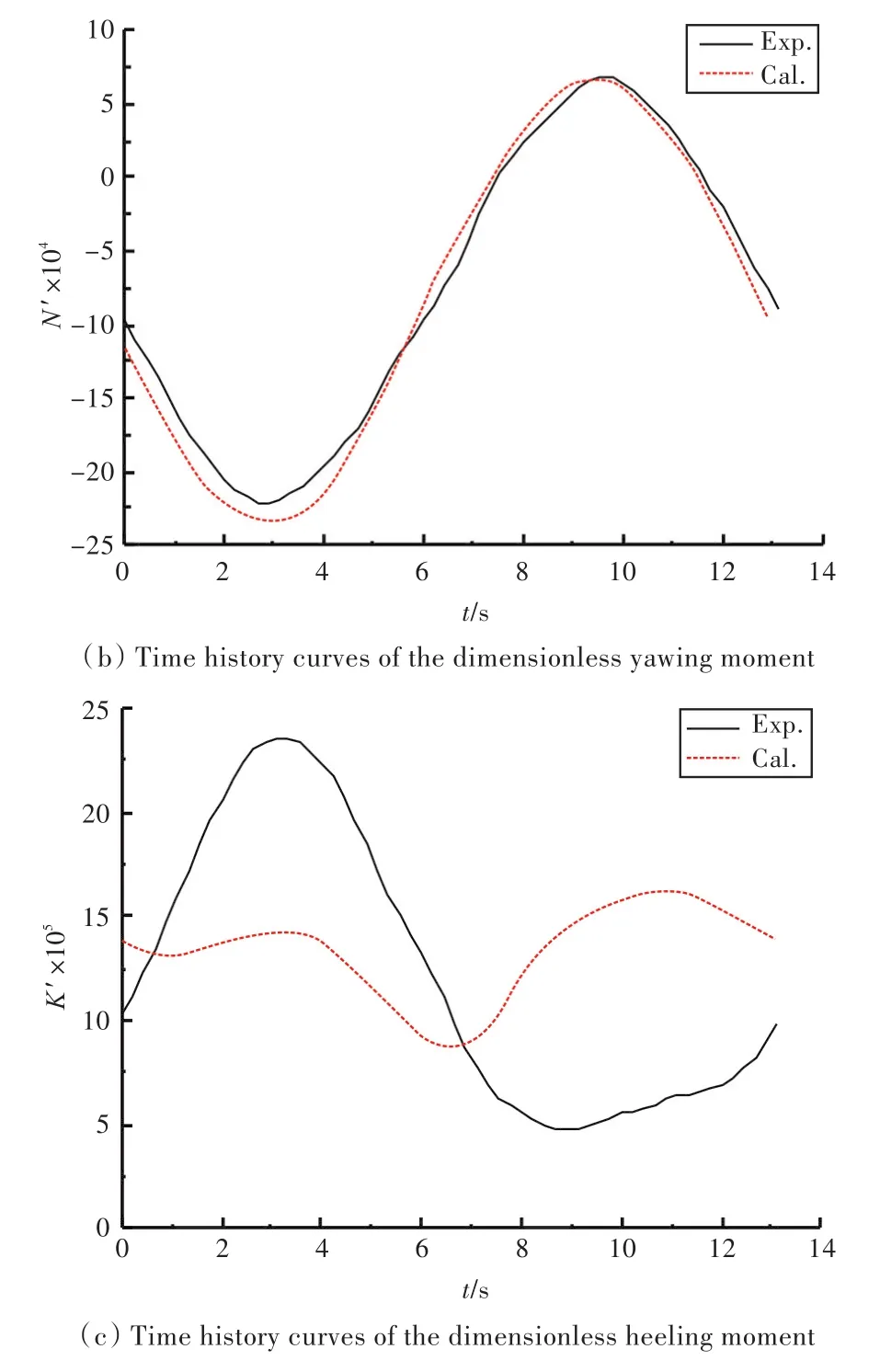
图11　船模所受无因次水动力时历曲线Fig.11　Time history curves of the dimensionless hydrodynamics

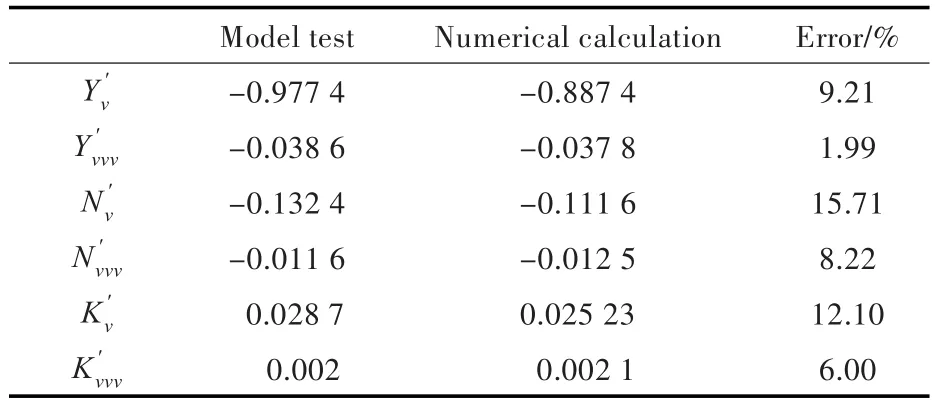
表6　漂角和艏摇组合运动中水动力导数计算结果Tab.6　The calculation results of the hydrodynamic derivatives in the combination of drift angle and yaw motion

4　结　语

本文基于star-ccm+软件平台，以全附体KCS船模为研究对象，应用体积力法模拟真实螺旋桨作用，开展了该船斜航、纯艏摇、漂角和艏摇组合的PMM运动模拟研究，获得了以下结论：

1）将体积力法应用到螺旋桨的处理上，大幅降低了网格数量，提高了计算效率。

2）研究的对象为全附体KCS型船模，且考虑了自由面兴波及运动中船模姿态变化这些条件的影响，更真实地模拟了PMM试验，采用理论分析方法求解的水动力导数误差在20%以内，提高了计算精度。

［1］ BROGLIA R，DI MASCIO A，AMATI G.Aparallel unsteady RANS code for the numerical simulations of free surface flows［C］//Proceedings of the 2nd International Conference on Marine Research and Transportation.Naples，Italy：［s.n.］，2007.

［2］ BROGLIA R，MUSCARI R，DIMASCIO A.Numerical simulations of the pure sway and pure yaw motion of the KVLCC-1 and 2 tanker［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［3］TYAGI A，SEN D.Calculation of transverse hydrodynamic coefficients using computational fluid dynamic approach［J］.Ocean Engineering，2006，33（5/6）：798-809.

［4］SAKAMOTO N，CARRICA PM，STERN F.URANS simulations of static and dynamic maneuvering for surface combatant［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s. n.］，2008.

［5］ GUILMINEAU E，QUEUTEY P，VISONNEAU M，et al.RANS simulations of a US Navy frigate with PMM motions［C］//Proceedings of SIMMAN 2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［6］MILLER R W.PMM calculations for the bare and appended DTMB 5415 using the RANS solver CFDSHIP-IOWA［C］//ProceedingsofSIMMAN2008 Workshop on Verification and Validation of Ship Maneuvering Simulation Methods.Lyngby，Demark：［s.n.］，2008.

［7］刘山.基于CFD技术数值模拟平面运动机构试验［D］.武汉：武汉理工大学，2012.

LIU Shan.Numerical simulation of planar motion mechanism test based on CFD technology［D］.Wuhan：Wuhan University of Technology，2012.

［8］程捷，张志国，蒋奉兼，等.平面运动机构试验的数值模拟［J］.水动力学研究与进展，2013，28（4）：460-464. CHENG Jie，ZHANG Zhiguo，JIANG Fengjian，et al. Numerical simulation of the planar motion mechanism tests［J］.Chinese Journal of Hydrodynamics，2013，28 （4）：460-464.

［9］杨路春，庞永杰，黄利华，等.潜艇PMM实验的CFD仿真技术研究［J］.舰船科学技术，2009，31 （12）：12-17.

YANG Luchun，PANG Yongjie，HUANG Lihua，et al.Study of the CFD approach to simulate PMM experiments of submarine［J］.Ship Science and Technology，2009，31（12）：12-17.

［10］ 楼鹏宇.限制水域中纯横荡运动船体水动力数值计算［D］.上海：上海交通大学，2012.

LOU Pengyu.Numerical calculation of the hydrodynamic forces on a ship in pure sway motion in restricted waters［D］.Shanghai：Shanghai Jiao Tong University，2012.

［11］石爱国，闻虎，李理，等.船舶浅水水动力导数的数值计算［J］.中国航海，2011，34（3）：69-73，83.

SHI Aiguo，WEN Hu，LI Li，et al.Computation of hydrodynamic derivatives for ships in shallow water［J］.Navigation of China，2011，34（3）：69-73，83.

［12］吴召华，陈作钢，代燚，等.基于体积力法的船舶回转运动水动力数值研究［J］.中国舰船研究，2013，8（4）：12-19.

WU Zhaohua，CHEN Zuogang，DAI Yi，et al.Numerical study of hydrodynamic force on ships in turning motion based on a body-force propeller model［J］. Chinese Journal of Ship Research，2013，8（4）：12-19.

［13］吴召华，陈作钢，代燚.基于体积力法的船体自航性能数值预报［J］.上海交通大学学报，2013，47 （6）：943-949.

WU Zhaohua，CHEN Zuogang，DAI Yi.Numerical prediction of self-propulsion with a body-force propeller model［J］.Journal of Shanghai JiaoTong University，2013，47（6）：943-949.

Numerical simulation on planar motion mechanism of KCS ship model with a body-force propeller model

WANG Huiting，BI Yi
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

In order to solve the ship maneuvering hydrodynamic derivatives efficiently and accurately，full-appendage KCS ship model is taken in this paper as the studying object.Based on RANS equation and VOF model，a descriptive body-force model is established to represent real propellers on the star-ccm+；the influences of the free surface wave and motion attitudes change on hydrodynamic are taken into account.The oblique motion，the yaw motion，the combination of yaw and drift angle motion on Planar Motion Mechanism（PMM）are simulated，and the athwartship force Y，the yawing moment N，and the heeling moment K are also acquired.The simulation results are then compared with the actual test results:according to the dynamics equation of PMM test，the time history curves of numerical and experimental results are analyzed with least-squares fitting and Fourier integral，where the hydrodynamic derivatives of manipulation are finally obtained.The results demonstrate the feasibility of the proposed method in PMM simulation，though the errors ofY′vvvandN′vvvare slightly larger，the errors of remaining hydrodynamic derivatives are all below 15%.

body-force propeller model；KCS ship model；Planar Motion Mechanism（PMM）；hydrodynamic derivatives

U661.3

A

10.3969/j.issn.1673-3185.2016.04.005

2015-10-23网络出版时间：2016-7-29 9:45

水动力学重点基金资助项目（9140A14030712JB11044）；海军工程大学自然科学基金资助项目（435517J4040）

王慧婷（通信作者），女，1990年生，硕士。研究方向：舰船流体动力性能。

E-mail：whut_wht@163.com

毕毅，男，1963年生，硕士，副教授。研究方向：舰船操纵性。E-mail：kpzc2002@163.com