基于指数分布的随机性平面曲线可视化研究
2016-09-02彪佛山科学技术学院数控技术研究室广东佛山528000
卢 彪佛山科学技术学院数控技术研究室,广东佛山 528000
基于指数分布的随机性平面曲线可视化研究
卢 彪
佛山科学技术学院数控技术研究室,广东佛山 528000
指数分布常被用来描述世界上实体的寿命,从广义上讲,也可以用来描述能量的耗散。本文采用AutoCAD.NET的二次开发技术把二维平面点的可视化问题从非随机点扩展到随机点,并使用指数分布尝试模拟质点运动轨迹中受到某场的作用而产生能量的耗散。
指数分布;二维随机平面点;可视化;AutoCAD.NET
在以往的曲线的可视化的研究方面,大多数都集中在确定性的,随机性、模糊性的可视化研究比例却很少。本文使用AutoCAD.NET技术,对基于指数分布的二维随机平面点可视化问题进行了初步的探讨研究,在工业产品图案设计方面具有一定的参考价值。
1 指数分布
指数分布是数理统计中最重要的连续性分布之一,它是一个随机变量只可能取非负实数的分布,所以指数分布常被称为“寿命”分布.诸如电子原件使用寿命,动物的寿命,通话时长等都可以假定服从指数分布.[1]


指数分布的分布函数如下:

指数分布的数学期望与方差如下:

2 AutoCAD.NET二次开发及其可视化技术
众所周知,对AutoCAD进行二次开发用到的主要工具有ObjectARX、VBA和Lisp,但它们的优缺点是显而易见的:ObjectARX功能强大,编程效率高,但它的缺点是编程者必须掌握VC++,而这门语言非常难学;VBA和Lisp虽然简单易上手,但它们对于开发大型的程序好像无能为力。而.NET则结合了VC++功能强大与VBA易用的特点,可以非常快速地开发出功能强大的AutoCAD程序[3]。因此,在综合各种二次开发工具的特点后,决定使用AutoCAD.NET进行二次开发[3-15]。
先简单介绍AutoCAD数据库的基础知识。AutoCAD数据库至少包含9个符号表(块表、层表、文字样式表、线型表、视图表、UCS表、视口表、注册应用程序表、标注样式表)。一个表可能包含多条记录,也可能不包含任何记录。
实体包含在块表记录中,要创建一个图形对象,需要遵循下面的基本步骤:
1)得到创建对象的图形数据库。
2)在内存中创建实体类的一个对象。
3)打开图形数据库的块表。
4)打开一个存储实体的块表记录(通常绘图都在模型空间进行),所有模型空间的实体都存储在块表的“模型空间”记录中。
5)将该对象添加到块表记录中。
把实体存储在“模型空间”记录中后,打开AutoCAD,装载被写入程序的dll文件,然后就能在我们常见的AutoCAD模型空间中看到我们编写的实体了。
3 程序结构
程序结构总结起来,可以分为五步(如图1)。
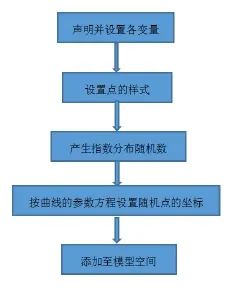
图1 程序结构图
4 图形的生成
根据不同曲线的参数方程,生成的图形也有所不同。1)X方向为指数分布Y方向为均匀分布。
此时并不构成曲线,图形如图2。

图2 X方向为指数分布Y方向为均匀分布
X方向为均匀分布Y方向为指数分布的图形类似,不再赘叙。
2)X方向为指数分布Y方向为指数分布。
此时并不构成曲线,图形如图3。

图3 X方向为指数分布Y方向为指数分布
3)圆。
圆的参数方程为:

生成的图形如图4。

图4 圆
4)椭圆。
椭圆的参数方程为:

生成的图形如图5。

图5 椭圆
5)双曲线。
双曲线的参数方程为:

生成的图形如图6。

图6 双曲线
6)心形线。
心形线的极坐标方程为:

生成的图形如图7。

图7 心形线
7)阿基米德螺旋线。
阿基米德螺旋线的极坐标方程为:

生成的图形如图8。

图8 阿基米德螺旋线
8)伯努利双纽线。
伯努利双纽线的极坐标方程为:

生成的图形如图9。

图9 伯努利双纽线
9)三叶玫瑰线。
三叶玫瑰线的极坐标方程为:

生成的图形如图10。

图10 三叶玫瑰线
5 结论与展望
本文展示了基于指数分布的一系列常见平面曲线的二维随机平面点的图案,对工业产品图案设计方面具有一定的参考价值。笔者将在后续的研究中,继续挖掘其中各细节的知识点,期待能对图形可视化的应用领域做出一点贡献。
[1]文小波.指数分布在截尾数据下参数的区间估计[J].佳木斯大学学报,2014,32(6):960-961.
[2]吴松飞,刘晓.双截尾指数分布的统计性质[J].绵阳师范学院学报,2012,31(2):13-15.
[3]曾洪飞,卢择临,张帆.AutoCAD VBA&VB.NET开发基础与实例教程[M].2版.北京:中国电力出版社,2008.
[4]李冠亿.深入浅出AutoCAD.NET二次开发[M].北京:中国建筑工业出版社,2012.
[5]李世国.AutoCAD高级开发技术:ARX编程及应用[M].北京:机械工业出版社,1999.
TH12
A
1674-6708(2016)168-0129-03
卢彪,在读硕士研究生,研究方向为AutoCAD二次开发。
