追及问题中错解分析

安徽省太和中学　孙恒启

追及问题中错解分析

安徽省太和中学孙恒启

在运动学中，追及问题是比较容易出错的，尤其在我们初学的时候，总是不经意间就陷入题目所设置的“陷阱”中。结合平时的学习，我们一起来探讨一下关于追及过程中匀减速直线运动的问题。

一、追及和相遇

1.定义：指同一时刻到达同一位置。

2.两个关系：一是相遇位置与各物体的初始位置之间存在一定的位移关系。若同地出发，则相遇时位移相等。二是相遇物体的运动时间也存在一定的关系：若物体甲、乙同时出发，运动时间相等；若甲比乙早出发Δt，则运动时间关系为t甲=t乙+Δt。

要使两物体相遇，就必须同时满足位移关系和运动时间关系。

3.一个条件：两者速度相等，这往往是物体间能否追上、追不上或（两者）距离最大、最小的临界条件，也是分析判断的切入点。

例1甲、乙两辆汽车在一条平直的公路上同向行驶，甲在前，乙在后，甲的速度为v1=8 m/s，乙的速度为v2=16 m/s，当两车相距为L=8 m时，甲车突然以a1=2 m/s2的加速度做匀减速运动，同时乙车立即刹车，为了避免两车相撞，乙车的加速度至少应为多少？

分析解答本题时要注意相遇的条件：当乙车追上甲车时，若两车的速度恰好相等，则乙车刹车时加速度为最小值。再根据位移关系求出时间，根据速度相等条件求出加速度。

解设乙车刹车时加速度的最小值为a2，当乙车追上甲车且两车的速度恰好相等时，经过的时间为t，此时两车的速度为v，

根据位移关系，有s2-s1=L①，

对甲，根据运动学公式，

对乙，根据运动学公式，

有s2=v2t-③，

又因为v=v1-a1t④，

v=v2-a2t⑤，

由①、②、③、④、⑤并代入数据，解得：a2=6 m/s2。

乙车的加速度至少为6 m/s2。

点评本题是追及问题，关键是寻找临界条件。

拓展1对于例1，若L=16 m，其他条件不变，则乙车的加速度至少应为多少？

解答过程如例1，只需将L=8 m换成L=16 m，即可求得a=4 m/s2，即乙车的加速度至少为4 m/s2。

拓展2对于例1，若L=32 m，其他条件不变，则乙车的加速度至少应为多少？

解答过程如例1，只需将L=8 m换成L=32 m，即可求得a=3 m/s2，即乙车的加速度至少为3 m/s2。

仔细分析不难发现，拓展2的答案不妥。结合拓展1分析可知，对甲而言，4 s时已经停了，对乙来说，则需要s方能停止。究其原因，是出现了反向加速运动的情况，与实际情况不符，不符合题意。

对于拓展2的正确解答：

设乙车刹车时加速度的最小值为a2。当乙车追上甲车速度恰好相等时，经过的时间为t，此时两车的速度为v。

根据位移关系，

有s2-s1=L①，

对甲，根据运动学公式，

有v21=2a1s1②，

对乙，根据运动学公式，

有v22=2a2s2③，

根据图像亦可得到同样的结论。

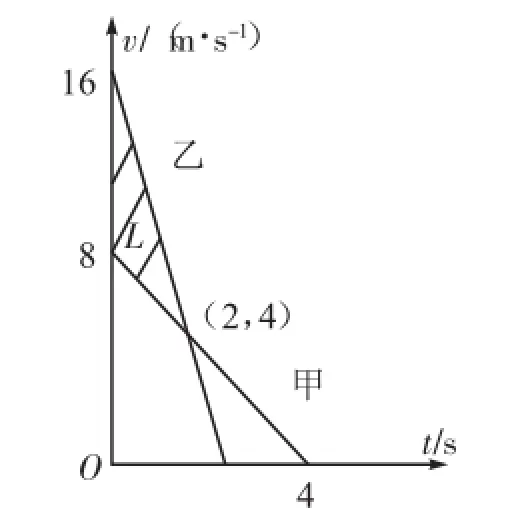
例1图

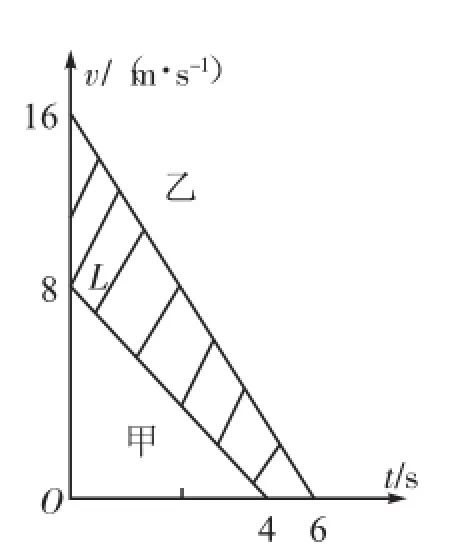
拓展2图

分析如图，例1图所示阴影部分的面积表示L=8 m，速度相等时刚好相遇，如果乙的加速度小些，则相遇时乙的速度仍大于甲的速度，不符合题意，即乙车的加速度至少为6 m/s2。

拓展1图所示阴影部分的面积表示L=16 m，速度相等且为零时刚好相遇，如果乙的加速度小些，则乙追上甲时乙的速度仍大于0，而此时甲刚好停止，不符合题意，即乙车的加速度至少为4m/s2。

拓展2图所示阴影部分的面积表示L=32 m，甲的速度为0时乙不可能追上甲，因此必须当乙刚好追上甲时速度也是0才符合题意，即乙车的加速度至少为

如何利用追及中的“两关系、一条件”是避免错误的核心内容，被追及的物体做匀减速直线运动时一定要注意“停而复返”和“停而止”的问题，相信结合图像分析能使我们更充分地理解。通过下面的例题，再来感受一下这一思想的巧妙之处。

例2如图，A、B两物体相距为s=7 m，物体A在水平拉力和摩擦力的作用下，正以vA=4 m/s的速度向右匀速运动。而物体B此时的速度vB=10 m/s，方向向右，由于摩擦力的作用向右做匀减速运动，加速度为a=-2 m/s2，那么物体A追上物体B所用的时间为（）。

A.7 s B.8 s C.9 s D.10 s

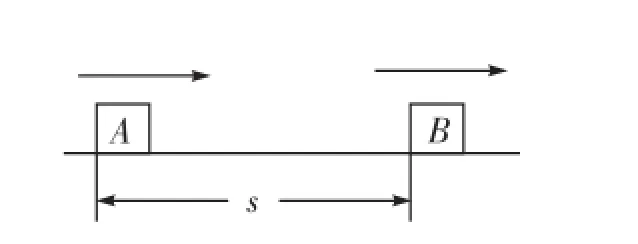
例2图

拓展对于例2，若改“由于摩擦力的作用”为“在外力和摩擦力的作用下”，其他条件不变则应选哪一项？

我们可以看到原题是“停而止”，而拓展则是“停而复返”，故答案分别为B和A。

通过这样的学习我们以后的学习中一定要注意多角度、多方法、多情景、多拓展地分析和解决运动学类的题目。◀