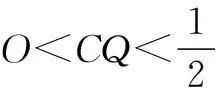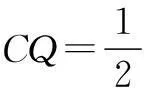浅析立体几何中动点问题的求解策略

周金波

(江苏省东台市三仓中学，224231)



浅析立体几何中动点问题的求解策略

周金波

(江苏省东台市三仓中学，224231)

近年来立体几何中有关“动点”求解问题不断地出现在各级各类试题中,现分类例说如下．

一、动中觅静

这里的“静”是指问题中的不变量或者是不变关系,动中觅静就是在运动变化中探索问题中的不变性．“静”只是“动”的瞬间,是运动的一种特殊形式,然而抓住“静”的瞬间,使一般情形转化为特殊情形,问题便迎刃而解．

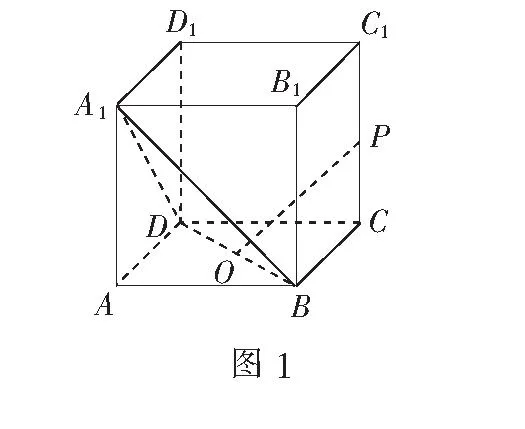
例1(2014年四川高考题)如图1,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是()

二、空间问题平面化

将立体几何中的问题转化成到一个平面上来考虑,再用平几知识解决问题，这是降维思想在立几问题中的常见策略．

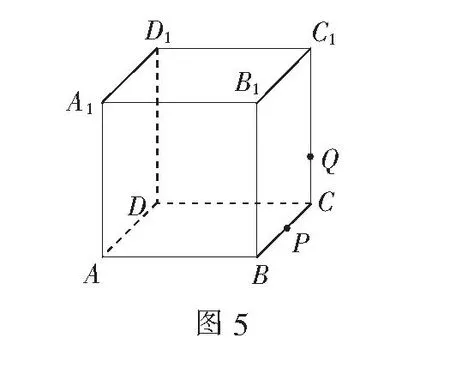
例2(2013年北京高考题)如图2,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,则点P到直线CC1距离的最小值是______.

略解取B1C1的中点E1,连结E1E、E1D1.过点P作PH∥E1E，交E1D1于H点,则PH∥CC1,所以点P到CC1的距离等于点H到CC1的距离,即为HC1,此时,问题便转化为在平面D1E1C1内来处理．

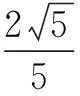
三、展开立体图为平面图

处理空间几何体侧面上某两点之间的最短距离问题,一般是将其侧面展开,化立体图为平面图,然后利用两点间线段长最短,求出最小值．

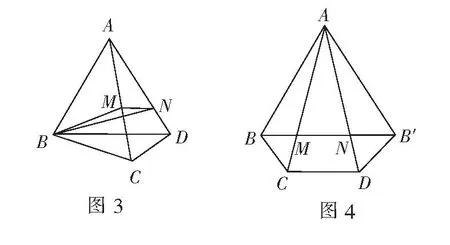
例3如图3，已知三棱锥A-BCD的底面是等边三角形,三条侧棱长都等于1,且∠BAC=30°,动点M、N分别在棱AC、AD上运动,求∆BMN周长的最小值．

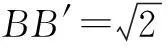
四、分析排除法

这种方法适用于选择题,根据题目选择支提供的信息,从特殊情况入手,逐一排除,直到选择正确的结果．