概率中的几个易错问题
2016-08-31李文东
李文东
(广东省中山纪念中学,528454)
概率中的几个易错问题
李文东
(广东省中山纪念中学,528454)
概率统计是新课标高中数学内容中的一个亮点,它替代了传统的数学应用题.然而对于概率的计算,许多同学都存在不少误区,究其原因,除了许多概率的计算需要用到排列组合的知识,读清楚题目表达的实际含意外,还需要对一些概率的概念的本质有一个清晰的把握.本文通过一些概率中的易错典型例题对概率易错问题进行辨析,希望能够让学生正确地理解并掌握运用,同时对教师的课堂教学也能起到一定的帮助作用.
一、概率中的顺序问题
例1一个盒子中有大小形状相同的10个球,其中有7白球,3个黑球,分别求下列事件的概率:
(1) 从中有放回的依次取出两球,取出的两球颜色不同;
(2) 从中无放回的依次取出两球,取出的两球颜色不同;
(3) 从中无放回的依次取出两球,第一次取出的是黑球,第二次取出的是白球;
(4) 从中一次性取出两球,取出的两球颜色不同.

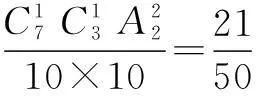





(本题也可以用(2)中的排列来解决,有殊途同归之效)
评注本题涉及到主要是概率计算中的顺序问题,正确理解有无顺序,合理运用排列组合乃至两个基本计数原理是解决问题的关键.
二、互斥、对立与独立混淆
为了对“互斥”、“对立”与“独立”这三者关系有个清晰的认识,特设计了下面的例子.
例2抛掷一颗骰子,记A为事件“落地向上的数为奇数”,B为事件“落地向上的数为偶数”,C为事件“落地向上的数为3的倍数”,D为事件“落地向上的数为大于3的数”,E为事件“落地向上的数为7”.判断下列每对事件的关系:
(1)A与B;(2)A与C;(3)B与C;
(4)A与D;(5)A与E.
解显然A={1,3,5},B={2,4,6},C={3,6},D={4,5,6},E={7}.
注意基本事件总数为6,可得
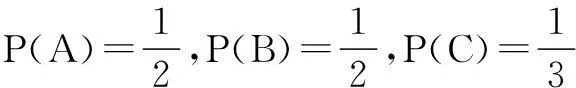
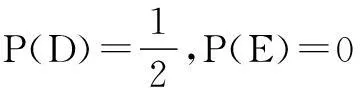
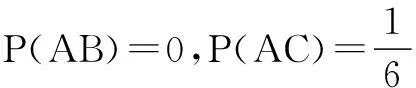

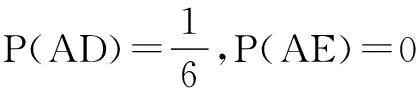
由互斥、对立及独立事件的概念,得结论如下:
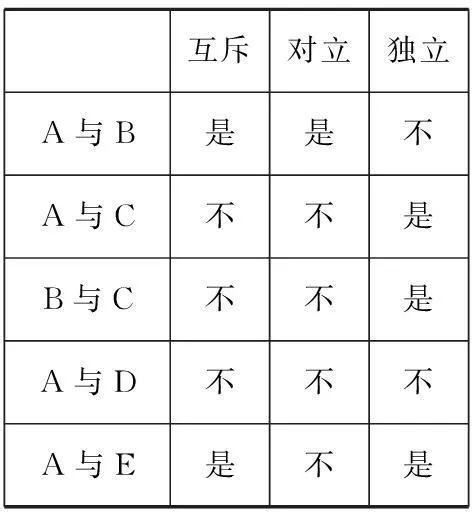
互斥对立独立A与B是是不A与C不不是B与C不不是A与D不不不A与E是不是
实际上,设若两个随机事件A、B相互独立,则说明这两个事件可以同时发生(因为两个事件的发生互不影响),而互斥的两个事件却不能同时发生(亦即一个事件发生了,另个事件就绝对不可能发生),故两个相互独立的事件通常不可能互斥.
反之,设若两个事件互斥,则一个事件的出现必导致另一个事件的不出现,这说明后者出现的概率受到了前者是否出现的影响,从而意味着这两个事件并不相互独立.
当然这只是一般情况,当有概率为零的事件时例外.
三、超几何分布与二项分布的区别
例3某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本算出他们的重量(单位:克).重量的分组区间为(490,495],(495,500],…(510,515],
由此得到样本的频率分布直方图,如图1所示.
(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列;
(3)从流水线上任取5件产品,求恰有2件产品合格的重量超过505克的概率.

解(1)重量超过505克的产品数量是:40×(0.05×5+0.01×5)=40×0.3=12.
(2)Y的分布列为:

Y012PC228C240C128·C112C240C212C240
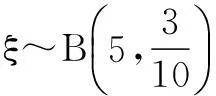
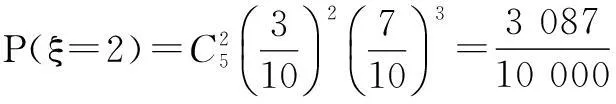
评注本题第三小题易犯的错误是利用超几何分布来解决.
超几何分布和二项分布的区别:
(1)本质区别:二项分布是独立重复试验,每一次发生的概率都一样,而超几何分布则会改变.如常见两种模型:有放回和无放回抽取.(有放回抽样时,每次抽取时的总体没有改变,因而每次抽到某物的概率都是相同的,可以看成是独立重复试验,此种抽样是二项分布模型.而不放回抽样时,当总体容量比较小时,从中取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模型)
(2)在统计中的区别:
①超几何分布需要知道总体的容量,而二项分布不需要;
②当总体的容量非常大时,采用二项分布;(当总体样本非常大时,虽说取出一个少一个,但对于总体的影响小之又小,故可以看做对概率没有影响,所以采用二项分布)
③如果用样本的频率估计为总体的概率,一般采用二项分布.
例4某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图2所示.
(1)估计这次测试数学成绩的平均分、中位数和众数;
(2)假设在[90,100]段的学生的数学成绩都不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任意抽取2个数,有放回地抽取了3次,记这3次抽取中,恰好是两个学生的数学成绩的次数为ξ,求ξ的分布列及数学期望Eξ.
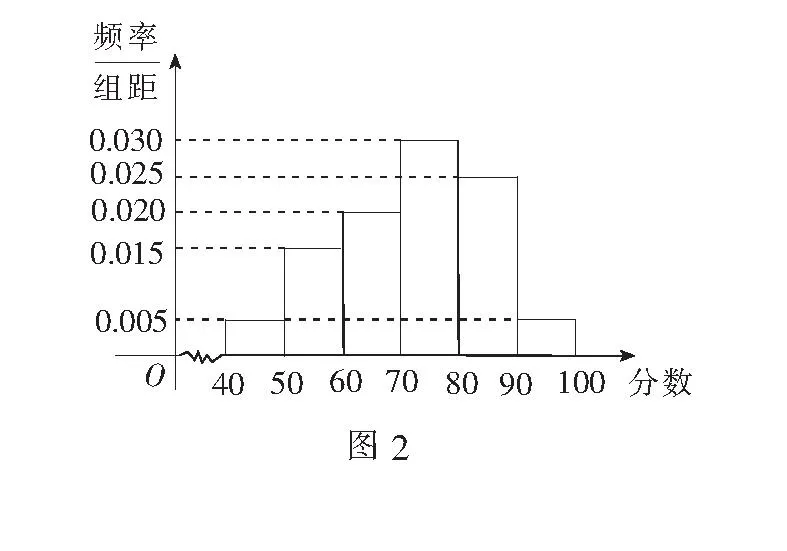
解(1)利用中值估算抽样学生的平均分:
45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05=72.
所以,估计这次考试的平均分是72分.

学生的成绩在[90,100]段的人数是0.005×10×80=4(人).

四、两种不同的条件概率
例5一个盒子中有大小形状相同的10个球,其中有6白球,4个黑球,
(1) 从盒子中任取两个球,已知第一次取到的球为黑球,求第二次取到的球也是黑球的概率;
(2) 从盒子中任取两个球,已知其中一个球为黑球,求另一个球也是黑球的概率.
解(1)已知第一次取到的球为黑球,故盒子中还剩下9个球,其中6白球,3个黑球,从中再任取一球为黑球的概率
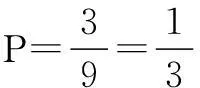

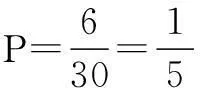
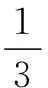
五.忽略基本事件的等可能性出错
例6把圆周4等分,A是其中一个分点,动点P在四个分点上按逆时针方向前进.投掷一个质地均匀的正四面体,它的四个面上分别写着1,2,3,4四个数字,P从点A出发,按照正四面体底面上所投掷的点数前进(数字为n就前进n个分点),转一周之前继续投掷.
(1)求点P恰好返回到点A的概率:
(2)在点P转一周能返回点A的所有结果中,用随机变量ξ表示点P返回A点时的投掷次数,求ξ的分布列和期望.
(2)错解:在恰能返回点A的情况下,ξ有1,2,3,4共四种取值的可能结果,且由(1)知

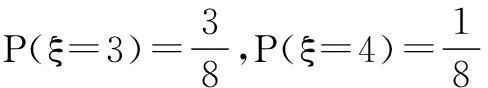
故ξ的分布列为

ξ1234P18383818


评注本例第(2)问的解法在很多教材和资料上比较常见,许多中学老师也对这一结果持相同的意见.究其原因,乃是对古典概型中基本事件的等可能没有正确地把握:在点P转一周能返回点A的所有结果认为是8种,且每一种都是等可能的.事实上,它们显然不是等可能的,应按照条件概率计算,ξ的分布列的正确结果如下:

ξ1234P6412548125121251125
