在“猜想、验证、证明”中获得——以“函数的和、差、积、商的导数”教学片段为例

汤爱民

(江苏省盐城师范学院第一附属中学，224002)



在“猜想、验证、证明”中获得
——以“函数的和、差、积、商的导数”教学片段为例

汤爱民

(江苏省盐城师范学院第一附属中学，224002)

日前,笔者有幸代表学校参加盐城市市区学校优质课比赛.比赛采取微课的形式,指定教学内容为“函数的和、差、积、商的导数”的一个片段,时间不超过15分钟．苏教版“函数的和、差、积、商的导数”教材内容只给出了一个引例及函数和、差、积、商的求导法则和两个例题．分析教材后,笔者认为这节课的重点是函数和、差、积、商的求导法则的运用,难点是函数的积的求导法则的推导,因此决定选择“函数的积的求导法则”这一片段参赛．现将教学设计整理如下，以供参考.

一、类比猜想,启发思考

我们刚才通过猜想并用导数的定义法验证了:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即

[f(x)±g(x)]′=f′(x)±g′(x).

那么,问: [f(x)g(x)]′与f′(x)和g′(x)有什么样的关系呢?

学生猜想后,继续问:

[f(x)g(x)]′=f′(x)g′(x)

是否正确?

设计意图此设计意在充分暴露学生的思维.受函数和(差)求导法则的影响,学生很容易猜想得出[f(x)g(x)]′=f′(x)g′(x)．引导学生运用x·x2这个反例来说明上面的猜想“[f(x)g(x)]′=f′(x)g′(x)”是错误的,防止知识负迁移．

问:刚才同学们猜想[f(x)g(x)]′与f′(x)和g′(x)的关系为[f(x)g(x)]′=f′(x)g′(x)．事实上,我们通过x·x2验证出[f(x)g(x)]′=f′(x)g′(x)这一猜想是错误的．那么,[f(x)g(x)]′与f′(x)和g′(x)究竟是什么样的关系呢?

二、问题探究,引出猜想

以函数f(x)=x和g(x)=x2为例,请同学们观察:

xx2

12x

与

3x2([f(x)g(x)]′)

之间的关系．

学生从“系数”和“项”两个方面很容易观察出上面的样式与“十字相乘法”十分相似,所以可以得出下面的关系式:

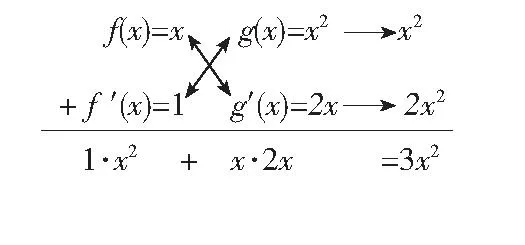
从而猜想出:

f′(x)g(x) +f(x)g′(x)

=[f(x)g(x)]′ .

①

三、实例检验,巩固猜想

现在,我们观察下表第2、第3列,看看是否满足①式结论．

例1请同学们填写下表：

f(x)g(x)x3x4x4函数f(x)=x,g(x)=x2f(x)=x2,g(x)=x2f(x)=x3,g(x)=x导数f(x)=1,g'(x)=2x[f(x)g(x)]'3x2

解填表如下：

f(x)g(x)x3x4x4函数f(x)=x,g(x)=x2f(x)=x2,g(x)=x2f(x)=x3,g(x)=x导数f'(x)=1g'(x)=2xf'(x)=2xg'(x)=2xf'(x)=3x2,g'(x)=1[f(x)·g(x)]'3x24x34x3

那么,[f(x)g(x)]′与f′(x)和g′(x)的关系是否就是[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)?

设计意图通过拆分x4为两函数积的形式,验证上面的猜想,让学生在特例检验的过程中对函数积的求导法则的结构有更深入的了解．

四、证明猜想,得出结论

对一般情形的猜想,同样需要严格的证明来验证它的正确性．

证明设y=f(x)g(x)，则

-f(x)g(x+Δx)

+f(x)g(x+Δx)-f(x)g(x) ].

②

的形式,以便使证明过程方便进行下去.

于是，

+f(x)[g(x+Δx)-g(x)]}

当Δx→0时,由上式可得

[f(x)g(x)]′=f′(x)g(x)

+f(x)g′(x)．

因此,我们有函数积的求导法则:

[f(x)g(x)]′=f′(x)g(x)

+f(x)g′(x).

特别地,当函数g(x)=C,C为常数时,有

[Cf(x)]′=Cf′(x)．

设计意图将Cf(x)的求导法则调整到函数积的求导法则后面讲解,学生更容易理解．

五、当堂检测,巩固概念

例2求下列函数的导数:

(1) f(x)=xsin x;

(2) f(x)=(2x2+3)(3x-2)．

设计意图第(2)问没有照搬课本题目,主要考虑到:一是帮助学生运用函数积的求导法则;二是对原函数进行整理,运用函数和的求导法则解决问题,培养学生转化的思想,帮助学生树立整体观念．

六、回顾反思,总结提升

通过“猜想、验证、证明”,学生收获的不仅是“函数的积的求导法则”,更重要的是收获了发现“函数的积的求导法则”的方法：

(1)由合情猜想引出疑问,提出对猜想结果的质疑．

(2)通过f(x)=x、g(x)=x2和它们的导数f′(x)=1、g′(x)=2x,引导学生联想到“十字相乘法”,发现1·x2+x·2x=3x2,从而重新猜想出

[f(x)g(x)]′=f′(x)g(x)

+f(x)g′(x).

(3)教会学生发现规律(本质)的一般方法:

引出疑问——探究猜想——检验证明