运用整体思想巧解数学题

龚　勤

(湖南省岳阳市第一中学，414000)



○解题研究○

运用整体思想巧解数学题

龚勤

(湖南省岳阳市第一中学，414000)

有很多数学问题,如果我们有意识地放大考察问题的“视角”,往往能发现问题中隐含的某个“整体”,利用这个“整体”对问题实施调节与转化,常常能使问题快速获解.一般地,我们把这种从整体观点出发,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题思想方法,称为整体思想方法.它是通过研究问题的整体形式、整体结构,并对其进行调节和转化使问题获解的一种方法.运用整体思想,可以理清数学学习中的思维障碍,可以使繁难的问题得到巧妙的解决．它是数学解题中一个极其重要而有效的策略,是提高解题速度的有效途径．

一、整体补形

(A)40(B)80

(C)160(D)240

分析若按常规方法利用体积公式求解,底面积可用海伦公式求出,但顶点到底面的高无法作出,自然无法求出．若能换个角度来思考,注意到三棱锥的有三对边两两相等,若能把它放在一个特定的长方体中,则问题不难解决．

解析把三棱锥P——ABC补成一个长方体AEBG——FPDC,易知三棱锥P——ABC的各边分别是长方体的面对角线．不妨令PE=x,EB=y,EA=z,则由已知，有

解得x=6,y=8,z=10.从而知

VP-ABC=VAEBG-FPDC-VP-AEB-VC-ABG

-VB-PDC-VA-FPC

=VAEBG-FPDC-4VP-AEB

=160.

二、整体补式

例2求sin220°+cos250°+sin20°cos50°的值．

解令A=sin220°+cos250°+sin20°cos50°,B=cos220°+sin250°+cos20° ·sin50°，则

A+B=2+sin70°,

①

②

三、整体构形

例3已知 x,y,z∈(0,1),求证:

x(1-y)+y(1-z)+z(1-x)<1.

分析观察到x+(1-x)=y+(1-y)=z+(1-z)=1及乘积式,联想到用面积公式．

四、整体代换

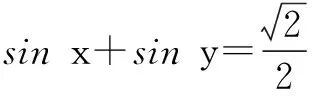
解设u=cosx+cosy,将已知式与待求式两边平方得

①

u2=cos2x+2cosxcosy+cos2y．

②

①+②，得

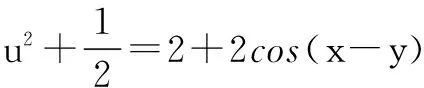
因为-2≤2cos(x-y)≤2,

点评利用整体代换构建不等式也是求解此类问题的最基本的方法．

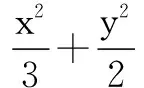
分析按照常规思路,只需求出直线P1P2的斜率k,待定系数法写出直线P1P2的点斜式方程与椭圆方程联立消元后得一元二次方程,其两根为P1,P2两点横坐标,利用中点坐标公式及韦达定理可得关于k的方程,但运算量较大．

解设P1(x1,y1),P2(x2,y2)，则

两式相减得

=0.

又P为P1P2中点,

∴x1+x2=2,y1+y2=2，

当x1=x2时,直线不满足条件,故所求的直线为2x+3y-5=0．

我们观察与思考数学问题时,着眼结构的整体性,可以简化解题思路，有利于确定解题的突破口或者总体思路.在教学中,我们应积极引导学生全面考虑问题,养成整体分析的思维习惯,培养良好的思维品质,以优化其数学素质．

五、整体联想

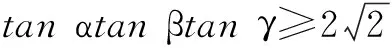
分析由题设条件,易联想到长方体对角线的性质:长方体的一条对角线与同一个顶点上的三条棱所成的角的余弦的平方和等于1,于是构造长方体解题．

证明如图2,设以a,b,c为长,宽,高的长方体ABCD-A1B1C1D1的对角线AC1与过点A的三条棱AD,AB,AA1所成的角分别为α,β,γ.则

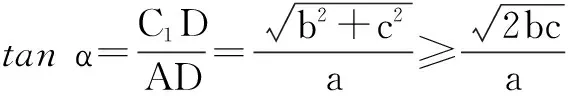
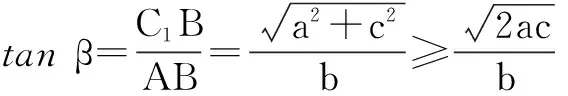
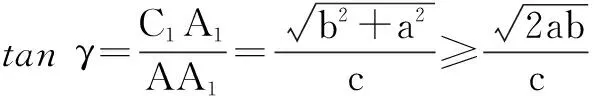
点评数学解题,由于题目中的特殊的结构形式,有时应充分发挥类比、联想,合理构造,从而起到简捷理想的解题效果．

思路整体联想→发现原型→猜想论证.

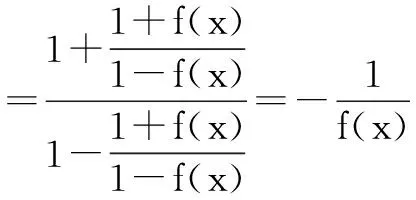
故f (x)是周期函数,且4a是它的一个周期.

解∵2a2=5-3a,2b2=5-3b且a≠b,所以a与b是方程2x2+3x-5=0的两不相等实根,

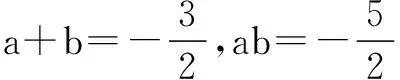
代入化简后求得

评注本题求解关键是如何把握条件及结论的整体结构,构造一元二次方程及利用根与系数的关系.

纵上所述,数学教学不能满足于单纯的知识灌输、就题论题.应在知识与能力之间架设一座桥梁,使学生掌握数学中最本质的东西——数学思想,尤其是整体思想,才会有利于学生清除思维障碍,理解数学知识,有利于巧妙解决数学问题,发展创造性思维能力．