对一道试题的探究

张巨洪　蒋　英

(广东省茂名市电白区第一中学，525400)



对一道试题的探究

张巨洪蒋英

(广东省茂名市电白区第一中学，525400)

原题(广东省2016年适应性测试理科第20题)已知抛物线C:y2=4x,过其焦点F作两条相互垂直且不平行于x轴的直线,分别交抛物线C于点P1,P2和点P3,P4,线段P1P2,P3P4的中点分别记为M1,M2.

(1)求∆FM1M2面积的最小值;

(2)求线段M1M2的中点P满足的方程.

解(1)设P1(x1,y1),P2(x2,y2),

直线P1P2∶x=my+1(m≠0).

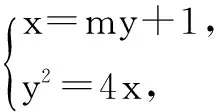
可得y2-4my-4=0.

于是x1+x2=4m2+2,

x1x2=8m2+1,

y1+y2=4m,

y1y2=-4.

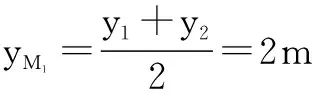
xM1=m·yM1+1

=2m2+1,

可知点M1(2m2+1,2m)；

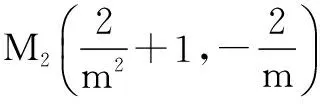
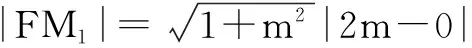
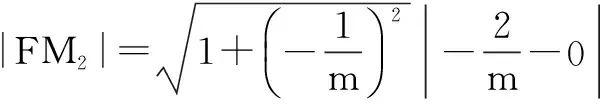
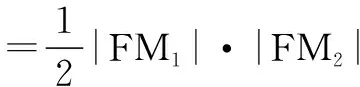
≥4,

当且仅当m=±1时等号成立．

故∆FM1M2面积的最小值为4.

(2)设点P(x,y),因为点P为线段M1M2的中点,所以

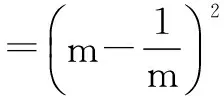
=x-3.

故线段M1M2的中点P满足的方程为x=y2+3.

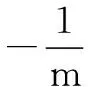
引申1求证:直线M1M2恒过定点(3,0).

证明当直线M1M2的斜率不存在时,有

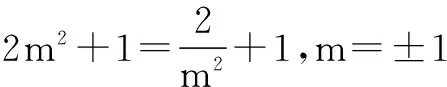
所以M1(3,2),M2(3,-2)或M1(3,-2),M2(3,2),则直线M1M2的方程为x=3.

当直线M1M2的斜率存在时,则直线M1M2的斜率

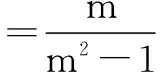
其方程为

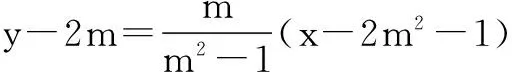
即mx+(1-m2)y-3m=0.

显然,不论m为何值,(3,0)均满足上述方程.

综上可知,直线M1M2恒过定点(3,0)

结论1在抛物线中,过焦点且互相垂直的两条弦的中点连线必过定点.

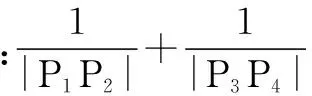
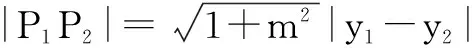
=4(m2+1)，

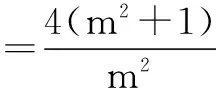
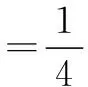
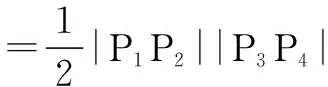
≥32,

当且仅当m=±1时等号成立．

结论2在抛物线中,过焦点且互相垂直的两条弦的倒数和为定值．

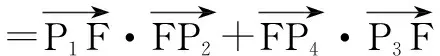
=(1-x1,-y1)·(x2-1,y2)

=(1-x1)(x2-1)-y1y2

=x1+x2-x1x2-1-y1y2

=-4(m2+1)，

同理可得

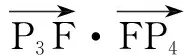
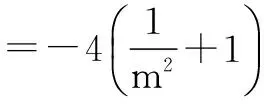
≥64,

当且仅当m=±1时等号成立．

以上几类题型对椭圆,双曲线都有类似的结论,读者朋友们不妨一试．

反思很多学生都觉得解析几何题难度大,尤其是计算量很大.因此，教师在平时的教学中,要优化解题方法．解析几何中的一些基本问题,如本文中的两直线垂直问题,我们只需要设其中一条直线,另一条直线把斜率换成负倒数就可以了；又如求两点距离时用弦长公式比用两点距离公式要简单得多；再如本文中过点(1,0)的直线设为x=my+1比设为y=k(x-1)要好,大大简化了运算量．因此,在高三的解题教学中一定要注意解题后的总结和反思,要做到一题多解,多解归一,一题多变．我们的老师不但自己要善于总结与反思,更要教会学生总结与反思．