解三角形问题的思路探析与教学
2016-08-31房得阳
李 凯 房得阳
(西北师范大学教育学院,730070)
解三角形问题的思路探析与教学
李凯房得阳
(西北师范大学教育学院,730070)
解三角形一直以来是全国各地高考考查的热点题型之一.本板块知识以三角形为载体,涵盖求三角形的边、角、面积、三角函数值以及综合运用相关知识解决实际问题的具体题目,重点是如何运用正弦定理和余弦定理解三角形问题.本文针对这一热点题型,概述几种常见解三角形的思路,并给出几点教学建议,旨在促进教学,供大家交流学习.
一、本题型重、难点分析
重点:正弦定理和余弦定理及其应用.
难点:(1)灵活运用正弦定理、余弦定理及其变形形式解题;
(2)将有关实际应用问题抽象为解三角形以及相关实际问题.
二、正、余弦定理知识点剖析
1.正弦、余弦定理及其变形公式
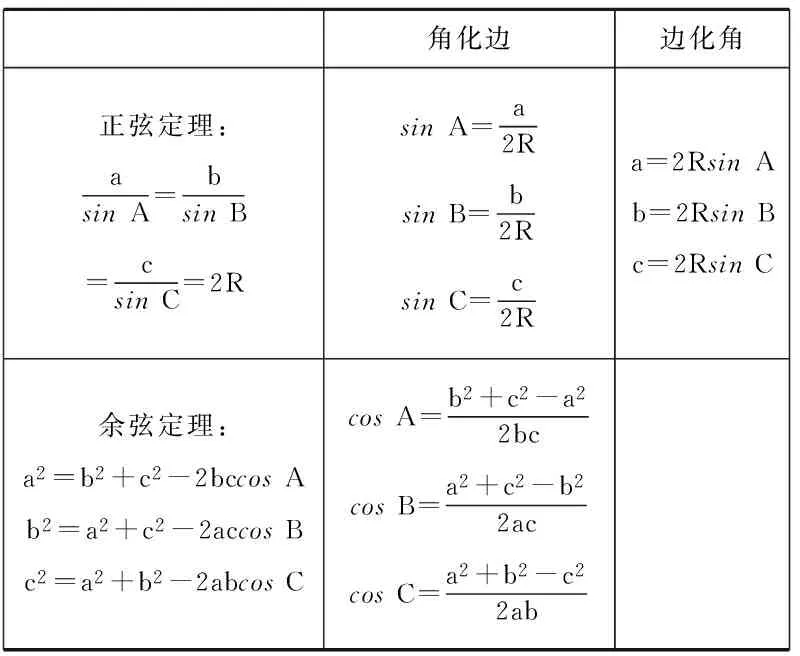
角化边边化角正弦定理:asinA=bsinB=csinC=2RsinA=a2RsinB=b2RsinC=c2Ra=2RsinAb=2RsinBc=2RsinC余弦定理:a2=b2+c2-2bccosAb2=a2+c2-2accosBc2=a2+b2-2abcosCcosA=b2+c2-a22bccosB=a2+c2-b22accosC=a2+b2-c22ab
说明:表中a,b,c分别是∆ABC的三个角A、B、C所对的边,R是∆ABC的外接圆半径.
“角化边”是指将一个角的三角函数(如sinA,cosA…)转化成对应边的形式;
“边化角”是指将三角形某一边转化三角函数值的形式.
2.三角形面积公式及其变形
设∆ABC的面积为S,内切圆半径为r,则有下列公式及其变形:
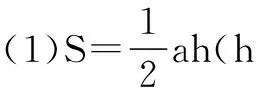
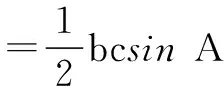

边化角:

角化边:

说明:当三角形面积确定时,边的乘积形式也可以转化成角的三角函数值的形式.

三、两种解题思路的概述
1.思路“角化边”
这种思路在于当题目已知某些对应边时,我们得顺理成章地想到“角化边”的正余弦的两种形式.

解依正弦定理,得

依余弦定理,得

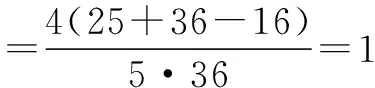

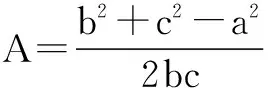

化简得b2-6b+8=0,解得b=2或4.
因为b 因为该三角形为锐角三角形,所以 由余弦定理 a2=b2+c2-2bccosA代入,得a=7. 解(1) 由三角形面积公式,得 由S∆ABD=2S∆ADC,∠BAD=∠CAD,得 AB=2AC. 由正弦定理,得 2.思路“边化角” “边化角”解题思路在于当题目已知某个角度或是某个角的函数值时,需要想到“边化角”的正余弦定理的变形形式. (1)求A; 解(1)因为m平行n,所以 由正弦定理(边化角),得 (2)由余弦定理a2=b2+c2-2bccosA,代入已知数值,得 c2-2c-3=0,解得c=3或-1(舍). 依三角形面积公式,得 已知b-c=2,所以b=6,c=4. 由余弦定理a2=b2+c2-2bccosA,代入数值,得a=8. 3、两种思路的综合应用 如果题目给出的式子中既有边又有角,则两种思路都可以作为一种解题切入点. 例7若b=asinC,c=acosB,判断∆ABC的形状. 解法1(边化角)依正弦定理,得 2RsinB=2RsinAsinC, ① 2RsinC=2RsinAcosB. ② 由②得sin[π-(A+B)]=sinAsinB, 整理,得cosAsinB=0, 代入①式,得sinB=sinC,B=C, 因此,∆ABC为等腰直角三角形. 解法2 (角化边)由余弦定理,得 又由b=asinC,得sinB=sinAsinC=sinC,所以B=C. 故∆ABC为等腰直角三角形. (1)重视培养学生常规思维的教学及练习,掌握通式通法.“边化角”由边求角,“角化边”由角求边,通过题目已知量找到未知量的表示形式,至于用正弦定理还是余弦定理,应由题目而定.涉及sinA(sinB或是sinC)首先联想到正弦定理,涉及cosA(cosB或是cosC)联想到余弦定理.当然这也不是绝对的,但是至少是有助于思维的一种定式,对于当前的应试高考还是有很大辅助作用. (2)正确理解正、余定理的内涵,快速选择运用定理.有些题目比如例7,两种思路都能走得通,不妨在教学中让学生动手多加练习,拓展思维辨析.然而这种题目局限于有角有边,并且利用边化角时式子两边都得有边的存在,不然会引入未知量R,又会干扰做题.在教学中教师必须强调面临此种题目的解题思路,避免运用定理混乱,盲目做题. (3)反复训练正、余弦定理的几种变形,让形式牢记于心.在教学过程中,让学生自己动手对正、余弦定理进行变形,这样不仅有利于识记,也助于他们清晰地理解这一知识点.让学生亲历数学知识发现的过程,有助于学生对于该知识点的理解与掌握. 有关三角形的常考题型的解题落脚点往往会采用这两种思路.不论是“角化边”,还是“边化角”我们都需要熟练掌握正、余弦定理及其变形,运用它们进行转化,简化过程.当然也要灵活变通,当其中一种思路行不通时,及时转变思路也是至关重要的.相信在教师的指引下这两种思路会让学生对解三角形常见的题型有一个清晰的解题思路与方法.





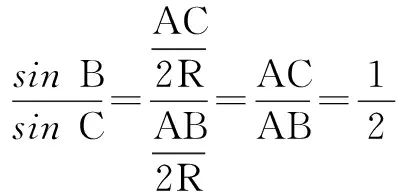




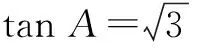
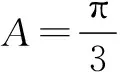


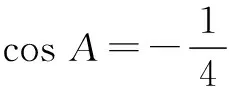
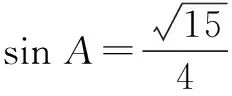



四、教学建议
