超级画板支持下椭圆外切平行四边形面积最值问题的探究和思考
2016-08-31邓城
邓 城
(广东省广州市增城区增城中学,511300)
○数学探究○
超级画板支持下椭圆外切平行四边形面积最值问题的探究和思考
邓城
(广东省广州市增城区增城中学,511300)
圆锥曲线中涉及的面积问题由于图形变化多样,曲线和直线的方程复杂,造成面积难以测量或计算,导致研究面积最值主要靠画图猜想,再加以严格证明,这样使得研究的难度增大.而在超级画板的支持下,面积的大小可以精准测量,且能够随着图形的变化动态显示面积的数值,方便确定面积最值大小,发现取到最值时图形的几何特征,进而得到新的数学猜想,并且在超级画板的帮助下容易寻找到证明的突破口.笔者借助超级画板,对椭圆外切平行四边形的面积最值问题进行了研究探索,得到了若干性质结论,也对超级画板支持下的解析几何教学有了初步的认识与思考.
一、超级画板支持下的探究发现
椭圆的外切平行四边形是指四条边均与椭圆相切的平行四边形.显然,一个确定的椭圆有无数个外切平行四边形,且存在面积最
(1)真自主、真合作.知识可以传承,但能力只有通过真真切切的亲身体验和感悟才能生成.教学中应尽可能地让学生有更多的时间去自主探究,给学生机会交流,去展示最原始的、最火热的思维过程.
(2)在问题设计过程中求真.在设计探究问题时要考虑问题的解决是否具有多角度、多方向性,考查学生的思维方法是否具有多样性,反映学生的思维品质是否具有多层次性.案例中的前三个问题,可以锻炼了学生全面的、多角度的研究问题能力,特别是对问题1的三名同学不同视角的解释,充分地展现了学生思维的灵活与机智;问题4中所得到的多个优美不等式的探究成果,正是全体同学的积极参与,通过自主合作的集体智慧结晶;问题4、问题5的解决,有效地对“特殊与一般”、“有限与无限”、“化归与转化”的数学思想方法进行了渗透.
3.高三数学复习的探究性教学中应充分挖掘数学之“美”
数学的美包括统一、和谐、简洁、对称、奇异、逻辑、严谨等方面.我们教师应在教学中充分挖掘数学之美,以美启真,调动学生的学习热情,积极地参与思考,在探究中去感知、欣赏、应用和创造美.这样做不仅让学生陶冶了情操,还激发了学生学习数学的兴趣,培养了数学思维能力,促进"德"、"智"的协调发展.学生在问题1的解决中体验了数形结合的和谐统一之美、数学问题解决的类比和简洁之美;学生在问题4的探究中生成了一组优美的不等式,赏析了数学的对称美;学生在问题4(2)及问题5的解决中领略了数学的逻辑和应用之美;用诗歌和对联对数学思想和方法加以总结,赋给了它们美的表现形式,使学生更乐于接受,同时也升华了数学思想.从教学反馈来看,效果很好.
小的外切平行四边形,但最小值是多少以及何时取到最小值却是值得思考的问题.然而由于椭圆的切线方程本身就难以处理,再加上涉及到的切线有四条,这使得平常教学和考试中基本不会出现与椭圆外切平行四边形有关的问题.但在超级画板的支持下,我们可以很方便地对其进行深入地研究,并能发现隐藏其中的有趣性质.

探究1当A、B两点为椭圆的上下顶点,即有切线EF和GH平行于x轴时,在椭圆上移动切点C、D,由超级画板的测量功能容易发现当切线EG和FH平行于y轴时有外切平行四边形的面积最小值为4ab=24,此时外切平行四边形是个特殊的矩形.
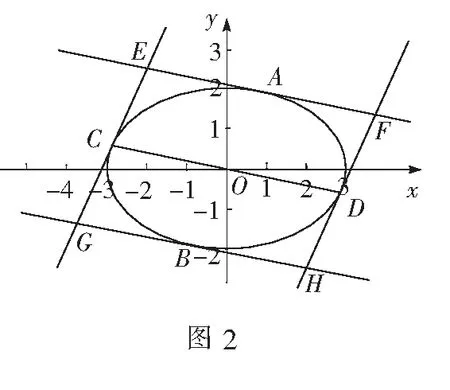
探究2当过A、B两点的切线EF和GH不平行于x轴时,外切平行四边形的面积的最小值还是一样吗?借助超级画板,笔者惊讶地发现当移动切点C、D到某个位置时面积有一样的最小值24;并且通过取最值时的图形特征容易猜测有CD∥EF,利用超级画板的测量功能果真发现kCD=kEF(如图2所示).
探究3改变椭圆的大小和切线的位置,借助超级画板的动态测量功能发现椭圆外切平行四边形面积的最小值仍然为4ab,且取到最值时的几何特征仍然为CD∥EF.
有趣的是,若此猜想成立则容易发现面积取到最小值的外切平行四边形有无数个,其中包括“探究1”中的特殊矩形.
二、猜想的证明
在超级画板的支持下容易发现外切平行四边形切点的位置变化导致了面积的变化,因此外切四边形面积的表达可以考虑通过切点的坐标来表示,由外切平行四边形的几何特征只需设两个切点即可.下面是猜想的证明:
设A(x1,y1)、C(x2,y2),则有B(-x1,-y1),D(-x2,-y2),易得椭圆的四条切线方程:
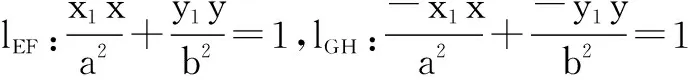
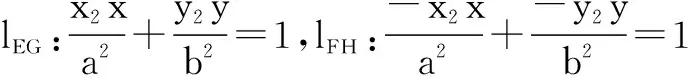
由平行直线的距离公式,易得切线EF与切线GH间的距离
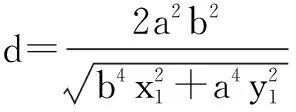
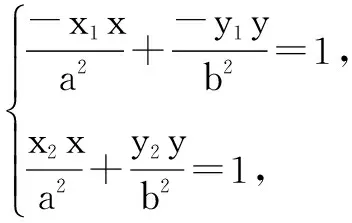




所以,平行四边形EGHF的面积
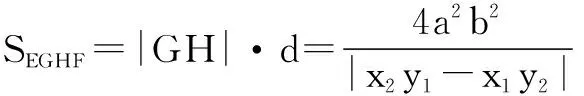


≥4ab,

故有kCD=kGH,即CD∥EF时外切平行四边形的面积取到最小值4ab.
三、反思
(1) 超级画板支持下的解析几何探究能丰富学生的学习方式,提升学习效果.新课标提出:“高中数学课程应提倡利用信息技术来呈现以往教学中难以呈现的课程内容,在保证笔算训练的前提下,尽可能使用科学型计算器、各种数学教育技术平台,加强数学教学与信息技术的结合,鼓励学生运用计算机、计算器等进行探索和发现.”超级画板便是符合教育发展需要的信息技术软件,它具备的强大交互性使得学生能在“做中学”和“玩中学”,丰富了学生的学习方式.例如,在前面所提的外切平行四边形面积的最值问题中,超级画板给予了传统教学中不能提供的“数学实验场”,学生稍经培训便可以自主地根据研究目标有针对性地修改数据、变动参数、移动或跟踪几何对象来观察目标对象的变化情况,进而能直观地获得数学猜想.可见,解析几何教学中应用超级画板进行探究有助于学生体验探究的过程,感受发现新规律的乐趣;同时,也能帮助学生养成自主研究的学习方式,提升学习效果.
(2)超级画板支持下的解析几何探究能开拓学生的视野,加强数学文化的传播.基于解析几何特别是圆锥曲线的学习难度,新课标对解析几何的学习要求比以往有一定程度的降低.这从减少学生的学习负担的角度来看是合适的,但从教学实践看许多教师却也因此减少了向学生传递解析几何中丰富多彩的数学美的机会,结果造成虽然学习难度降低了,但是大部分学生对解析几何特别是圆锥曲线仍然感到枯燥无味,学习积极性较低.如今,在超级画板的支持下,教师可以非常方便直观地展示解析几何中的众多优美性质,开拓学生的数学视野并让学生感受蕴含其中的数学文化.例如,在前面所提外切四边形面积的探讨中,正是因为有了超级画板的支持,才能让人直观感受到面积取到最值时表现出的奇异性质,否则只能遗憾错失一次数学美的发现经历.值得注意的是,超级画板软件的使用非常简单方便,对信息化时代的学生来说更不存在增加负担问题,相反恰恰是学习减负的工具.(本文系广州市教育科学“十二五”规划2015年度课题——“超级画板支持下高中数学解析几何教学的研究”(课题编号:1201553470)的阶段性研究成果之一)
