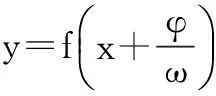函数y=Asin(ωx+φ)的图象的教学案例

徐惠杰

(江苏省常州高级中学，213003)



函数y=Asin(ωx+φ)的图象的教学案例

徐惠杰

(江苏省常州高级中学，213003)

一、学情分析

本节课的授课对象是四星级重点高中重点班学生,基础较好,思维较活跃,有一定的观察、分析能力及合作学习的基础.从已有的知识看学生已经在初中从点的对应关系研究过二次函数的图象变换,在高中指数对数学习中知道了函数y=f(x)和函数y=f(x+a)图象之间的关系.

二、 教材分析

所用教材为《普通高中课程标准实验教科书·数学(必修4)》(苏教版).函数y=Asin(ωx+φ)的图象是第1章“三角函数”中第3节的内容.课本是按照先作图观察再得出一般结论来呈现，这样看上去比较“顺其自然”,但笔者认为学生的思维并没有深入,由此笔者从图象上点的对应关系进行如下教学设计.

三、教学目标

(1)能由正弦曲线通过平移、伸缩变换得到y=Asin(ωx+φ)的图象,并在这个过程中认识其与函数y=Asin(ωx+φ)的联系.

(2)通过正弦函数到函数y=Asin(ωx+φ)图象的变换让学生体会由简单到复杂、由特殊到一般的过程,培养学生分析问题和解决问题的能力.

四、教学重点和难点

教学重点函数y=sinx与函数y=Asin(ωx+φ)的图象变换.

教学难点函数y=sinωx与函数y=sinx的关系,函数y=sin(ωx+φ)与y=sinωx图象之间的关系.

五、教学过程

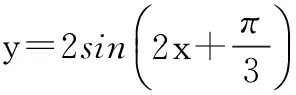
生:描点法，图象的变换，用几何画板.

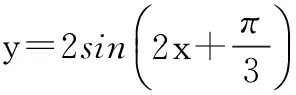
生:几何画板, 图象变换.(追问：你怎么想到通过图象变换的呢?感觉和y=sinx的图象有关系)

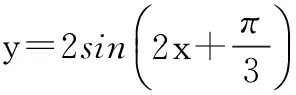
生:不行!平移变换不能改变x前的系数.

师:很好,说明平移变换只能改变φ的值,那除了平移变换我们还要研究y=sinx与哪个图象之间的关系呢?

生:研究函数y=sinx与y=2sinx,y=sin2x之间的关系.

一般地,函数y=sin(x+φ)的图象可以由函数y=sinx的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位长度而得到的.

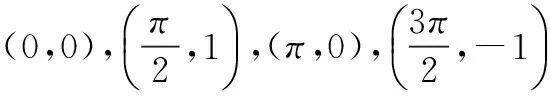
师:如果点A(x0,y0)在y=sinx图象上,则点B(x0,2y0)在函数y=2sinx的图象上；同样,若点B在函数y=2sinx的图象上,在y=sinx的图象上也能找到一个点与之对应.也就是说将y=sinx图象上所有点的横坐标不变,纵坐标变为原来的2倍就能得到函数y=2sinx的图象.(师生一起通过几何画板观察点的对应)

一般地,函数y=Asinx(A>0且A≠1)的图象,可以看做是将函数y=sinx的图象上所有点的纵坐标变为原来的A倍(纵坐标不变)而得到的.

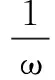
师:刚才我们通过点的对应关系研究了3种变换,现在有这样2个问题:

既然是天意，就不能违抗。他想，也许这对她来说是一件好事，是一件以后想起来不必矛盾和纠结的好事。还是原配好。她曾经说过。每次在一起面对他的为难甚至是显得虚妄的希望时，她总是这样泼冷水。显然，他们不再是狂躁的孩子。她不会因此离开家庭，虽然因为寂寞她接受了他的追求，并且全身心地享受着这份另类的激情。而他显出的虚妄多是在她矛盾愧疚的时候出现。我是好女人吗？会遭到唾弃吗？等高涨的潮水退去的时候，突兀的岩层理性地裸露出来。于是，在她无序的自责中，他会挺身而出，骑士般地说，不要等下辈子了，让我这辈子就娶你吧。我什么都可以舍得。

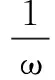
(2)y=sin2x的图象向右平移一个单位得到哪个函数的图象?

生3:得到y=sin(2x-1)的图象.

我们来验证此结论是否正确:假如结论正确，即点A(x0,y0)在函数y=sin2x的图象上，则B(x0+1,y0)在函数y=sin(2x-1)的图象上，因为y0=sin2x0，y=sin[2(x0+1)-1]=sin(2x0+1)≠y0，所以结论错误.

生4:y=sin(2x-2).

追问:你怎么证明你的结论是正确的?

方法1如果A(x0,y0)在函数y=sin2x的图象上，则B(x0+1,y0)在函数y=sin(2x-2)的图象上，因为y0=sin2x0，y=sin[2(x0+1)-2]=sin2x0=y0，所以结论正确.

方法2设f(x)=sin2x，则f(x-1)=sin2(x-1)=sin(2x-2).

师:一般地，函数y=sinωx(ω>0)如何得到函数y=sin(ωx+φ)的图象呢?

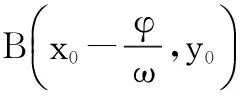
课堂小练:

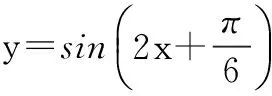
课堂小结(略)

六、 几点反思

1.关于引入

“如何画函数y=Asin(ωx+φ)的图象”是本节课要解决的核心问题.教材直接告知找与函数y=sinx的关系，即通过变换得到，但在备课时,笔者认为知识的产生有“来龙去脉”,先让学生尝试描点作图法画图象,在失败的情况下，再去尝试图象变换的方法,进而复习之前学过的平移知识的结论和研究方法,显得顺畅自然.

2.关于图象变换的研究方法

如果本节课图象的关系采用先几何画板作图再归纳规律也可以顺利完成教学任务，但本节课笔者始终立足于对变换本质的理解,即通过图象上对应点的关系理解两个图象之间的关系,虽然刚开始学生觉得有难度,但理解后学生就能从本质上掌握,对常见的图象变换的易错题也就理解了.

3.关于图象变换＂形式化＂的渗透