关于两个Diophantine方程的求解
2016-08-31许宏鑫赵西卿
许宏鑫,赵西卿
(延安大学 数学与计算机科学学院,陕西 延安 716000)
关于两个Diophantine方程的求解
许宏鑫,赵西卿
(延安大学 数学与计算机科学学院,陕西 延安716000)

不定方程;Euclid域;整数解
关于不定方程
x2+D=4yn
(1)
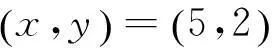
1 预备知识
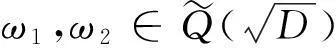
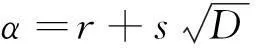
引理2设D满足引理1的条件[6],及
则α是二次代数整数的充要条件是它可表示为α=m+nω,m,n∈Z,n≠0。
(ⅰ) 当D=-2或D≤-5时,仅有±1;
(ⅱ) 当D=-1时,有±1,±i;
(ⅳ) 当D>1,D≡2,3(mod4)时,有
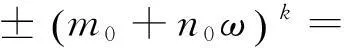
k=±1,±2,…
(ⅴ) 当D>1,D≡1(mod4)时,有
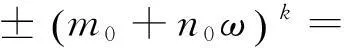
k=±1,±2,…
2 定理及其证明
定理1不定方程
x2+3=4y5,x,y∈Z
(2)
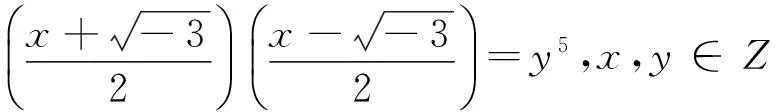
(3)
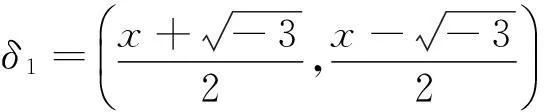
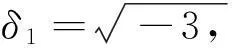
情形一,即
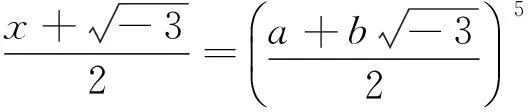
(4)
情形二,即
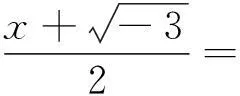
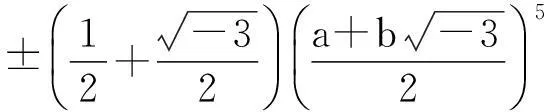
(5)
若式(4)成立,则有

化简得


比较两边的系数有
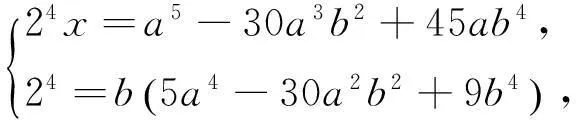
(6)
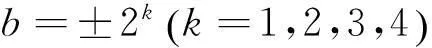
(2)若b=1,由方程组(6)的第二个等式有5a4-30a2-7=0,此时方程没有整数解。
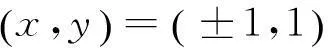
若式(5)成立,则有

化简得
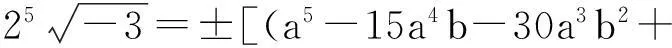
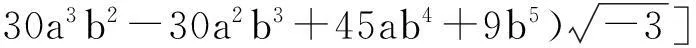
比较两边的系数有
(7)
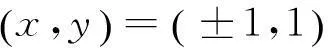
定理2不定方程
x2-3=4y5,x,y∈Z
(8)
无整数解。
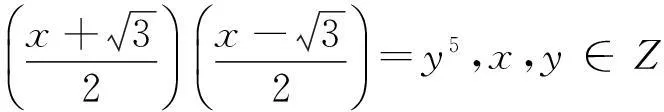
(9)
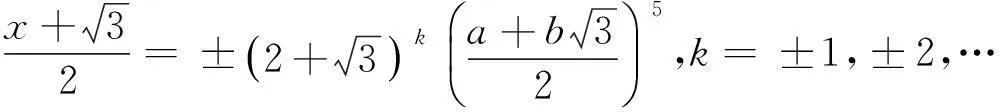
(10)
当k=1时,式(10)即为
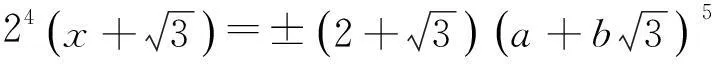
整理并比较两边的系数有
(11)
同理可证,当k取不等于1的其他整数时,这样的整数a,b仍是不存在的,因此不定方程(8)无整数解。
综上所述,不定方程x2-3=4y5,x,y∈Z无整数解。
3 结语
在不定方程x2+D=4yn的研究基础之上,利用二次Euclid域的整除理论讨论了不定方程x2±3=4y5,x,y∈Z的整数解情况,得出不定方程x2+3=4y5,x,y∈Z仅有整数解(x,y)=(±1,1),而不定方程x2-3=4y5,x,y∈Z无整数解。
现今,不定方程x2+D=4yn在虚二次Euclid域中的研究已经比较成熟,而在实二次Euclid域中仍有探究的空间。实二次域中共有16个Euclid域,因此我们可以在这16个Euclid域中进一步探索此不定方程的整数解。
[1]张丽平.关于不定方程x2+7=4y3[J].长春工程学院学报:自然科学版,2007,8(1):84-85.
[2]王振,李小燕.关于不定方程x2+11=4y3[J].重庆工商大学学报:自然科学版,2009,26(6):551-552.
[3]邬毅.关于不定方程x2+11=4y5的唯一正整数解[J].高师理科学刊,2006,26(2):7-8.
[4]邬毅,龙兰.Euclid域中Diophantus方程的整数解[J].数学杂志,2015,35(4):1 012-1 016.
[5]邬毅,杨懿,龙兰,等.关于二次域理论求解一类Diophantus方程的整数解[J].数学杂志,2015,35(5):1 197-1 200.
[6]潘承洞,潘承彪.代数数论[M].第3版.济南:山东大学出版社,2001.
[9]冯蕾,赵西卿,刘建,等.一个包含Smarandache对偶函数的方程的正整数解[J].甘肃科学学报,2015,27(6):1-4.
Solution of Two Diophantine Equations
Xu Hongxin,Zhao Xiqing
(College of Mathematics and Computer Science,Yan’an University,Yan’an 716000,China)
Indefinite equation;Euclid domain;Integer solution
10.16468/j.cnki.issn1004-0366.2016.04.003.
2016-01-19;
2016-03-18.
陕西省科技厅自然科学基金项目(2013JQ1019);延安大学自然科学专项基金项目(YDZ2013-05);延安大学研究生教育创新计划项目(张利霞).
许宏鑫(1989-),女,陕西靖边人,硕士研究生,研究方向为数论.E-mail:865747084@qq.com.
O156.7
A
1004-0366(2016)04-0009-04
引用格式:Xu Hongxin,Zhao Xiqing.Solution of Two Diophantine Equations[J].Journal of Gansu Sciences,2016,28(4):9-12.[许宏鑫,赵西卿.关于两个Diophantine方程的求解[J].甘肃科学学报,2016,28(4):9-12.]
