平面上一类特殊齐次Moran集的Packing维数下界
2016-08-31胡晓梅
胡晓梅
(1.湖北科技学院 数学与统计学院,湖北 咸宁 437100;2.华中师范大学 数学与统计学学院,湖北 武汉 430079)
平面上一类特殊齐次Moran集的Packing维数下界
胡晓梅1,2
(1.湖北科技学院 数学与统计学院,湖北 咸宁437100;2.华中师范大学 数学与统计学学院,湖北 武汉430079)
研究构造了平面上一类特殊的齐次Moran集,通过分析其结构并利用分形几何中计算维数的方法和技巧,证明得到了它们的Packing维数下界。
齐次Moran集;Packing维数;下界
1 预备知识
Moran集是一类不具有自相似结构的分形集,它与数学其他分支的联系非常密切。例如,在动力系统方面[1,2]、度量数论方面[3,4]、Lipschitz等价方面[5,6]、重分形方面[7,8]、拟同胚方面[9,10]等多方面都有重要的发展和应用。在这些应用中,齐次Moran集是重要的一部分。构造了平面上一类特殊的齐次Moran集,并计算出了它们的Packing维数下界。

(1) Iφ=I;

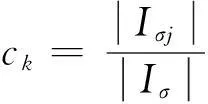
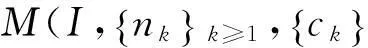
若Iσ1与Iσ有相同的左端点,Iσnk与Iσ有相同的右端点,且Iσi之间的间隔相等,则E又称为齐次Cantor集,记为C。
若Iσ1与Iσ有相同的左端点,对于1≤i≤nk-1,Iσ(i+1)的左端点与Iσi的右端点相同,则E又称为偏齐次Cantor集,记为C*。
齐次Cantor集与偏齐次Cantor集是两类特殊但非常重要的齐次Moran集。
关于一维齐次Moran集的Packing维数,文献[11]中证明了下面的结果:
定理1任给E∈M,有
s*≤dimPE≤t*。
特别地
dimPC*=s*,dimPC=t*,
其中:
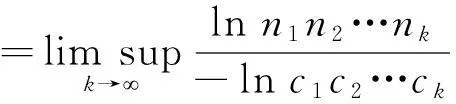
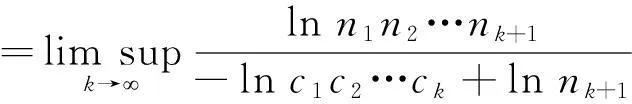
C,C*分别表示齐次Cantor集,偏齐次Cantor集。
我们试图把此结果推广到二维平面上一类特殊的齐次Moran集上,证明得到了它们Packing维数的下界。
2 一类特殊齐次Moran集
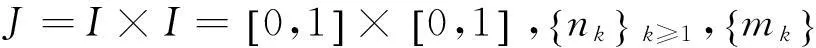
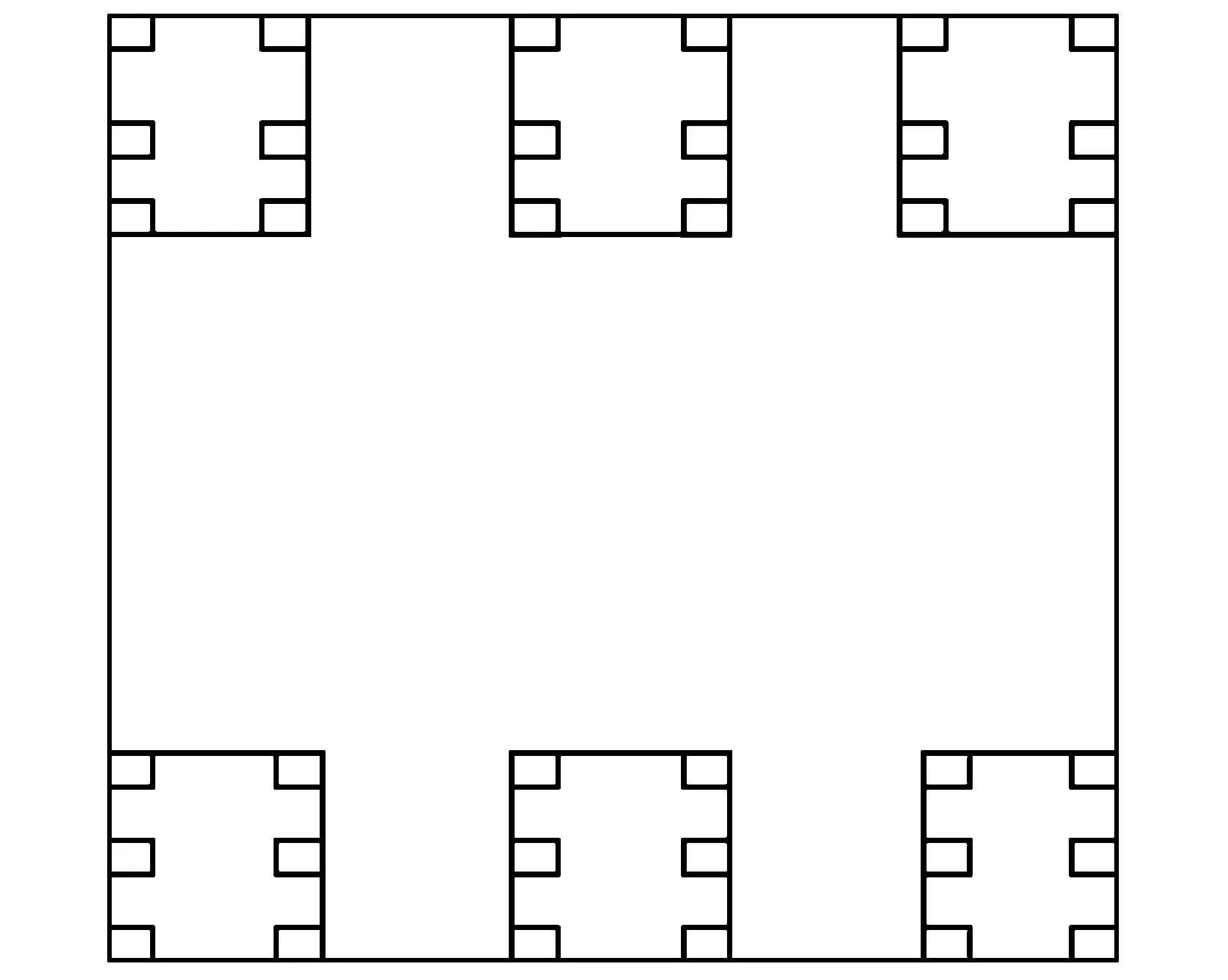
图1 平面上齐次Moran集的构造Fig.1 Homogeneous Moran set construction in plane
图1中,(n1,m1,c1)=(3,2,1/5),(n2,m2,c2)=(2,3,1/5)。
定理2任给
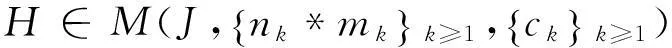
有dimPH≥l*,其中:
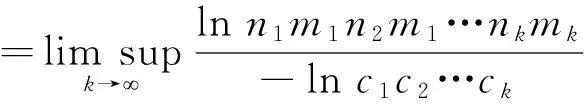
证明设μ是支撑在H上的概率测度,且对H的任意k阶基本区间Ak,μ(Ak)=(n1m1n2m1…nkmk)-1。对任意的x∈H,记B(x,c1c2…ck)为中心在x,边长为c1c2…ck的正方形,它至少包含一个H的k阶基本正方形,并至多与9个H的k阶基本正方形相交,因此,有
(n1m1n2m1…nkmk)-1≤μ(B(x,c1c2…ck))≤9(n1m1n2m1…nkmk)-1,
于是,有
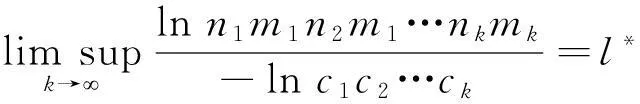
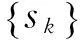
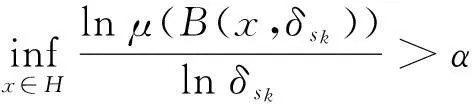
其中:δsk=c1c2…csk。因此,对任意x∈H,当k>N时,有
μ(B(x,δsk))≤(δsk)α。
(1)
对任意子集M⊂H,用N(δsk,M)表示中心在M中,边长为δsk且两两不交的正方形的最大个数,记B(xi,δsk),xi∈M,i=1,2,…,N(δsk,M)为这些不交的正方形,于是{B(xi,2δsk)}是M的一个覆盖。注意到B(x,2δsk)至多与16个边长为δsk的正方形相交,所以有

(2)

(3)
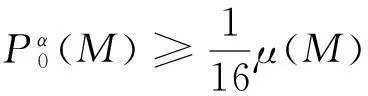
(4)
[1]Feng D J,Hu H Y.Dimension Theory of Iterated Function Systems[J].Comm.Pure Appl.Math,2009,62:1 435-1 500.
[2]Feng D J.The Limited Rademacher Functions and Bernoulli Convolutions Associated with Pisot Numbers[J].Adv.Math,2005,195:24-101.
[3]Wang B W,Wu J.Hausdorff Dimension of Certain Sets Arising in Continued Fraction Expansions[J].Adv.Math,2008,218:1 319-1 339.
[4]Wu J.On the Sum of Degrees of Digits Occurring in Continued Fraction Expansions of Laurent Series[J].Math.Proc.Cambridge Philos.Soc,2005,138:9-20.
[5]Rao H,Ruan H J,Wang Y.Lipschitz Equivalence of Cantor Sets and Algebraic Properties Ofcontraction Ratios[J].Trans.Amer.Math.Soc,2012,364:1 109-1 126.
[6]Rao H,Ruan H J,Xi L F.Lipschitz Equivalence of Self-similar Sets[J].C.R.Math.Acad.Sci.Paris,2006,342:191-196.
[7]Li J J,Wu M.Pointwise Dimensions of General Moran Measures with Open Set Condition[J].Sci.China Math,2011,54:699-710.
[8]Wu M.The Singularity Spectrumf(α) of Some Moran Fractals[J].Monatsh.Math,2005,144:141-155.
[9]Peng F J,Wen S Y.Fatness and Thinness of Uniform Cantor Sets for Doubling Measures [J].Sci.China Math,2011,54:75-81.
[10]Wang X H,Wen S Y.Doubling Measures on Cantor Sets and Their Extensions[J].Acta Math,2012,134:431-438.
[11]Feng D J,Wen Z Y,Wu J.Some Dimensional Results for Homogeneous Moran Sets[J].Science of China(Series A),1997,40:475-482.
[12]Falconer K.Fractal Geometry-mathematical Foundation and Applications[M].New York:John Wiley and Sons,1990.
[13]胡晓梅.k分Cantor集Ck上p方可积函数空间LP(Ck,μ)的可分性[J].甘肃科学学报,2010,22(2):153-155.
Packing Dimension of First-Class Special Homogeneous Moran Set in Plane
Hu Xiaomei1,2
(1.School of Mathematics and Statistics,Hubei University of Science and Technology,Xianning 437100,China;2.School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China)
This article builds a first-class special homogeneous Moran set in plane to prove the lower bound of Packing dimension by analyzing the structure and utilizing calculation methods and techniques of dimension in fractal geometry.
Homogeneous Moran set;Packing dimension;Lower bound
10.16468/j.cnki.issn1004-0366.2016.04.002.
2015-05-12;
2015-07-20.
国家自然科学基金资助项目(11271148);湖北科技学院校级资助项目(2013-XB-013).
胡晓梅(1979-),女,湖北咸宁人,副教授,研究方向为分形几何.E-mail:xiaomeihu@163.com.
O174.12
A
1004-0366(2016)04-0006-03
引用格式:Hu Xiaomei.Packing Dimension of First-Class Special Homogeneous Moran Set in Plane[J].Journal of Gansu Sciences,2016,28(4):6-8.[胡晓梅.平面上一类特殊齐次Moran集的Packing维数下界[J].甘肃科学学报,2016,28(4):6-8.]
