一种平面轮廓分割与基元识别方法研究*
2016-08-31李欣言杜文华王俊元段能全
李欣言 杜文华 王俊元 段能全 关 波 汤 恒 李 博
(中北大学机械与动力工程学院,山西 太原 030051)
一种平面轮廓分割与基元识别方法研究*
李欣言杜文华王俊元段能全关波汤恒李博
(中北大学机械与动力工程学院,山西 太原 030051)
为提高视觉测量系统的检测精度与检测速度,提出了一种平面轮廓分割与识别算法。首先对经过多边形逼近算法进行轮廓分割获得的分割点位置按一定规则进行修正;然后对分割点间的线段类型加以识别,对过度分割的圆弧段进行融合处理;最后用加权最小二乘拟合算法抑制了大的离群值的影响,将轮廓拟合成相对应的几何基元。对提出的方法分别进行检测精度与检测速度对比实验和基元识别能力测试实验。实验结果表明,提出的方法基元识别准确、检测速度快、通用性好。
机器视觉;轮廓分割;基元识别;多边形逼近
近年来,随着机器视觉技术测量精度及测量速度的提高,其在机械零件尺寸[1]、刀具[2]参数测量等方面的应用越来越多。这些三维零件、刀具在采用视觉技术进行测量时,被检测图像经边缘检测后获得主要由直线、圆弧、圆等基元构成的平面轮廓。平面轮廓基元识别是检测系统必不可少的关键环节,识别的准确性直接影响后续尺寸测量的精度;识别的效率直接影响检测系统的实时性。因此在进行视觉处理中需要对这些平面轮廓进行精确的分段识别和重构。
对由测量设备获取的二维轮廓进行分段与识别,国内外有很多学者进行了相应的研究。Jayachandran A[3]提出了基于模糊逻辑的图像处理新方法和新思想,用模糊推理来检测角,有效地抑制了图像噪声,取得了良好的效果。徐越[4]为实现重叠目标的精确分割,提出了一种Snake模型与角点检测相结合的重叠目标分割方法。郑军等[5]针对轮廓曲线的多边形近似和特征点提取,提出了多边形逼近误差和局部最小误差逼近特征点的定义和相应的实现算法。顾步云[6]针对包含直线、圆弧特征的截面轮廓数据,通过计算离散点曲率进行特征点的提取与数据分段。王英惠[7-9]在文献[7-8]中分别用近似曲率的十一点法和曲率差分图的方法进行平面轮廓的精确分段与识别;在文献[9]中采用约束最小二乘算法对轮廓进行了重构。伍济钢[10]用HOUGH变换改进的曲率法来识别平面轮廓图元。胡魁贤[11]以线段和圆弧为逼近基元对封闭的截面曲线进行分段拟合,该算法简单有效,较好地解决以直线和圆弧为基元的截面曲线拟合问题。张习文[12]以线段和圆弧为逼近基元,研究基于改进遗传算法的曲线拟合,较好地解决了用线段和圆弧拟合曲线问题。在深入研究现有平面轮廓分段识别与重构等方法的基础上,本文提出了一种新的平面轮廓分割与基元识别方法。
1 基元识别算法的思路
采用多边形近逼近算法将轮廓曲线进行分割,找出边界轮廓的分割点;针对该算法分割点不精准的缺点,采用一种规则对该分割点的位置进行判别,如不符合条件则进行修正;然后对基元进行识别,对圆弧段轮廓是否过度分割进行判别,如属于过度分割则对其进行融合;最后采用拟合算法对分割后的轮廓进行拟合。
2 轮廓分割与基元识别算法的方法
2.1分割点位置修正
采用多边形近逼近算法将通过测量系统获取的被测物体的平面轮廓曲线进行分割。由于多边形逼近算法获得的分割点与阈值的选取有关,导致多边形控制点与图像真实拐点之间产生偏差,最终影响轮廓的准确识别。现对此分割点进行修正。
如图1所示,S为一段平面轮廓,A、O、B为经多边形近逼近算法获得的分割点。SAO、SOB为分割后的轮廓,dAO、dOB分别为该轮廓段与所对应的逼近多边形的边AO、OB之间的最大距离。
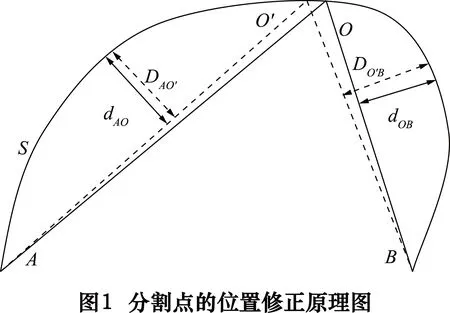
判断dAO、dOB的大小:
①当dAO>dOB,则将分割点O向SAO段移动一个轮廓控制点到点O′。SAO′、SOB′为分割后的轮廓,DAO′、DO′B分别为重新分割后的轮廓段与所对应的逼近多边形的边AO′、O′B之间的最大距离。
判断:若Max{DAO′,DO′B}>Max{dAO,dOB},则不做处理,此分割点O保留;
若Max{DAO′,DO′B}
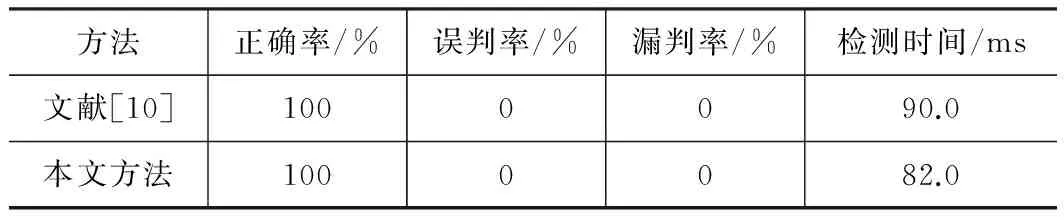
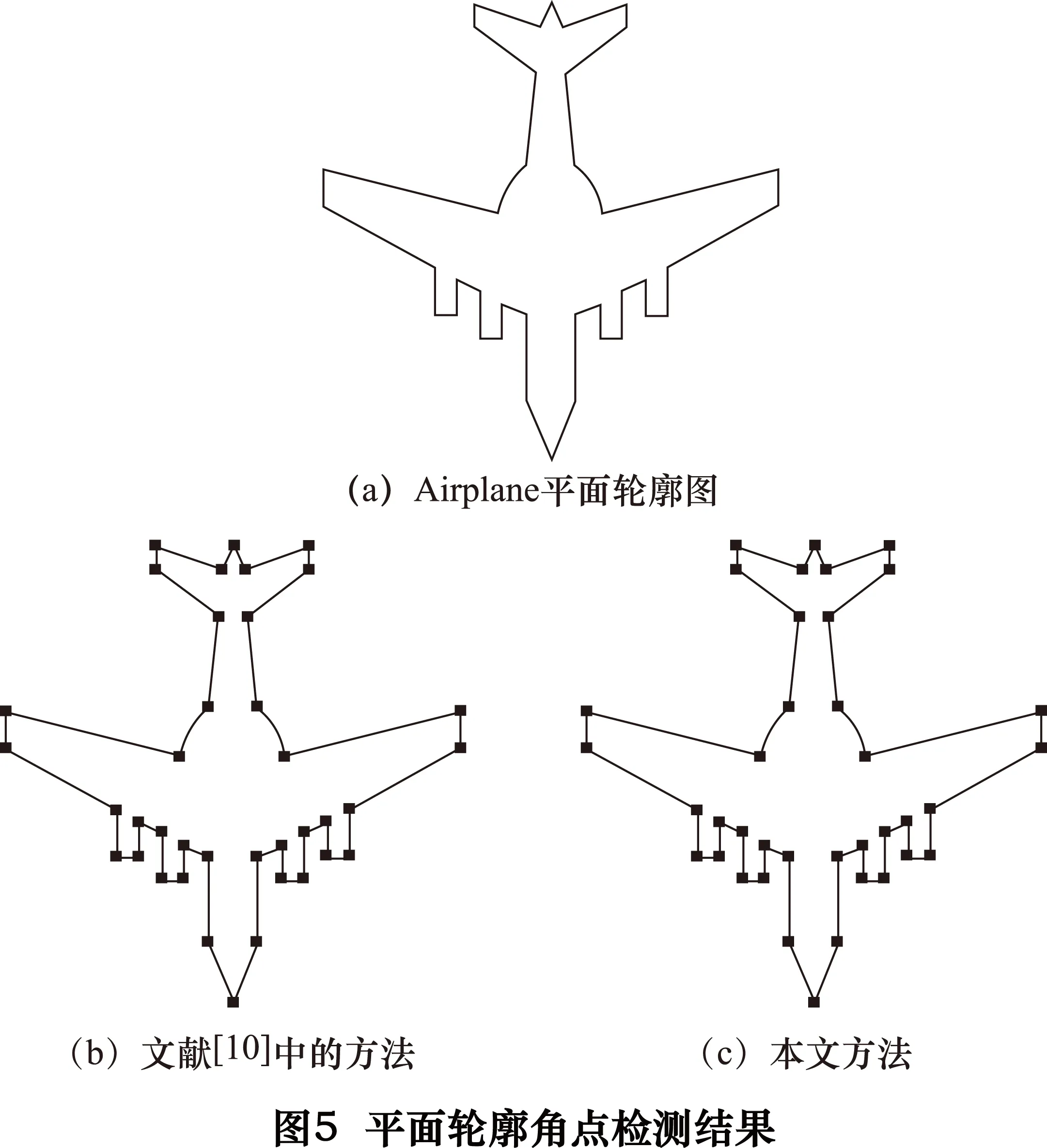
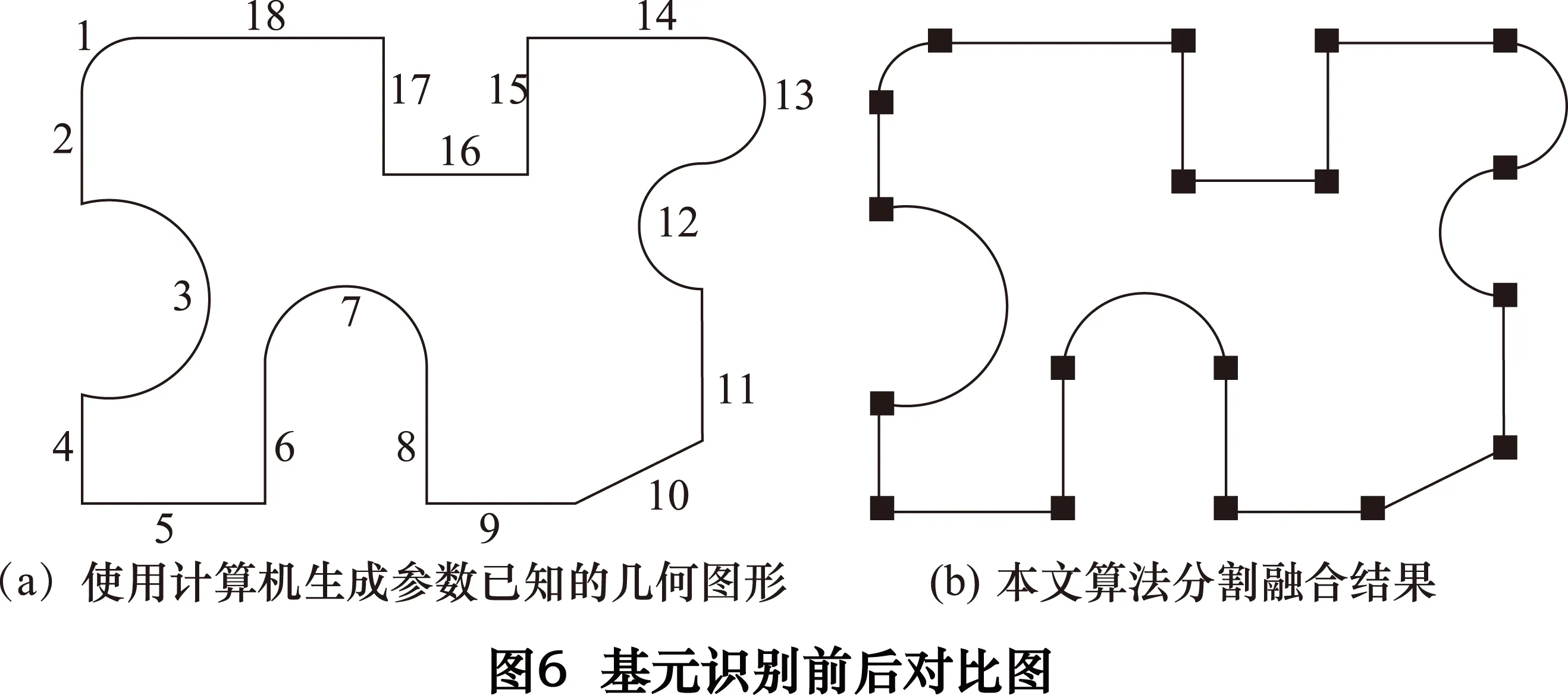
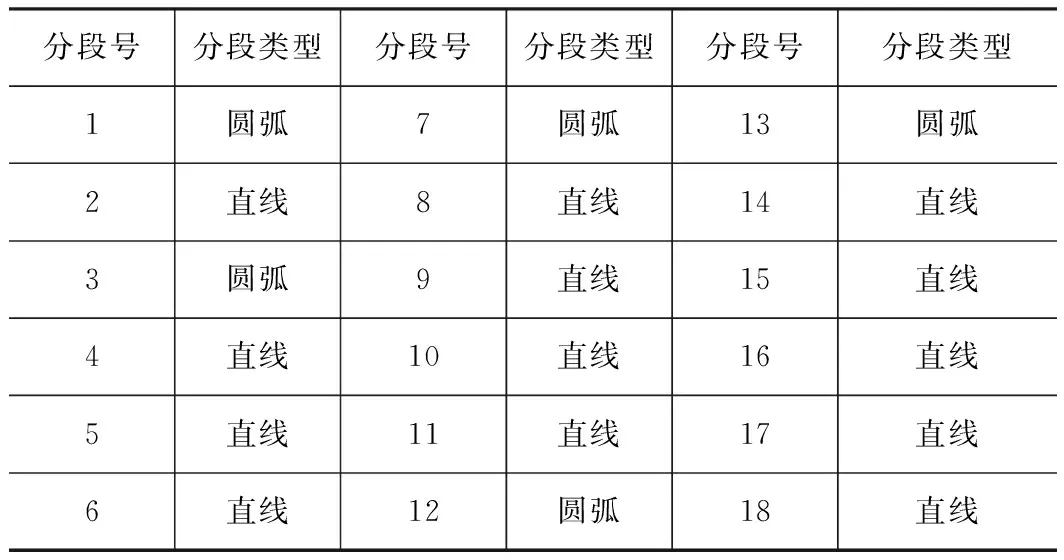
② 当dAO ③ 依此方法再进行下一个分割点的修正,直至全部分割点都修正完毕。 2.2基元识别与轮廓段的融合 经过多边形近逼近后,轮廓中的有些圆弧段处于过度分割状态,因此需要对这些圆弧段进行检测,如属于过度分割,则需要进行融合。取原始轮廓S上的4个分割点A、B、C、D,如图2所示。 Q是由点A、B、C拟合得到的圆弧段,其一般式方程为: Q={(x,y)|x2+y2+D·x+E·y+F=0} (D2+E2-4F>0) (1) 设分割点A、B、C的坐标分别为(xa,ya)、(xb,yb)、(xc,yc),代入式(1)可求得方程的系数: 设圆弧段Q的圆心坐标为O,半径为ρ,由式(1)可得: ki(xi,yi)是轮廓SAC段上的任一控制点,计算其到圆心O(xo,yo)的距离与圆弧半径ρ之差: hmax=Max(hi) 设hi是轮廓SAB与对应的多边形边AB的最大距离,d2是轮廓SBC与对应的边BC的最大距离。 若hmax 2.3加权最小二乘拟合算法 为了表征轮廓信息,提取轮廓参数,需要对分割后的轮廓段进行拟合。最小二乘法是一种较常用的方法。当轮廓边缘存在大的离群值时,由于最小二乘法采用的是平方距离,那些与拟合线距离较远的点在拟合过程中会拥有非常大的权重,导致其鲁棒性差。 考虑离群值的影响,在进行拟合计算时为每个点引入Tukey[13]权重系数ωi,进行直线拟合时以: 为目标函数,对直线参数α、β、γ进行优化,式中λ为拉格朗日乘数。 图3为一刀具测量图像,图中的凸起为未擦拭干净的切屑。采用上述算法进行五次迭代后的拟合直线,基本上排除了大的离群值对原轮廓线的影响。 对圆弧形轮廓段拟合时以: 为目标函数,对圆弧参数α、β、ρ进行优化。图4为轮廓分割与基元识别的算法流程图。 3.1平面轮廓角点的检测精度与检测速度的对比分析 有些平面轮廓中的特征点的类型为角点,如文献[10]中的Airplane图像,图5a所示。分别用文献[10]中的改进的曲率法及本文提出的方法对其进行特征点检测,检测结果如图5b、c所示。 Airplane轮廓共有38个特征点,对上述2种特征点检测方法的正确率、误判率、漏判率、检测时间进行对比分析,结果如表1所示。 表1 Airplane 图像平面轮廓特征点检测效果 从表1可以看出,本文提出的方法同样能100%检测出轮廓中的特征点,且检测时间少于文献[10]中的方法。在某些在线实时测量过程中,需要在有限的时间内对大量图片进行处理,利用本文提出的方法可以更好地满足此类需求。 3.2平面轮廓的特征点检测 为了测试本文提出的方法对其他类型的特征点的检测能力以及特征点检测的精确程度,采用文献[6]、[10]中使用的平面轮廓图像,如图6a所示。图6b为经本文算法进行基元识别后的结果,■表示识别出的特征点,不同基元以不同灰度区分开。表2为分段数据的曲线类型判断结果。 表2 分段数据的曲线类型判断结果 上述结果表明了利用本文算法所提取的特征点精度较高,几乎不存在“伪”特征点。并且准确地识别了相邻特征点之间的分段轮廓的基元属性。 本文提出了一种将平面轮廓按照几何基元分割为直线和圆弧的算法。该算法能准确识别平面轮廓中的直线、圆弧,且计算速度较快。在刀具在线实时测量中有较好的应用。 [1] 李红钢,杜文华,曾志强,等.基于机器视觉的圆筒形零件直角梯形槽槽宽检测研究[J].包装工程,2013(3):83-87. [2]王飞,杜文华,关波,等.基于视觉的刀具参数高精度测量[J].计算机工程与设计,2015(2):524-528. [3]Jayachandran A, Dhanashakeran R, Sugel Anand O.Fuzzy information system based digital image segmentation by edge detection Source[C].2010 IEEE International Conference on Computational Intelligence and Computing Research:IEEE Computer Society,2010:794-798. [4]Xu Yue,Li Yinghui,Song Huaibo.Segmentation method of overlapped double apples based on Snake model and corner detectors[J]. Nongye Gongcheng Xuebao/Transactions of the Chinese Society of Agricultural Engineering,2015,31(1):196-203. [5]郑军,刘正文,马兆瑞,等.基于最小误差逼近的轮廓特征点提取[J].清华大学学报:自然科学版,2008,48(2):165-168. [6]顾步云,周来水,李涛.一种新的截面轮廓特征点识别与分段曲线类型判别算法[J]. 机械科学与技术,2007,26(11):1398-1402. [7]王英惠,吴维勇,赵汝嘉.平面轮廓的分段与识别技术[J].计算机辅助设计与图形学学报,2002,14(12):1142-1145. [8]吴维勇,王英惠,周晏.平面轮廓识别与分段技术的研究与快速实现[J].图学学报,2003,24(14):14-19. [9]王英惠,吴维勇.基于分段与识别技术的平面轮廓的精确重构[J].图学学报,2007,28(5):43-48. [10]伍济钢,宾鸿赞.用HOUGH变换改进的曲率法识别平面轮廓图元[J].图学学报,2011,32(2):102-106. [11]胡魁贤,严宏志,朱自冰,等.截面轮廓曲线分段约束拟合[J].计算机工程与科学,2009(7):53-56. [12]张习文,欧宗瑛.基于遗传算法的以线段和圆弧为基元的曲线拟合[J].计算机辅助设计与图形学学报,2002,14(2):144-147. [13]Mosteller F,Tukey J W .Data analysis and regression[M].Reading,MA:Addison-Wesley,1977. (编辑孙德茂) 如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。 Research on the method of planar contour segmentation and recognition of the geometric primitives LI Xinyan, DU Wenhua, WANG Junyuan, DUAN Nengquan, GUAN Bo, TANG Heng, LI Bo (School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, CHN) In order to improve the detection accuracy and speed of the vision measurement system, a method of planar contour segmentation and recognition is proposed. First, the position of the points of division obtained by the polygon approximation algorithm is modified by a certain rule. Then the types of line segments between the points are identified, and the over segmented arc is combined. In the end, the affect of large outliers is limited by the weighted least squares fitting algorithm. And the contour is synthesized into the corresponding geometric elements. Experimental demonstration of the proposed method is carried out by testing accuracy and speed detection contrast experiments and identification ability of basic element experiments. Experimental results show that the proposed method has the characteristics of high accuracy, fast detection speed and good generality. machine vision; contour segmentation; primitive recognition; polygon approximation TP391 A 李欣言,女,1989年生,硕士研究生,主要研究方向为机器视觉、图像处理。 2015-09-15) 160121 *山西省研究生优秀创新资助项目(20133095)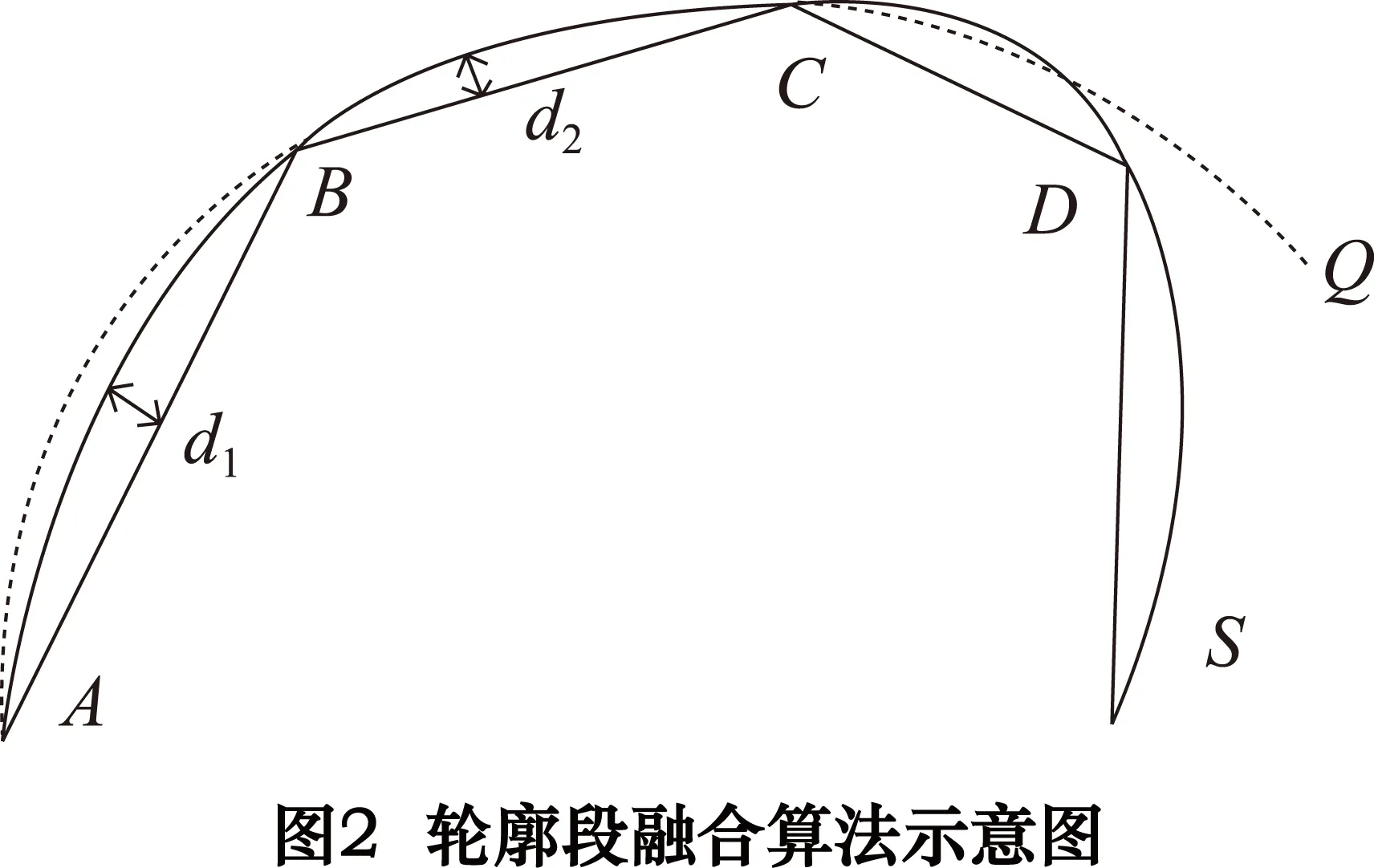

3 实验结果及分析
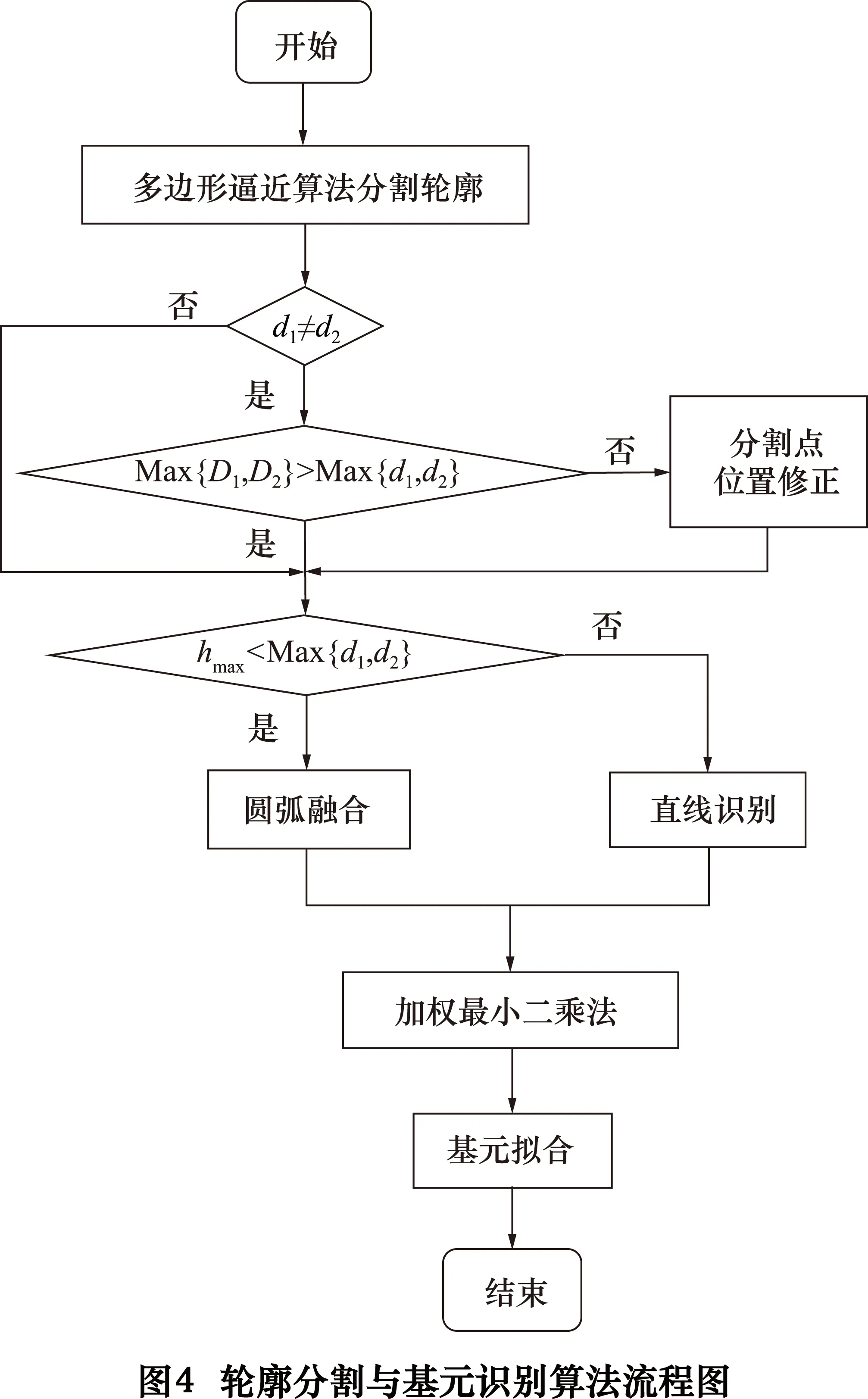
4 结语
