利用小尺寸缺口试样测定延性材料的单轴本构关系

尹　涛,　蔡力勋,　陈　辉，　包　陈

(西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室， 成都 610031)



利用小尺寸缺口试样测定延性材料的单轴本构关系

尹涛,蔡力勋,陈辉，包陈

(西南交通大学 力学与工程学院 应用力学与结构安全四川省重点实验室， 成都 610031)

提出了一种利用三点弯曲试样获取延性材料本构关系的测试方法：针对小尺寸缺口试样的三点弯曲线载荷-位移曲线，采用有限元辅助测试 (Finite-element-analysisaidedtests，FAT) 方法，迭代获得材料代表性体积单元(Representativevolumeelement，RVE)本构关系。研究表明，两种延性材料的有限元迭代反求结果和单轴拉伸试验结果吻合较好。应用该方法，可以采用小尺寸缺口试样来获取延性材料的本构关系。

FAT方法；单轴本构关系；小尺寸试样；缺口试样；三点弯曲

基于小尺寸试样获取航空、核电、化工及电子精密设备用材料的本构关系对结构设计和服役安全评价具有重要价值。近二十年来通过小尺寸试样获取金属材料力学性能的理论和测试方法受到重视，但至今仍存在诸多困难。为获取纳米尺度下材料的力学参数，文献[1～8]通过改进试件和测试技术，采用单轴拉伸实验方法测试了材料的杨氏模量、屈服强度和抗拉强度。到目前为止Olive等[9]提出的纳米压痕测试方法在小尺度材料的力学性能测试上应用较为广泛，由于其理论须依赖载荷-压入深度曲线的非线性卸载部分而存在较大的测试误差，该方法并未推广应用于结构材料性能的测试；Beams等[10]提出的鼓膜实验方法可以测得薄膜的残余应力、弹性模量、屈服强度和断裂强度，因受试薄膜的残余应力须为拉应力，故此方法存在一定的局限性；Weihs等[11]提出的悬臂微梁弯曲法，利用压头对悬臂梁加载测得微梁的弹性模量、屈服强度和断裂强度，但是在实验过程中微梁厚度的测量精度不易确保且压头

沿梁长方向产生移动误差，因而实验结果的精度受到限制；Osterberg等[12]提出的M-Test微梁弯曲法仅能测得弹性模量。上述方法都试图针对纳米尺度材料开展力学性能测试，许多实验结果会出现不同程度尺寸效应，很难应用于毫米、厘米级尺寸试样。当传统分米级尺寸单轴拉伸试样不能用于获取毫米级尺寸材料的力学性能时，发展基于毫米、厘米级小尺寸非标准试样的材料力学性能测试方法具有重要应用价值。

本研究提出采用三点弯曲小尺寸缺口试样，基于试样的线载荷-位移试验结果与有限元分析结果相耦合的FAT方法[13-14]获取延性金属材料的单轴本构关系。

1　试验条件

1.1材料、试样与夹具

试样材料为1Cr12Mo钢和P92钢，其化学成分分别由表1、表2给出。

表1　1Cr12Mo钢化学成分(质量分数/%)Table 1　Chemical composition of 1Cr12Mo steel(mass fraction/%)

图1为等直拉伸圆棒试样，用于获取1Cr12Mo钢、P92钢材料的单调拉伸应力应变关系和常规机械性能。

单调拉伸试验采用MTS809 250KN试验机，控制器为MTSTestStar，控制软件为MTSTestStarⅡ，引伸计采用632.54F-14，测得1Cr12Mo钢、P92钢材料的拉伸性能由表3给出。

表2　P92钢化学成分(质量分数/%)Table 2　Chemical composition of P92 steel (mass fraction/%)

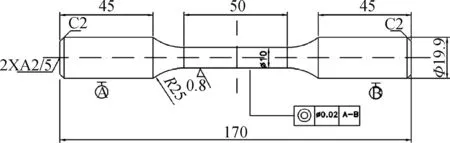
图1　等直拉伸圆棒试样Fig.1　Equivalent round bar tensile specimen

表3　1Cr12Mo钢和P92钢拉伸性能Table 3　Mechanical character of 1Cr12Mo steel and P92 steel

图2为缺口试样构型，由数控机床精密加工而成并对其外表面进行抛光处理。试样采用三点弯曲加载，夹具构型如图3，4所示。夹具材料采用的是经过表面淬火处理的硬质合金钢。滚轮直径为10mm，轮轴直径为3mm。在上、下夹具及滚轮上采用数控机床精密刀刻出图3、图4中②，③，④，⑤，⑥ 5组刻线。④为从距下夹具中心线5mm处开始，向两侧每隔2mm的平行刻线组，⑤为在滚轮侧面两组相互垂直的刻线组，滚轮轮表面的刻线⑥为⑤的延长线，所有基准线均采用数控机床精密刀刻刻出。

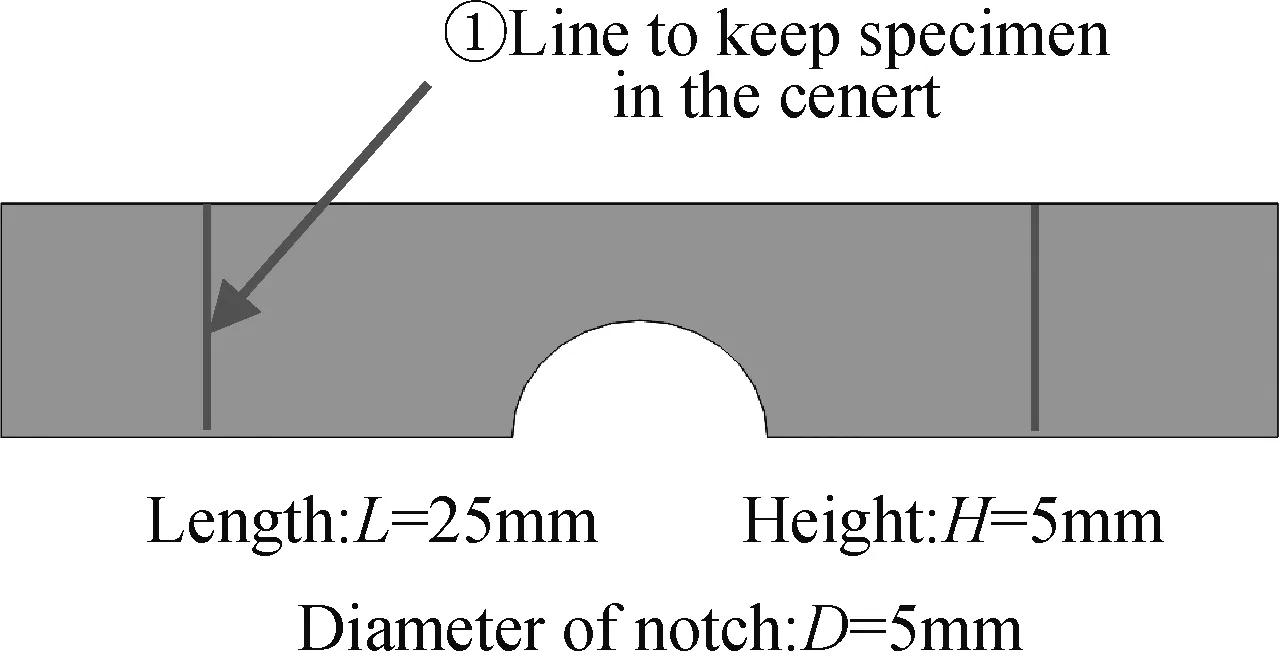
图2　缺口试样Fig.2　Notched specimen

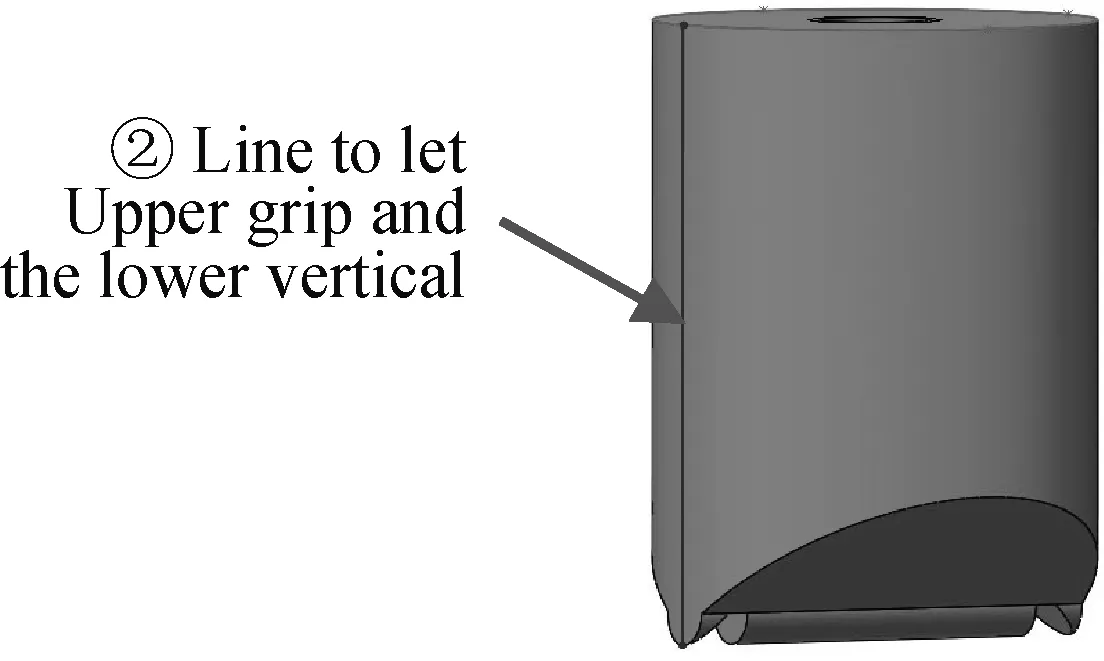
图3　夹具上夹头Fig.3　Upper grip

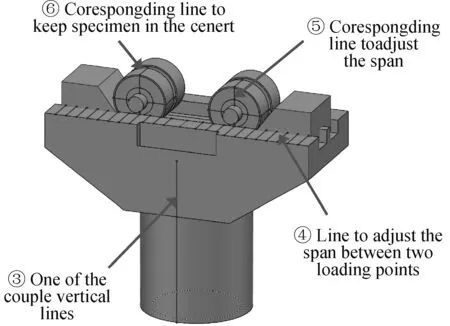
图4　夹具下夹头Fig.4　Lower grip

图5示出了实际试验装置。在试验装配过程中，刻线②和刻线③用于上、下夹具的对中和垂直；刻线④和刻线⑤用于调整两组滚轮中心点之间的距离，因为缺口试样与下夹头的接触点在轮轴的顶端，故刻线④和刻线⑤可用于调整三点弯试样两个下接触点的跨距；刻线①和刻线⑥用于调整试样在轮轴上安放对中。

图5　缺口试样三点弯曲试验夹具及试样装配图Fig.5　Grips assembling of notched specimen in three-point bending test

1.2试验设备

缺口试样的三点弯曲试验设备为MTSAcumen1kN材料试验机，控制器为MTSFlexTest40，控制软件为MTSSeries793。考虑到上夹具和MTS作动轴刚度很高，且三点弯曲试样的柔度大，故直接采用MTS的光栅式位移传感器测得压头与试样接触点处的位移。

三点弯曲试验中缺口试样两个下接触点的跨距为18mm。试验采用位移控制，加载速率为0.01mm/s，对材料1Cr12Mo钢和P92钢各3个缺口试样加载至最大位移1.7mm，试验中采集得到试样的线载荷-位移曲线。

2　试验结果

材料1Cr12Mo钢和P92钢各3个试样的三点弯曲试验线载荷-位移曲线由图6给出，所示两种材料各三个试样的试验结果重合度较高，说明材料1Cr12Mo钢和P92钢分散性较小，各向同性条件好，利于结合有限元方法获取材料本构关系。

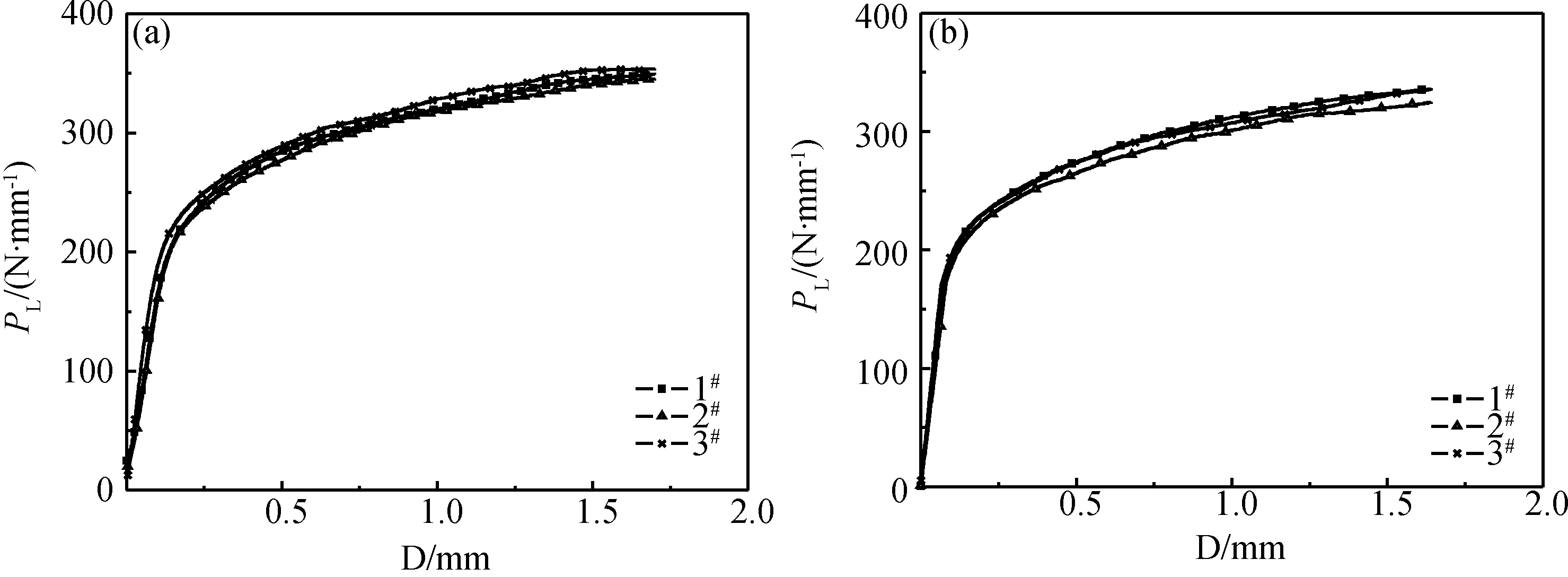
图6　1Cr12Mo钢(a)和P92钢(b)缺口试样三点弯曲试验PL-D曲线Fig.6　Linear load-displacement curves of notched specimens under three-point bending tests for 1Cr12Mo steel(a) and P92 steel (b)

3　研究方法

3.1FAT方法

通过图5所示的缺口小试样的三点弯曲试验，可以获得试样的线载荷-位移曲线，再通过有限元迭代计算，使得试样的模拟线荷载-位移曲线与三点弯曲试验获得的线荷载-位移曲线趋近重合，进而反求获得材料的单轴本构关系，这种方法为有限元辅助测试方法，即FAT方法。

3.2Hollomon材料本构模型

经典的单轴本构模型用少数几个参量就可以很好地描述材料的弹塑性变形行为。尽管不同材料发生塑性变形的机制不尽相同，但绝大多数金属材料都近似符合幂律硬化[15]，其单轴应力-应变关系可表示为：

(1)

式中：E为弹性模量，K为应变硬化系数，n为应变硬化指数，σy为屈服强度。

在ANSYS中可以直接使用上述幂律硬化本构关系作为FAT迭代计算的初值来进行仿真分析，便于对有限元模型的精度检验、排除弱影响量。

3.3缺口试样的有限元网格模型

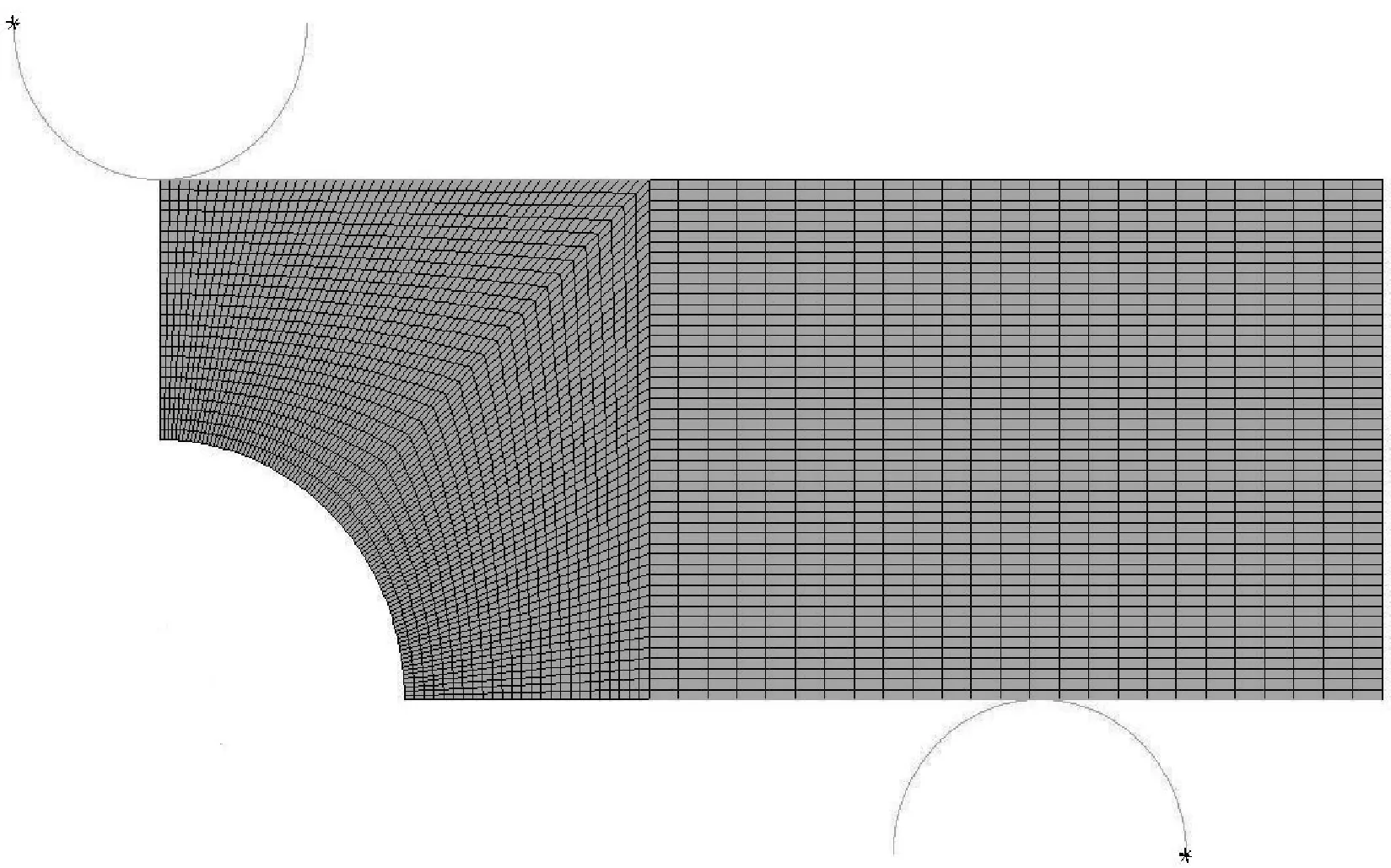
图7　弹塑性有限元网格模型Fig.7　The elastoplastic finite model of semi-model

在有限元模拟时，不考虑缺口试样和上、下夹具的上下接触点及滑轮与下夹具表面的摩擦系数，假设缺口试样材料为均匀连续、各向同性、率无关，且遵循Mises屈服准则和Voce等向强化准则。缺口试样三点弯曲试验荷载具有轴对称性，故利用Ansys对三点弯曲缺口试样进行试验模拟分析时，可建立单位厚度的2D半模型。在带厚度的平面应力框架下选用Plane182单元。有限元模型网格划分时，对圆弧缺口的部分进行网格加密，共得到3859个单元，如图7所示。上、下夹头荷载定义为集中荷载，并使下夹头接触点单元位移耦合固定，上夹头接触点约束横向位移为零，竖向位移为1.7mm，从而实现模拟的弹塑性线荷载-位移关系曲线获取。

为了验证在平面应力的条件下采用单位厚度2D半模型模拟小尺寸缺口试样三点弯曲试验计算得到的线载荷-位移曲线的精度，建立1Cr12Mo和P92两种材料缺口试样2D半模型和厚度为1.5mm的3D半模型，代入由单调拉伸试验测得的单调拉伸应力应变关系进行有限元计算，提取线载荷-位移曲线并与缺口试样对应的三点弯曲试验曲线进行比较，如图8所示。

由图9可以看出，由单位厚度2D半模型和3D半模型计算得到的线载荷-位移曲线与两种材料的各3个试样的实验曲线重合度高。故可以得出，在平面应力的条件下，采用单位厚度半模型模拟小尺寸缺口试样的三点弯曲试验来获取的线载荷-位移曲线并不影响其计算精度。

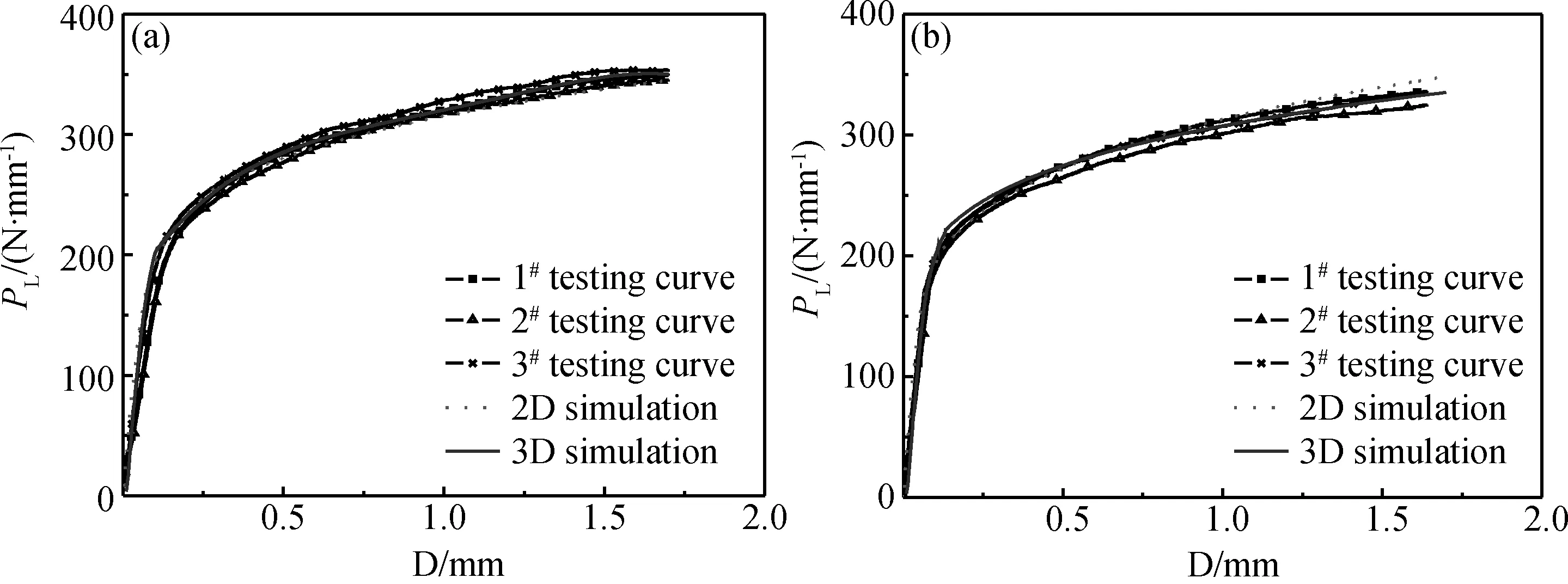
图8　1Cr12Mo钢(a)和P92(b)钢缺口试样三点弯曲试验PL-D曲线和有限元计算PL-D曲线的比较Fig.8　Comparison of experimental curves under three-point bending tests and computational curves for 1Cr12Mo steel(a) and P92 steel (b)

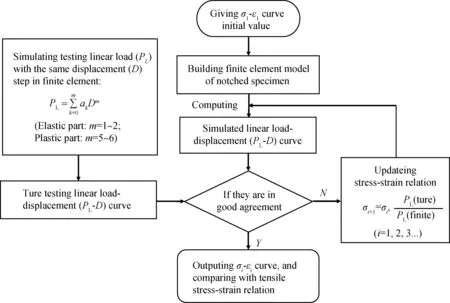
图9　FAT方法流程框图Fig.9　The flow chart of FAT method

3.4获取材料本构关系的FAT方法

通过结合有限元迭代得到与试验线载荷-位移曲线重合的有限元模拟线载荷-位移曲线，从而获取金属材料本构关系。计算流程图如图9所示。

4　FAT分析结果

对于两种材料1Cr12Mo和P92三点弯曲缺口小试样的试验结果开展有限元模拟迭代求解，给定Hollomon本构模型参数初值为K=1200MPa，n=0.2。按照图9所示流程经过3～5次迭代收敛时，得到PL-D曲线如图10和图12所示、压头与试样接触点处的σ-ε曲线如图11和图13所示。图11和图13中1Cr12Mo钢和P92钢的单调拉伸σ-ε曲线由图1所示的等直拉伸圆棒试样获取。

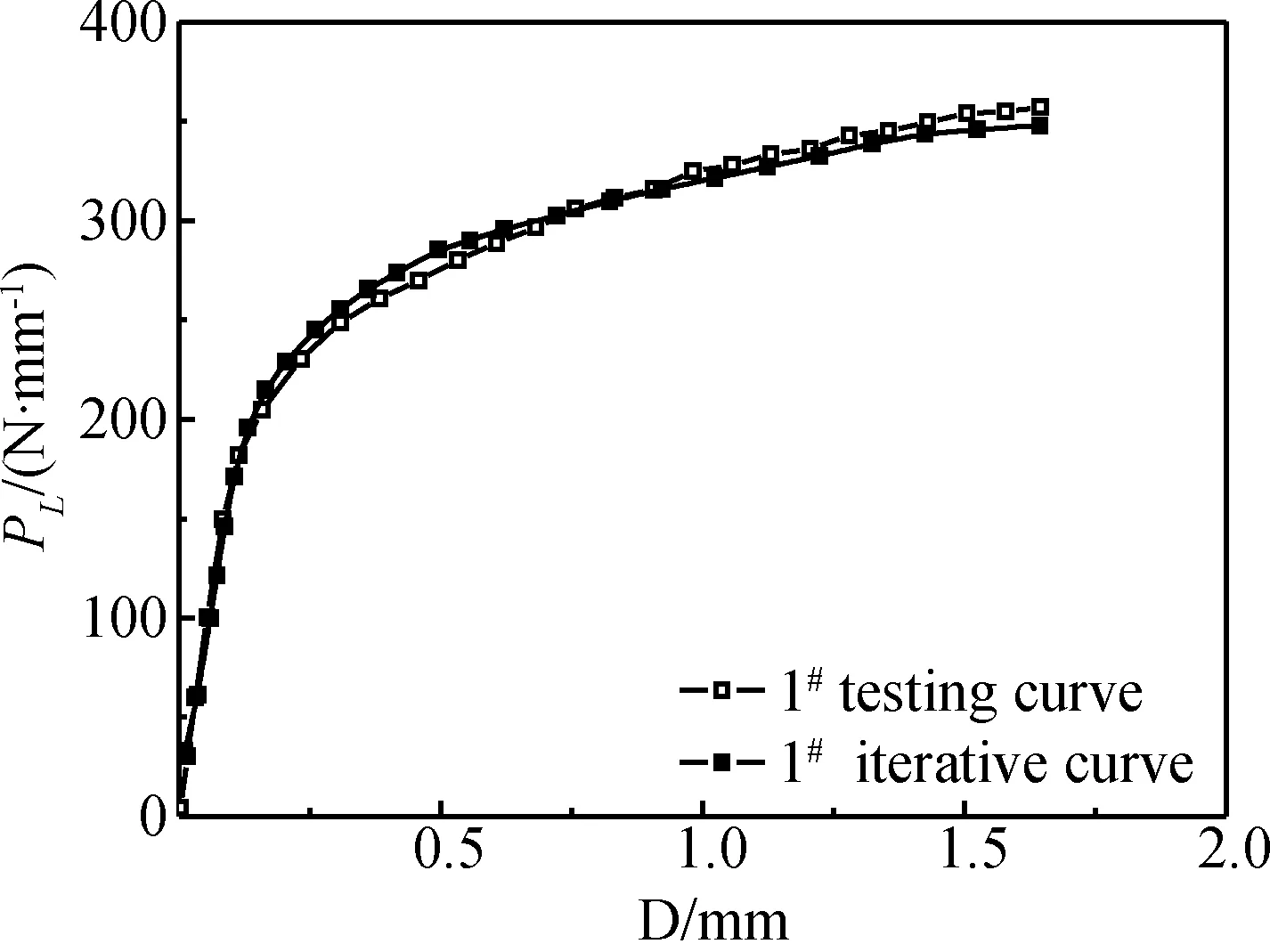
图10　迭代收敛时1Cr12Mo钢的PL-D曲线Fig.10　Comparison of experimental and iterative curves for 1Cr12Mo steel

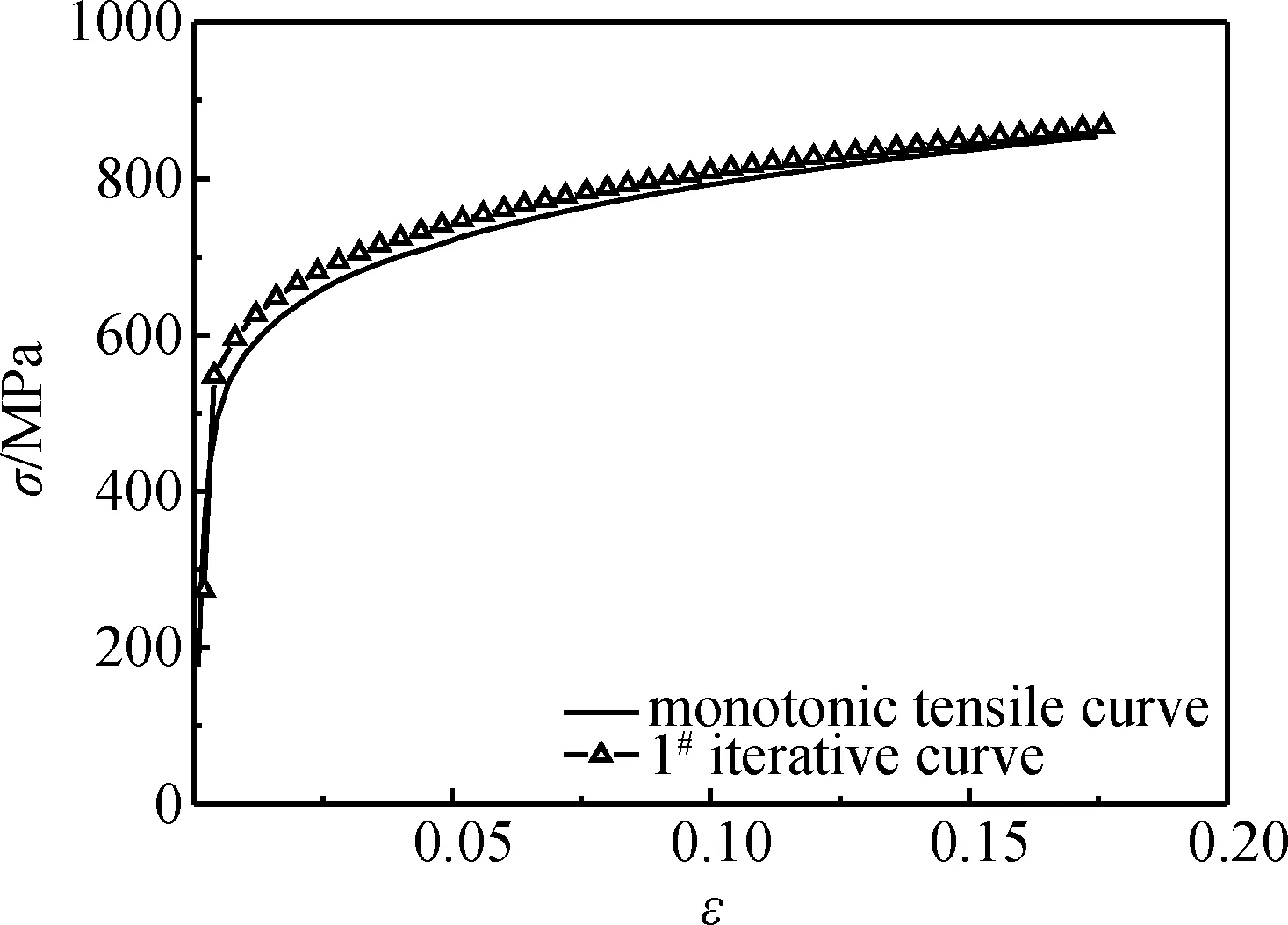
图11　迭代收敛时1Cr12Mo钢的单调拉伸的σ-ε曲线Fig.11　Comparison of experimental and uniaxial tensile curves for 1Cr12Mo steel

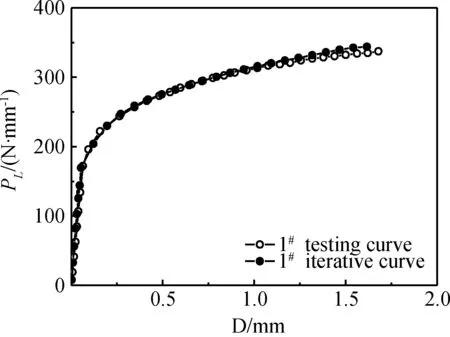
图12　迭代收敛时P92钢的PL-D曲线Fig.12　Comparison of experimental and iterative curves for P92 steel

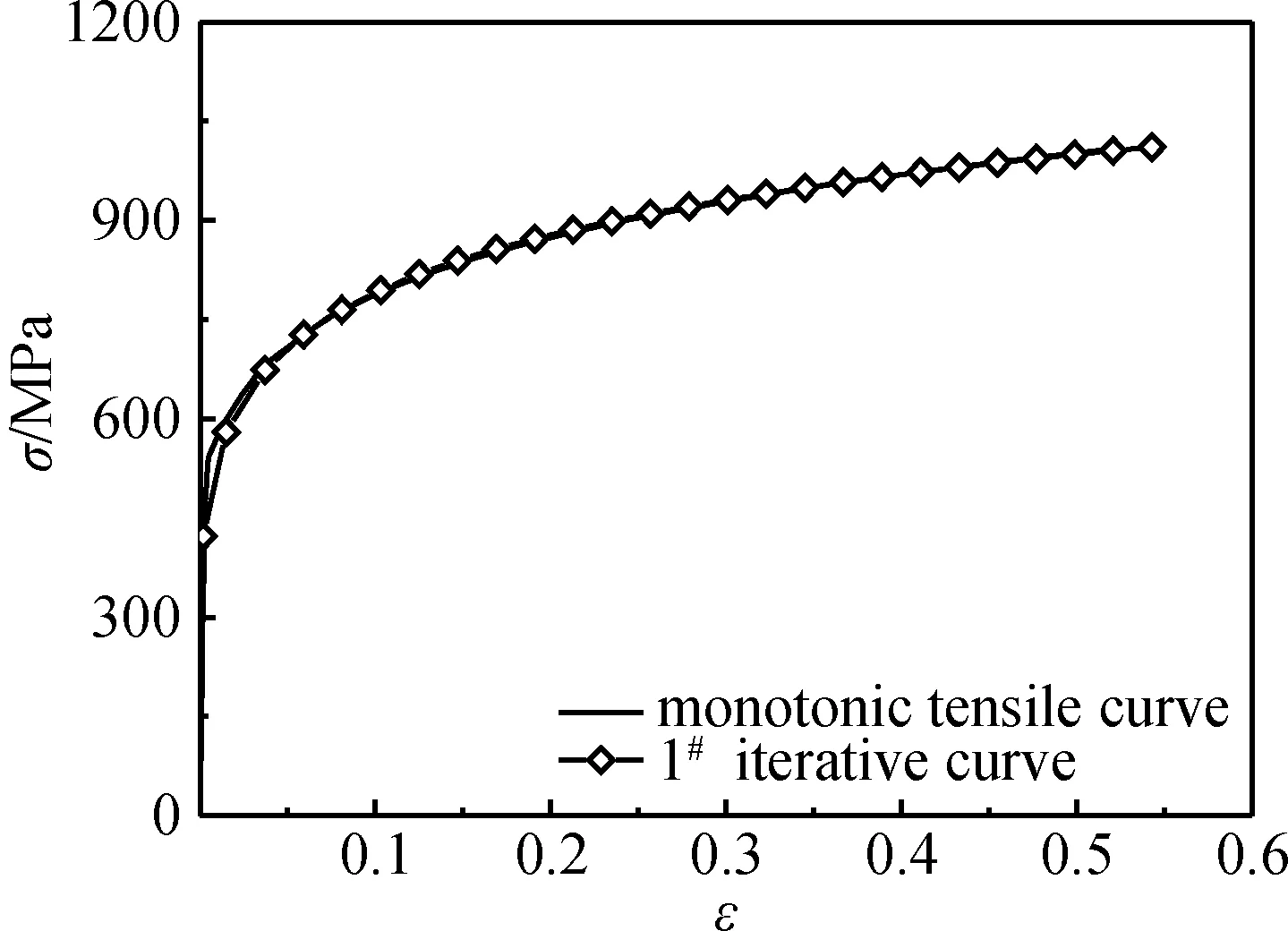
图13　迭代收敛时P92钢的单调拉伸的σ-ε曲线Fig.13　Comparison of experimental and uniaxial tensile curves for P92 steel

在运用FAT方法模拟计算缺口小试样的三点弯曲试验过程中，由图10和图11可以看出，迭代收敛时，1Cr12Mo钢1#的迭代PL-D曲线与实际试验曲线基本重合，且有限元计算的压头与试样接触点处的σ-ε曲线与单调拉伸本构关系曲线吻合良好。同样，1Cr12Mo钢2#，3#试样及P92钢1#(图12和图13)、2#，3#试样的迭代PL-D曲线与实际试验曲线也基本重合，计算的压头与试样接触点处的σ-ε曲线与单调拉伸本构关系曲线也吻合良好。从而体现了三点弯曲缺口小试样试验结果的可靠性和实用价值。最后，为了方便工程应用，给出了计算的Hollomon本构模型参数，如表5所示。

表5由FAT方法给出Hollomon本构模型参数

Table5ParametersofHollomonmodelgivenbyFATmethod

Parameter1Cr12MoP921#2#3#1#2#3#σy/MPa509495526507485503n0.1690.1790.1570.1520.1560.151

5　结论

(1)提出了基于FAT方法获取材料本构关系的力学性能测试新方法，该方法采用三点弯曲小尺寸缺口试样，其测试精度得到了验证。

(2)针对长度25mm的三点弯曲小尺寸缺口试样，应用FAT方法获得了材料Hollomon本构模型参数。

[1]READDT,DALLYJW.Anewmethodformeasuringtheconstitutivepropertiesofthinfilms[J].JMaterRes, 1992, 8: 1542-1549.

[2]TSUCHIYAT,TABATAO,SAKATAJ, et al.Specimensizeeffectontensilestrengthofsurface-micromachinedpolycrystallinesiliconthinfilms[J].JournalofMicroelectromechanicalSystems,1998, 7(1): 106-113.

[3]GREEKS,ERICSONF,JOHANSSONS, et al.Mechanicalcharacterizationofthickpolysiliconfilms:Young’smodulusandfracturestrengthevaluatedwithmicrostructures[J].JournalofMicromechanicsandMicroengineering, 1999, 9(3): 245.

[4]ESPINOSAHD,PROROKBC,PENGB.Plasticitysizeeffectsinfree-standingsubmicronpolycrystallineFCCfilmssubjectedtopuretension[J].JournaloftheMechanicsandPhysicsofSolids, 2004, 52(3): 667-689.

[5]CHASIOTISI,KNAUSSWG.InstrumentationRequirementsinmechanicaltestingofMEMSmaterials[C]∥MicroscaleSystems:MechanicsandMeasurementsSymposium,SocietyforExperimentalMechanics. 2000: 56-61.

[6]LAVANDA,BUCHEITTE,KOTULAPG.MechanicalandMicrostructuralCharacterizationofCriticalFeaturesofMEMSMaterials[C]∥MicroscaleSystems:MechanicsandMeasurementsSymposium. 2000: 41-45.

[7]JIANNINGD.Magnet-coilforceactuatorformicrotensiletestdevice[J].ChineseJournalofScientificInstrument, 2000, 21(5): 441-445.

[8]WUH,MENGYG,SUCJ, et al.Anppparatusformeasuringmechanicalpropertiesofmicrostructuresintensilemode[J].ScienceinChinaSer:GPhysics,MechanicsandAstronomy, 2004, 47:127-132

[9]OLIVERWC,PHARRGM.Animprovedtechniquefordetermininghardnessandelasticmodulususingloadanddisplacementsensingindentationexperiments[J].Journalofmaterialsresearch, 1992, 7(6): 1564-1583.

[10]BEAMSJW.Mechanicalpropertiesofthinfilmsofgoldandsilver[J].Structureandpropertiesofthinfilms, 1959: 183-192.

[11]WEIHSTP,HONGS,BRAVMANJC, et al.Mechanicaldeflectionofcantilevermicrobeams:Anewtechniquefortestingthemechanicalpropertiesofthinfilms[J].JournalofMaterialsResearch, 1988, 3(05): 931-942.

[12]OSTERBERGPM,SENTURIASD.M-TEST:atestchipforMEMSmaterialpropertymeasurementusingelectrostaticallyactuatedteststructures[J].JournalofMicroelectromechanicalSystems,1997, 6(2): 107-118.

[13]陈辉, 蔡力勋, 姚迪, 等. 基于小尺寸材料试验与有限元分析的耦合方法获取材料力学性能[J]. 机械强度, 2014, 36(2): 187-192.

(CHENH,CAILX,YAOD, et al.ObtainingMaterialMechanicalPropertiesbyCouplingMethodBasedonTestsofSmallSizeSpecimensAndFiniteElementAnalysis[J].JournalofMechanicalStrength, 2014, 36(2): 187-192.

[14]于思淼, 蔡力勋, 赵国明. 聚合物PA66 直至断裂的全程单轴本构关系研究[J]. 航空材料学报, 2015, 35(3): 60-68.

(YUSM,CAILX,ZHAOGM.Full-rangeuniaxialconstitutiverelationshipuptofailureofpolymerPA66[J].JournalofAeronauticalMaterials, 2015, 35(3): 60-68.)

[15]COLLINJM,MAUVOISING,PILVINP, et al.Useofsphericalindentationdatachangestomaterialscharacterizationbasedonanewmultiplecyclicloadingprotocol[J].MaterialsScienceandEngineering(A), 2008, 488(1): 608-622.

Obtaining Uniaxial Constitutive Relationships of Ductile Materials by Using Small-scale Notched Bending Specimens

YINTao，CAILixun，CHENHui，BAOChen

(AppliedMechanicsandStructureSafetyKeyLaboratoryofSichuanProvince,SchoolofMechanicsandEngineering,SouthwestJiaotongUniversity,Chengdu610031,China)

Atestmethodisproposedtoobtainuniaxialconstitutiverelationshipsofductilematerialsbyusingthesmall-scalebendingspecimenswithasemi-circlenotch.Linearload-displacementexperimentalcurvesofthespecimensunderthree-pointbendingtestsaretakenastheiterativereferencedtargetsothatRVE(Representativevolumeelement)uniaxialconstitutiverelationshipsoftheductilematerialsareobtainedbytheFAT(Finite-element-analysisaidedtests)method.Itisshownthattheuniaxialconstitutiverelationshipsfortwokindsofductilematerialsbyfinite-element-analysisareingoodagreementwiththestandardtensileresults.Therefore,themethodforthesmall-scalespecimenscanbeconvenientlyusedtogettheuniaxialconstitutiverelationshipsforductilematerials.

FATmethod；uniaxialconstitutiverelationship；small-scalespecimen;notchspecimen;threepointbendingspecimen

2015-07-18；

2015-11-06

国家自然科学基金资助项目(11472228)

蔡力勋(1959—)，男，教授，主要从事材料破坏与结构安全研究，(E-mail)lix_cai@263.net。

10.11868/j.issn.1005-5053.2016.1.014

TB302；O346

A

1005-5053(2016)01-0081-06