大尺寸缩比自由飞模型惯性矩测量与调整方法

王立波, 马坤, 杜欢, 王永超

(中航工业西安飞机设计研究所 总体气动设计研究所, 陕西 西安 710089)



大尺寸缩比自由飞模型惯性矩测量与调整方法

王立波, 马坤, 杜欢, 王永超

(中航工业西安飞机设计研究所 总体气动设计研究所, 陕西 西安 710089)

给出了双线摆法测大尺寸缩比自由飞试验模型惯性矩的方法和流程,并根据飞机类模型的惯性矩特点,提出了大尺寸缩比自由飞试验模型惯性矩调整所需的配重计算方法。双线摆法测量原理简单,不需要复杂的测量设备,具有较好的工程实用性。应用实例证明,模型飞机调整后的惯性矩与目标状态符合较好,测量精度满足工程应用要求。

惯性矩; 配重计算; 双线摆; 模型自由飞试验

0　引言

模型自由飞试验领域的科学研究与实践贯穿于飞机发展的百年长河,至今仍具有强大的生命力与发展价值。长期以来,国内外都曾通过丰富的模型自由飞试验对目标飞行器的气动布局、气动特性、操稳特性和飞行控制律开展探索、试验或验证,模型自由飞试验已成为有效支撑目标飞行器设计、化解技术风险、提高技术成熟度的飞行试验综合研究手段[1-3]。

近年来,小型动力装置、数据链路、自主飞行和遥控遥测设备性能的提升与发展,进一步促进了模型自由飞试验技术水平的大幅度提升。试验模型的系统更加精细和复杂,同时也使得模型的尺寸越来越大。

质量特性相似是缩比自由飞试验模型设计与制造的一项重要相似准则,即自由飞试验模型必须经过总装调配,使内部设备和配重合理分布,进而保证模型的质量、重心和惯性矩等质量特性参数与原准机保持相似关系[4]。目前,物体惯性矩的测量方法主要包括:

(1)双线摆法[5-6]。该方法比较适合测量外形复杂物体的惯性矩,其试验装置简单,对场地要求小,操作简便,计算公式简洁明了。

(2)三线摆法[7]。该方法比较适合测量外形简单的物体(如导弹模型)的惯性矩,其悬线较多,同时需要较为复杂的夹具与悬挂机构,对于飞机这类z向尺寸远小于x,y向尺寸的物体,用三线摆法不太方便。

(3)扭摆法[8]。该方法通常采用一套专用设备进行测量,与前两种方法相比,减少了中间传递量,可有效提高测量精度,但由于需要专用设备,待测物体的尺寸和质量均受仪器的空间和量程限制,同时专用设备系统复杂,购置、维护的成本较高。

对于大比例缩比验证机而言,一种快速、高效、经济的全机惯性矩测量和调整手段必不可少,是缩比模型自由飞试验顺利开展的重要保证。

1　理论基础

1.1双线摆法理论基础

如图1所示,在被测构件上选取A,B两点,用两根长度均为l的平行摆线AC,BD悬挂起来。摆线上端点C,D位于同一水平面内,且两平行摆线间距为2a。对构件施加水平力偶矩使构件绕其中心线偏离平衡位置后撤去外力,使构件做往复自由摆动构成双线摆,从而借助双线摆特性来测定被测构件的惯性矩。

图1　双线摆原理图Fig.1　Principles of the bifilar pendulum

已知被测构件的质量为m,重心G位于悬挂点A,B之间,与双线摆中心线的距离为lG。假设摆线的质量与被测构件相比可忽略不计,并忽略摆线的弹性和双线摆的阻尼,列写双线摆自由振动情况下的动力学方程。被测构件的运动可看作是构件绕双线摆中心线的刚体转动和沿双线摆中心线的刚体平动两种运动的复合。令构件偏转α角时,构件重心上升量为h,那么构件的动能E和势能V可分别表示为:

(1)

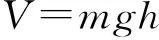
(2)

式中:I0为构件绕双线摆中心线的惯性矩。被测构件绕通过质心G与双线摆中心线平行的转轴的惯性矩为:

(3)

根据图1所示几何关系,h=BE,有:

(4)

(5)

将式(4)和式(5)的结果代入式(1)和式(2),得到:

(6)

(7)

对于微角摆动,即摆角α很小,则有sinα≈α。代入式(6)和式(7),忽略其中的二次及二次以上的小量后得到:

(8)

(9)

由此得到系统的Lagrange函数为:

(10)

对于自由度α,满足Lagrange的运动方程为:

(11)

将式(10)结果代入式(11),得到双线摆微角振动的动力学平衡方程为:

(12)

(13)

显然,式(13)描述的是一种简谐振动,其振动周期为:

(14)

那么,被测构件绕双线摆中心线的惯性矩为:

(15)

根据式(3)可知,被测构件绕通过质心G与双线摆中心线平行的转轴的惯性矩为:

(16)

1.2大尺寸模型飞机的惯性矩测量方法

基于上述双线摆法理论基础,对缩比验证机相对机体坐标系的惯性矩进行测定。如图2所示,将模型通过卡具按双线摆方式吊挂,并通过调整摆线的位置,保证模型的机身轴线处于竖直位置。两根摆线相对于机身轴线对称布置,同时为满足长摆线的要求,应当使摆线长度与摆线间距满足l≥10a。使模型绕双摆线中心线自由摆动,记录20～25个周期的总时间,求出摆动的平均周期Tx,应用惯性矩计算公式,求得模型滚转惯性矩为:

(17)

图2　滚转惯性矩测定时双线摆布置图Fig.2　Layout of bifilar pendulum for Ixxmeasuring

同理,将模型按图3和图4方式吊挂,即可分别测算得到模型的俯仰惯性矩和偏航惯性矩如下:

(18)

(19)

图3　俯仰惯性矩测定时双线摆布置图Fig.3　Layout of bifilar pendulum for Iyymeasuring

图4　偏航惯性矩测定时双线摆布置图Fig.4　Layout of bifilar pendulum for Izzmeasuring

1.3大尺寸模型飞机的惯性矩调整方法

飞机通常由机身、机翼和尾翼几大部件组成,其在立轴方向的尺寸要远小于在纵轴和横轴方向的尺寸。因此,一架飞机惯性矩分布一般满足以下关系式:

(20)

利用上述关系式,可使缩比自由飞模型调整全机惯性矩时的配重方案计算过程大大简化,具体配重方案如图5所示。

图5　用于惯性矩调整的配重方案示意图Fig.5　Layout of counterweight for moment of inertia adjustment

令左右翼尖处的配重质量为m1,沿机身轴线从前到后的配重质量分别为m2,m3和m4。已知配重前模型的质量和惯性矩分别为m0,Ixx0,Iyy0和Izz0,配重后模型的质量和惯性矩分别为m,Ixx,Iyy和Izz。在图5所示的坐标轴系下,各配重物相对目标重心的坐标位置差分别为(xi,yi,zi)。各配重物的位置一经确定,配重方案中仅含4个未知数,即各配重质量的大小。

以配重后全机总重、重心纵向位置,以及全机滚转惯矩和偏航惯矩作为约束条件,同时认为配重前后的重心位置不变,且各配重物绕各自重心的转动惯性矩相对于全机惯性矩可以忽略,列出平衡方程如下:

(21)

将上式整理成矩阵形式得到:

(22)

其中:

A=

通过求解代数方程组,即可得到各配重物的质量:

(23)

2　应用实例

某飞机带动力缩比验证机翼展4m,缩尺比例为1:7,采用两台电机驱动螺旋桨作为动力,用于气动布局可行性探索研究和低速操稳特性试飞验证。

缩比验证机制造和装配工序完成后,按照缩比模型自由飞试验要求,在飞行试验开始前需对该缩比验证机的质量、重心及惯量特性进行测量和调整,使得缩比模型与原准机之间满足质量特性相似要求。

某飞机及其缩比验证机质量/惯量目标状态具体参数如表1所示,两者重心位置均位于34%MAC处。

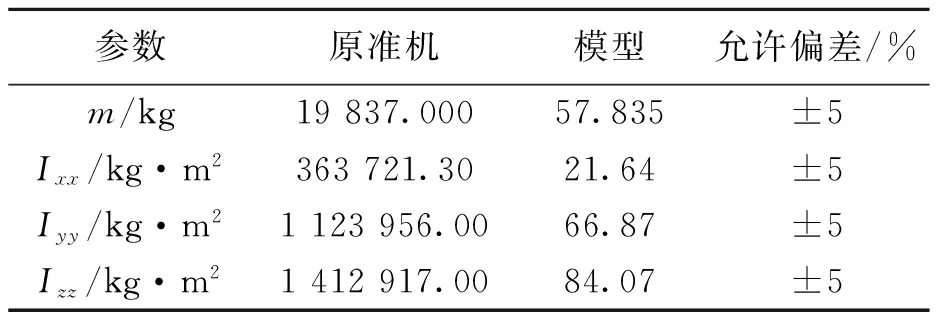
表1　某飞机与缩比模型质量/惯量目标状态Table1　Requirementsformasscharacteristicsadjustmentofthetestmodel

利用双线摆方法测算得到缩比验证机的初始惯性矩分别为Ixx=11.63 kg·m2,Iyy=37.18 kg·m2,Izz=46.21 kg·m2。选定4个配重点,计算得到的各配重点的质量如表2所示。

表2　缩比模型配重方案Table2　Counterweightdistributionofthetestmodel

表3给出了配重后模型的质量和惯性矩实测值与计算值的对比。结果显示采用双线摆法得到的惯性矩测量结果与计算结果符合良好,其测量精度满足工程应用要求。

表3　配重后模型惯量的实测值与计算值对比Table3　Comparisonofmassandinertiamomentmeasurementofcounterweightedtestmodelwithcalculationresults

表4给出了配重后模型的质量和惯性矩实测值与目标值的对比情况。结果显示采用本文的惯性矩调整方法得到的模型,其惯性矩与目标惯性矩精度均可控制在2%以内,同样满足工程应用的要求。

表4　配重后模型惯量的实测值与目标值对比Table4　Comparisonofmassandinertiamomentmeasurementofcounterweightedtestmodelwithdesignrequirements

需要说明的是,本次试验未将俯仰惯性矩作为约束条件,因此俯仰惯性矩的实测值与目标值之间的误差相对较大。在实际应用中,可视情况引入俯仰惯性矩目标值作为约束条件,只需在重心附近的机身轴线处增加一个配重点,使得方程组(22)满秩即可。

3　结束语

本文给出了采用双线摆法测量大尺寸缩比自由飞试验模型惯性矩的方法和流程。根据飞机类模型

的惯性矩特点,提出了一种大尺寸缩比自由飞试验模型惯性矩调整所需的配重计算方法。应用实例证明,模型飞机调整后的惯性矩值与目标状态符合较好,其测量精度满足工程应用要求,并且该方法不需要复杂的测量设备,具有较好的工程操作性。本文只给出了单个质量构型的配重方案计算实例,多个质量构型的配重方案优化以及对缩比自由飞模型初始构型惯量的设计要求还有待进一步的整理和研究。

[1]刘尚民,赵磊.电传飞机模型自由飞试验飞行控制技术研究[J].飞行力学,2012,30(1):83-86.

[2]Risch T,Cosentino G,Regan C D.X-48B flight-test progress overview [R].AIAA-2009-934,2009.

[3]Ratnayake N A,Koshimotoy E T,Taylorz B R.Multi-axis identifiability using single-surface parameter estimation maneuvers on the X-48B blended wing body [R].AIAA-2011-6273,2011.

[4]中国人民解放军总装备部军事训练教材编辑工作委员会.模型自由飞试验[M].北京:国防工业出版社,2001:233-251.

[5]黎肄彪.自由飞试验模型惯性矩的测定[J].流体力学实验与测量,2002,16(2):88-91.

[6]吴秀芳,柳涛.双线摆的周期及其测定[J].广西物理,1998,19(2):39-42.

[7]葛宇宏.长摆线三线摆大摆角摆动测定刚体转动惯量[J].机械科学与技术,2010,29(6):792-796.

[8]唐文彦,李慧鹏,张春富.扭摆法测量飞行体转动惯量[J].南京理工大学学报(自然科学版),2008,32(1):69-72.

(编辑：崔立峰)

A mass moment of inertia measuring and adjustment method for free-flight models

WANG Li-bo, MA Kun, DU Huan, WANG Yong-chao

(General Configuration and Aerodynamic Design Institute, AVIC Xi’an Aircraft Design Institute,Xi’an 710089, China)

Based on the theory of bifilar pendulum, a method for measuring the mass moment of inertia of the free-flight models was proposed in this paper, especially for the scaled demonstrators with large sizes. The counterweight calculation procedure for the mass moment of inertia adjustment was also established, where the characteristics of the mass moment of inertia distribution of the aircraft was adopted. The advantage of the bifilar pendulum method includes: simple measuring principle, easy operation, and neither expensive nor complicated device needed during the measuring progress. The application example indicates that the experiment result coincides well with the target value of the mass moment of inertia, which confirms that the method proposed in this paper is suitable for engineering application.

moment of inertia; counterweight calculation; bifilar pendulum; model free-flight test

2016-02-04;

2016-03-28; 网络出版时间:2016-03-29 15:37

王立波(1985-)，男，浙江上虞人，工程师，博士，研究方向为飞机气动布局设计与缩比模型自由飞试验技术。

V216.7; V217.4

A

1002-0853(2016)04-0077-04