可重复使用运载器连续推力轨迹回转机动方法研究

乔浩, 李新国

(西北工业大学 航天学院, 陕西 西安 710072)



可重复使用运载器连续推力轨迹回转机动方法研究

乔浩, 李新国

(西北工业大学 航天学院, 陕西 西安 710072)

针对可重复使用运载器(RLV)原场返回过程中所面临的轨迹回转问题,提出了一种在亚轨道高度进行姿态调整并使飞行轨迹回转、指向发射场方向的机动方法。在RLV与上面级分离之后,利用RLV自身推力抵消背离发射场速度,最终使RLV飞行方向指向发射场并进入再入返回阶段。采用连续推力方案,利用最优控制理论推导得出满足轨迹回转终端要求的机动指令。仿真结果表明,该方法能够实现RLV与上面级分离后轨迹迅速回转,可为之后的返回原发射场提供保障。

可重复使用运载器; 原场返回; 轨迹回转

0　引言

可重复使用是未来航天运载器的一大特征,在节约成本等方面具有传统一次性运载器无可比拟的优势。可重复使用运载器(Reusable Launch Vehicle,RLV)作为这类运载器的代表,一般采用垂直发射、水平着陆的方式[1-2]。根据返回时对应着陆场的位置,可分为沿发射方向异场返回和轨迹回转(Return to Launch Site,RTLS)两大类。前者指RLV与上面级载荷分离之后,不改变飞行方向,经过分离后上升段、再入段对准着陆场并水平着陆;后者指RLV与上面级分离后,经过一系列机动实现速度反向,之后再入返回原发射场。

现有再入研究一般集中在前一种返回方式,此时RLV飞行较为平稳,无大机动转向,再入返回过程相关技术亦较为成熟。但该方法要求沿航向设置着陆场,大大增加了系统规模,增加了人力、物力的投入,与降低成本的目的相悖。与之相比,RTLS方式下整套运载系统围绕同一个发射场展开,系统规模与运作成本均大幅减少,并可缩短两次发射间的准备时间,具有一定的商业化、规模化前景[3]。

早期RTLS模式一直被作为航天飞机应急返回的一种备用方案[4],并未作为一种新型返回方案,直到21世纪初,这方面的研究才逐渐兴起。美国空间系统设计实验室(Space System Design Lab)在2005年发表的一份针对AE8900 MS特别问题报告中详细讨论了RTLS返回的研究意义及存在问题,并初步将返回方式分为无动力返回、火箭动力返回和航空动力返回三种[5];但未给出各种返回方式的具体实现方法,且研究对象分离高度较低,与RLV设计要求不符。日本东京大学在2003年对比了航空动力返回以及无动力返回两种方案[6],对比结果显示,要实现无动力返回,RLV与上面级之间的质量比须较小;而采用航空动力返回,运载器总质量会大大增加,运输成本增大。

相对而言,国内对RTLS问题的研究较少。文献[7]利用优化方法对RLV的原场返回问题进行了研究,分析了不同滚转角对三维飞行大回转能力的影响,得出在保证再入飞行条件的前提下,滚转角越大越能发挥RLV原场返回能力的结论。文献[8]对可重复使用助推器的原场返回问题进行了研究,但仍未给出机动过程的具体实现方法。

在不考虑级间分离问题的前提下,连续推力是一种较简单的轨迹回转方式。该方案在高度、速度达到一定条件后释放上面级,之后发动机继续工作,使用剩余燃料进行俯仰机动并使RLV达到再入返回条件。本文即在此背景下采用连续推力,研究轨迹回转过程中的最优俯仰机动方法。

1　问题描述

RLV一般作为可重复使用运载系统的下面级,将上面级运送至约60km高度并达到一定速度,之后与之分离。当不改变分离后RLV飞行速度方向时,RLV再入返回形式与现有再入返回相同。由于原场返回具有现有再入返回无可比拟的优势,因此具有较高的研究价值。原场返回所面临的首要问题即飞行轨迹的回转。在连续推力作用下,整个过程的机动主要表现为俯仰机动,因此俯仰指令的优劣决定了轨迹回转的效果。

由于自分离点到轨迹回转终点RLV飞行持续时间较短,飞行轨迹基本处于发射平面内,因此可在平面地球假设下建立该过程动力学方程:

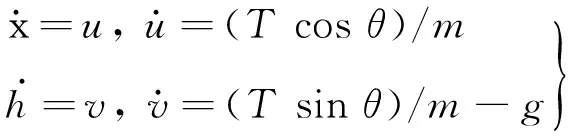
(1)

式中:x为纵程;h为高度;u为速度水平分量;v为速度垂直分量;T为发动机推力;g为重力加速度。由于整个机动过程在分离点之后,即60 km以上,因此上式中忽略气动力影响;T取真空推力Tvac。为简化分析,假定推力方向与飞行器纵轴方向一致,此时θ即俯仰角,其与航迹倾斜角γ及推力迎角α存在如下关系:

(2)

机动过程开始于两级分离点,结束于达到一定的终端条件,整个过程受到燃料量、推力大小等因素的影响,因此可将该问题转化为一个最优控制问题来研究。RLV与上面级分离的初始条件为:

(3)

若要求在机动结束即关机点处耗尽所剩燃料,且秒流量为常值,则在燃料有限情况下该过程属于终端时间固定问题。由于轨迹回转终端一般限制为飞行总速度V或航迹倾斜角γ,而二者有:

(4)

因此其性能指标可统一表示为:

(5)

假定终端约束形式为:

(6)

当要求终端航迹倾斜角满足γf=Γf,Γf>π/2为给定终端航迹倾角,此时终端约束可采用:

(7)

该最优控制问题有最优解的条件为首先需保证梯度向量∂gf/∂vf≠0。由此整个过程转化为在满足动力学方程、初始条件、终端约束情况下,寻求俯仰角θ使性能指标最小的最优控制问题。

2　最优俯仰角指令推导

该最优控制问题的哈密尔顿函数为:

(8)

式中:AT为推力加速度。由于状态方程、性能指标及终端约束与h,x无关,此时有:

(9)

即λu与λv为常值。令λu=C1,λv=C2,由最优性必要条件可得最优俯仰角θc满足:

(10)

可得θc为常量。即整个机动过程中,θc应为一个特定值,RLV从初始俯仰角快速过渡并保持到θc,之后姿态不再进行调整,RLV在发动机推力作用下实现飞行轨迹的回转。

横截条件为:

(11)

式中:λ为拉格朗日乘子。由于∂gf/∂vf≠0,在已知θc情况下,横截条件必有解。因此,该最优控制问题转化为单参数搜索问题,即寻求常值控制量θc使之满足终端约束。

推力加速度为:

(12)

(13)

其中:

3　不同俯仰角指令下轨迹回转仿真

由上述分析可知,整个轨迹回转最优控制的最优俯仰角指令θc为常值。因此整个机动过程转化为根据不同设计要求搜索这一恰当常值的问题。由于从当前俯仰角θ过渡到θc需要经过必要的姿态机动,考虑实际情况,设计θ的一阶过渡过程为:

(14)

式中:τ为时间常数,表征由当前俯仰角过渡到所需俯仰角的角速率大小,本文取τ=1 s。对于不同θc,θ的过渡过程如图1所示。

由图1可以看出,θ需经过一定时间达到最优俯仰角指令,其过渡过程表现为初始角速率较大,到达θc附近逐渐减小,并最终稳定于θc。以某型RLV为研究对象,轨迹回转段初始俯仰角θ0=30°,初始航迹倾角γ0=25°,限定分离后发动机可继续工作80 s,采用不同俯仰角指令θc所得轨迹回转效果如图2和图3所示。

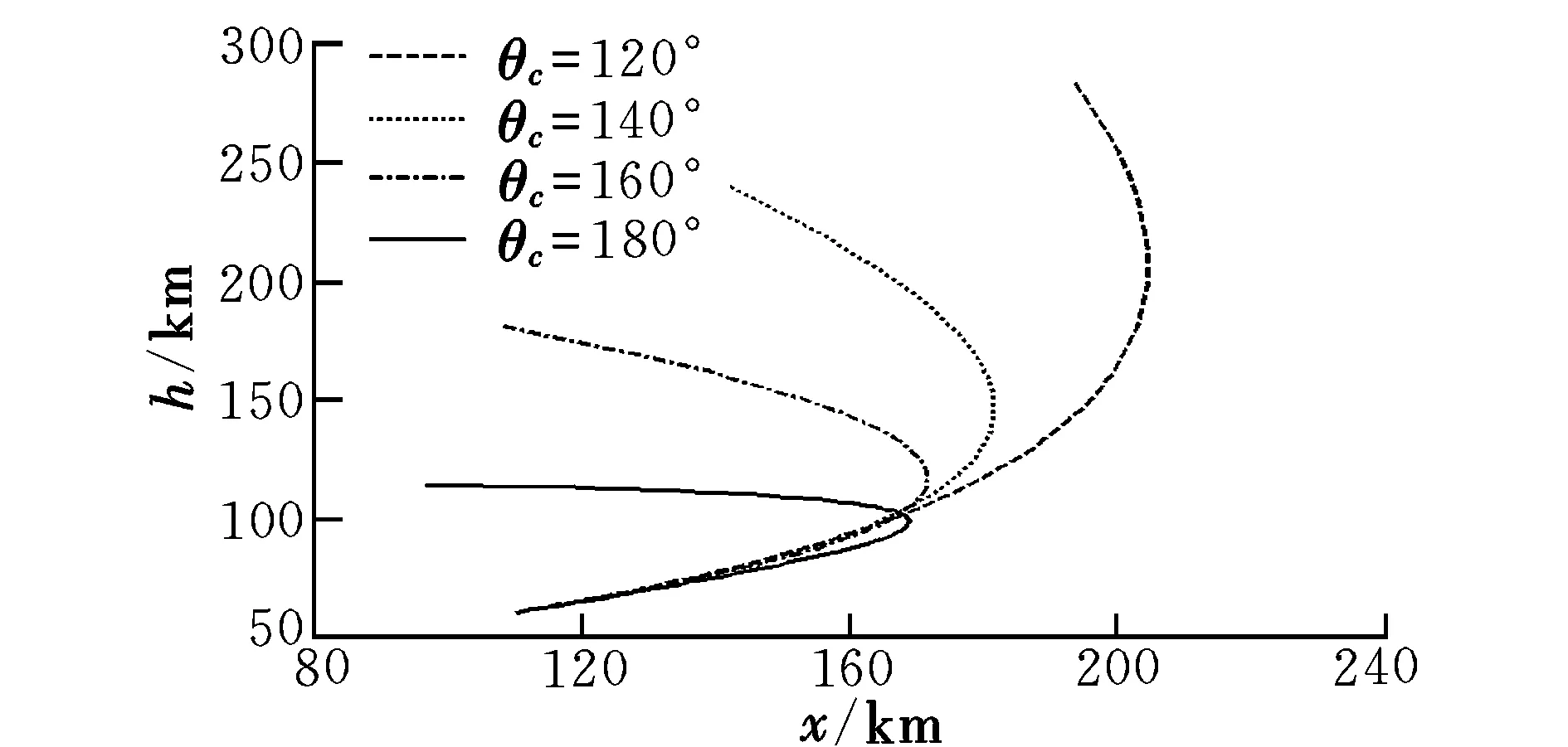
图2　轨迹回转段飞行轨迹Fig.2　Flight path in trajectory rotation phase

图3　轨迹回转段航迹倾角Fig.3　Flight path angle in trajectory rotation phase

由图2和图3可以看出,较小的θc将导致轨迹高度迅速增加,而回转效果不明显;较大的θc条件下,轨迹回转迅速,终端航迹倾角接近180°,为后续再入返回提供了良好的初始条件。

由于在轨迹回转过程中,水平速度存在反向现象,因此可将水平速度是否“过0”作为轨迹是否已回转的判断依据,如图4所示。

图4　水平速度Fig.4　Level speed

可以看出,180°俯仰角指令条件下水平速度最先“过0”,且在燃料耗尽时所达到的反向水平速度最大,有利于后续再入。因此在飞行器结构强度允许的前提下,θc越大越利于轨迹回转。

4　考虑实际回转过程的θc实时指令推导

对于包含终端航迹倾角约束的俯仰机动问题,即寻找一个俯仰角指令θc使得终端航迹倾角γf=Γf。当限定整个俯仰机动持续时间,即tf已知时,可得:

(15)

则限定γf时对应的俯仰角指令θc为:

(16)

出于终端精度考虑,计算过程中在每个制导周期均根据当前状态重新生成最优俯仰指令θc。在t时刻,以当前速度u(t)和v(t)代替u0和v0,以剩余时间tleft=tf-t代替tf,代入式(16),得:

(17)

其中:

可见,实时俯仰指令θc与当前状态u(t),v(t)均有关。由于在计算过程中,当tleft=tf-t→0时,式(17)存在奇异;因此当tleft小于某一设定值tδ时,俯仰指令不再更新,采用前一个制导周期所得θc作为最后的俯仰角指令飞至关机点。再入返回初始轨迹水平指向发射场最佳,因此取γf=180°,tf=80 s,tδ=7 s,可得相应实时俯仰指令θc如图5所示,对应航迹倾角变化如图6所示。

由图5可知,轨迹回转段终端更新所得的θc指令为172°附近,此时推力迎角为负值,推力竖直分量与重力反向,使轨迹维持于水平状态。由图6可见,在θc制导指令下,γ由初始值逐渐过渡并稳定至180°。

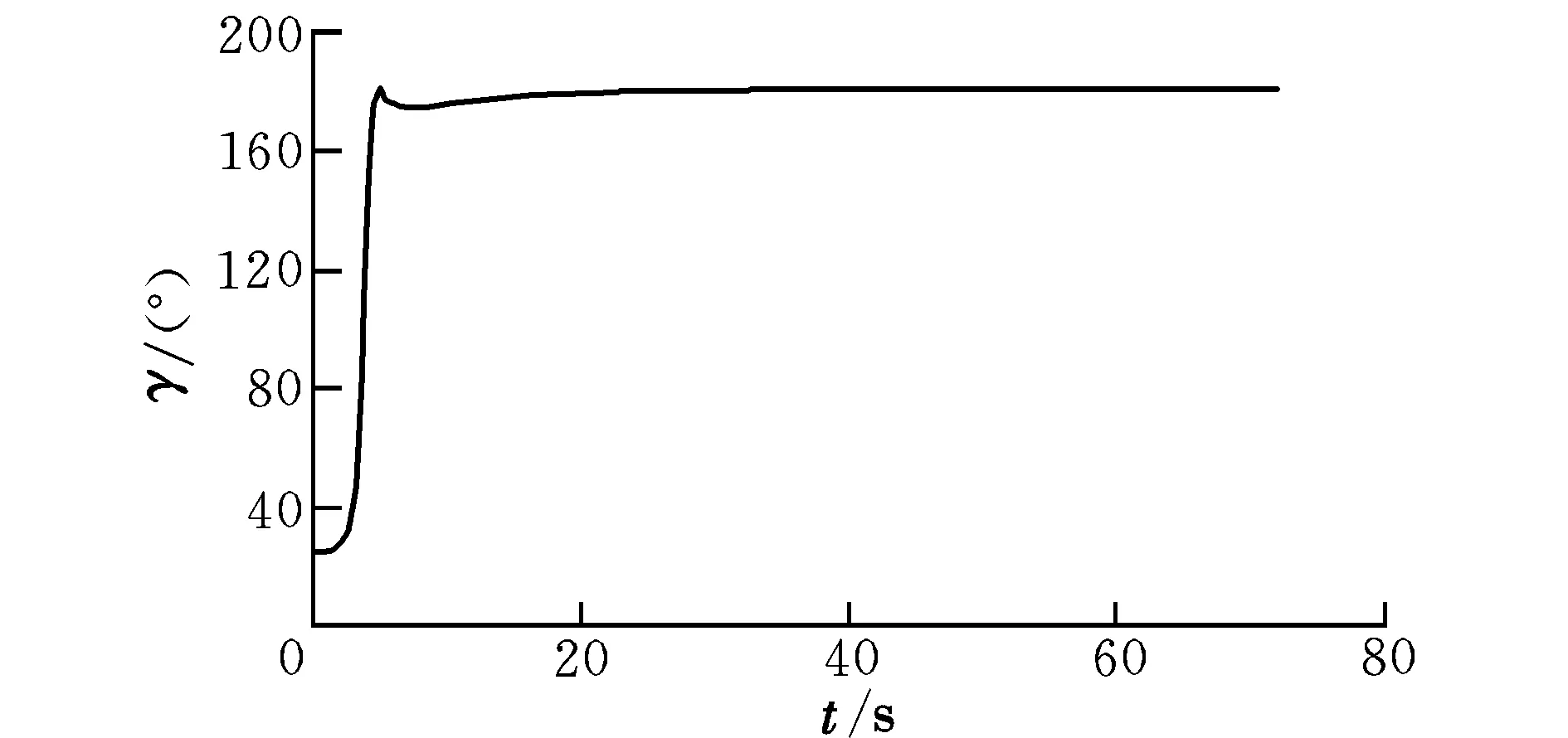
图6　带终端约束的航迹倾角变化曲线Fig.6　Variation of flight path angle with terminal restraint

综上所述,利用最优控制理论可设计出满足终端航迹倾角约束的最优俯仰机动指令。由于终端航迹倾角对再入返回过程具有较大影响,因此该设计方法对整个RTLS的实现具有重要意义。由于整个轨迹回转处于真空环境,因此指令搜索过程中无过多边界限制,指令搜索迅速,可满足在线制导要求。

5　结束语

本文基于最优控制理论推导了连续推力情况下轨迹回转的最优机动方式,得出最优俯仰角指令的设计方法,并针对终端航迹倾角限制的情况进行了深入讨论,设计出满足在线制导要求的最优俯仰角指令。仿真结果表明，该方法能够快速实现轨迹回转,并满足一定的再入返回条件。在解决RLV与上面级热分离以及姿态调整与轨迹调整的耦合关系后,该方法具有较高的实用性。

[1]王振国,罗世彬,吴建军.可重复使用运载器研究进展[M].北京:国防工业出版社,2004:12-56.

[2]杨勇,王小军,唐一华,等.重复使用运载器发展趋势及特点[J].导弹与航天运载技术,2002(5):15-19.

[3]Martin J C,Law G W.Suborbital reusable launch vehicles and applicable markets[R].Washington,D C:The Aerospace Corporation,2002.

[4]Baker D.NASA space shuttle:owners’ workshop manual (1981 onwards all models) [M].Bristol:Haynes Press,2011:21-30.

[5]Hellman B M.Comparison of return to launch site options for a reusable booster stage [R].Atlanta:AE8900 MS Special Problems Report,2005.

[6]Iwata T,Sawada K,Kamijo K.Conceptual study of rocket powered TSTO with fly-back booster [R].AIAA-2003-4813,2003.

[7]王志刚,袁建平,陈士橹.高超声速航天器最优再入大回转轨迹与控制[J].弹道学报,2005,17(2):60-64.

[8]韩鹏鑫.可重复使用助推器的导航、制导与控制方法研究[D].哈尔滨:哈尔滨工业大学,2011.

(编辑：李怡)

Trajectory rotation method for RLV with continuous thrust

QIAO Hao, LI Xin-guo

(School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

For the trajectory rotation problem of RLV during returning to launch site, a method to adjust attitude and return to launch site in suborbital altitude. After the RLV depart from the upper stage, the initial speed is canceled by its thrust. The RLV reverses towards the launch site and starts the re-entry phase. Using the continuous thrust scheme, the pitching angle guidance instruction was derived based on the optimal control theory. Simulation results show that this method can make the trajectory rotation quickly and provide support for the re-entry phase.

reusable launch vehicle; return to launch site; trajectory rotation

2015-09-18;

2015-12-14; 网络出版时间:2016-02-29 16:37

乔浩(1989-)，男，陕西渭南人，博士研究生，研究方向为飞行器制导与控制、飞行器系统仿真；

李新国(1966-)，男，湖南常德人，教授，博士生导师，研究方向为飞行器系统工程与仿真、空天飞行系统与技术。

V448.2

A

1002-0853(2016)04-0069-04