改进的双约束稳健Capon波束形成算法
2016-08-30李立欣白童童张会生申礼斌西北工业大学电子信息学院西安710129
李立欣 白童童 张会生 包 涛 申礼斌(西北工业大学电子信息学院西安710129)
改进的双约束稳健Capon波束形成算法
李立欣*白童童张会生包涛申礼斌
(西北工业大学电子信息学院西安710129)
传统双约束稳健Capon波束形成算法采用牛顿迭代法求解最优加载量,存在计算精度低且运算量大的问题。该文提出一种改进的双约束稳健Capon波束形成(DCRCB)算法,该算法对信号协方差矩阵进行重构,基于期望信号导向矢量在噪声子空间的投影最优,将重构后的干扰加噪声协方差矩阵投影到噪声子空间,得到基于噪声子空间的双约束算法模型。该算法中通过模约束的辅助约束作用,将改进的双约束算法模型转化为单约束问题,最终解得最优对角加载量的解析表达式。仿真结果表明改进算法能通过调整主瓣宽度优化波束旁瓣,有效提高了抗矢量偏差的鲁棒性,同时降低了运算量。
自适应波束形成;双约束Capon波束形成;信号协方差矩阵重构;噪声子空间
1 引言
波束形成是阵列信号处理的一项重要技术,广泛应用于无线通信、声呐、雷达和麦克风语音阵列处理等领域[14]-。然而,在实际工程应用中,当基阵位置的偏差较大、各阵元通道幅度和相位响应不一致、阵型失配时,算法性能会受到严重影响[57]-。因此,如何有效改善自适应波束形成的稳健性具有重要意义。
文献[8~10]提出了一类有严格理论基础的基于导向矢量不确定集的稳健Capon波束形成算法,在此基础上,近年来出现了许多新的改进的稳健Capon波束形成算法[1115]-。其中文献[10]提出了强加导向矢量不确定集和模值约束以改善其稳健性,即双约束稳健Cpaon波束形成(Double Constraint Robust Capon Beam former,DCRCB)算法,该算法属于对角加载算法的一种,可以根据不同的导向矢量误差得到合适的加载量。其最优对角加载量通过牛顿迭代法求解,但是迭代的运算量一般比较大而且收敛速度慢。文献[15]提出一种新的基于导向矢量不确定集的稳健Capon波束形成算法,并且利用特征向量的结构特性推导出了最优对角加载量的解析表达式,但是基于单约束的Capon波束形成算法鲁棒性不高,无法使所提算法的性能达到最优。本文基于期望信号导向矢量在噪声子空间的投影最优,并对信号协方差矩阵进行重构,提出一种改进的双约束稳健Capon波束形成算法。通过分析求解不确定集约束下的Capon波束形成算法可知,不确定集约束决定该算法的性能,导向矢量的模约束只起辅助约束作用,因此可以去掉改进的双约束稳健Capon波束形成算法模型中的模约束,将算法模型转化为单约束问题,求解单约束问题的最优对角加载量,然后对其进行标量化。该算法运算量低于迭代求解的方法,提高了加载量的计算精度,并且因为进行了信号协方差矩阵重构,算法的鲁棒性提高,旁瓣增益大大降低。
2 双约束波束形成算法及其求解
考虑阵列是由M个阵元组成的理想均匀线阵,远场空间存在一个目标信号和互不相关的P个干扰信号。则第k次快拍阵列的接收数据矢量可以表示为
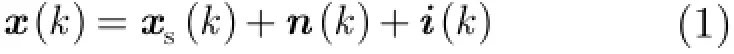
对接收数据进行波束形成,则波束形成器的输出为

根据阵列信号模型,双约束波束形成算法的优化模型可以描述为
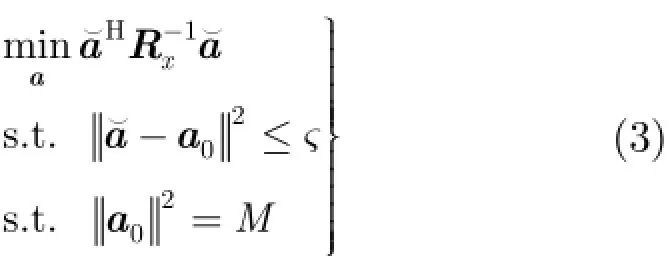
利用Lagrange因子方法求解式(3),可以得出方向向量的估计值。需最小化目标函数为
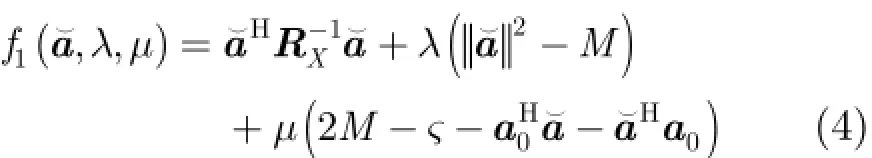
式中,,λμ为实数的Lagrange因子,对式(4)求解可得出方向向量的估计值。
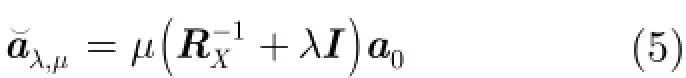
将方向向量代入,可得
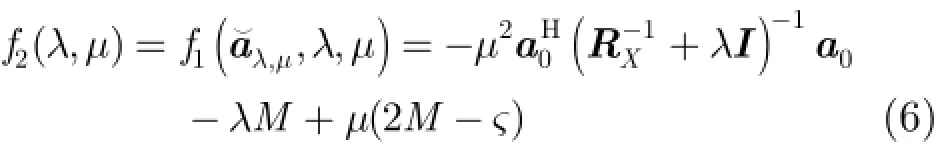
将式(6)对μ求导并令其等于零,可得

将μ代入式(6),可得
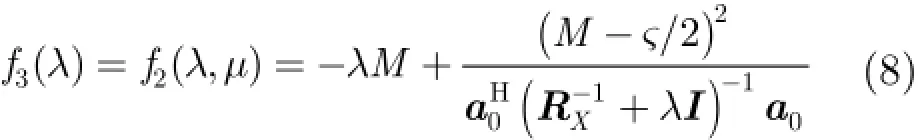
Lagrange因子λ可以通过式(9)求得
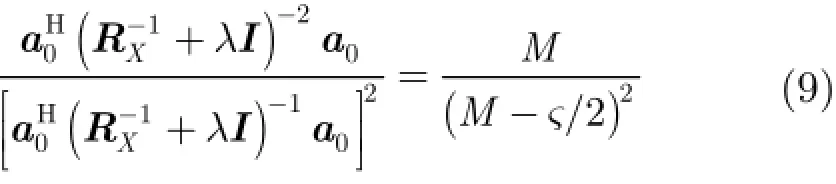
把式(7)代入式(5),可得信号方向向量的估计值为
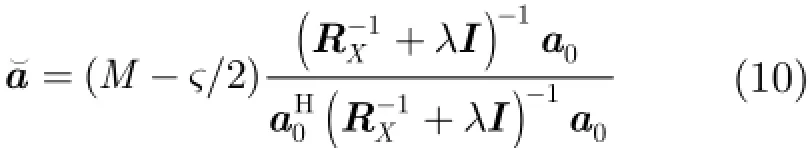
又解得λ的取值范围为
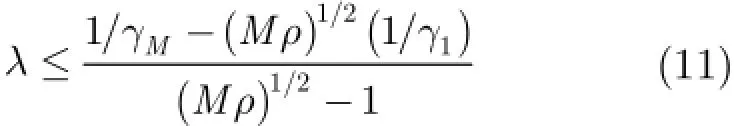
利用牛顿法解式(9)求出中满足式(11)的拉格朗日因子λ,将λ代入式(7)得到μ,进而求解式(5),得出方向向量的估计值。从而得到权重向量公式为

由于双约束波束形成算法没有对信号协方差矩阵进行重构,所以在抑制干扰信号的同时也抑制了期望信号,导致对干扰信号零陷不够深。并且此算法对角加载值通过牛顿迭代法求得,计算量较大。因此,提出改进的双约束波束形成算法对上述问题进行改进,提高算法性能。
3 改进的双约束波束形成算法及其求解
3.1改进的双约束波束形成算法
目前,有很多对信号协方差矩阵进行重构的方法,比如利用窗函数进行重构[16],构造平均协方差矩阵[17],重新定义一个谱来构造干扰加噪声协方差矩阵[18],空间功率谱估计[19]等。前面3种方法侧重于对干扰零陷的展宽,并且在展宽零陷的同时使得零陷深度变浅,因为本文的研究重点在于滤除协方差矩阵中的期望信号,加深零陷深度,提高算法抗导向矢量偏差的鲁棒性,而且利用空间谱估计来重构信号协方差矩阵这种方法的复杂度较低,并且性能良好,在多篇论文中也已经得到验证,综合考虑后,故采用空间功率谱估计的方法来重构信号协方差矩阵。
下面针对导向矢量失配问题,对信号协方差矩阵进行重构
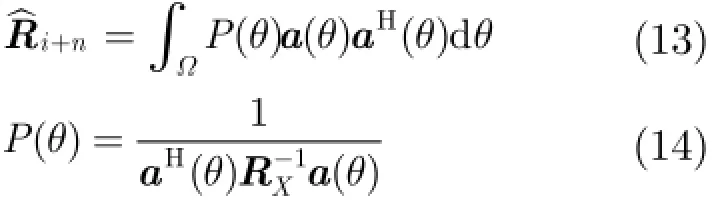
式中,()Pθ为空间谱函数,式(13)中ˆin+R是重构的干扰加噪声协方差矩阵,Ω为定义的干扰区间,实际应用中,对Ω的选择没有特别严格的要求,只需保证所有干扰分量均包含于Ω内,而期望分量不在Ω内即可。假设θ代表期望信号区间,满足θΩ∩=ø,θΩ∪为整个观测区间。基于此方法,调整Ω和θ的大小可获得不同的波束响应特性。例如,增加θ减小Ω会使主瓣变宽,导致波束分辨率降低,但能获得更低的旁瓣级;减小θ增大Ω则会有相反的效果。实际应用中,Ω和θ的大小根据需求设定。
将式(14)代入式(13)可得
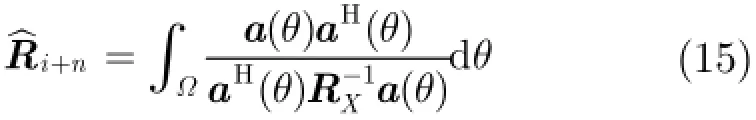
式(15)为重构后的干扰加噪声协方差矩阵。
在仿真中,我们采用的是求和的方法来对此式进行求解,将干扰区间Ω分为L个方向,每一个方向的导向矢量为进行L次积分求和,公式为
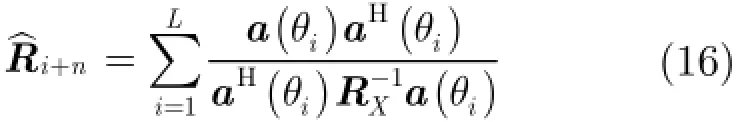
用重构后的协方差矩阵ˆin+R代替式(3)中的那么DCRCB算法可描述为
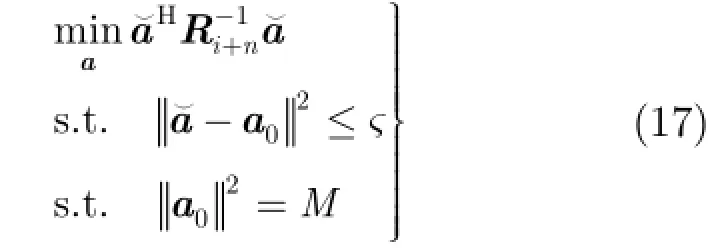
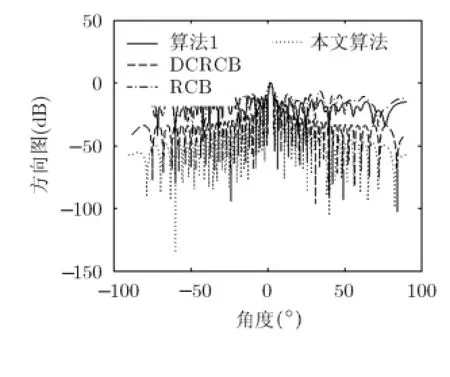
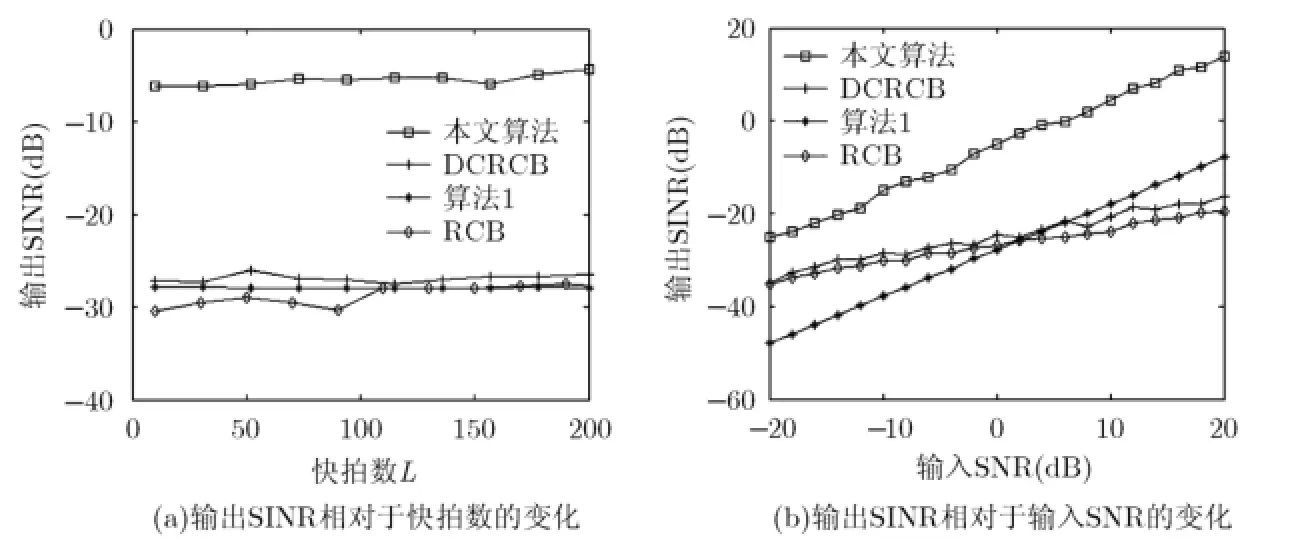
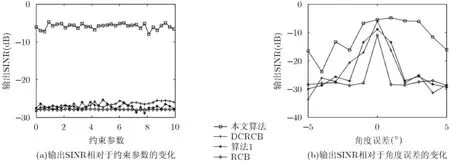
在进行分析之前,假定天线阵列接收端总共有P+1 式中,a表示组合系数组成的列向量。 把式(19)和式(18)代入式(17)中,可得 3.2改进的双约束波束形成算法的求解 通过分析求解双约束下的Capon波束形成算法,可以得到导向矢量的模约束只是起辅助约束的作用,这是因为对于满足不确定约束的解进行标量化,使其满足模约束,然后代入信号功率的估计式中,只是相当于增加了一常数因子。因此,对于式(22)的求解可以转化为求解单约束波束形成算法。 这样把式(23)中的不等式约束转化为等式约束。 式(25)的最优解是利用拉格朗日因子的方法最小化函数f: 这样,最优对角导向矢量的求解将依赖于λ值,为求解λ,将式(27)代入式(26)可得 将式(31)代入式(28)可得 解式(33),由于0λ≥,因而可以得到其解为 将式(34)代入式(27)就可得最优导向矢量的精确解,因此,本文提出的改进的双约束波束形成算法的求解步骤就能得到了。但是需要注意的是,本文算法需要准确知道噪声子空间的维数,因此需要估计信号源的数目,当信号和干扰功率较强时,可以直接从特征值的界限加以判断。但是当功率较弱时,无法直接判断,这时则可以通过信源估计方法[20]估计。算法的实现步骤如下: 步骤1对信号协方差矩阵进行重构,滤除协方差矩阵中的有用信号。 步骤2对重构后的干扰加噪声协方差矩阵进行特征值分解,求出噪声子空间的特征向量矩阵。 步骤3根据NU求z,得到z后,把选定的约束参数ς代入到式(34)很容易求得最优λ,将λ代入式(27),得到最优对角加载量,对进行标量化,使其满足如令即得满足双约束的最优解。 步骤4计算最优权矢量 为了验证算法的正确性,进行如下的仿真实验。考虑阵列阵元数为50,阵元间隔为半个信号波长的理想均匀线阵。本文假设信源的数目已知,且信号互不相关。假设空间存在一个有用信号和2个互不相关的干扰信号,其中假定期望信号来波方向为0o,实际来波方向为2o。信噪比为0 dB。两个干扰信号功率分别为40 dB,50 dB,相应的干扰信号方向为-60o,40o。 为了验证本文算法的稳健性,图1给出了几种Capon波束形成算法方向图。其中RCB算法和DCRCB算法分别为文献[8]提出的稳健Capon波束形成算法和文献[10]提出的双约束稳健Capon波束形成算法,算法1表示文献[15]提出的新的稳健Capon波束形成算法。算法的参数ς根据经验选择为3.2。 从图1可以看出,本文算法能够准确地指向信号真实的期望方向,并且具有较低的旁瓣,而且在两个干扰方向均能形成零陷。因为对信号协方差矩阵进行了重构,将期望信号滤除,因此能提高算法的鲁棒性。并且因为本文算法使期望信号导向矢量在噪声子空间的投影最优,因此算法的旁瓣较低。DCRCB算法虽然也具有较低的旁瓣,且在干扰方向形成零陷,但是在期望信号方向也能形成零陷。RCB算法和算法1旁瓣增益太大,效果较差。 图2(a)给出了不同快拍数对波束形成器输出SINR的影响。显然本文提出的新的双约束鲁棒波束形成算法输出SINR性能明显高于其他3种算法,这是因为新算法旁瓣较低。DCRCB算法性能优于RCB算法和算法1,并且算法的输出性能随着快拍数的增大逐渐趋于平稳,RCB算法和算法1在快拍数较大时性能比较接近。 图2(b)给出了几种算法的不同输入SNR的变化对输出SINR的影响。可以看出随着输入SNR的增大,4种算法的输出SINR都在逐渐增大,并且本文算法与算法1的曲线斜率基本一致,DCRCB算法与RCB算法曲线斜率基本一致,这是由算法的最优对角加载量的求解方式决定的。由图2可知,本文算法在输入SNR相同时输出SINR至少比其他算法大10 dB,并且随着输入SNR的增大,该算法的优势体现的越来越大。算法1在SNR较大时性能优于DCRCB和RCB两种算法。 图3(a)给出了不同约束参数对输出SINR的影响。4种算法的输出SINR受约束参数的影响都不大,因为本文算法对信号协方差矩阵进行重构且期望信号导向矢量在噪声子空间投影最优,所以其旁瓣低,主瓣宽,因此其输出SINR性能明显高于其他3种算法,且约束参数为3到7之间时输出性能比较稳定。其他3种算法的输出性能受约束参数的影响差别不大。 图3(b)给出了不同角度误差对输出SINR的影响。本文提出的新的双约束鲁棒波束形成算法输出SINR性能明显高于其他3种算法,这是因为该算法在对信号协方差矩阵进行重构时,合理选择积分范围能够使得方向图主瓣变宽,旁瓣降低,使得算法在角度误差较大时仍能保持较好的性能。RCB和DCRCB算法抗角度误差性能较差,算法1较两种算法抗角度误差性能有了一定提升,但是当角度误差大于1o时,性能下降比较严重。 图1 Capon波束形成算法的方向图 图2 输出SINR相对于不同参量的变化 图3 输出SINR相对于不同参量的变化 基于双约束稳健Capon波束形成算法,本文提出一种新的双约束稳健Capon波束形成算法。该算法基于期望信号导向矢量在噪声子空间的投影最优,并对干扰协方差矩阵进行重构,给出了该算法的最优对角加载量的解析表达式。理论分析和仿真实验表明,本文提出的新的DCRCB算法运算量小且旁瓣低于其他算法。不管在何种情况下,其输出性能均优于其他算法。 [1]李洪涛,陈斌,曾文浩,等.基于导向矢量估计的鲁棒自适应波束形成算法[J].电波科学学报,2015,30(1):188-194. LI Hongtao,CHEN Bin,ZENG Wenhao,et al.Steering vector estimation based robust adaptive beam form ing algorithm[J].Chinese Journal ofRadio Science,2015,30(1): 188-194. [2]金伟,贾维敏,姚敏立,等.一种分解迭代二阶锥规划鲁棒自适应波束形成算法[J].电子与信息学报,2012,34(9): 2051-2057.doi:10.3724/SP.J.1146.2012.00146. JIN W ei,JIA W eim in,YAO M inli,et al.An robust adaptive beam form ing algorithm using decom position and iterative second-order cone programm ing[J].Journal of E lectronics& Information Technology,2012,34(9):2051-2057.doi:10. 3724/SP.J.1146.2012.00146. [3]ZHAO H P,DAIY H,ZHU D Z,et al.Robust beam-space adaptive beam form ing algorithm[J].Application Research of Computers,2014,(4):1151-1153. [4]ROH W,SEOL J Y,PARK J,et al.M illimeter-wave beam form ing as an enabling technology for 5G cellular communications:theoretical feasibility and prototype results[J].IEEE Commun ications M agazine,2014,52(2):106-113. [5]李文兴,毛晓军,孙亚秀.一种新的波束形成零陷展宽算法[J].电子与信息学报,2014,36(12):2882-2888.doi:10.3724/SP.J. 1146.2013.02018. LI Wenxing,MAO Xiaojun,and SUN Yaxiu.A new algorithm for nu ll broadening beam form ing[J].Journal of Electronics&Information Technology,2014,36(12): 2882-2888.doi:10.3724/SP.J.1146.2013.02018. [6]XIA M,WU Y C,and AISSA S.Non-orthogonal opportunistic beam form ing:performance analysis and im plementation[J].IEEE Transactions on W ireless Comm un ications,2012,11(4):1424-1433. [7]HOU Yunshan,ZHANG Xincheng,and JIN Yong.Adaptive beam form ing algorithm based on interference-noise covariance matrix reconstruction[J].Journal of Computer Applications,2014,34(3):649-652.doi:10.11772/j.issn.1001-9081.2014.03.0649. [8]STOICA P,WANG Z,and LI J.Robust capon beam form ing[J].IEEE Signal Processing Letters,2002,1(6):172-175. [9]LI J,STOICA P,and WANG Z.On robust capon beam form ing and diagonal loading[J].IEEE Transactions on Signal Processing,2003,51(7):1702-1715. [10]LI J,STOICA P,and WANG Z.Doubly constrained robust capon beam former[J].IEEE Transactions on Signal Processing,2005,52(9):2407-2423. [11]CHOIY H.Doubly constrained robust beam form ing m ethod using subspace-associated power com ponents[J].Digital Signal Processing,2015,42(C):43-49. [12]戴凌燕,王永良,李荣锋,等.基于不确定集的稳健Capon波束形成算法性能分析[J].电子与信息学报,2009,31(12): 2931-2936. DAI Lingyan,WANG Yongliang,LI Rongfeng,et al. Performance analysis of robust capon beam form ing based on uncertain set[J].Journal of Electronics&Information Technology,2009,31(12):2931-2936. [13]YUAN X L,GAN L,and LIAO H S.A robust interference convariance matrix reconstruction algorithm against arbitrary interference steering vector m ismatch[J].IEICE Transactions on Fundam entals of Electronics Communications&Computer Sciences,2015,E98.A(7): 1553-1557. [14]林静然,彭启琮,邵怀宗,等.最坏情况下的鲁棒自适应波束形成算法性能分析[J].电子学报,2006,34(12):2161-2166. doi:10.3321/j.issn:0372-2112.2006.12.008. LIN Jingran,PENG Qicong,SHAO Huaizong,et al. Performance analysis of robust capon beam form ing based on worst-case performance optim ization[J].Acta Electronica Sinica,2006,34(12):2161-2166.doi:10.3321/j.issn:0372-2112.2006.12.008. [15]徐定杰,贺瑞,沈锋,等.一种新的稳健Capon波束形成算法[J].宇航学报,2012,33(10):1492-1497.doi:10.3873/j.issn. 1000-1328.2012.10.019. XU Dingjie,HE Rui,SHEN Feng,et al.A new algorithm for robust capon beam form ing[J].Journal of Astronautics,2012,33(10):1492-1497.doi:10.3873/j.issn.1000-1328.2012.10.019. [16]范展,梁国龙,王逸林.一种零陷展宽鲁棒自适应波束形成算法[J].电子与信息学报,2013,35(11):2764-2770.doi: 10.3724/SP.J.1146.2013.00087. FAN Zhan,LIANG Guolong,and WANG Yilin.Robust adaptive beam form ing w ith null w idening[J].Journal of Electronics&Information Technology,2013,35(11): 2764-2770.doi:10.3724/SP.J.1146.2013.00087. [17]MAO X,LIW,LI Y,et al.Robust adaptive beam form ing against signal steering vector m ismatch and jammer motion[J].International Journal of Antennas&Propagation,2015,2015:1-12. [18]阳凯,杨善国.一种宽零陷的自适应波束形成算法[J].电子信息对抗技术,2015,30(2):57-61.doi:10.3724/SP.J.1146. 2013.00087. YANG Kai and YANG Shanguo.An adaptive beam form ing algorithm w ith w ide nulls[J].Electronic Information Warfare Technology,2015,30(2):57-61.doi:10.3724/SP.J.1146.2013. 00087. [19]GU Y and LESHEM A.Robust adap tive beam form ing based on interference covariancem atrix reconstruction and steering vector estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885. [20]庄学彬,陆明泉,冯振明.一种数值稳健且低复杂度的信号子空间估计新方法[J].电子与信息学报,2011,33(1):90-94.doi: 10.3724/SP.J.1146.2009.01392. ZHUANG Xuebin,LU M ingquan,and FENG Zhenm ing.A numerically robust and low-com plexity method of signal subspace estimation[J].Journal of Electronics&Information Technology,2011,33(1):90-94.doi:10.3724/SP.J.1146.2009. 01392. 李立欣:男,1979年生,副教授,研究方向为通信信号处理. 白童童:女,1993年生,硕士,研究方向为阵列信号处理. 张会生:男,1955年生,教授,研究方向为通信信号处理. Improved Double Constraint Robust Capon Beam form ing Algorithm LILixin BAITongtong ZHANG Huisheng BAO Tao SHEN Libin Trad itional doub le constraint robust Capon beam form ing algorithm uses New ton iterativem ethod for solving the optimal loading,presenting the prob lem s of low accuracy and large amount of computation.An im proved Doub le Constraint Robust Capon Beam form ing(DCRCB)algorithm is proposed in this paper.The algorithm reconstructs the signal convariancematrix,and by optim izing the projection of signal steering vector onto the noise subspace,it p rojects the reconstructed interference-plus-noise convariance matrix onto the noise subspace,obtaining the doub le constrain t algorithm m odel based on the noise subspace.For the norm constraint is accessorial,the algorithm model can be converted into a single constraint issue and be solved into an analytical expression of optimal diagonal loading finally.Simulation results show that the im proved algorithm can op tim ize the side lobe by ad justing the beam wid th of themain lobe,im prove effectively the anti-vector error robustness,and reduce the amount of com putation. Adaptive beam form ing;Double constraint Capon beam form ing;Signal convariance matrix reconstrcting;Noise subspace s:The Fundamental Research Funds for the Central Universities(3102014JCQ01052,3102014KYJD034,3102014KYJD040),The Natural Science Foundation Research Project of Shaanxi Province(2016JM 6062),The Aerospace Science and Technology Innovation Fund of CASC TN911.7 A 1009-5896(2016)08-2014-06 10.11999/JEIT 151213 2015-11-03;改回日期:2016-03-31;网络出版:2016-05-24 李立欣lilixin@nwpu.edu.cn 中央高校基本科研业务费专项资金(3102014JCQ01052,3102014KYJD034,3102014KYJD040),陕西省自然科学基础研究计划(2016JM 6062),中国航天科技集团公司航天科技创新基金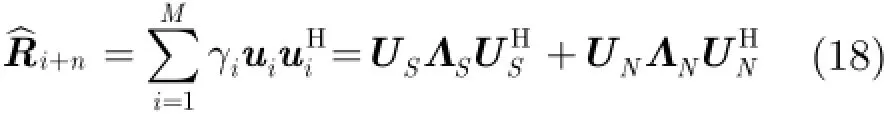

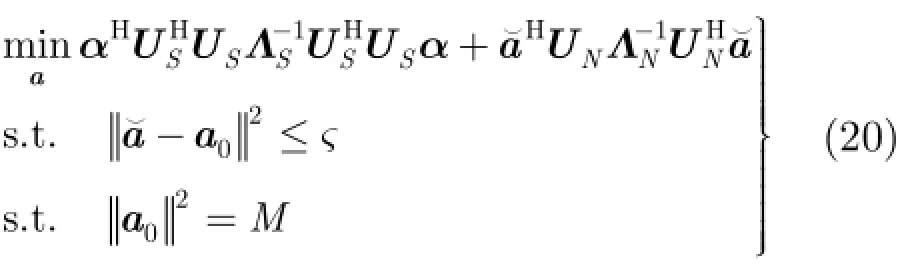
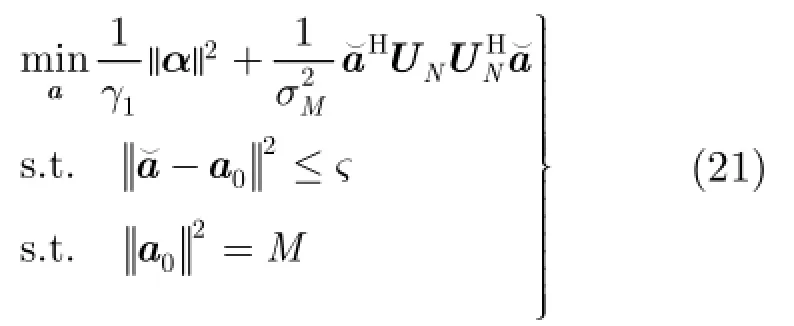
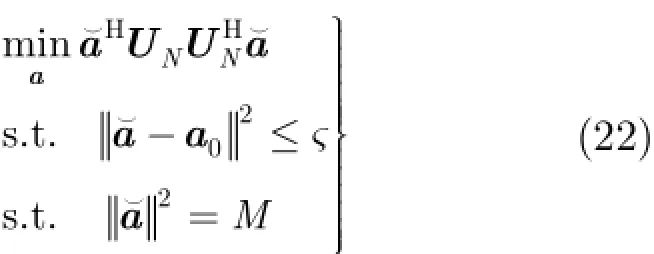
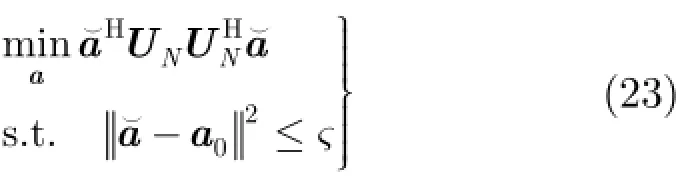

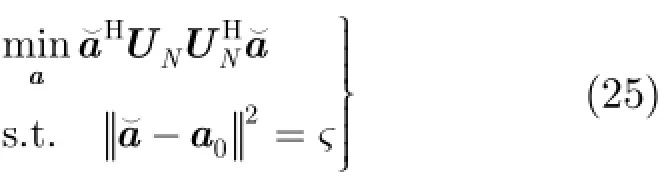
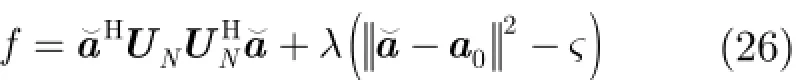
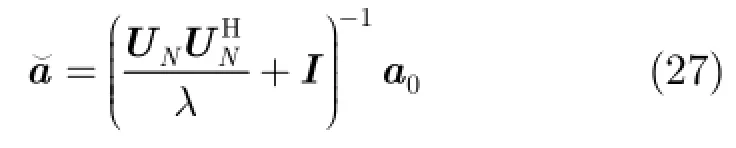
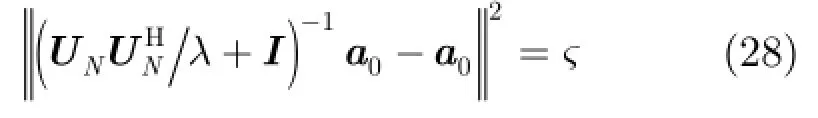
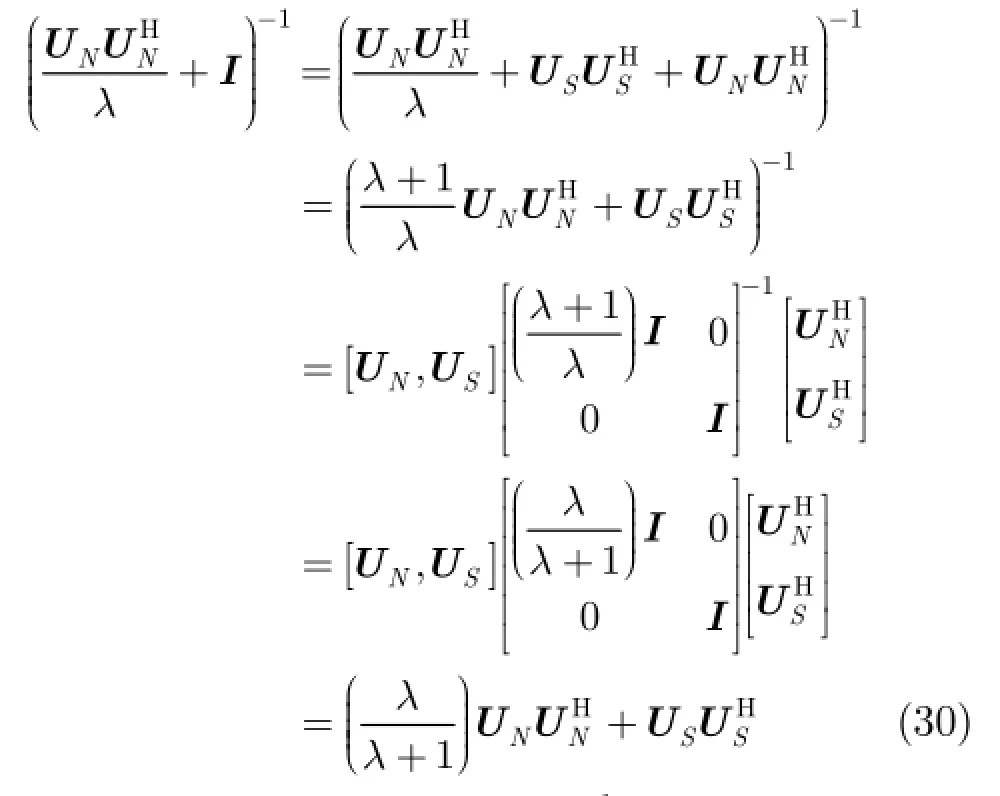
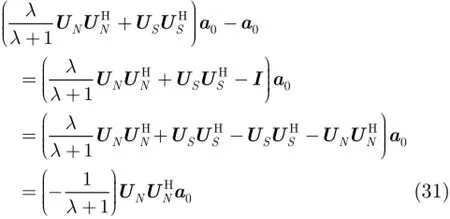
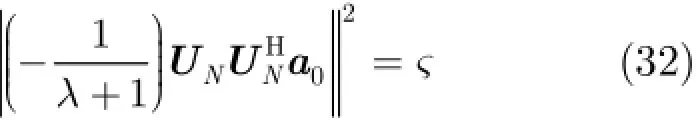
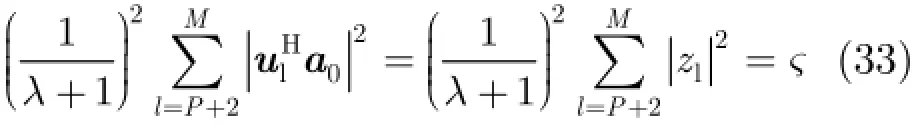
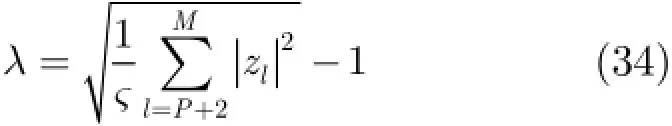
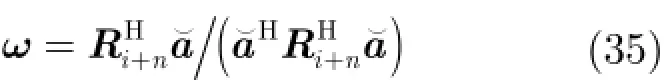
4 仿真分析
5 结论
(School ofElectronics and Information,Northwestern Polytechnical University,Xi,an 710129,China)
