基于复合高斯杂波纹理结构的相干检测
2016-08-30施赛楠水鹏朗西安电子科技大学雷达信号处理国家重点实验室西安710071
施赛楠 水鹏朗 刘 明(西安电子科技大学雷达信号处理国家重点实验室西安710071)
基于复合高斯杂波纹理结构的相干检测
施赛楠*水鹏朗刘明
(西安电子科技大学雷达信号处理国家重点实验室西安710071)
传统的自适应检测器大多是在独立同分布纹理的前提下推导出的。然而,实测海杂波数据中各个距离单元的纹理具有相关性。该文将这一纹理相关性的信息加入到似然比检测中,提出一种基于纹理结构的相干检测器。基于涌浪调制在距离上产生纹理相关性的先验知识,确定与待检测单元纹理相关的距离单元数目,据此可以提供待测单元的纹理信息。实测数据实验表明,该检测器相对于逆伽马纹理复合高斯杂波下最优检测器具有一定的性能提升。
海杂波;复合高斯模型;纹理相关性;自适应检测
1 引言
由于海杂波具有非常复杂的空时变特性,其背景下的雷达目标检测算法的设计往往需要与海杂波的统计特性相联系。雷达低分辨条件下,基于中心极限定理,海杂波的幅度服从瑞利分布。随着雷达分辨率的提高和擦地角的减小,海杂波的幅度明显偏离瑞利分布,并呈现出严重拖尾现象[1]。研究表明,海杂波可以用复合高斯模型建模[1,2]。复合高斯模型可以表示为一个慢变的正随机变量和一个快变的复高斯随机变量的乘积。目前,复合高斯模型下的雷达目标检测问题一直受到广泛关注[3,4]。
文献[5]于1986年提出了一种在复高斯模型下的自适应检测算法,该检测器虽将参考单元数据和检测单元的数据同时带入到似然比中,但是参考单元只起了估计协方差矩阵的作用。文献[6]给出了高斯模型下检测性能最优的匹配滤波(Matched Filter,MF)检测器。在复合高斯模型下,学者们提出了许多的纹理概率模型,典型代表有伽马分布,逆伽马分布(Inverse Gamm a,IG)和逆高斯分布[7]。其中,伽马纹理对应的幅度分布即为K分布模型,该杂波模型下的最优检测器被称为最优K分布检测器(Optimum K-distributed Detector,OKD)[8]。然而,由于检测统计量中存在贝塞尔函数,OKD在实际运用中计算量大,不满足实时性和简单性的工程要求。随后,一批学者采用逆伽马纹理的复合高斯模型拟合实测海杂波数据,该模型对重拖尾的海杂波具有很好的拟合效果[911]-。文献[10]推导了逆伽马纹理复合高斯模型下的最优相干检测器,称之为广义似然比检测线性门限检测器(Generalized Likelihood Ratio Test-Linear Threshold Detector,GLRTLTD)。由于具有简单的表达式,该检测器在实际检测问题中具有可实行性。
近年来,一类基于知识辅助(Know ledge-Aided,KA)的信号处理方法引起了研究者的关注[12,13]。基于知识辅助是指利用某些先验信息,以此提高检测性能。对于先验知识的使用,主要可以划分为两种基本途径。第1种是利用先验知识对采集的数据进行预处理,从而完成对杂波的抑制。第2种是将先验知识使用到检测结构设计中,从而提高检测性能,这也是本文采用的方法。海杂波可以看成是由大尺度的涌浪调制小尺度的破浪花形成的[1]。基于这一形成机理,海杂波的各个分辨单元在距离上的功率存在差异性。根据这一特性,可以把海杂波分为均匀杂波(即具有完全相关的纹理),相关杂波(即纹理在距离上有相关性)和独立同分布杂波(即纹理独立不相干)[13]。由于纹理在距离上的这一结构特点,在特定的相关系数内,可以找到与待检测单元具有相同纹理的距离单元。基于这一先验知识,我们可以把这部分纹理信息运用到似然比检测中,推导出了一种新的基于纹理结构的相干检测器。在新的检测算法中,参考单元起两方面的作用。一方面为待检测单元提供纹理信息,另一方面提供散斑协方差矩阵的信息。实测数据表明,相对于IG纹理复合高斯杂波下的最优检测器(考虑的是独立同分布纹理),新的检测器具有很好的检测性能。
本文安排如下,第2节推导了基于纹理结构的检测器并证明其恒虚警性质;第3节给出了检测器的自适应版本并且分析了纹理结构;在第4节中,结合仿真数据和实测数据证实了新提出的检测器的有效性;第5节总结全文。
2 基于纹理结构的相干检测器
2.1推导
在脉冲多普勒雷达中,海杂波背景下的动目标检测可以归结为下面的二元假设问题:
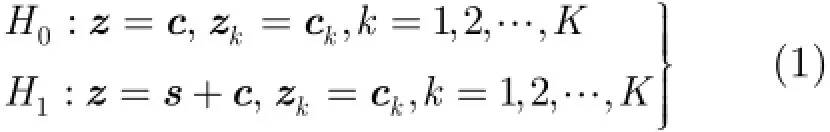
其中,z,s和c分别表示待检测单元接收向量、目标回波向量和海杂波向量,zk表示CUT(Cell Under Test)周围K个纯杂波向量,向量维数为N。H0假设下,检测单元只含有杂波;H1假设下,检测单元含有目标和杂波。
在海杂波建模方面,采用复合高斯模型进行建模,其表示式为
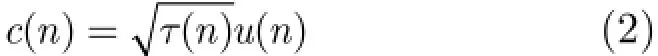
其中,()nт是一个慢变的正随机变量,称为纹理,表示杂波局部功率的变化,是由大尺度的涌浪引起的;u(n)是一个快变的零均值复高斯随机变量,称为散斑,是由破浪花的Bragg散射产生的[1]。当观测时间相当于雷达系统的相干处理时间时,可认为杂波的功率保持恒定。那么,复合高斯模型就退化为球不变随机向量(Spherically Invariant Random Vector,SIRV)模型[3,4,710]-。
为了表示简单,先定义变量:
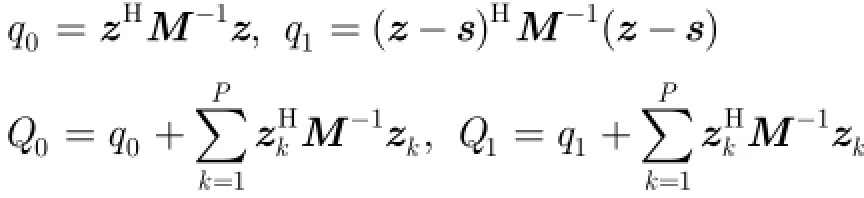
那么,待检测单元和P个参考单元的联合概率密度函数(Probability Density Function,PDF)为
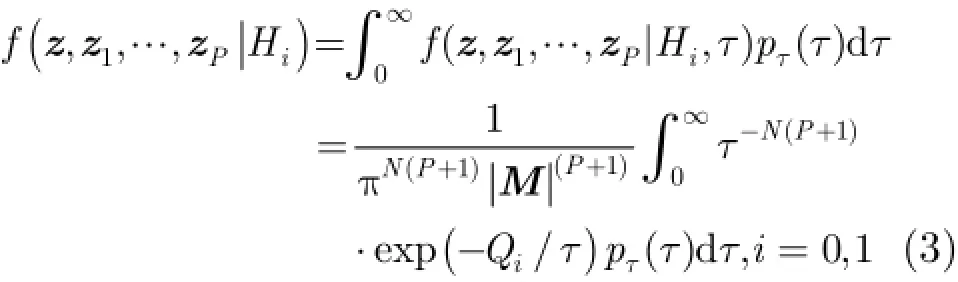
其中,()pтт表示纹理服从的概率密度函数。
假设目标和杂波的协方差矩阵已知,根据奈曼-皮尔逊(Neyman-Pearson,NP)准则,似然比函数为
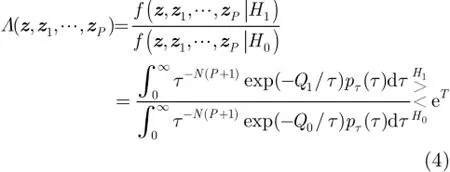
其中,T是依赖于虚警率的决策门限。本文考虑纹理服从IG分布,其形状参数为λ,尺度参数为η,
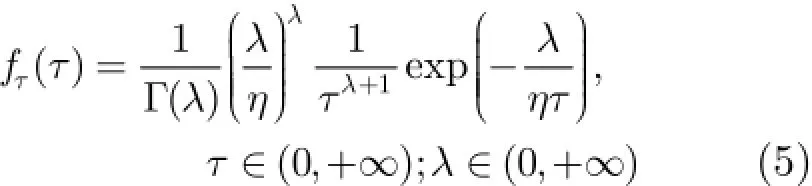
尺度参数与平均功率有关,形状参数反映的是杂波的非高斯性。小的形状参数意味着海杂波幅度分布具有强的非高斯性并表现为重拖尾现象;而λ→∞表明杂波趋向于高斯杂波。
类似于文献[10],将式(5)代入式(4)中。由此得到
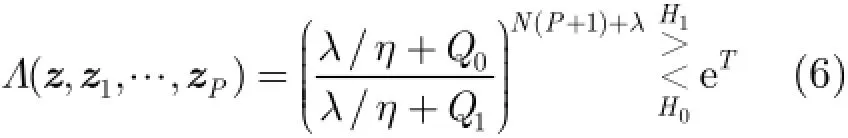
并且,式(6)可以转化为最优检测器的结构[3],即
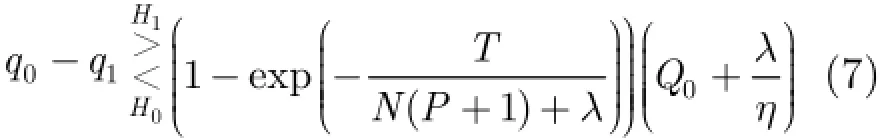
在IG纹理的复合高斯模型下,基于纹理结构的最优检测器等价为匹配滤波器的输出与一个数据依赖项门限的比较,而这个门限是随着接收向量和P个参考单元二次统计量的总和线性变化的。这一特性与文献[10]提出的GLRT-LTD具有相似性。
在一个相干处理时间内,信号可以建模为未知幅度和已知多普勒导向矢量(Doppler steering vector)的乘积,即
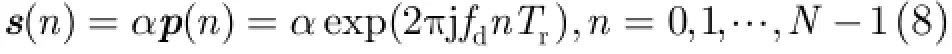
其中,N为累积脉冲数,fd是多普勒频率,Tr是雷达的脉冲重复周期,p为多普勒导向矢量,α是未知的复数,表示信号的幅度。本文考虑信号幅度满足Sw irling 0模型。因此,从待检测单元的接收向量中,采用最大似然估计出信号幅度
最后,将信号幅度估计值带入式(7)中,得到IG纹理下的相干检测器为
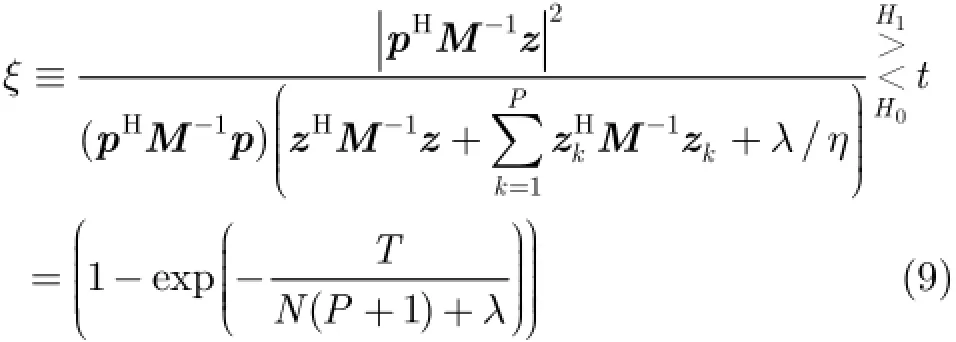
考虑到与GLRT-LTD的相似性,式(9)表示的检测器可以称为基于纹理结构的广义似然比线性门限检测器(Texture-Structure-Based GLRT-LTD,TSBGLRT-LTD)。下面给出GLRT-LTD的统计量[10]
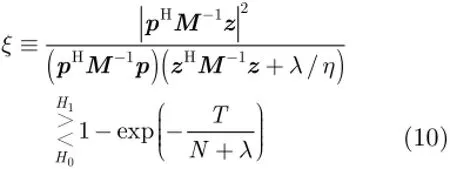
在IG纹理的复合高斯模型下,GLRT-LTD是纹理在距离上独立同分布下的最优检测器。注意式(9)和式(10)两个检测器有两方面不同。第一,两者的检测统计量不同,式(9)中含有部分参考单元的数据依赖项。第二,两者的门限不同,式(9)是关于CUT的数据依赖项和P个参考单元数据依赖项和的线性门限检测,而式(10)只是CUT数据依赖项的线性门限检测器。此外,GLRT-LTD可以看作是TSBGLRT-LTD没有获得纹理信息(即纹理独立同分布,P=0)时的一个特例。
2.2恒虚警特性
恒虚警(Constant False A larm Rate,CFAR)性质是指在某些参数变化时检测器能够保持恒定的虚警率(falsealarm rate)的能力,这对于雷达目标检测来说是重要的特性。因此,有必要对新提出的检测器进行恒虚警特性分析。
在H0假设下,接收向量由纯杂波构成z=c。在已知散斑协方差矩阵条件下,白化后的杂波向量为
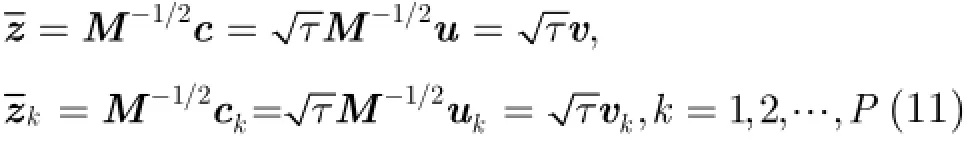
其中,v和kv是白化后的向量,服从均值为零,协方差矩阵为单位阵IN的复高斯分布;т是纹理分量,服从形状参数为λ,尺度参数为η的IG分布。因此,式(9)可以简化为
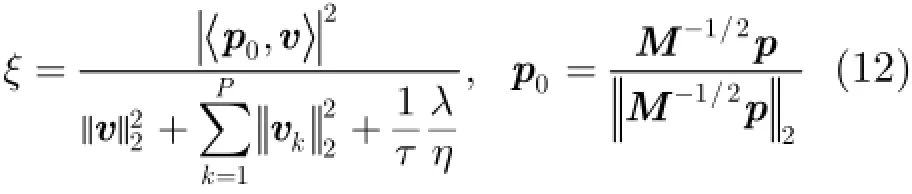
其中,p0表示白化后的多普勒导向矢量,是一个单位复向量。引入酉矩阵是一组与p0正交的单位复向量。那么,式(12)可以化简为
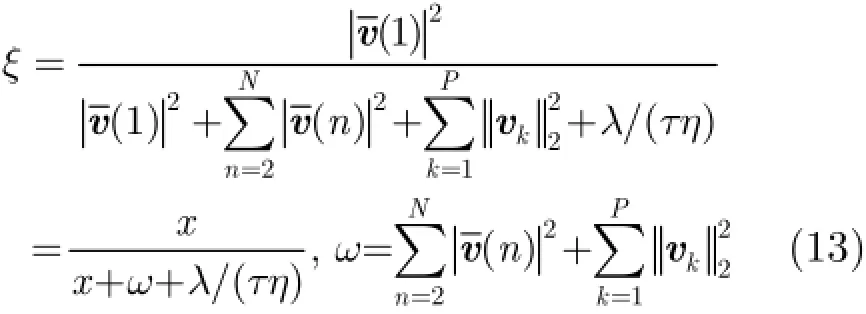
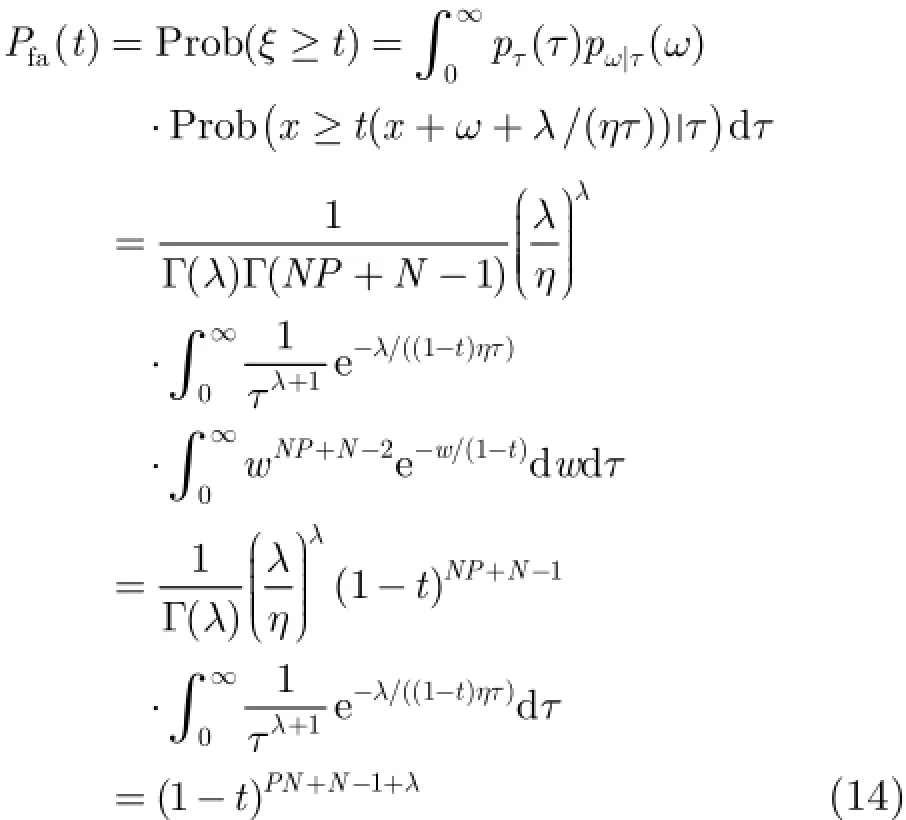
因此,在H0假设下,已知协方差矩阵时,TSBGLRT-LTD的门限为
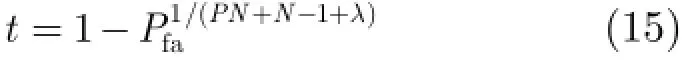
可以从两方面说明式(15)的重要性。一方面,TSBGLRT-LTD的检测门限具有简单的表达式。检测门限由虚警率Pfa,脉冲累积数N,形状参数λ和与CUT具有相同纹理的部分参考单元数目P决定。这相对于蒙特卡洛方法获得门限的方法来说,大大减少了计算量。另一方面,门限对于散斑协方差矩阵M,多普勒导向矢量p和尺度参数η是具有CFAR性质。考虑到实际环境中,海面受风力、风速、环境温度、浪涌等多种自然因素以及雷达设备参数的影响,CFAR性质对于实际环境中检测问题是至关重要的。
3 自适应检测器及纹理结构分析
3.1自适应TSB-GLRT-LTD
基于纹理结构的广义似然比线性门限检测器是在假设散斑协方差已知的条件下推导出的。然而,实际杂波环境中,散斑协方差矩阵是未知的,这就要求获得其估计值。考虑到海杂波在空间上部分均匀和短时间内平稳的,在全局上非均匀和非平稳的特点,可以假设待检测单元和周围的参考单元具有相同的散斑协方差矩阵。因此,可以选取与待检测单元邻近的距离单元,从而获得局部散斑协方差矩阵的估计值。这种方法,可以在大场景的海杂波背景下,实现对于散斑协方差矩阵的自适应检测算法。
将散斑协方差矩阵的估计值代入式(9)检测器中,从而得到自适应的TSB-GLRT-LTD。
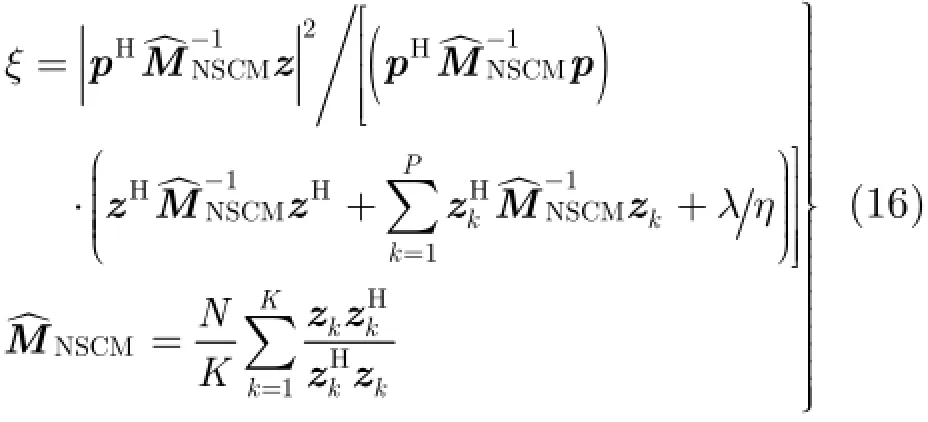
由于本文考虑了纹理在距离上的相关性,杂波是介于独立同分布和均匀情况两者之间。因此,散斑协方差矩阵的估计采用归一化采样协方差矩阵(Normalized Sample Covariance Matrix,NSCM)[14]。这种方法估计简单,无需已知杂波分布模型,在实际中运用广泛。
3.2纹理结构分析
本节对于纹理结构的分析主要包括两部分。一是纹理沿距离维的分布和参数估计,二是纹理沿距离维的相关性。大量实测数据研究表明,海杂波可以使用复合高斯模型进行[14]-。由于实际检测环境中纹理分布的参数未知,自适应检测器还需要估计纹理分布的参数。对于服从式(5)的逆伽马纹理的海杂波,其幅度分布为
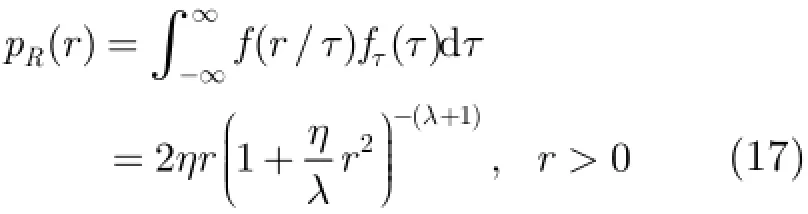
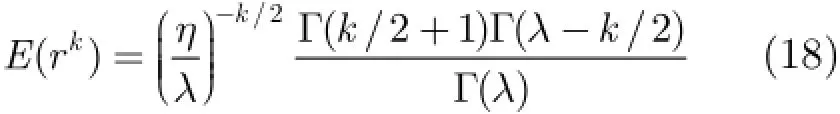
高分辨雷达下,海杂波表现为显著的非高斯性和非平稳性,而且在时间和空间上都有一定的关联性[15]。这里,我们主要分析纹理在距离上的相关性。假设海杂波2维数据x(n,s),n表示时间维,s表示距离维。首先,海杂波时间序列分成长度为L的短向量。从每个短向量中,可以估计出纹理[16]
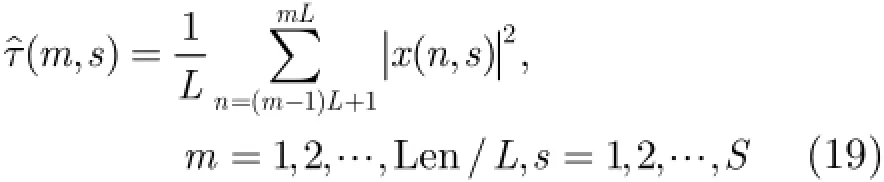
其中,Len表示某一距离单元的序列长度,S为总的距离单元数目。那么,纹理的距离相关系数为
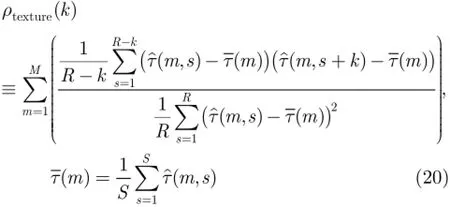
根据式(20),可以估计距离去相关长度和距离完全相关长度。距离去相关长度定义为距离相关函数ρ(k)从1衰减为1/e时对应的距离间隔[15]。当ρ(k)小于时,可以近似认为距离上的海杂波数据不相关。而对于距离完全相关长度,基于现有的知识有以下两个结论。第一,完全相关长度对应的相关系数ρ2是在去相关长度内选取的,即ρ2∈(ρ1,1]。第二,实测数据分析表明,在去相关长度内选取的参考单元可以为CUT提供纹理信息,从而使得检测器有一定的性能提升。但是,最优检测性能对应的P值,目前还没有理论基础研究。因此,本文给出了一种经验选取法。由涌浪调制产生的纹理调制在距离上表现为一个快速衰减的过程,这主要由涌浪尺寸和目前雷达距离分辨率决定的[15]。通过对实测数据的分析和验证,本文经验选取ρ2=0.6。当ρ(k)大于ρ2时,可以近似认为海杂波在距离上的纹理完全相关。
4 实验结果和性能分析
4.1仿真数据检测性能
首先,采用仿真数据对TSB-GLRT-LTD检测器的性能进行了测试。在已知散斑协方差矩阵条件下,根据式(13)进行了105次独立仿真试验,并且检测门限根据式(15)直接获取。参数设置N=8,λ=1.5,10,100,P=0,2,4,8,信杂比(Signal-to-C lutter Ratio,SCR)SCR=-5 dB 。其中,P=0对应的是GLRT-LTD检测器。图1给出了不同形状参数下两种检测器的接收机工作性能(Receiver Operation Characteristic,ROC)曲线比较。可以清楚地看到,由于TSB-GLRT-LTD利用了纹理信息,它相对于最优检测器GLRT-LTD来说有了明显的改善。并且,我们可以得到以下结论。第一,当P增大时,TSB-GLRT-LTD有性能提升。这是因为更多的参考单元为待检测单元提供纹理信息,提高了检测性能。但是当P更大时,性能提升不再明显。第二,形状参数越小,TSB-GLRT-LTD相对于GLRTLTD的性能越提升明显。这是因为小形状参数下,距离维的纹理具有很强的随机性,而新提出的检测器是在减少参考单元纹理随机性下获得性能提升的。第三,当形状参数很大时,两种检测器的性能一致。这是因为,形状参数趋向于无穷大时,杂波趋向于高斯杂波,此时距离维的纹理随机性减弱,部分参考单元提供的纹理信息不再提升性能。
4.2实测数据检测性能
接下来,我们采用实测海杂波数据对自适应TSB-GLRT-LTD检测器进行性能验证。首先,对3组实测海杂波数据进行分析。3组数据都是由X波段的Fynmeet雷达采用VV极化在南非西南海岸于2006年7月27日采集得到的[17]。测试目标为一艘小船,在整个观测时间内,雷达采用跟踪模式对小船进行监测。雷达载频6.9 GHz,距离分辨率15m,雷达脉冲重复频率fr=2.5 kHz。第1组数据(TFA 10_ 002.01.m at)和第2组数据(TFA10_004.02.mat)都是由64个距离单元,99973个相干脉冲序列组成。第3组数据(TFA10_007.02.mat)由64个距离单元,59738个相干脉冲序列组成。为了降低数据的脉冲重复频率,同时不出现谱混叠的前提下,进行下4采样处理,并且删除第14~18个距离单元的数据。图2(a)~图2(c)分别画出了3组海杂波数据的时间-距离幅度图。可以看出第1组海杂波幅度在时间-距离上具有很强的非平稳性,纹理在距离上具有明显的起伏变化。而从第2组到第3组数据,海杂波时空非平稳性相对减弱,趋于平稳。图2(d)~图2(f)分别给出了海杂波数据的经验概率分布曲线和采用IG纹理分布的理论概率分布曲线。3组数据的幅度拟合参数依次为λ=1.9562,η=74.0232;λ=3.6534,η=50.3366;λ=17.6805,η=32.6409。从图2中可知,IG纹理的复合高斯模型对于高分辨小擦地角的海杂波数据具有很好的拟合效果,这为该分布下的检测器性能提升提供了理论依据。
然后,对3组数据的纹理在距离上的相关性进行分析,进而确定与CUT具有相同纹理的距离单元个数P。图3给出了L=128时,两组数据的纹理相关系数与距离单元延迟的关系。可以看出,纹理在距离上的相关函数首先在初始点处出现一个尖峰,然后经历一个快速的下降期,最后出现一个缓慢的衰减[15]。图中灰色直线为10.3679 ρ=对应的值。因此,第1~3组数据对应的去相关距离延迟单元分别为1,1.5和11。而完全相关系数2ρ=0.6时,第1~3组数据的完全相关距离单元数为0.6,1和3。也就是说,对于这3组数据可以近似认为CUT周围分别有1个,2个和6个参考距离单元与CUT具有相同的纹理。
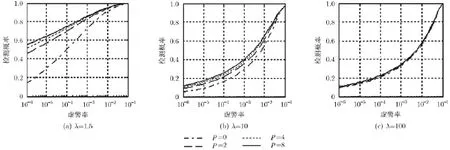
图1 不同形状参数下两种检测器的ROC曲线图
最后,在实测海杂波数据中加入仿真目标,分析在不同信杂比下的检测性能。仿真目标根据式(8)模型产生。平均信杂比定义为为杂波的平均功率。实验中,虚警概率Pfa= 10-4;考虑到3组数据使用的纯杂波数据量的大小,累积脉冲数目N=8;为了减少散斑协方差估计带来的性能损失,参考单元数K=32;P分别取0,2,4,6,8;信号多普勒频率fd在[-fr/2,fr/2]中随机产生,fr= 625 Hz。为了去除多普勒的影响,分别对3组数据10~14个距离单元加上仿真目标分别进行了105次试验,获取平均检测概率。门限通过由蒙特卡洛实验获得。从图4(a)可知,第1组数据在考虑周围两个参考单元,其性能与P=0时相当,P=0对应的是自适应GLRT-LTD,它是独立同分布纹理下的最优检测器。但P值的增加带来了1~2 dB性能损失。这是因为这组数据的功率在距离上起伏大,去相关单元数目为2。在图4(b)中,第2组数据检测性能最好的是P=2。由于考虑了CUT邻近的2个参考单元的纹理信息时,自适应TSB-GLRT-LTD检测器有了1.5 dB的性能提升。而当P=4时,与自适应GLRT-LTD(P=0)dB性能相当;P=6时,明显有0.5 dB性能损失。这是因为第1组数据只有2个距离单元与CUT具有相同的纹理;而当P>4时,纹理在距离上已经去相关了。图4(c)显示了第3组数据的检测性能曲线。P=6对应的自适应TSBGLRT-LTD检测器的性能最好,相对于自适应GLRT-LTD(P=0)提升了1 dB。同时,P=2,4,8相对于P=0时都有一定的性能提升。这是因为根据图3(c),去相关距离单元数为22,认为完全相关的距离单元为6。根据纹理在距离上的相关性这一先验知识,选择合适的P可以获得自适应TSB-GLRT-LTD检测器的性能提升,这得益于纹理结构信息的使用。
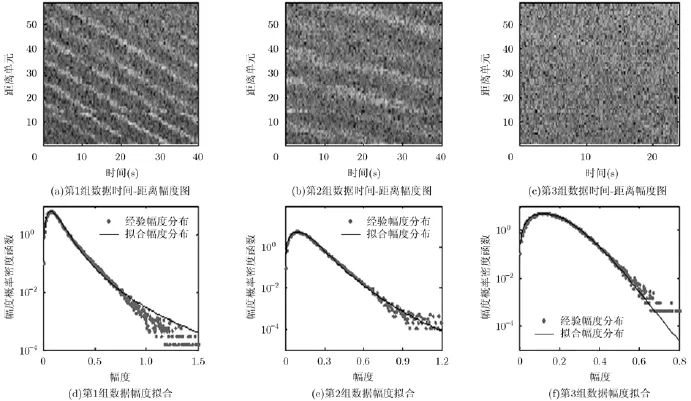
图2 3组海杂波数据的幅度特性
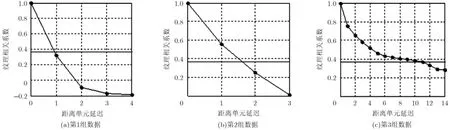
图3 3组数据的纹理在距离维的相关系数
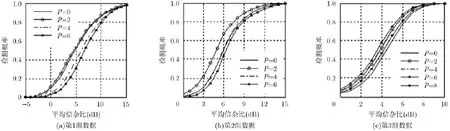
图4 3组数据在不同P值下的检测概率
5 总结
本文将纹理信息运用到检测统计量中,提出了一种基于纹理结构的广义似然比检测线性门限检测器并且分析了其恒虚警性质。基于纹理在距离上相关性的先验知识,确定与待检测单元具有相同纹理的参考单元数目。因此,参考单元为自适应检测器不仅提供了散斑协方差矩阵信息而且提供了纹理信息。实测数据表明,新提出的检测器相对于独立同分布纹理的最优检测器有了一定的性能改善。
[1]WARD K D,TOUG R J A,and WATTS S.Sea Clutter: Scattering,the K Distribution and Radar Performance[M]. London,Un ited K ingdom:The Institution of Engineering and Technology,2006:45-142.
[2]张玉石,许心瑜,尹雅磊,等.L波段小擦地角海杂波幅度统计特性研究[J].电子与信息学报,2014,36(5):1044-1048.doi: 10.3724/SP.J.1146.2013.01139.
ZHANG Yushi,XU Xinyu,YIN Yalei,et al.Research on am p litude statistics of L-band low grazing angle sea clutter[J]. Journal ofElectron ics&Information Techno logy,2014,36(5): 1044-1048.doi:10.3724/SP.J.1146.2013.01139.
[3]SANGSTON K J,GINI F,GERCO M,et al.Structures of radar detection in com pound-Gaussian clutter[J].IEEE Transactions on Aerospace and Electronic System s,1999,35(2):445-458.doi:10.1109/7.766928.
[4]邹鲲,廖桂生,李军,等.基于Bayes框架的复合高斯杂波下稳健检测[J].电子与信息学报,2013,35(7):1555-1561.doi: 10.3724/SP.J.1146.2012.01333.
ZOU Kun,LIAO Guisheng,LIJun,et al.Robust detection in com pound Gaussian clutter based on Bayesian framework[J]. Journal ofElectron ics&Information Techno logy,2013,35(7): 1555-1561.doi:10.3724/SP.J.1146.2012.01333.
[5]KELLY E J.An adaptive detection algorithm[J].IEEE Transactions on Aerospace and Electronic System s,1986,22(1):115-127.doi:10.1109/TAES.1986.310745.
[6]ROBEY F C,FUHRMANN D R,KELLY E J,et al.A CFAR adaptive matched filter detector[J].IEEE Transactions on Aerospace and Electronic System s,1992,28(1):208-216.doi: 10.1109/7.135446.
[7]闫亮,孙培林,易磊,等.基于逆高斯分布的复合高斯海杂波建模研究[J].雷达学报,2013,2(4):461-465.doi:10.3724/ SP.J.1300.2013.13083.
YAN Liang,SUN Peilin,YI Lei,et al.Modeling of com pound-Gaussian sea clu tter based on an inverse Gaussian distribution[J].Journal of Radars,2013,2(4):461-465.doi: 10.3724/SP.J.1300.2013.13083.
[8]DONG Y.Optimal coherent radar detection in a K-d istributed clutter environm ent[J].IET Radar,Sonar& Navigation,2012,6(5):283-292.doi:10.1049/iet-rsn.2011. 0273.
[9]BALLERI A,NEHORAI A,and WANG J.Maximum likelihood estim ation for com pound-Gaussian clu tter w ith inverse gamma texture[J].IEEE Transactions on Aerospace and Electronic System s,2007,43(2):775-779.doi:10.1109/ TAES.2007.4285370.
[10]SANGSTON K J,GINIF,and GRECO M S.Coherent radar target detection in heavy-tailed com pound-Gaussian clutter[J].IEEE Transactions on Aerospace and Electronic System s,2012,48(1):64-77.doi:10.1109/TAES.2012.6129621.
[11]DEMAIO A,FARINA A,and FOGLIA G.Know ledge-aided Bayesian radar detectors&their app lication to live data[J]. IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):170-183.doi:10.1109/TAES.2010.5417154.
[12]邹鲲,廖桂生,李军,等.非高斯杂波下知识辅助检测器敏感性分析[J].电子与信息学报,2014,36(1):181-186.doi:10. 3724/SP.J.1146.2013.00320.
ZOU Kun,LIAO Guisheng,LI Jun,et al.Sensitivity analysis of know ledge aided detector in non-Gaussian clutter[J]. JournalofElectronics&Information Technology,2014,36(1): 181-186.doi:10.3724/SP.J.1146.2013.00320.
[13]CONTE E and DE MAIO A.M itigation techniques fornon-Gaussian sea clutter[J].IEEE Journal of Oceanic Engineering,2004,29(2):284-302.doi:10.1109/JOE.2004. 826901.
[14]GINI F,GRECO M V,and VERRAZZANI L.Detection problem inm ixed clutter environment asa Gaussian problem by adaptive p reprocessing[J].Electronics Letters,1995,31(14):1189-1190.doi:10.1049/el:19950808.
[15]关键,丁昊,黄勇,等.实测海杂波数据空间相关性研究[J].电波科学学报,2012,27(5):943-953.doi:10.13443/j.cjors. 2012.05.026. GUAN Jian,DING Hao,HUANG Yong,et al.Spatial correlation p roperty w ith measured sea clutter data[J]. Chinese Journal of Radio Science,2012,27(5):943-953.doi: 10.13443/j.cjors.2012.05.026.
[16]JAVIER C M,JAVIER G M,ALVARO B C,etal.Statistical analysis of a high-resolution sea-clutter database[J].IEEE Transactions on Geoscience an d Rem ote Sensing,2010,48(4):2024-2037.doi:10.1109/TGRS.2009.2033193.
[17]The Defence,Peace,Safety,and Security Unit of the Council for Scientific and Industrial Research.The Fynmeet radar database[OL].http://www.csir.co.za/small_boat_detection,2014.
施赛楠:女,1990年生,博士生,研究方向为雷达信号处理和微弱目标检测.
水鹏朗:男,1967年生,教授,博士生导师,研究方向为子波理论、图像处理和目标检测.
刘明:男,1986年生,博士生,研究方向为海面微弱动目标检测.
Coherent Detection Based on Texture Structure in Compound-Gaussian Clutter
SHISainan SHUIPenglang LIU M ing
(National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China)
Trad itional adaptive detectors aremostly derived under the assum ption of independent and identically distributed texture.However,the texture correlation along the range cell exists in real sea clutter datasets.A new coherent detector based on texture structure is p roposed by adding the information of texture correlation into the likelihood ratio test.Based on the p rior know ledge that the texture correlation along range is generated by the swellmodulation,the number of range cells related to the texture of the CellUnder Test(CUT)is determ ined,and this number p rovides the information for the texture of CUT.Experimental results using real datasets show that the p roposed detector has better perform ance in com parison w ith the optimal detector in com pound-Gaussian clutter w ith inverse gamma texture.
Sea clutter;Com pound-Gaussian model;Texture correlation;Adap tive detection
The National Natural Science Foundation of China(61201296)
TN959.72
A
1009-5896(2016)08-1969-08
10.11999/JEIT 151194
2015-10-29;改回日期:2016-02-17;网络出版:2016-05-05
施赛楠snshi@stu.xidian.edu.cn
国家自然科学基金(61201296)
