雷达高分辨率紧凑感知矩阵追踪算法
2016-08-30盛明星宋大伟尚社韩崇昭
刘 静 盛明星 宋大伟尚社 韩崇昭
①(西安交通大学电信学院西安710049)②(空间微波技术国家级重点实验室西安710000)
雷达高分辨率紧凑感知矩阵追踪算法
刘静*①盛明星①宋大伟②尚社②韩崇昭①
①(西安交通大学电信学院西安710049)
②(空间微波技术国家级重点实验室西安710000)
针对压缩感知雷达的感知矩阵相干系数随分辨率增加而增大以致不能以大概率对稀疏向量进行完美重构的问题,直接基于原始感知矩阵,提出紧凑感知矩阵追踪(CSMP)算法。该文将CSMP算法应用于十字阵雷达的2维波达方向(DOA)估计并进行了计算机仿真。仿真结果表明与多信号分类(MUSIC)算法,子空间追踪(SP)算法,基追踪(BP)算法和稀疏贝叶斯学习(SBL)算法相比,基于CSMP算法的DOA估计分辨率得到了较大提高。
压缩感知雷达系统;高分辨率;高相关性;紧凑感知矩阵追踪算法
1 引言
压缩感知[1,2](Compressed Sensing,CS)理论指出只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号,可以证明这样的投影包含了重构信号的足够信息。在该理论框架下,采样速率不决定于信号的带宽,而决定于信息在信号中的结构和内容。压缩感知的突出优点是可减少采样数据,节省存储空间。压缩感知将传统的数据采集与数据压缩合二为一,无需复杂的数据编码算法。
压缩感知技术被广泛地应用于雷达信号处理系统中。与传统雷达相比,压缩感知雷达具有以下优点:(1)基于压缩感知技术的雷达信号处理系统根据接收到的回波信号直接进行雷达稀疏场景重构,在接收端免除了匹配滤波器[3],从而最大限度的保持了最大原始量测信息;(2)压缩感知技术采样得到的数据维数远远低于遵循奈奎斯特采样定理采样得到的数据维数,而仅仅与数据稀疏度成正比,从而真正意义上实现了对信息的采集,可以有效减少雷达采样速率和回波数据[4];(3)增加雷达场景的分辨率仅会增加表征雷达场景的稀疏向量的维数,由于表征雷达场景的稀疏向量的维数远远高于雷达量测数量(收发天线数),在雷达收发天线数目固定的情况下,压缩感知雷达系统具备提供高分辨率雷达场景的能力[5]。
虽然在收发天线数量一定的情况下,基于压缩感知技术的雷达系统能获取比普通雷达系统高的分辨率,但是若要进一步提高压缩感知雷达的分辨率则需要解决感知矩阵的相干系数随分辨率增加而增大以致不能以大概率对稀疏向量进行完美重构的问题。目前国内外已经有一系列的工作针对减少雷达感知矩阵的相干性系数展开。大部分工作是通过优化雷达发射波形以减少感知矩阵的相干性系数[6]。文献[7]将压缩感知技术应用于M IMO雷达系统中,并提出一种感知矩阵相干系数极小化波形设计方法,改善了压缩感知雷达目标参数提取的能力。文献[8]推导了相干系数与信号模糊函数的关系,指出针状模糊函数的信号具有较小的感知系数和较高的多维参数联合分辨能力。文献[9]推导了最小化感知矩阵相干系数的波形优化目标函数,并通过模拟退火[10](Sim u lated Annealing,SA)算法对以多相编码信号作为发射波形的目标函数进行优化求解。但是这些工作都需要设计额外的硬件系统来产生特定的波形或实现感知矩阵,而这些硬件系统的设计非常复杂,并在一定程度上增加了雷达的设计成本。
针对感知矩阵的相干系数随分辨率增加而增大以致不能以大概率对稀疏向量进行完美重构的问题,本文基于原始感知矩阵,提出了紧凑感知矩阵追踪(Com pact Sensing M atrix Pursuit,CSMP)算法。首先根据原始感知矩阵中列与列之间的相似距离构造相干性系数较低的紧凑感知矩阵,其每一列对应于原始感知矩阵中的一个相似列组。然后采用正交匹配追踪(OrthogonalMatching Pursuit,OMP)算法基于紧凑感知矩阵得到一个粗略估计支撑集,此时回到原始感知矩阵,粗略估计支撑集对应的若干相似列组中的所有列构成一个候选列集。最后根据原始稀疏向量的稀疏度对候选列集中的列进行排列组合,找到使残差最小的列组合,这个列组合对应的支撑集即为真实的支撑集,从而以大概率实现对稀疏向量的完美重构。与优化雷达波形以减少感知矩阵相干系数的方法相比,本文方法不需要设计额外的硬件系统,算法的复杂度较低。
本文将CSMP算法应用到十字阵雷达的2维波达方向(Direction O f Arrival,DOA)估计上。仿真结果表明,与多信号分类[11](MUSIC)算法,贪婪重构算法子空间追踪[12](Subspace Pursuit,SP)算法,基追踪[13](Basis Pursuit,BP)算法和基于压缩感知的稀疏贝叶斯学习[14](Sparse Bayesian Learning,SBL)算法相比,基于CSMP算法的DOA估计分辨率得到了较大提高。
2 CSMP算法
2.1紧凑感知矩阵的构造
在压缩感知中,重构K稀疏度信号x的关键问题在于找到观测向量y所在的子空间[12]。一旦找到正确的子空间,x中的非零值就可以通过求伪逆求得。贪婪算法最重要的是其找到正确子空间的方法,然而应用贪婪算法找到正确子空间的前提条件是感知矩阵需要满足约束等距性(Restricted Isometry Property,RIP)准则或是其具有较低的相干性系数,但是依赖于实际感知硬件系统的感知矩阵一般具有较高的相干性系数,从而不能实现对稀疏向量的完美重构。本文提出的CSMP算法通过根据原感知矩阵构造具有较低相干性系数的紧凑感知矩阵很好地解决了这个问题。
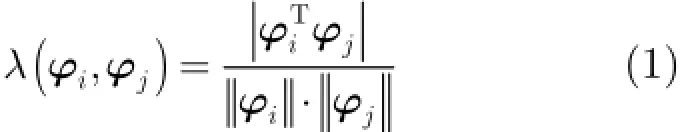
将感知矩阵中所有列映射到一个基于相似度的相似性空间得到许多点,将这些点表示为其中Pφi表示列φi对应的点。相似空间中任意两个点的距离可以定义为
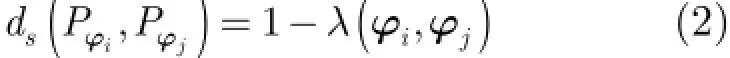
因此,相似距离的分布范围为[0,1],并且相似性空间中两点的距离越小,这两点表示的列的相似性越大。
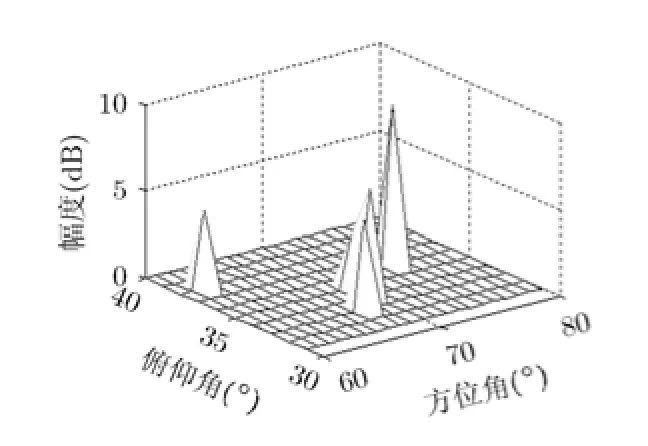
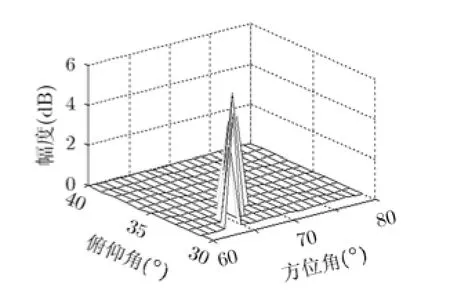
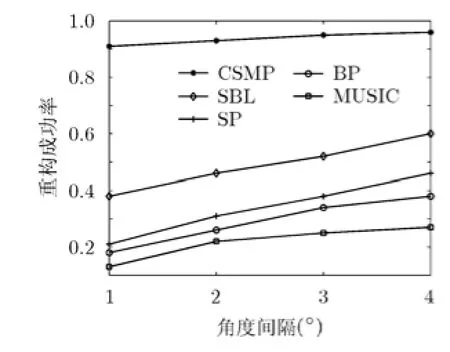
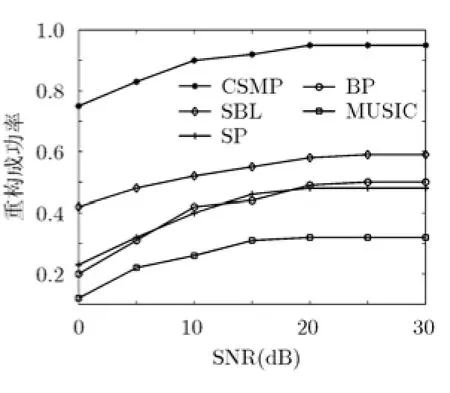
根据相似距离,可以对感知矩阵A中的列应用层次聚类法[15](hierarchical clusteringm ethod)进行分层聚类,将其分为D个列集合:■设M≪D 每个列集合中的列彼此之间非常相似,我们找到可以表示这个列集合的特征的一列,并把这一列称为特征列。对列集合中所有列取平均值来得到特征列,即由这些特征列可以得到紧凑感知矩阵: 紧凑感知矩阵相干性系数讨论:假设紧凑感知矩阵中特征列间最小相似距离为T,即对任意两个特征列则任意两个特征列相似度不大于如果T取较大值,则紧凑感知矩阵将具有低相干性系数。 2.2正确子空间的初始估计 在得到紧凑感知矩阵后,测量向量y可以通过紧凑感知矩阵中的压缩列来表示,即其中是稀疏度为的稀疏向量,为等价测量噪声向量。然后通过OMP算法对其进行粗略恢复,得到正确子空间的初始估计并且将重构误差限制在一定的范围内。其中定义为相似列组iΓ的代表列,i=具体分析过程如下。 对情况(1),ib根据相似列组iΓ获得,1,i= 2,,K…。矢量集合分别对应于列群集合的代表列。的差定义为根据矢量集合的定义,我们可以得到 等效测量噪声的幅度满足 分析完成。 2.3正确支撑集的确定 2.4 CSMP算法的具体步骤 由上述分析,CSMP算法可分为5个主要步骤来描述: 步骤2对紧凑感知矩阵ψ与观测值y应用OMP算法得到正确子空间的初始估计ˆiniS; 步骤3由正确子空间的初始估计ˆiniS找到原始感知矩阵中的候选列集fˆ; 步骤4由候选列集fˆ与稀疏度K找出所有的候选子空间; 3.1十字阵列及信号模型 本文采用非均匀十字阵列模型,如图1所示。 图1 十字阵列模型 此十字型阵列由子阵X和子阵Y构成,分别位于x轴和y轴上。子阵X和子阵Y互成90°,阵元关于原点对称,两条阵列均为均匀线阵,每条线阵上有26个阵元,共有52个阵元,阵元间隔为5mm。 其中s(t)=[s,s,…,s ]T表示K个信源t时刻信号矢1 2 K量;导向矢量矩阵分别为为子阵X和子阵Y的导向矢量,为正或负半轴上第i个阵元的坐标为子阵X和子阵Y接收到的噪声。 3.2感知矩阵的构造 DOA估计中,通常把阵列流型矩阵A进行扩展,形成感知矩阵,使其包含所有可能的空间角度,通常的构造方法为量化法。本文采用空间等网格角度划分法[17]构造感知矩阵,得到式(12),式(13): 本文使用十字阵模型中的感知矩阵,对CSMP,MUSIC,SP,BP和SBL的DOA估计性能进行比较。由于随着空间等网格角度的细化,感知矩阵的相干性系数相应得到提高,因此模型中的感知矩阵具有较高的相干性系数。仿真中的信号源互不相关,且参与比较的算法除了MUSIC算法,都使用单快拍数据,而MUSIC算法使用快拍数为200的阵列输出数据,并找出使谱函数取目标个数的极大值对应的俯仰角与方位角即可。俯仰角和方位角的DOA平面范围分别为 4.1具体场景的重构情况比较 本场景考虑了相距较近的5个目标,分别位于(68°,31°),(62°,36°),(66°,33°),(67°,34°)和(68°,34°)处,信噪比为15 dB,分别应用CSMP,SBL,SP,BP和MUSIC算法对场景进行重构,重构图如图2~图6所示。 从仿真结果我们可以看出,当目标数较多,且其中一些目标相隔较近时,只有CSMP算法能够完全分辨出5个目标,而MUSIC和SP算法分别只能分辨出位于(68°,34°)和(62°,36°)的一个目标,其他4个目标位置均估算错误,BP和SBL算法将5个目标位置全部估算错误,且SBL算法估计出的部分目标信号能量微弱。 4.2不同划分角度间隔的重构成功率比较 使感知矩阵中的方位角与俯仰角角度划分间隔相等,且分别取为1°,2°,3°,4°,每种场景中的信噪比均为15 dB,且都对随机的两个目标进行检测,两个目标的角度最小间隔随着感知矩阵中方位角与俯仰角角度划分间隔的改变进行变化,为1°,2°,3°,4°。分别应用CSMP,SBL,SP,BP和MUSIC算法重构出目标场景,所得的仿真结果如图7所示。 图2 CSMP重构结果的3D效果图 图3 SBL重构结果的3D效果图 图4 SP重构结果的3D效果图 图5 BP重构结果的3D效果图 图6 MUSIC重构结果的3D效果图 从仿真结果我们可以看出CSMP算法在不同的角度划分间隔下的重构成功率都优于其它4种算法。随着角度划分间隔的不断增大,5种算法的重构成功率也逐渐变大。这是因为随着划分角度的增大,感知矩阵的相干性系数相应减小,从而增大了各算法的重构成功率。 4.3不同目标数的重构成功率比较 将随机分布的目标个数分别设置为1,2,3,4个。方位角与俯仰角的角度划分间隔取固定值3°,信噪比为15 dB。分别应用CSMP,SBL,SP,BP和MUSIC算法重构出目标场景,所得的仿真结果图8所示。 从仿真结果我们可以看出CSMP算法在不同目标数情况下的重构成功率都大致优于其它两种算法,且随着目标数的增加,场景的重构成功率相应降低。 4.4不同信噪比环境下的重构成功率比较 将随机分布的目标个数设置为2个。令方位角,俯仰角的等角度划分间隔取固定值3°,信噪比设置为0~30 dB,每次变化5 dB。分别应用CSMP,SBL,SP,BP和MUSIC算法重构出目标场景,所得仿真结果如图9所示。 从仿真结果我们可以看出CSMP算法在不同的信噪比环境下的重构成功率都优于其它4种算法,且随着信噪比的不断增大,5种算法的重构成功率也逐渐变大。CSMP算法的抗噪能力之所以较强是因为应用OMP算法对紧凑感知矩阵和观测向量进行处理得到的粗略估计支撑集这一过程的容错率较高,在一定程度上降低了噪声对其的影响。 图7 不同角度划分间隔的场景重构成功率比较 图8 不同目标数的重构成功率比较 图9 不同信噪比环境下的场景重构成功率比较 针对感知矩阵的相干系数随分辨率增加而增大以致不能以大概率对稀疏向量进行完美重构的问题,本文基于原始感知矩阵,提出了CSMP重构算法。仿真结果表明与传统DOA估计算法MUSIC和基于压缩感知的SP,BP,SBL算法相比,基于CSMP算法的DOA估计的角度分辨率更高。我们未来的工作将致力于改进这种算法,找出使分类最准确的最小相似距离的选取原则以及使其能够处理稀疏度未知的情况。 [1]DONOHO D L.Com pressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.doi:10.1109 /TIT.2006.871582. [2]ZEINALKHANI C and BAN IHASHEM I A H.Iterative reweighted l2/l1 recovery algorithm s for com pressed sensing of block sparse signals[J].IEEE Transactions on Signal Processing,2015,63(17):4516-4531.doi:10.1109/TSP.2015. 2441032. [3]BARANIUK R and STEEGHS P.Com pressive radar im aging[C].IEEE Radar Conference,Boston,2007:128-133. doi:10.1109/RADAR.2007.374203. [4]BAR-ILAN O and ELDAR Y C.Sub-Nyquist radar via dopp ler focusing[J].IEEE Transactions on Signal Processing,2014,62(7):1796-1811.doi:10.1109/TSP.2014.2304917. [5]LI Hongtao,WANG Chaoyu,WANG Ke,et al.High resolution range profile of com pressive sensing radar w ith low computational com p lexity[J].IET Radar,Sonar and Navigation,2015,9(8):984-990.doi:10.1049/iet-rsn.2014. 0454. [6]BOURGAIN J,DILWORTH S,FORD K,et al.Exp licit constructions of RIP m atrices and related problem s[J].Duke M athem atical Journal,2011,159(1):145-185.doi:10.1215/ 00127094-1384809. [7]CHEN C and VAIDYANATHAN P.Com pressed sensing in M IMO radar[C].Asilomar Conference on Signal,System sand Com puters,Piscataway,2008:41-44. [8]SONG Xiaofeng,ZHOU Shengli,and W ILLETT P.The role of the ambiguity function in com p ressed sensing radar[C]. IEEE International Conference on Acoustics,Speech,and Signal Processing,Dallas,2010:2758-2761.doi:10.1109/ ICASSP.2010.5496221. [9]王超宇,梅湄,朱晓华,等.一种稳健的盲稀疏度压缩感知雷达目标参数估计方法[J].电子与信息学报,2014,36(4): 960-966.doi:10.3724/SP.J.1146.2013.01007. WANG Chaoyu,MEIMei,ZHU Xiaohua,et al.A robust blind sparsity target parameter estimation algorithm for com pressive sensing radar[J].Journal of Electron ics& Inform ation Techno logy,2014,36(4):960-966.doi:10.3724/ SP.J.1146.2013.01007. [10]KIM Y G and LEE M J.Scheduling multi-channel and mu lti-tim eslot in tim e constrained w ireless sensor networks via simulated annealing and particle swarm optim ization[J]. IEEE Communications Magazine,2014,52(1):122-129. [11]SCHM IDT R O.M ultiple em itter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280.doi:10.1109/TAP. 1986.1143830. [12]DAI W and M ILENKOVIC O.Subspace pursuit for comp ressive sensing signal reconstruction[J].IEEE Transactions on Information Theory,2009,55(5):2230-2249. doi:10.1109/TIT.2009.2016006 [13]ZHU Hao,GEERT L,and GEORGIOSG.Sparsity-cognizant total least-squares for perturbed com pressive sam p ling[J]. IEEE Transactions on Signal Processing,2011,59(5): 2002-2016.doi:10.1109/TSP.2011.2109956. [14]JI Shihao,XUE Ya,and CARIN L.Bayesian com pressive sensing[J].IEEE Transactions on Signal Processing,2008,56(6):2346-2356.doi:10.1109/TSP.2007.914345. [15]EVERITT B,LANDAU S,and LEESE M.C luster Analysis[M].London:Edward Arnold,2001:121-134. [16]DONOHO D L,ELAD M,and TEM LYAKOV V N.Stable recovery of sparse overcomp lete rep resentations in the presence of noise[J].IEEE Transactions on Information Theory,2006,51(1):6-18.doi:10.1109/TIT.2005.860430. [17]林波,张增辉,朱炬波.基于压缩感知的DOA估计稀疏化模型与性能分析[J].电子与信息学报,2014,36(3):589-594.doi: 10.3724/SP.J.1146.2013.00149. LIN Bo,ZHANG Zenghui,and ZHU Jubo.Sparsity model and performance analysis of DOA estimation w ith com pressive sensing[J].Journal of Electronics&Information Technology,2014,36(3):589-594.doi:10.3724/SP.J.1146. 2013.00149. 刘静:女,1975年生,副教授,博士生导师,从事压缩感知、雷达信号处理方面的研究. 盛明星:男,1991年生,硕士生,研究方向为阵列信号处理、压缩感知. 宋大伟:男,1982年,高级工程师,从事雷达信号处理、微波遥感方面的研究. 尚社:男,1964年生,研究员,从事微波遥感方面的研究. 韩崇昭:男,1943年生,教授,博士生导师,从事多源信息融合方面的研究. Compact Sensing Matrix Pursuit Algorithm for Radars with High Resolution LIU Jing①SHENG M ingxing①SONG Dawei②SHANG She②HAN Chongzhao①①(School ofElectronics and Information Engineering,Xi’an Jiaotong University,Xi’an 710049,China) In this paper,a novel algorithm named Com pact Sensing Matrix Pursuit(CSMP)is p roposed to deal with the high coherence problem encountered in the com pressed sensing based radar system with high resolution. The CSMP algorithm is app lied to the two dimensional Direction O f Arrival(DOA)estimation of cross-array.The simulation resu lts show that the resolution can be increased largely com pared w ith the MUltip le SIgnal Classification(MUSIC)algorithm,Subspace Pursuit(SP),Basis Pursuit(BP),and the Sparse Bayesian Learning(SBL)algorithm s. Com pressive sensing based radar system;High resolution;High coherence;Compact Sensing Matrix Pursuit(CSMP)algorithm s:The Innovation Foundation of CAST(J20141110),The National Natural Science Foundation of China(61573276),The National 973 Program of Ch ina(2013CB 329405) TN957.51 A 1009-5896(2016)08-1950-06 10.11999/JEIT 151135 2015-10-10;改回日期:2016-04-22;网络出版:2016-06-03 刘静elej20080730@gm ail.com CAST创新基金(J20141110),国家自然科学基金(61573276),国家973计划(2013CB 329405)
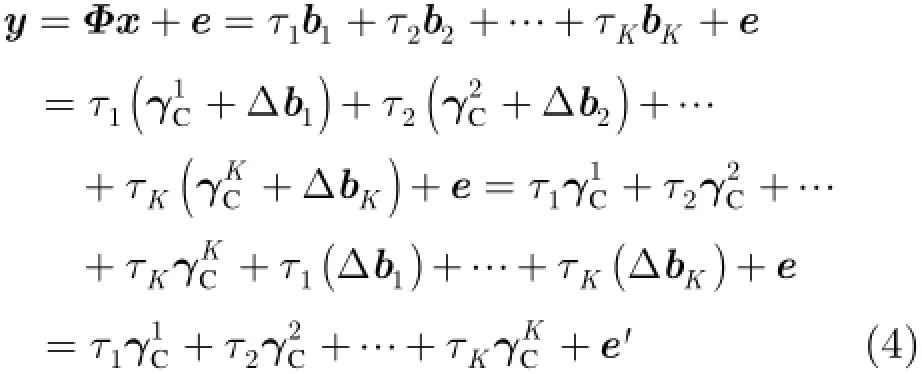

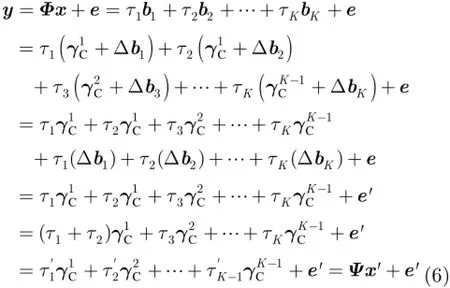
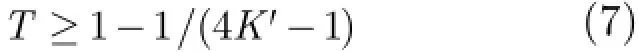
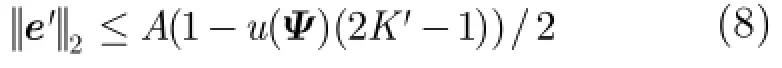
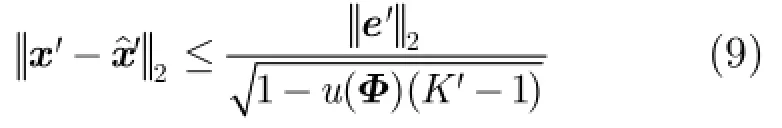
3 基于压缩感知的十字阵雷达2维DOA估计模型

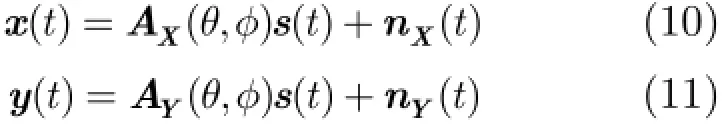
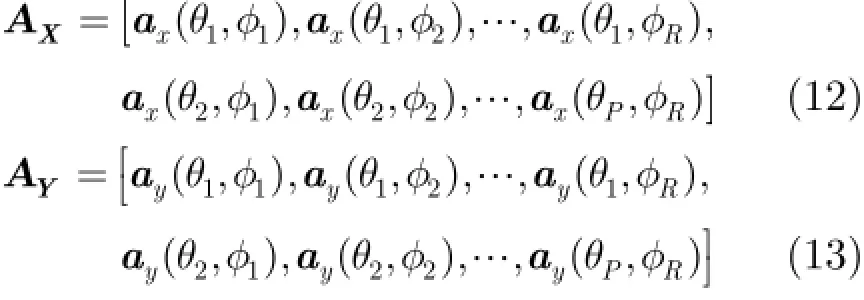
4 仿真结果与分析
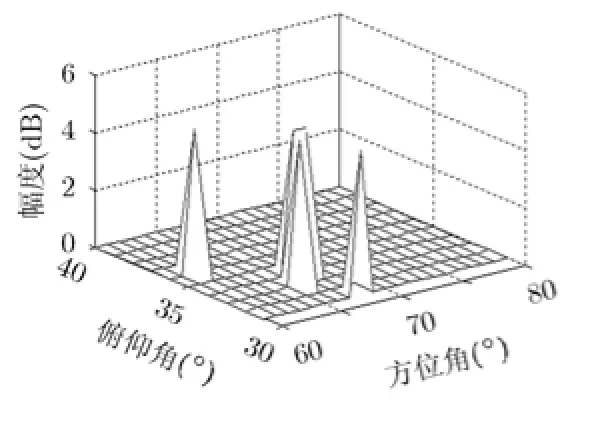
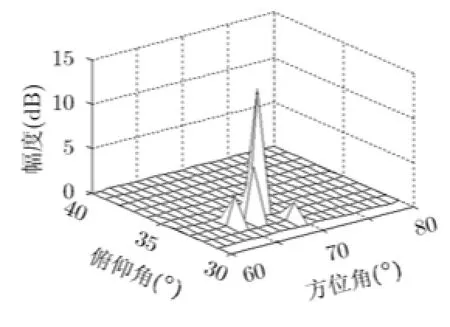
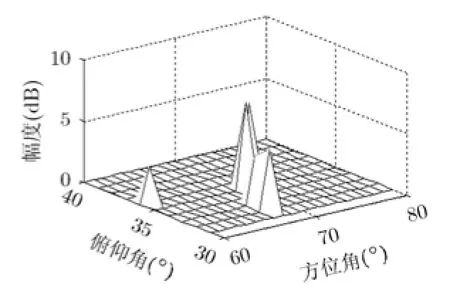

5 结束语
②(National Key Laboratory ofScience and Technology on Space Microwave,Xi’an 710000,China)
