计及非线性容量效应的锂离子电池混合等效电路模型

孙朝晖　成晓潇　陈冬冬　陈国柱

(1.浙江大学电气工程学院　杭州　310027 2.南特大学(法国)电力能源研究所　南特　BP406　44602 3.上海海事大学电力传动与控制研究所　上海　201306)



计及非线性容量效应的锂离子电池混合等效电路模型

孙朝晖1成晓潇2，3陈冬冬1陈国柱1

(1.浙江大学电气工程学院杭州310027 2.南特大学(法国)电力能源研究所南特BP40644602 3.上海海事大学电力传动与控制研究所上海201306)

为提高荷电状态(SOC)估计的精度，对锂离子电池戴维宁(Thevenin)等效电路模型进行了改进。在此模型基础上增加了荷电状态部分，从而使得锂离子电池的非线性容量效应得以体现。将电池的容量分为可用容量与不可用容量，电池容量一分为二的引入能很好的体现电池工作时的额定容量效应、不工作时的恢复效应以及时刻存在的自放电效应。同时，对SOC进行了新定义，通过荷电状态部分的模型来实时估计电池的SOC值，并建立SOC与开路电压之间的一一对应关系。另外，将戴维宁模型中的二阶极化RC网络升级为三阶，并赋予这三阶RC网络实际的物理意义，从而更精确的反映电池的极化效应。最后通过Simulink仿真与实验分析验证了所提出模型的正确性。

荷电状态额定容量效应恢复效应等效电路模型可用/不可用容量

0　引言

储能技术被广泛应用于电力系统及电动汽车等领域，成为当今研究热点。在诸多储能载体中，锂离子电池因比能量大、循环寿命长、自放电小、无记忆效应以及对环境友好等优势得到了广泛关注[1]。为有效模拟锂离子电池，合适的电池模型至关重要。该模型要求能反映电池的荷电状态，能模拟电池的输入和输出电压、电流曲线以及能描述电池的其他一些固有特性，同时要求模型的复杂度较低，精确度较高。为此，专家学者在电池建模方面做了较多研究。常用的电池模型有电化学模型、神经网络模型和等效电路模型。其中等效电路模型是通过电气元件模拟电池对外的暂态和稳态特性，具有建模方法简单、参数辨识容易、精度高、便于融合多种因素、便于数学解析、能对电池SOC全范围领域模拟以及适用性强等优势。

典型的锂离子电池等效电路模型有Rint模型、Thevenin模型和PNGV模型[2- 4]。通常模型都有代表电池极化效应的二阶甚至更高阶的RC网络(如Thevenin模型等)。通过对具体参数R、C的辨识，可以建立精确的模型[5-7]。在模型的复杂度以及精确度之间折中，取二阶或三阶RC网络作为电池的极化内阻较合适。将模型分成荷电状态部分和V-I特性部分，可以在模拟电池暂态和稳态特性的同时反映电池的容量、SOC和运行时间等的变化。作为荷电状态和V-I特性两部分之间的跨接桥梁，一般电池的SOC都与其开路电压之间存在某种非线性的对应关系，可以用Shepherd模型来拟合[8，9]，或者将开路电压与SOC的曲线用最小二乘法分段线性拟合[10]。

KiBaM模型是一种直观的电池模型，能描述电池的非线性容量效应，从而有助于电池SOC的估计以及运行时间预测，然而它不能描述电池的动态V-I特性，也不能与其他电路或系统进行联合仿真[11]。普克特方程能弥补KiBaM模型的不足，有助于定量描述电池的非线性容量效应[12]，然而该方程在拟合锂离子电池曲线方面精度较低。

针对电池的非线性容量效应(包括额定容量效应和恢复效应)，本文提出了一种包括荷电状态部分和V-I特性部分的混合等效电路模型，该模型能在电池大电流放电时更准确地反映电池可用和不可用容量的转换以及与之对应的SOC的变化。对该模型进行了详细分析，确定了模型参数以及对电池SOC进行了新定义[13-16]。最后通过仿真及实验分析验证了所提出模型的正确性和有效性。

1　锂离子电池新模型

1.1描述电池的特性

该模型能描述锂离子电池的如下特性：

1)V-I特性：模拟电池稳态时类似于恒压源的输出特性、暂态时的极化效应以及开路电压随SOC的逐渐变化。

2)自放电：电池内部发生了不可逆反应，造成电池容量的损失。用并联电阻来模拟。

3)极化效应：当电池有电流通过，其内部电极偏离平衡电极电位的现象。用RC网络来模拟。

4)额定容量效应与恢复效应：电池放电倍率越大，其所能释放出的电量越少。然而，在不考虑电池热损耗情况下，由于大放电倍率而没有被释放出的那部分电量即不可用容量，仍储存在电池内。在电池静置或小电流放电一段时间之后，不可用容量会转变成可用容量的现象就是恢复效应。模型中的荷电状态部分能模拟额定容量效应和恢复效应。

1.2有关模型的说明

锂离子电池模型分为荷电状态部分和V-I特性部分，如图1所示。一般对锂离子电池进行充电，充电电流有严格限制(如ICR18650-22P的最大持续充电电流为1 C，即2 150 mA)。而放电电流则相对限制较小，只要小于最大电流10 A即可。故将电池的大倍率充放电研究重点放在放电这一方面，故认为模型中icell为正。另外，电池的各项特性受温度影响较大，暂不考虑温度对电池的影响，实验均在室温25 ℃下完成。图1中，RSEI、CSEI分别为电池电极表面膜层的电阻与电容；RCT、CDL分别为电池电极和电解液之间的传导阻抗；RZw、CZw分别为电池内活性物质和电解液之间的扩散阻抗。

图1　包含非线性容量效应的锂离子电池混合等效电路模型Fig.1　Hybrid equivalent circuit model of lithium ion battery with nonlinear capacity effects

2　模型分析及参数确定

所用电池为三星的锂离子电池，型号为ICR18650-22P。对该电池建立等效电路模型，并确定模型中相关参数的数值。侧重点在于电池模型中的荷电状态部分。

2.1开路电压VOCV

对于锂离子电池来说，其开路电压与电池的SOC有较强的对应关系。然而实际中不宜用端电压法或开路电压法对电池进行精确的SOC估计。原因是：由于充放电模式以及充放电倍率的不同，在同一SOC下，锂离子电池的端电压会有明显差异，不宜用端电压来反映其开路电压；开路电压的获取需要电池静置或小电流放电充分长的时间，费时且低效。

正常工作环境中，电池的开路电压VOCV与SOC关系稳定，受温度影响甚微，可认为开路电压VOCV由SOC惟一决定。通过实验，获得锂离子电池ICR18650-22P在0.1C放电倍率下的放电曲线，如图2所示，可近似认为该曲线为其开路电压随DOD (Depth of Discharge，DOD=1-SOC)变化的曲线。

图2　开路电压VOCV随DOD变化的曲线Fig.2　The curve of open circuit voltage VOCVchanging with DOD

开路电压VOCV与DOD之间的函数关系为

VOCV=f(DOD)=ai·DOD+bi

(1)

式中，i∈[1，n]。

表1列出了每段线性回归的参数，通过R2可知拟合效果较好。VOCV关于DOD的分段函数如式(2)所示。

表1　分段线性表示函数VOCV(DOD)Tab.1　Linearization of the function VOCV(DOD) by means of segmentation of the curve

VOCV(DOD)=

(2)

2.2电容C1和C2

本文所提出的模型中荷电状态部分可以很好地描述电池的非线性容量效应。忽略电池自放电效应，将电池的容量分为可用容量与不可用容量。其中电容C1储存着一部分可用容量，电容C2储存着不可用容量以及另外一部分可用容量，如图3所示。

图3　对所提出的模型中荷电状态部分的分析Fig.3　The analysis to the state-of-charge part of the proposed model

图3中Qavailable、Qunavailable、Qtotal、Q1、Q2等的数学关系如式(3)所示。

(3)

式中，Qavailable为电池的总可用容量；Qunavailable为电池的不可用容量；Qtotal为电池的总容量；Q1为电容C1的容量；Q2为电容C2的容量；U1、U2分别为电容C1、C2的端电压。

由于设计该模型荷电状态部分由两个电容和一个电阻组成，由电池额定容量与额定电压可计算得电池的等效容值C=Qtotal/U1，现需确定模型荷电状态部分两电容容值的比例。电容容值比例与电池的放电倍率密切相关：大放电倍率下，C1中储存的可用容量大大减小；小放电倍率下，C2中储存的不可用容量大大减小，此时荷电状态部分模型中将退化成C1与电流源并联的模型，R2、C2将退化消失。

电池在某一放电倍率下将电能放尽，此时C1端电压为0 V，根据这一性质计算C1与C2的比例。通过统计不同放电倍率下的电池电能放尽所需的时间，可得到各自可用容量的比例，如表2所示。用r表示比例，r、C1、C2为放电倍率I的函数，可得C1(I)=r(I)C以及C2(I)=[1-r(I)]C。下文将给出R2的获取方法，以此确定模型的荷电状态部分。

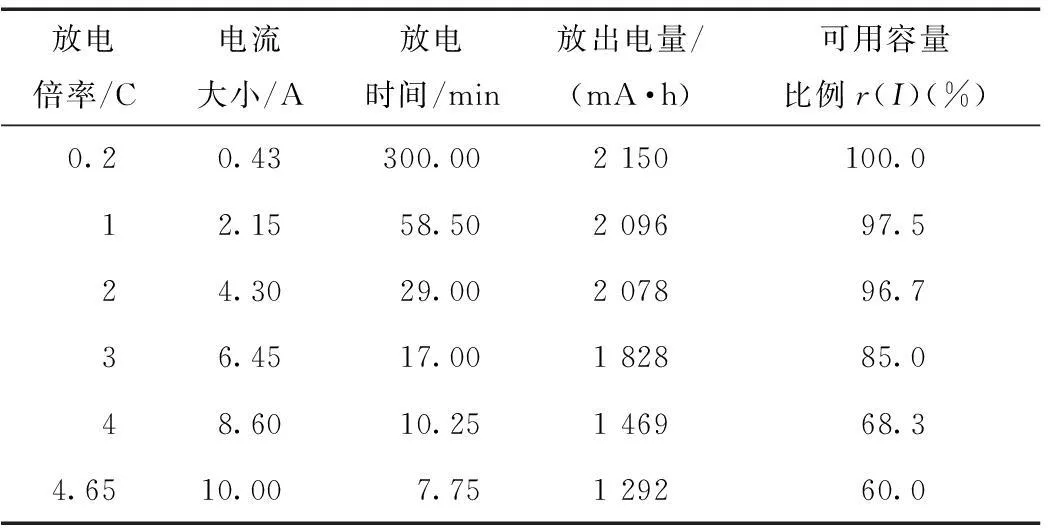
表2　电池各放电倍率下实验数据汇总Tab.2　Experimental data summarize of the battery under different discharge ratio

2.3电阻Rdischarge和R2

对于质量较好的电池，其自放电效应不明显，仅在长时间不用时该效应才会得到明显体现，不做深究，认为并联电阻Rdischarge较大可将其忽略。

电阻R2的取值涉及电池的非线性容量效应。电容C2放电的速率取决于电阻R2的大小以及两电容之间的电压差。当电容C1上的电压为0 V时，表示电池电能用尽，即SOC为0。两电容上的电量的改变如式(4)所示。

(4)

当电池处于恒定电流I放电状态时，由于电阻R2的存在，电容C1上电压的变化速度比C2的快，而且两电容之间的电压差逐渐增大，即C2中由于两电容的电压差而储存的这一部分电荷是不可用容量。当放电电流减小或电池不放电时，电荷从C2经R2进入C1，直到两电容之间电压差为0 V。因此，相比于大电流放电，电池在小电流放电或静置状态时会有更多的电荷可以被使用。这就解释了电池包括额定容量效应和恢复效应在内的非线性容量效应。解方程(4)可得到式(5)。

(5)

假设初始时刻t0=0， τ0=R2C1C2/(C1+C2)， 电池放电时处于满充状态(充分静置后端电压为4.2 V)，即Q1(t0)/C1=U1(t0)=U2(t0)=Q2(t0)/C2， 可认为C2Q1(t0)/(C1+C2)-C1Q2(t0)/(C1+C2)=0， 则得到化简后的式(6)。

(6)

式中，δ(t)为两电容的电压差，其在描述电池非线性容量效应时是一个很关键的量。

图4为一个电池在恒流放电(持续时间tdischarge)、静置(持续时间toff)、恒流充电(持续时间tcharge)三阶段作用下，其端电压幅值变化曲线。这是一种国际上常用的混合功率脉冲试验(Hybrid Power Pulse Test，HPPT)。通过对该曲线的测试，可以求得电池对应的欧姆内阻，也可以拟合出各极化电阻和极化电容的值。不可用容量u(t)表达式如式(7)所示。

(7)

式(7)指数部分多项式e-t/τ0在时间t较大的情况下趋向于0，可知电池的不可用容量随放电时间增加会逐渐趋近于一个极限值，即式(8)中的umax。umax就是电池放电放尽时仍储存在电池内部的潜在可用容量。通过实验得到在某一恒定放电电流I下电池最终的不可用容量值，式(8)中二式联立可最终求得R2。

(8)

图4　混合功率脉冲试验曲线Fig.4　The curve of the hybrid power pulse test

2.4欧姆内阻与各极化阻容

在恒流放电电流施加于电池的瞬间，电池端电压突降，这是因为该恒流在电池的欧姆内阻上产生了压降。用该段压降除以恒定电流值，可求得欧姆内阻值；在电池电压突降后，会有一段缓慢下降的过程，这是电池的极化效应。极化效应对应的电池端电压变化曲线可由多阶RC并联网络串联，通过对该曲线低频、中频、高频段的模拟，得到电池极化效应对应的模型。同理也可由电池的恒流充电端电压曲线求得欧姆内阻与各极化电阻、电容。

2.5计及不可用容量的SOC定义

基本的SOC定义如式(9)所示，该公式常见于电池小电流倍率放电场合，然而该定义下的SOC未考虑到电池大放电倍率下不可用容量的存在，故而在大电流倍率放电场合SOC估计时使用此种定义，估计精度很不理想。更精确的SOC定义如式(10)所示，能时刻估计当前电池的SOC，并能预测在恒定电流I下电池的剩余工作时间。

(9)

(10)

实际上，电池在放电时，会有额外一部分储存于C2的潜在可用容量转换为不可用容量，导致电池的SOC下降更快。在估计电池SOC时，将电池的非线性容量效应考虑进去(见式(9))，将电池的不可用容量也作为电池损失的电量的一部分，能使估计的SOC数值更加接近真实值。

3　仿真及实验分析

对电池ICR18650-22P进行恒流放电，该电池性能参数见表3。得到电池在各放电倍率下的放电曲线如图5所示。不同倍率下的放电曲线说明电池在大放电倍率下所能释放的电量较小，且端电压较低，充分体现了电池的额定容量效应。极端情况下，该电池在4.65 C放电倍率(10 A)下，仅能放出额定容量的60%，非线性容量效应相当明显。

表3　锂离子电池ICR18650-22P基本特性Tab.3　Fundamental characteristics of lithium ion battery ICR18650-22P

图5　各放电倍率下的锂离子电池的放电曲线Fig.5　The discharge curve of lithium ion battery in various discharge rates

利用放电倍率3 C时测得的放电持续时间及放电容量等数据对之前电池模型的荷电状态部分进行仿真，以此说明电池的恢复效应以及新定义下的SOC的优越性。

表2中，以放电倍率3 C下电池的放电状态变化来说明该模型。在放电倍率3 C(6.45 A)下，电池恒流放电17 min(1 020 s)，共放出额定容量85%的电量。3 C放电倍率下，由实验得电池的不可用容量为umax=2 150-1 828=322 mA·h=1 159.2 As。

式(8)结合放电倍率I=6.45 A下电池的不可用容量值1 159.2 As，可解得R2=0.199 Ω。根据实验数据确定模型荷电状态部分的参数后，可以对荷电状态部分进行仿真，仿真结果如图6所示。

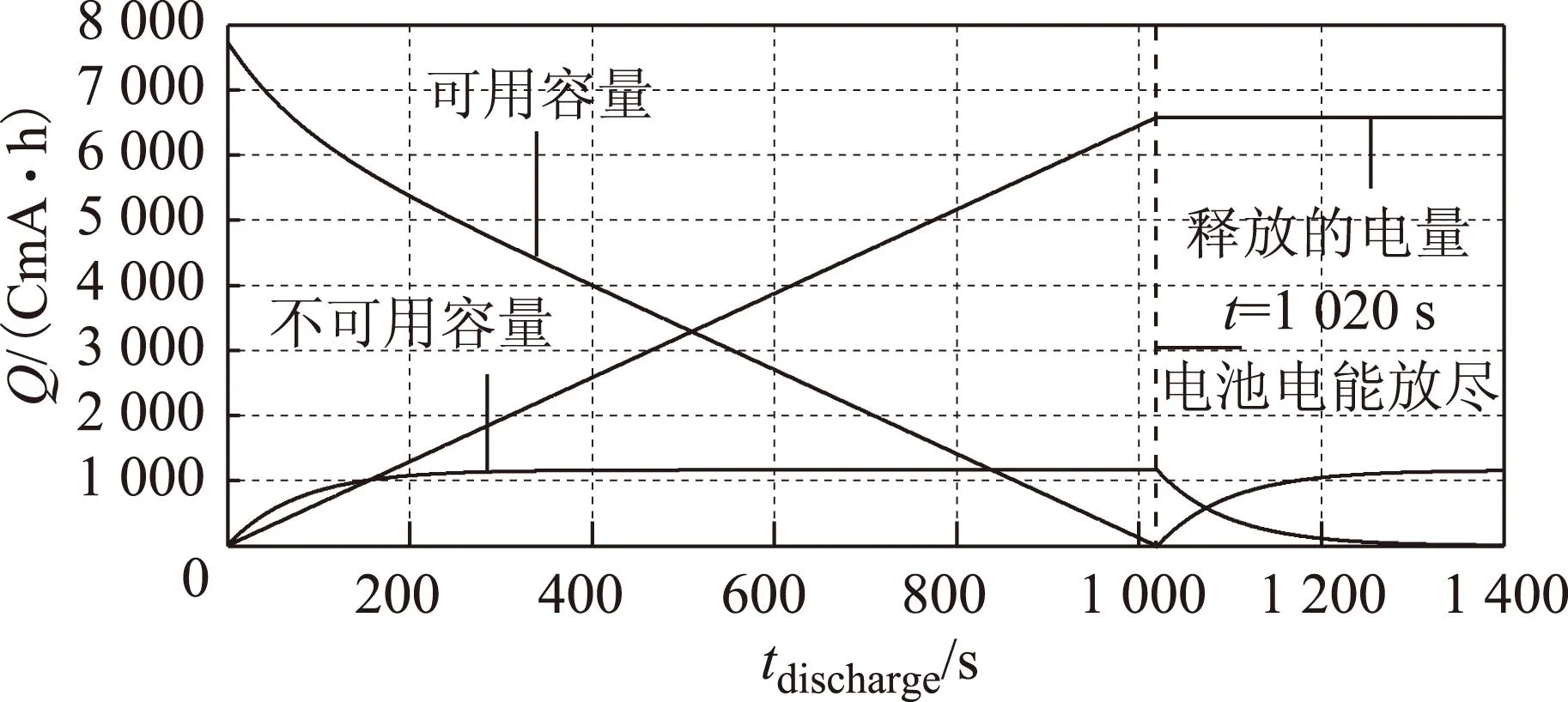
图6　电池模型中可用容量和不可用容量的变化Fig.6　Change of available capacity and unavailable capacity in the battery model

图6反映了电池在大电流倍率3 C(6.45 A)持续放电1 020 s直至电池达到截止电压2.75 V的情况下，电池内部可用容量、不可用容量以及释放的电量的波形曲线。可用容量随时间的增长逐渐下降直到电能放尽，电池断路后储存在C2的不可用容量又逐渐转换为可用容量。不可用容量在电池放电初期增长，逐渐趋近于一极限值，而后不可用容量保持稳定，在电池断路后不可用容量因逐渐转换为可用容量而减小为零。

不考虑电池的非线性容量效应，在1 020 s时电池SOC=0.15，但实验表明这时电池已到达截止电压，故对应的SOC为零更恰当，SOC的基本定义仅适用于小电流放电场合。

图7为不同定义下的SOC曲线。对比基本定义下及新定义下的SOC曲线，结合电池在t=1 020 s时电能耗尽，发现新定义下的SOC曲线更接近实际情况。

图7　不同定义下SOC估计的对比Fig.7　Comparison of SOC estimation with different definition

4　结论

1)对锂离子电池建立混合等效电路模型，将模型分为荷电状态部分和V-I特性部分，用电池的开路电压与SOC之间的函数关系作为连接桥梁。模型中的两部分均能体现锂离子电池各方面的特性，是一个较全面的等效电路模型。

2)该模型针对电池的非线性容量效应，将电池的容量一分为二，分别为可用容量与不可用容量，较好的描述了电池在大电流倍率放电下，容量的衰减，经静置后容量又有所恢复的现象。对模型进行了详细的数学推导，确定了模型荷电状态部分各元件的具体参数，以适应不同放电倍率下仿真的要求。结合仿真和实验数据说明该模型的有效性。

3)在定义SOC时，考虑电池的不可用容量，可以提高电池SOC估计的精度。通过对电池的实际荷电状态以及两种定义下SOC估计的曲线对比，说明新定义的SOC在估计处于大电流放电下的电池方面有优势。小电流放电倍率下，荷电状态部分的模型中R2、C2将退化消失，只剩电容C1与电流源icell并联，此时电池不可用容量恒为0，式(9)与式(10)变为相等。

[1]Omar N，Verbrugge B，Mulder G，et al.Evaluation of performance characteristics of various lithium-ion batteries for use in BEV application[C]//IEEE Vehicle Power and Propulsion Conference，Lille，2010，1-6.

[2]黄贤广，张彩萍.电动车辆锂离子电池电路模型适用性研究[J].电源技术，2011，35(11)：1354-1357.

Huang Xianguang，Zhang Caiping.Adaptability of typical equivalent electrical circuit models to lithium-ion batteries simulation[J].Power Supply Technology，2011，35(11)：1354-1357.

[3]Gholizadeh M，Salmasi F R.Estimation of state of charge，unknown nonlinearities，and state of health of a lithium-ion battery based on a comprehensive unobservable model[J].IEEE Transactions on Industrial Electronics，2014，61(3)：1335-1344.

[4]Feng X，Gooi H B，Chen S X.An improved lithium-ion battery model with temperature prediction considering entropy.in Innovative Smart Grid Technologies (ISGT Europe)[C]//2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe)，Berlin，2012：1-8.

[5]肖蕙蕙，王志强，李山，等.电动汽车动力锂离子电池建模与仿真研究[J].电源学报，2012(1)：41- 44.

Xiao Huihui，Wang Zhiqiang，Li Shan，et al.Modeling and simulation of dynamic lithium-ion battery for electric vehicle[J].Journal of Power Supply，2012(1)：41- 44.

[6]Subburaj A S，Bayne S B.Analysis of dual polarization battery model for grid applications[C]//2014 IEEE 36th International Telecommunications Energy Conference (INTELEC)，Vancouver，BC，2014：1-7.

[7]Pebriyanti G.A lithium-ion battery modeling for a HIL-battery simulator[C]//International Conference on Computer，Control，Informatics and Its Applications (IC3INA)，Jakarta，2013：185-190.

[8]Li Shuhui，Ke Bao.Study of battery modeling using mathematical and circuit oriented approaches[C]//2011 IEEE Power and Energy Society General Meeting，San Diego，CA，2011：1-8.

[9]Bae K C，Choi S C，Kim J H，et al.LiFePO4dynamic battery modeling for battery simulator[C]//2014 IEEE International Conference on Industrial Technology (ICIT)，Busan，2014：354-358.

[10]Rahimi-Eichi H，Baronti F，Chow M Y.Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells[C]//IEEE Transactions on Industrial Electronics，2014，61(4)：2053-2061.

[11]Kim T，Qiao W.A hybrid battery model capable of capturing dynamic circuit characteristics and nonlinear capacity effects[J].IEEE Transactions on Energy Conversion，2011，26(4)：1172-1180.

[12]Utomo A R，Husnayain F，Priambodo P S.Analysis of lead acid battery operation based on peukert formula[C]//2014 International Conference on Electrical Engineering and Computer Science (ICEECS)，Kuta，2014：345-348.

[13]孙丙香，高科，姜久春，等.基于ANFIS和减法聚类的动力电池放电峰值功率预测[J].电工技术学报，2015，30(4)：272-280.

Sun Bingxiang，Gao Ke，Jiang Jiuchun，et al.Research on discharge peak power prediction of battery based on ANFIS and subtraction clustering[J].Transactions of China Electrotechnical Society，2015，30(4)：272-280.

[14]刘红锐，张昭怀.锂离子电池组充放电均衡器及均衡策略[J].电工技术学报，2015，30(8)：186-192.

Liu Ruihong，Zhang Zhaohuai.The equalizer of charging and discharging and the balancing strategies for lithium-ion battery pack[J].Transactions of China Electrotechnical Society，2015，30(8)：186-192.

[15]冯飞，宋凯，逯仁贵，等.磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J].电工技术学报，2015，30(1)：22-29.

Feng Fei，Song Kai，Lu Rengui，et al.Equalization control strategy and SOC estimation for LiFePO4battery pack[J].Transactions of China Electrotechnical Society，2015，30(1)：22-29.

[16]王伟，薛金花，叶季蕾，等.基于SOC调控的用于抑制光伏波动的电池储能优化控制方法[J].电力系统保护与控制，2014，42(2)：75-80.

Wang Wei，Xue Jinhua，Ye Jilei，et al.An optimization control design of battery energy storage based on SOC for leveling off the PV power fluctuation[J].Power System Protection and Control，2014，42(2)：75-80.

Hybrid Equivalent Circuit Model of Lithium Ion Battery Considering Nonlinear Capacity Effects

Sun Zhaohui1Cheng Xiaoxiao2，3Chen Dongdong1Chen Guozhu1

(1.College of Electrical EngineeringZhejiang UniversityHangzhou310027China 2.Institut de Recherche en Energie Electrique de Nantes AtlantiqueNantesBP406，44602France 3.Institute of Electric Drives and Control System Shanghai Maritime UniversityShanghai201306China)

Based on the Thevenin equivalent circuit model of the lithium ion battery，a state-of-charge (SOC) part is added into the model，so as to improve the accuracy of SOC estimation and to embody the nonlinear capacity effect of the lithium ion battery.The battery capacity is divided into two parts，i.e.the available capacity and the unavailable capacity，the introduction of which appropriately describe the rated capacity effect when the battery is working and the recovery effect when the battery is not working.Meanwhile，a new definition of the SOC is given to estimate the SOC of the battery through the state-of-charge part of the proposed model in real-time.And a one-to-one relationship is built up between the open circuit voltage of battery and the SOC.Moreover，the second-order polarization RC network in the Thevenin equivalent model is upgraded into a third-order one，with real physical significance added to the third-order RC network in order to make the polarization effect more accurate.Finally，the simulation waveforms within Simulink indicate the validity of the proposed model.

State of charge，rated capacity effect，recovery effect，equivalent circuit model，available/unavailable capacity

2015-08-11改稿日期2015-11-15

TM315

孙朝晖男，1990年生，博士研究生，研究方向为新能源和分布式发电并网。

E-mail：sun900215@126.com

陈国柱男，1967年生，教授、博士生导师，研究方向为电力电子与电能质量控制、新能源和分布式发电并网等。

E-mail：gzchen@zju.edu.cn(通信作者)

国家自然科学基金资助项目(51177147)。