主动配电网孤岛划分的混合整数规划模型

汪隆君　郭俊宏　王　钢　钟　庆

(华南理工大学电力学院　广州　510640)



主动配电网孤岛划分的混合整数规划模型

汪隆君郭俊宏王钢钟庆

(华南理工大学电力学院广州510640)

无功平衡是制约孤岛可行性和安全性的重要因素，而作为主动配电网主要无功电源的分布式电源自身功率特性常常被忽视，使孤岛功率平衡难以满足。为调和模型求解速度与准确度的矛盾，构建了一种主动配电网孤岛划分的混合整数规划模型。该模型基于解析几何模型线性化DG的P-Q功率极限，有效计及了双馈风力发电机、同步发电机和逆变型发电机的功率特性；通过双线性模型线性化含电压功率乘积项的基尔霍夫电流方程；分离约束模型解决孤岛网络拓扑变化和负荷切除的问题；采用特殊排序集合2线性化平方项。通过算例验证了所提模型，结果表明：所提模型求解准确度高、适应性好，DG运行点满足功率特性，符合工程实际；合理化分段数取值是保证孤岛方案可行性和模型求解准确度的关键，推荐取分段数大于等于12，但其与求解CPU时间无单调关系。

主动配电网孤岛划分分布式电源混合整数规划模型解析几何双线性模型

0　引言

分布式电源(Distributed Generation，DG)具有发电方式灵活和环境友好等优点，越来越多地接入配电网[1- 4]。DG能就近向负荷供电形成独立的自治电力系统，该系统被称之为孤岛，其运行方式被称为孤岛运行方式。合理的孤岛运行方式能有效发挥DG优势，提高系统供电可靠性和供电质量，得到业界的广泛关注。IEEE推荐的DG并网接口标准IEEE1547[5]鼓励供电方和用户尽可能通过技术手段实现孤岛运行，并在经济方面达成共识。作为DG接入点，配电系统不仅是直接影响用户供电可靠性和供电质量的重要环节，更是灵活互动智能用电的实现地，其控制方式直接影响分布式能源的消纳程度。研究表明[6]：在相同网络基础设施条件下，实施主动管理技术可集成的分布式能源比例是被动管理技术的3倍。CIGRE.C6.11工作组将采用主动管理技术的配电网定义为主动配电网[7]。

围绕主动配电网孤岛划分问题，国内外研究者展开一系列有益的探索，取得阶段性进展，主要有以下几类：

1)启发式方法[8，9]。以DG为根节点，通过深度优先搜索或广度优先搜索方法，求解以等值有效负荷最大为目标、功率平衡为约束的孤岛划分模型。该方法求解快，但其孤岛形成过程依赖节点编号顺序，形成的孤岛存在不确定性。

2)约束满足模型[10，11]。将孤岛划分问题转换为约束满足的布尔型决策问题，将一系列约束形成决策图，大幅收缩解空间规模，并对收缩后解空间中的解逐一作校验及排序，获得孤岛划分方案。该方法需要对可行解空间的解逐一校验，当可行解空间较大时校验排序耗时严重。

3)搜索加校验方法[12-15]。具有代表性的文献[14]将孤岛划分问题转换成多个树背包问题，即先逐一对单个DG以有功平衡为约束形成孤岛，再对单DG孤岛进行合并；通过可行性检验和若干次调节获得近似最优孤岛方案。该算法中孤岛合并的基础是某个负荷与多个单DG孤岛相连，而多个单DG孤岛一起向邻近负荷供电的情况不能被有效考虑，且校验过程涉及多次潮流求解。

4)人工智能优化算法[16，17]。采用遗传算法、粒子群算法和差分进化算法等对含DG配电网孤岛进行划分，其随机搜索所获方案常常难以满足孤岛运行约束，从而产生大量的不可行解，丢弃/修正过程耗时，且早熟现象和解不稳定性使该方法距工程应用还有较大差距。

5)数学规划方法[18，19]。建立了分布式电源联合供电表达式和配电网孤岛划分数学模型，采用混合整数规划(Mixed Integer Programming，MIP)方法进行求解。鉴于MIP算法具备全局寻优能力，将主动配电网孤岛划分模型线性化后再求解，不仅能高效稳定获得全局最优解，还调和了求解速度与准确度的矛盾。

无功平衡是制约孤岛可行性和安全性的重要因素[20]，而DG在保证主动配电网无功平衡方面发挥着重要作用[21]。上述5类孤岛划分模型及方法具有共同局限性：①忽视了DG自身功率输出特性，若有功和无功功率分别满足区间约束，即DG功率特性为盒式约束，这将导致孤岛运行点超出DG的P-Q功率极限，从而高估了孤岛供电能力，背离工程实际；②DG功率输出与电压无关，而工程中DG功率输出是电压的函数，根据负荷需求调节DG出力和节点电压。

鉴于MIP模型能高效可靠地全局收敛，在分析DG并网类型分类及功率特性的基础上，本文构建了一种主动配电网孤岛划分的混合整数规划模型。该模型基于解析几何模型线性化DG的P-Q功率极限，有效计及了双馈风力发电机、同步发电机和逆变型发电机的功率特性；通过双线性模型线性化含电压功率乘积项的基尔霍夫电流方程；分离约束模型解决孤岛网络拓扑变化和负荷切除的问题；采用特殊排序集合2线性化平方项。通过算例验证了所提模型的适应性和精确性。

1　DG功率曲线及其线性化

1.1DG的P-Q功率极限

按DG与主动配电网接口的方式划分，主要有以下3种：双馈式感应风力发电机(Doubly Fed Induction-Based Wind Generator，DFIG)、同步发电机(Synchronous Generator，SG)接入型和逆变器(Voltage Source Inverter，VSI)接入型。

DFIG能根据风速状况实时调节发电机转速，令风力发电机在最佳叶尖速比附近运行，优化风力发电机运行效率。DFIG的定子直接相连于电网，转子通过变换器并网，其总输出功率等于定子侧输出功率和网侧变换器输出功率之和。定义发出功率方向为正、吸收功率方向为负，其输出功率在“d-q”坐标系下表示为

(1)

PT，DFIG=PS，DFIG+PC，DFIG

(2)

QT，DFIG=QS，DFIG+QC，DFIG

(3)

PT，DFIG=(1-s)PS，DFIG

(4)

PC，DFIG=-sPS，DFIG

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

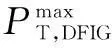
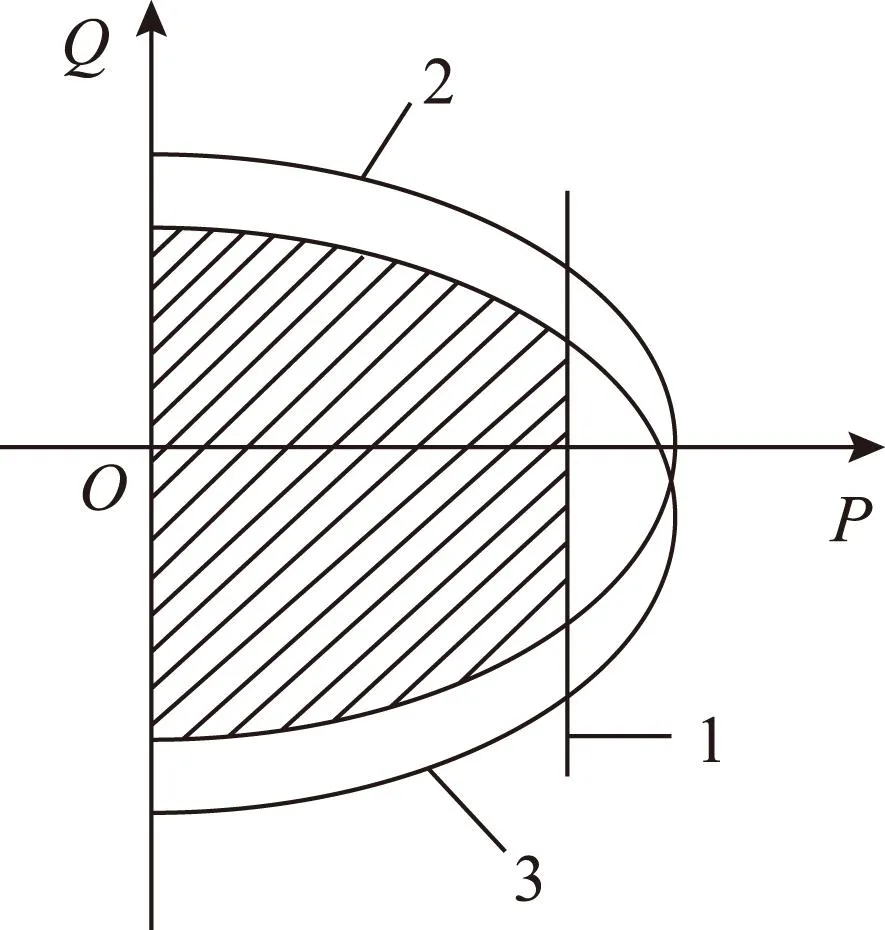
图1　双馈风力发电机P-Q功率曲线Fig.1　Power curve of DFIG

图1中，直线1表示原动机出力的限制，即式(1)；曲线2表示考虑网侧变换器时定子电流限制，即式(2)～式(8)和式(12)～式(14)；曲线3表示考虑网侧变换器时转子电流限制，式(2)～式(5)、式(9)～式(14)。这些线条围成的阴影区域构成DFIG的功率输出特性，其边界即为DFIG的P-Q功率极限曲线。将阴影区域边界的解析方程简化绘于图2a。

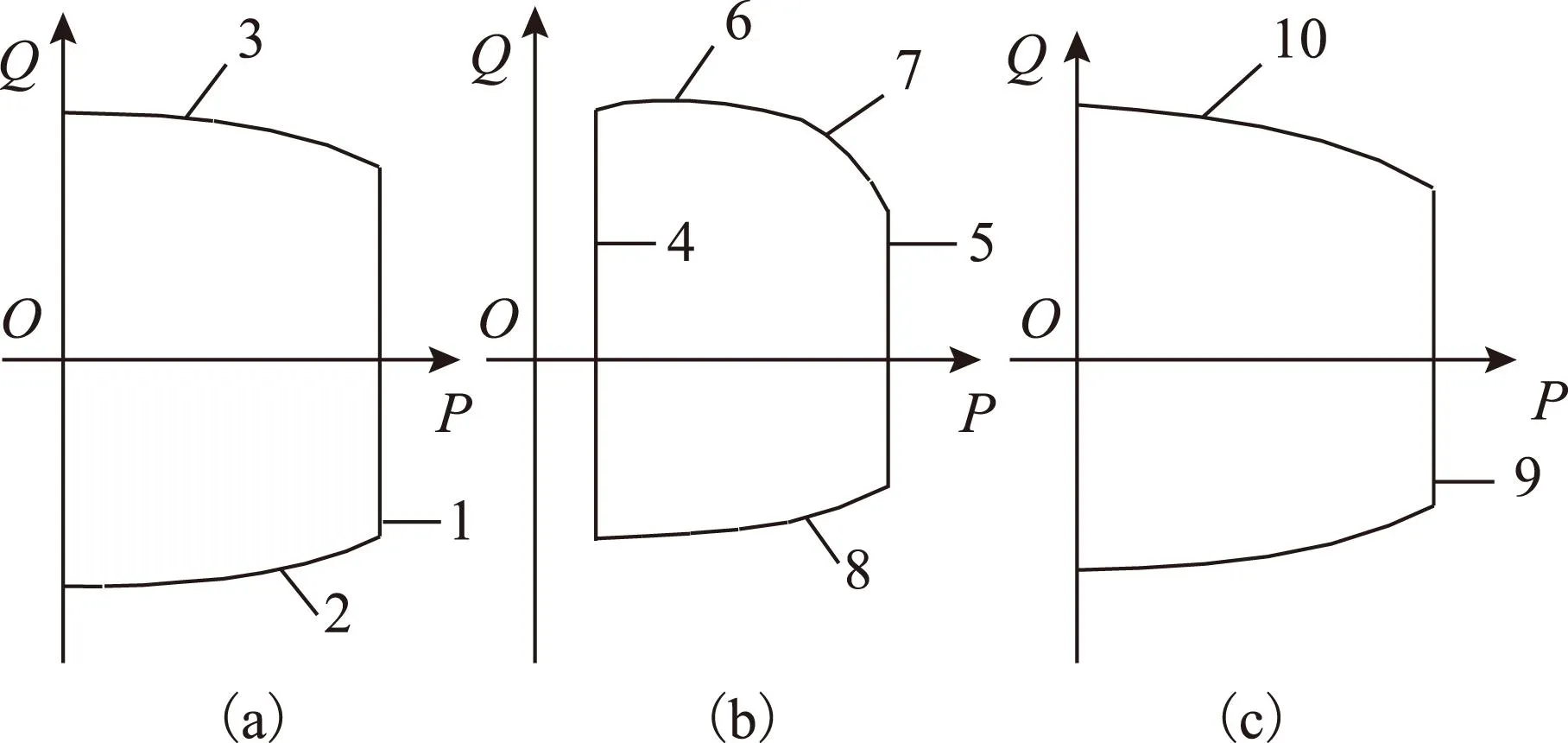
图2　DG的P-Q功率极限Fig.2　P-Q capability limitation of DGs

SG-DG与电网直接相连，若保持原动机输入功率不变，仅调节其激磁系统，可控制无功功率输出，方程表示为

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

VSI-DG常采用直流电压/无功功率外环、电流内环控制，向网络输送有功功率的同时，经逆变器并网可输送无功功率，在一定程度上可对电网进行无功补偿。逆变器并联交流电网运行，其功率损耗小，可忽略不计，因此逆变器的输出电流决定了VSI-DG的输出功率，其方程表示为

(23)

(24)

(25)

(26)

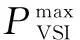
1.2解析几何线性化模型

以VSI-DG为例，说明P-Q功率极限曲线的线性化原理。式(23)～式(26)围成的区域，可写成

(27)式中，SVSI为VSI-DG容量。从解析几何角度看，式(27)表示点(PVSI，QVSI)处于半径为SVSI的圆内。若将圆周n等分，当n→∞时，可将圆近似为内接等n边形，如图3所示。设M、N为圆内接等n边形相邻的两点，M、N的弧度角分别为α、β，则α=2πk/n，β=2π(k+1)/n，k∈[0，n-1]，即点M坐标为(SVSIcosα，SVSIsinα)，点N坐标为(SVSIcosβ，SVSIsinβ)，则等m边形任意1条边MN直线方程可表示为

(28)

因此，式(27)可近似转换为

PVSI(sinβ-sinα)-QVSI(cosβ-cosα)≤SVSIsin(β-α)

(29)

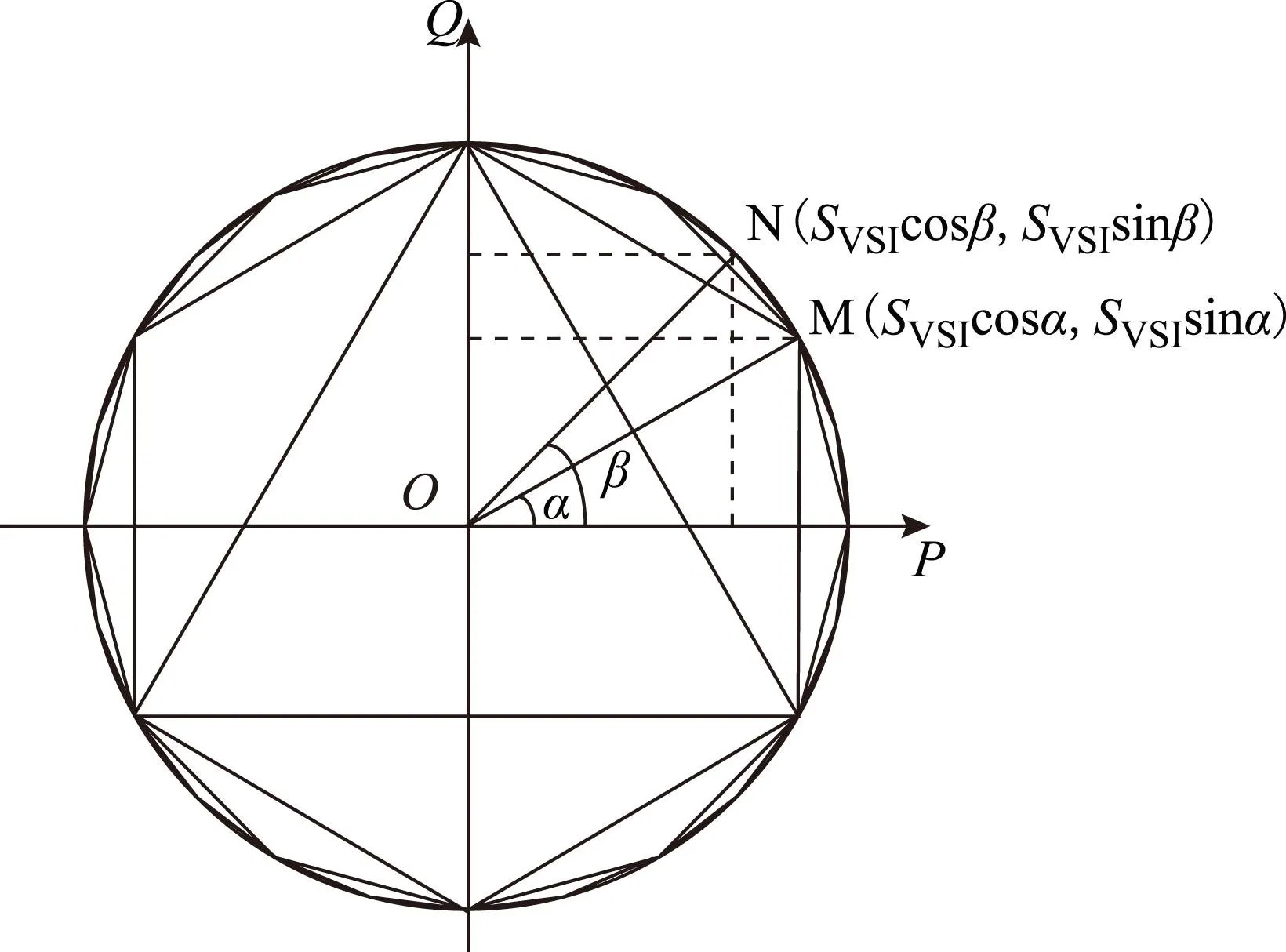
图3　容量约束线性化Fig.3　Diagram of capability constraint linearization

同理，DFIG的功率方程式(6)～式(14)为椭圆方程，利用以上线性化模型处理，得到

PS，DFIG(sinβ-sinα)-QS，DFIG(cosβ-cosα)≤

(30)

(31)

(32)

类似地，SG的功率方程(16)～式(21)线性化为

(33)

PSG(sinβ-sinα)-QSG(cosβ-cosα)≤

(34)

2　孤岛划分MIP模型

2.1目标函数

主动配电网孤岛划分是在配电网满足系统安全运行约束的条件下，通过合理安排各可控DG出力和一系列网络重构的开关操作，使孤岛形成过程中系统负荷削减总量最小，即孤岛形成前后供电负荷偏差最小。这不仅有利于提高供电可靠性，还有助于孤岛重新并网。因此，主动配电网孤岛划分的目标函数为

(35)

式中，Pcut为系统恢复期间负荷削减量；Pdi，t为时刻t节点i的有功负荷；n为时刻数；σi为节点i的负荷投切状态，是01整数变量(1表示切除，0表示运行)。

2.2约束条件

为提高孤岛划分模型求解的收敛性，采用支路电流潮流模型[23]，即以电流实部和虚部为状态变量。根据基尔霍夫电压定律KVL和电流定律KCL，列写方程

(36)

(37)

(38)

(39)

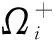
孤岛划分使主动配电网进行网络重构，拓扑存在不确定性，为此将引入01整数变量αij表示支路的通断状态，式(36)和式(37)基于分离约束模型转换为

(40)

(41)

(42)

(43)

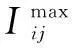
将KCL等式约束的注入电流按照实部和虚部展开为

(44)

(45)

(46)

(47)

(48)

注意到式(45)～式(48)右侧含有2个连续变量乘积项，无法直接应用MIP模型求解。为快速求解上述模型，引入双线性约束条件。设x，y为具有上下限约束的连续变量，满足

x-≤x≤x+

(49)

y-≤y≤y+

(50)

式中，x+和x-分别为变量x的上、下限；y+和y-分别为变量y的上、下限。根据不等式运算法则，易得

x-(y+-y)≤x(y+-y)

(51)

x-(y-y-)≤x(y-y-)

(52)

x(y+-y)≤x+(y+-y)

(53)

x(y-y-)≤x+(y-y-)

(54)

令w=xy展开，得

w≤xy++x-y-x-y+

(55)

w≥xy-+x-y-x-y-

(56)

w≥xy++x+y-x+y+

(57)

w≤xy-+x+y-x+y-

(58)

式(55)～式(58)表示利用4个平面对2个连续变量乘积作约束，平面系数为2个连续变量的上下限。式(44)的ζi，t，ηi，t分别表示时刻t电压实部和虚部与电压幅值平方之比，其上、下限取值可参考文献[24]。

(59)

(60)

(61)

(62)

线路电流和节点电压应满足其幅值约束条件

(63)

(64)

(65)

(66)

w1，t≤z1，t

(67)

wi，t≤zi-1，t+zi，ti>1

(68)

(69)

(70)

3　算例分析

在GAMS平台上搭建本文所提孤岛划分MIP模型，采用商业混合整数规划求解器GAMS/CPLEX进行求解，以下所有算例的测试计算均在Intel(R) Core(TM) i5- 4460 CPU @3.20 GHz，3 GB RAM的Windows 7 SP1 32 bit环境下进行。

以美国PG&E69节点系统[26]为基础搭建算例测试系统1，其额定电压为12.66 kV，含有功负荷为3 802.19 kW，无功负荷为2 694.6 kvar，设线路段均配有分段开关、负荷出线配有负荷开关。不同类型的DG按照表1接入系统，其具体运行参数见附表1～附表3。

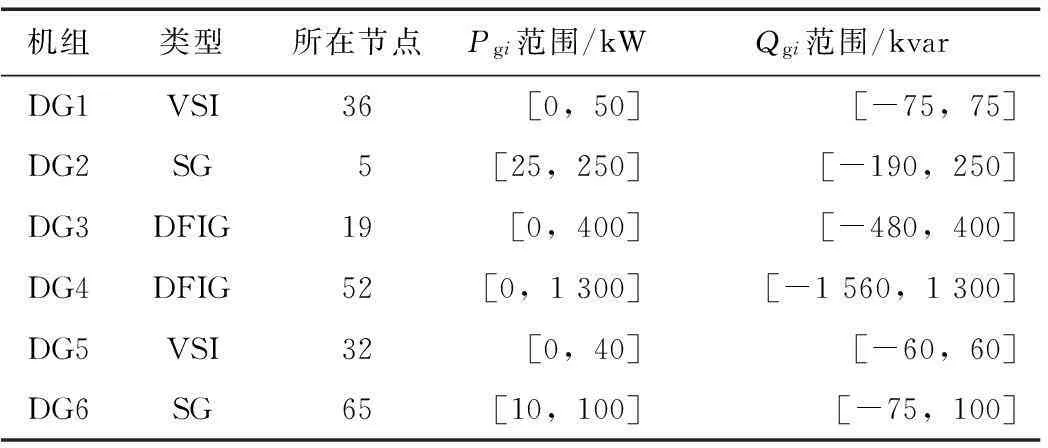
表1　测试系统1分布式电源配置Tab.1　DG configuration of test system 1

设支路2-3发生三相永久短路故障，经故障隔离，故障点下游负荷节点全部失电，所提模型经12.53 s求得孤岛方案如图4所示。图中，虚线范围表示形成的DG孤岛，实心节点表示DG孤岛恢复供电的负荷节点，空心节点表示被切除失电的负荷节点。

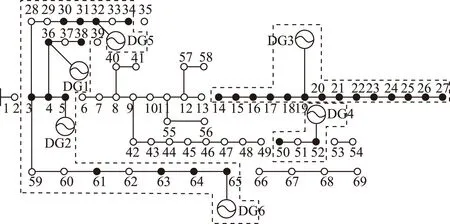
图4　测试系统1孤岛划分Fig.4　Islanding scheme of test system 1 with the proposed model

为作比较，图5和图6分别为文献[14]和文献[24]采用同样有功配置DG所获的孤岛划分方案，图中阴影节点为部分负荷恢复节点。

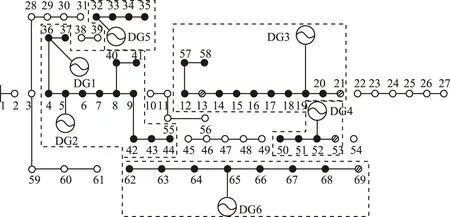
图5　文献[14]得到测试系统1的孤岛方案Fig.5　Islanding scheme of test system 1 with the model in ref[14]

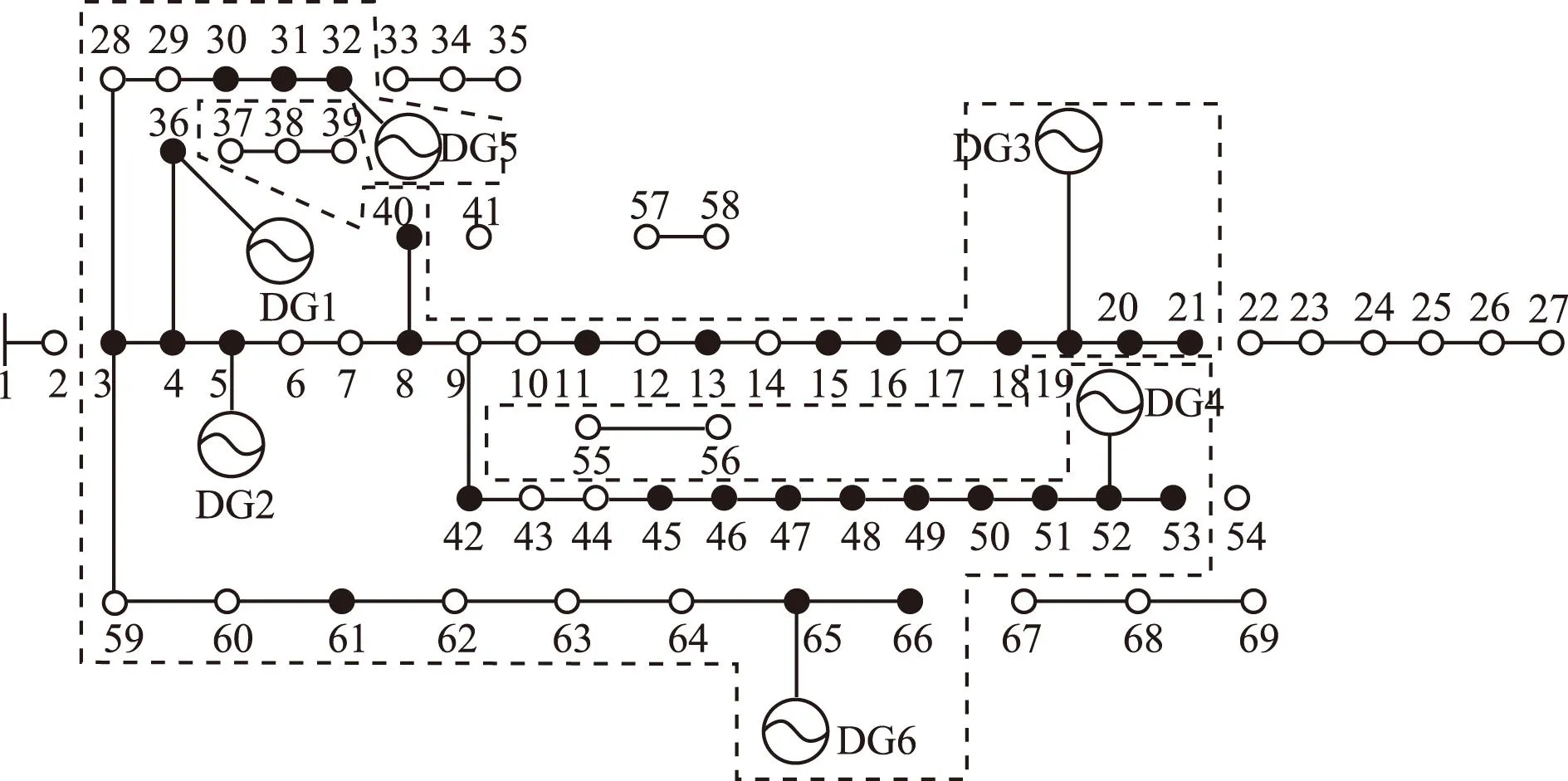
图6　文献[24]得到的约束孤岛划分Fig.6　Islanding scheme of test system 1 with the model in ref[24]

对比结果可知，本文所提模型得到孤岛方案切除负荷1 778.99 kW，较文献[14]方案的1 669.34 kW和文献[24]方案的1 669.84 kW多。这是因为文献[14]模型的负荷削减具有优先级可部分切除，而所提模型和文献[24]则是将负荷整体切除。更重要的是，本文所提模型考虑了DG的P-Q功率极限约束，在孤岛满足有功和无功功率平衡的前提下，还要求DG的功率输出满足自身功率特性，而非文献[14，24]简单对DG有功功率和无功功率完全解耦的处理。由于所提模型含DG功率特性约束方程，导致求解耗时12.53 s，较文献[24]的8.81 s长。

文献[24]用传统盒式约束方程式(71)替代功率极限线性化方程式(29)～式(34)，文献[24]和所提模型求得的DG运行点如图7所示。

(71)

由图7可见：①本文模型所求DG运行点，用*标识，均在P-Q功率极限内；②盒式约束模型求得的运行点，用o表示，DG1、DG2、DG5和DG6在P-Q功率极限外，这显然不符合工程实际。综上，DG功率盒式约束可能使DG运行点不可行。

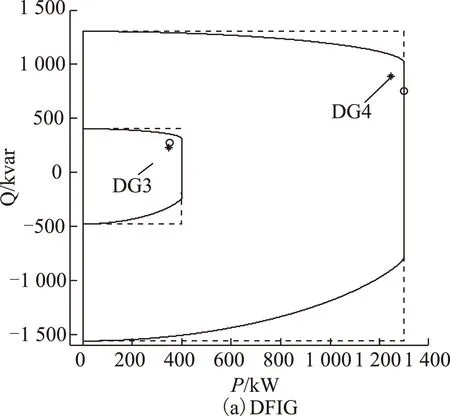
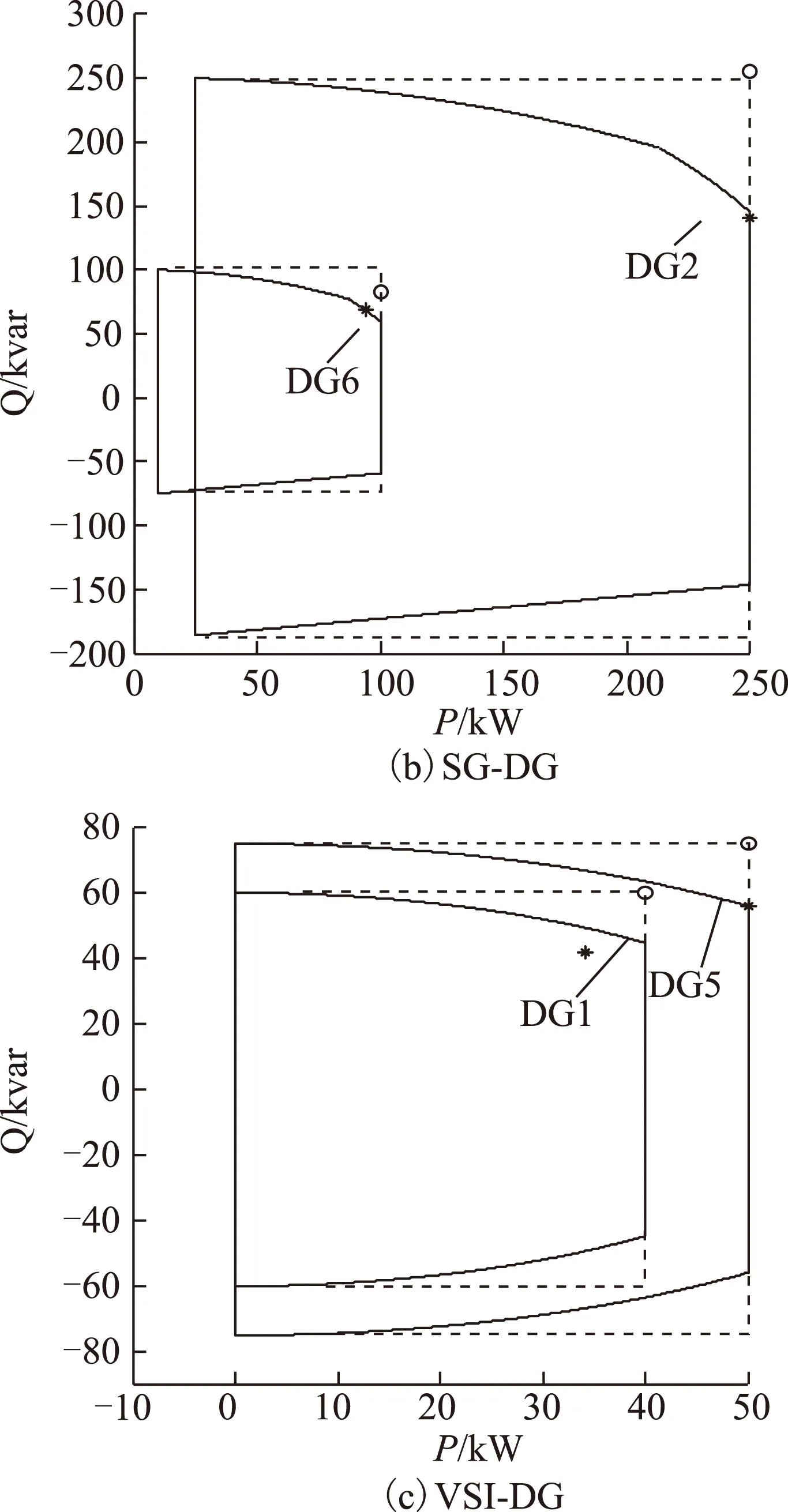
图7　测试系统1分布式电源运行点Fig.7　DG operating points in test system 1

为验证本文线性化模型所求孤岛的节点电压和支路电流误差情况，将孤岛中功率最大的DG作为松弛节点、其他DG作为恒功率节点，所获DG孤岛潮流解为基准，孤岛方案节点电压ΔV%和支路潮流ΔI%的相对误差如图8所示。图8显示，ΔV%和ΔI%平均相对误差为0.001%和0.102%，最大相对误差为0.008%和0.664%，可见本文所提模型准确度良好。

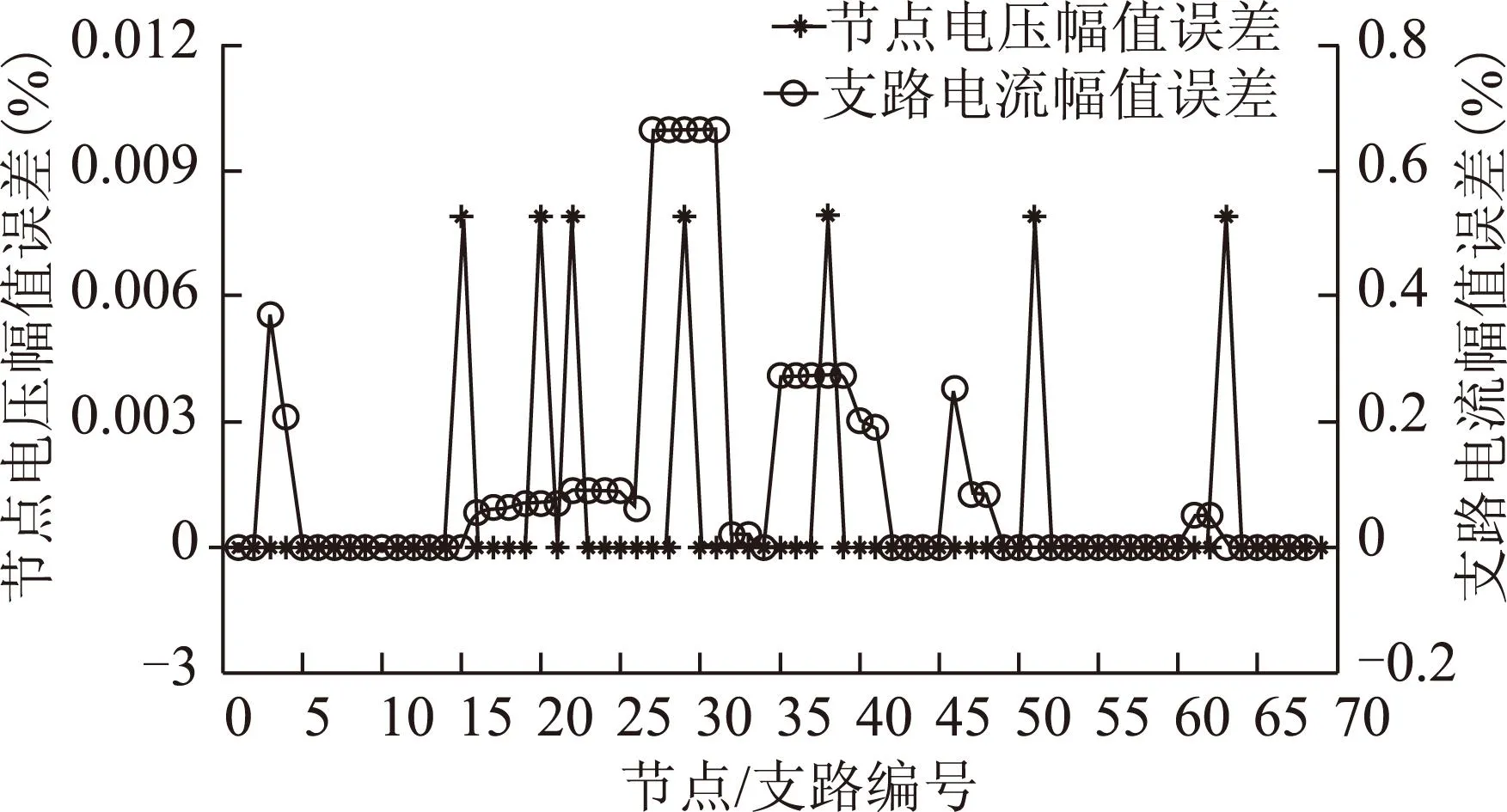
图8　测试系统1潮流解相对误差Fig.8　Relative error of power flow solution in test system 1

为进一步验证本文所提模型的适应性，以123节点配电系统[27]为基础搭建算例测试系统2，不同类型的DG按附表4～附表6接入系统。设支路1-117发生三相永久短路故障，故障期间负荷、DFIG和光伏出力的波动情况如图9所示。故障隔离后下游负荷节点失电，基于所提模型和文献[24]分别作孤岛划分，计算获得结果分别绘于图10和图11，结果比较见表2。

图9　负荷、双馈风力发电机与光伏出力Fig.9　Load power，DFIG and PV output

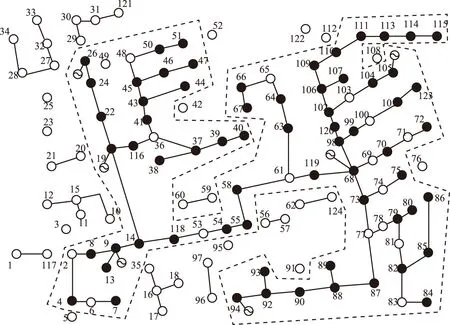
图10　测试系统2孤岛划分Fig.10　Islanding scheme of test system 2 with the proposed model

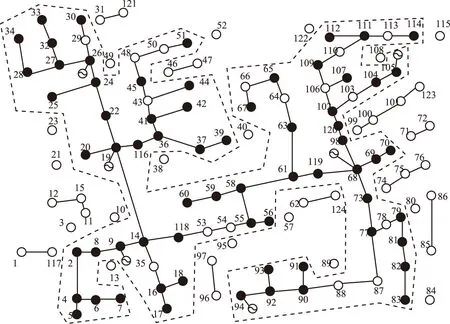
图11　文献[24]得到的约束孤岛划分Fig.11　Islanding scheme of test system 2 with the model in ref[24]

DG约束负荷切除/kWVmaxr/kVVminr/kVVmaxi/kVVmini/kV所提模型1374.907.0036.848-0.119-0.284文献[24]模型1388.087.0036.602-0.122-0.386

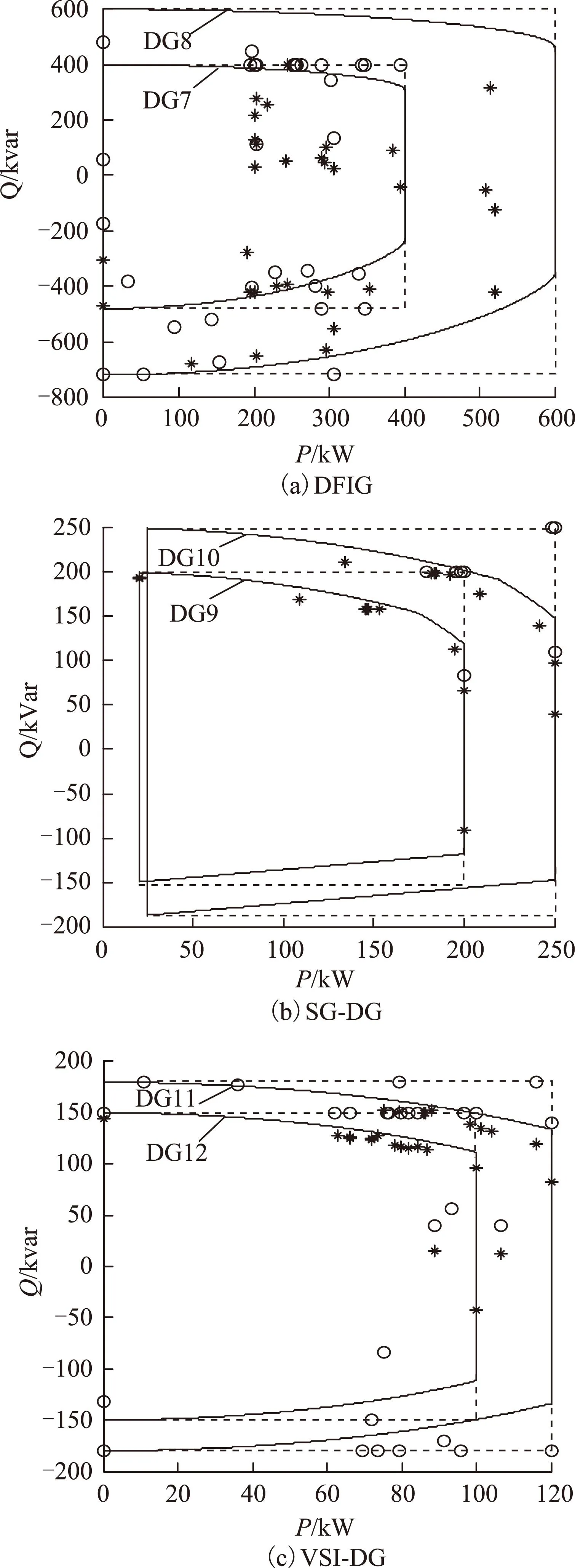
图12　测试系统2分布式电源运行点 功率特性曲线； 盒式约束曲线； 所提模型DG运行点； 盒式约束模型DG运行点Fig.12　DG operating points in test system 2

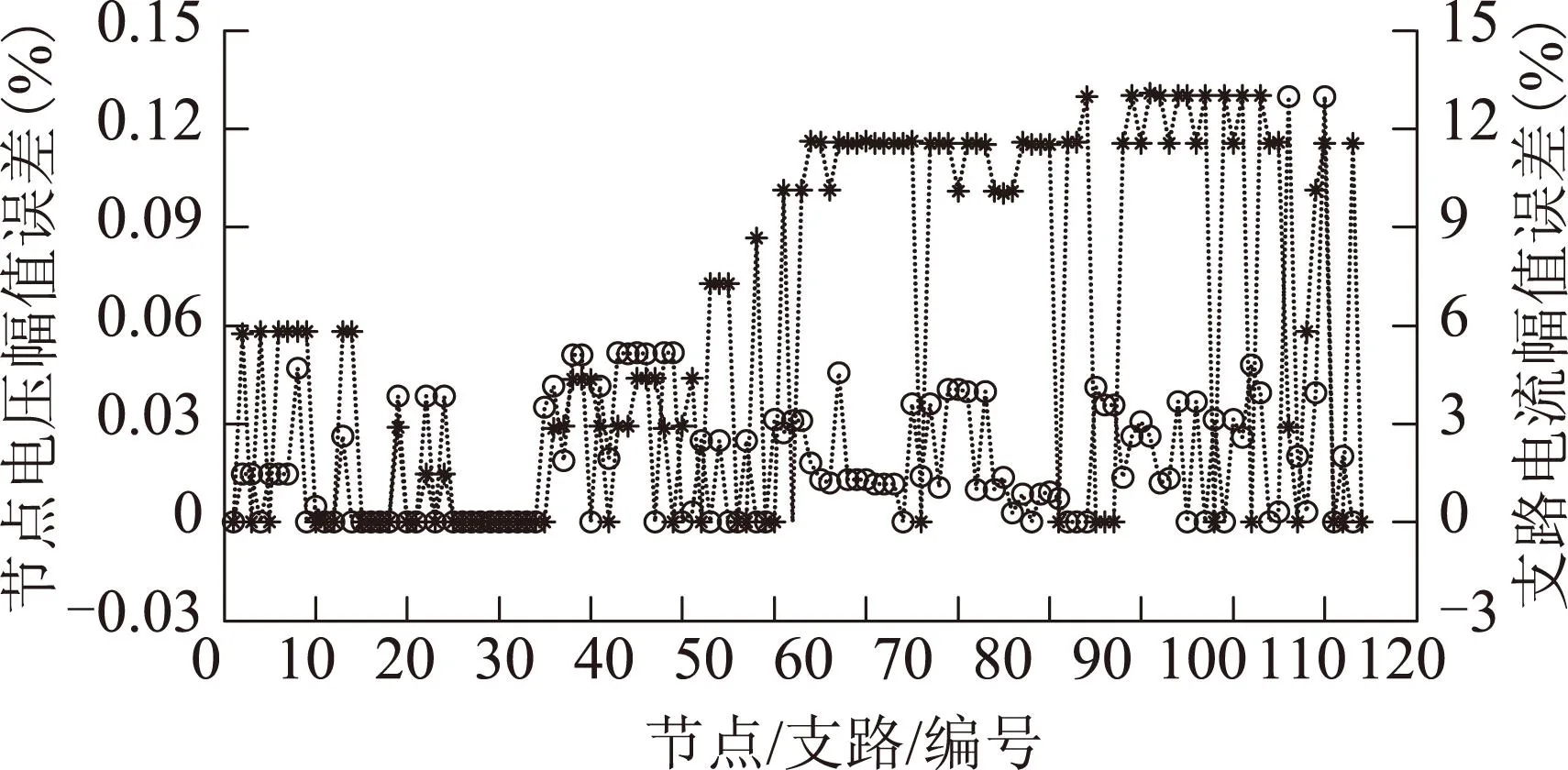
图13　故障恢复时刻测试系统2潮流解相对误差 节点电压幅值误差; 支路电流幅值误差Fig.13　Relative error of power flow solution in test system 2 at restoration time

与文献[24]模型相比较，所提模型考虑了DG功率特性，两者所得孤岛方案的节点电压偏差不大。将所提模型和文献[24]模型所获运行点绘于图12，故障恢复时刻孤岛节点电压ΔV%和支路潮流ΔI%的相对误差如图13所示。由图12和图13可见：本文模型所得运行点均在P-Q功率极限内，盒式约束将导致相当一部分DG运行点落在P-Q功率极限外，造成孤岛方案不可行；ΔV%和ΔI%平均相对误差为0.09%和2.90%，最大相对误差为0.13%和12.98%。造成支路电流误差大的原因在于该支路两侧潮流基值很小且其两侧节点电压虚部误差在孤岛内最大。同时还注意到，仅有两条支路误差较大，其他支路误差均小于5.20%。因此，本文所提模型具有较强的适应性，误差在可接受范围内。

本文所提模型考虑了DG的P-Q功率极限，其核心在于解析几何线性化模型。为进一步量化盒式约束模型和所提线性化模型的DG运行点覆盖情况，以VSI-DG为例，设电压幅值为1.0 (pu)，以功率极限围成的面积为基准值，求各模型围成面积对基准面积的覆盖情况。为此，定义DG运行点可行域覆盖率Rc为

(73)

式中，SM和SR分别为模型围成面积和基准面积。将不同模型对Rc的影响如图14所示。

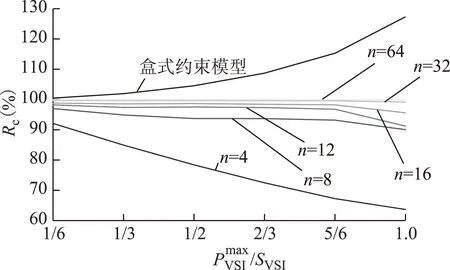
图14　分布式电源运行点可行域覆盖率Fig.14　Coverage rate of DG operating points feasible region

为量化分析分段数n的影响，在PG&E69系统的基础上仅节点65配置DG13形成测试系统3，DG具体参数如附表7所示，设支路63-64发生三相永久短路故障，故障隔离后故障点下游系统断电，形成如图15所示的孤岛。CPU时间和DG出力随P-Q功率极限曲线内接多边形分段数n的变化见表3。

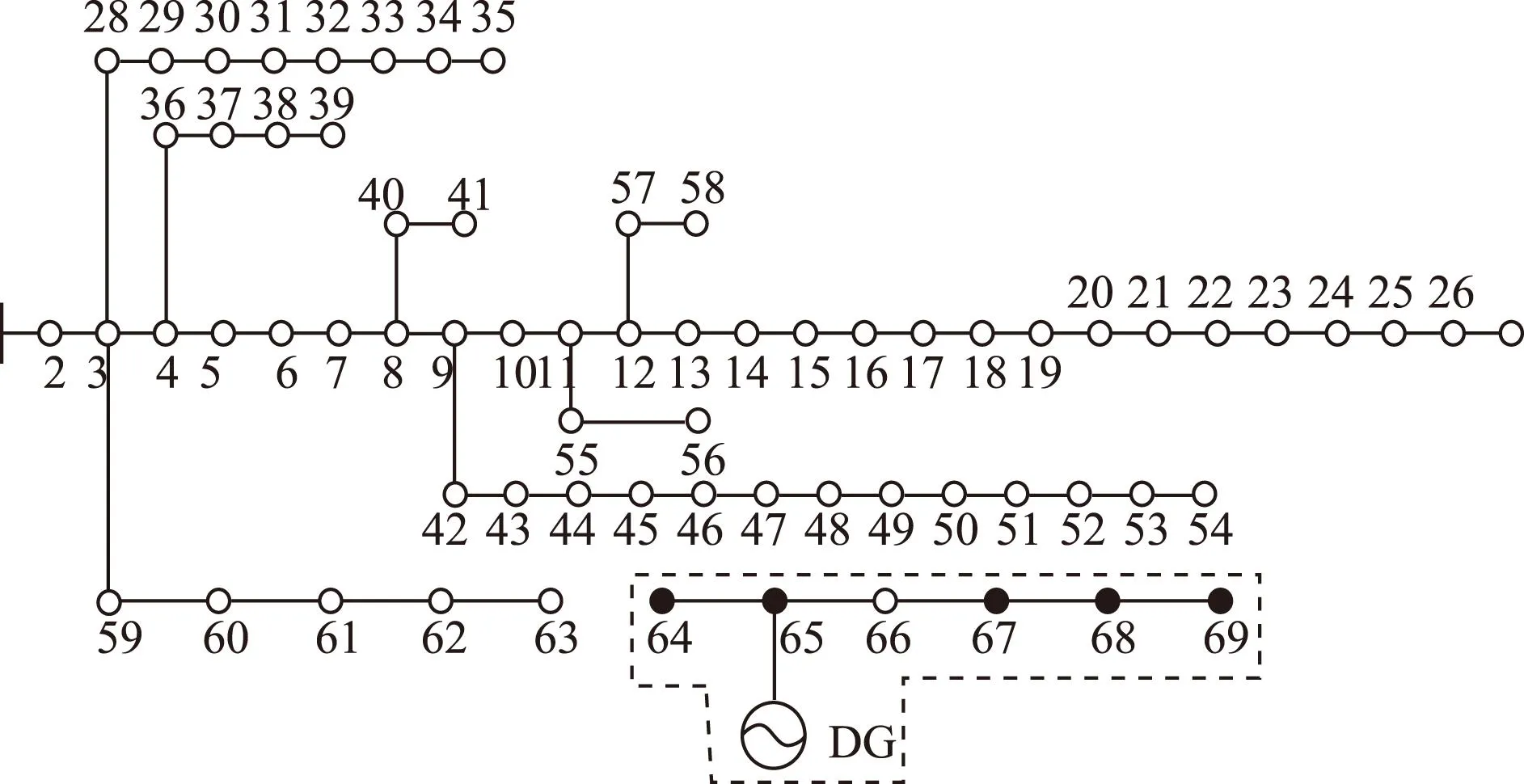
图15　测试系统3的孤岛划分方案Fig.15　Islanding scheme of test system 3

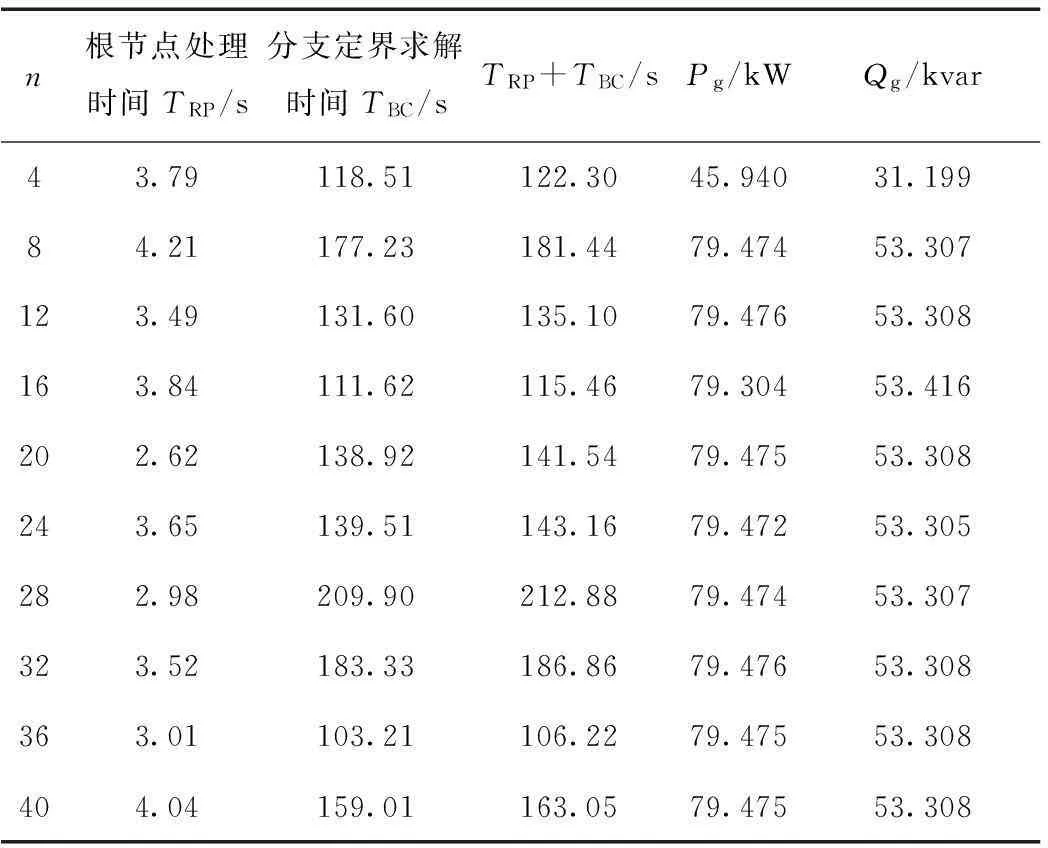
n根节点处理时间TRP/s分支定界求解时间TBC/sTRP+TBC/sPg/kWQg/kvar43.79118.51122.3045.94031.19984.21177.23181.4479.47453.307123.49131.60135.1079.47653.308163.84111.62115.4679.30453.416202.62138.92141.5479.47553.308243.65139.51143.1679.47253.305282.98209.90212.8879.47453.307323.52183.33186.8679.47653.308363.01103.21106.2279.47553.308404.04159.01163.0579.47553.308

分析表3可知：所提模型求解的CPU时间集中于分支定界求解时间，与分段数n无单调关系；当n=4时，有功出力为45.940 kW，较近似最优解79.475 kW的相对误差高达42.2%；为获得较高准确度的孤岛方案，推荐取内接正多边形分段数大于等于12。

4　结论

本文构建了一种主动配电网孤岛划分的混合整数规划模型，能有效计及DFIG、SG-DG和VSI-DG的功率特性，主要结论如下：①所提模型求解准确度高、适应性好，DG运行点满足其功率特性要求，符合工程实际；②合理化分段数取值是保证孤岛方案可行性和模型求解准确度的关键，推荐取分段数大于等于12，但其与求解CPU时间无单调关系。

后续研究将进一步拓展所提模型的应用范围，如主动配电网DG规划、网架规划及一体化规划等。

附录

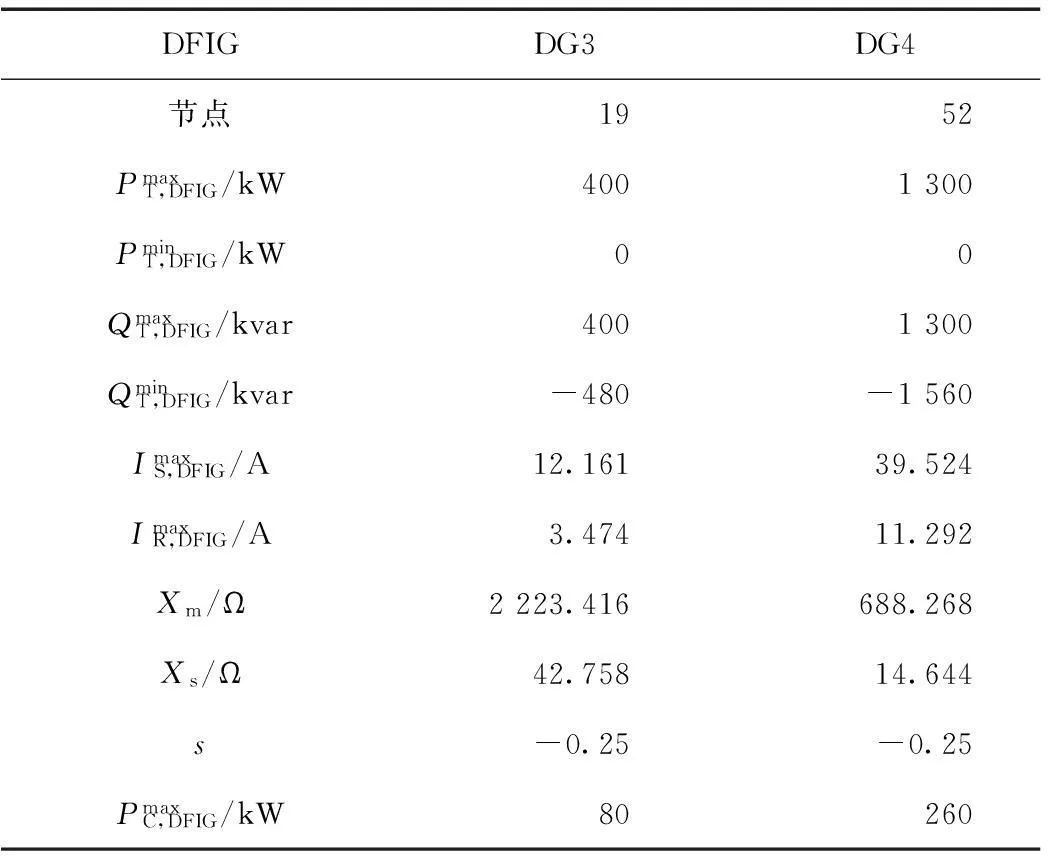
附表1　测试系统1双馈式感应风力发电机参数App.Tab.1　Parameters of doubly fed induction-based wind generator of test system 1

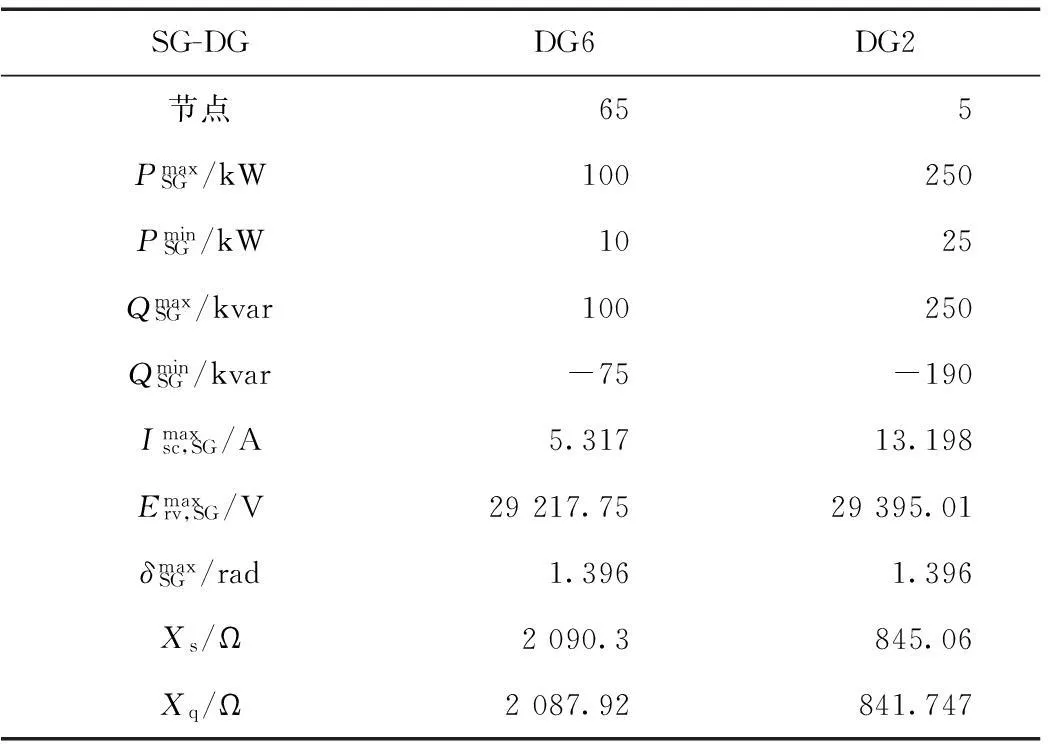
附表2　测试系统1同步发电机参数App.Tab.2　Parameters of synchronous generator of test system 1

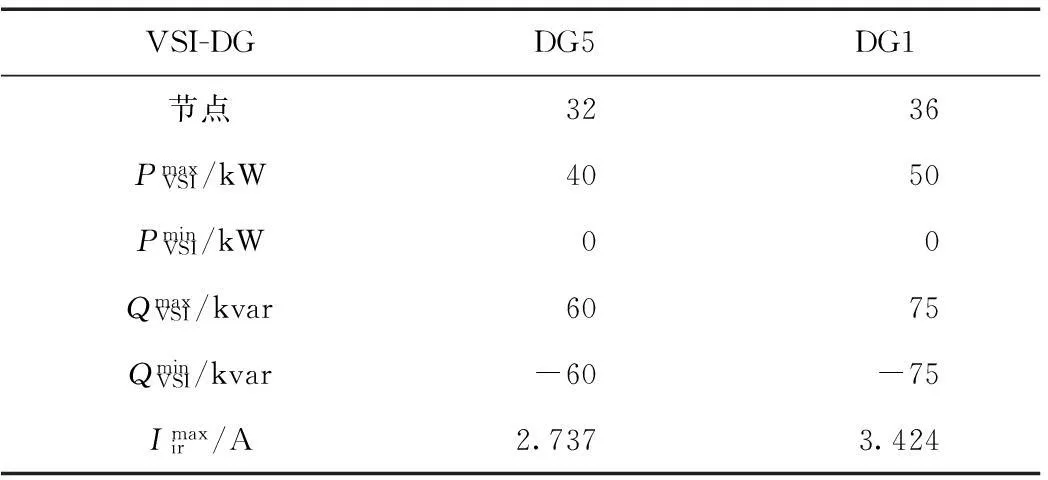
附表3　测试系统1逆变器接入型机组参数App.Tab.3　Parameters of voltage source inverter-based generator of test system 1

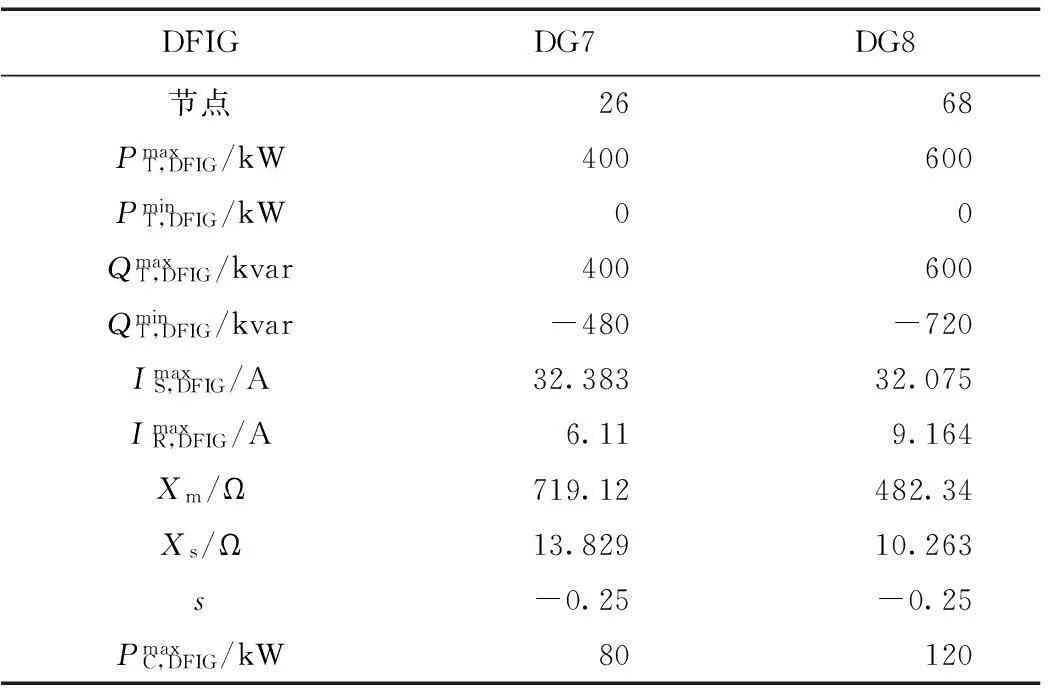
附表4　测试系统2双馈式感应风力发电机参数App.Tab.4　Parameters of doubly fed induction-based wind generator of test system 2

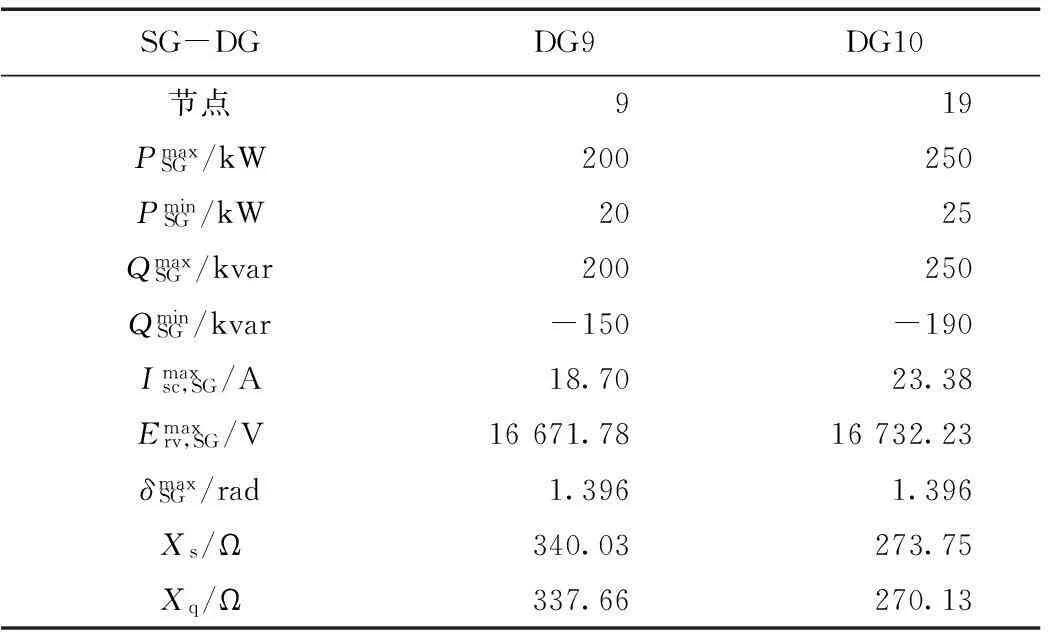
附表5　测试系统2同步发电机参数App.Tab.5　Parameters of synchronous generator of test system 2

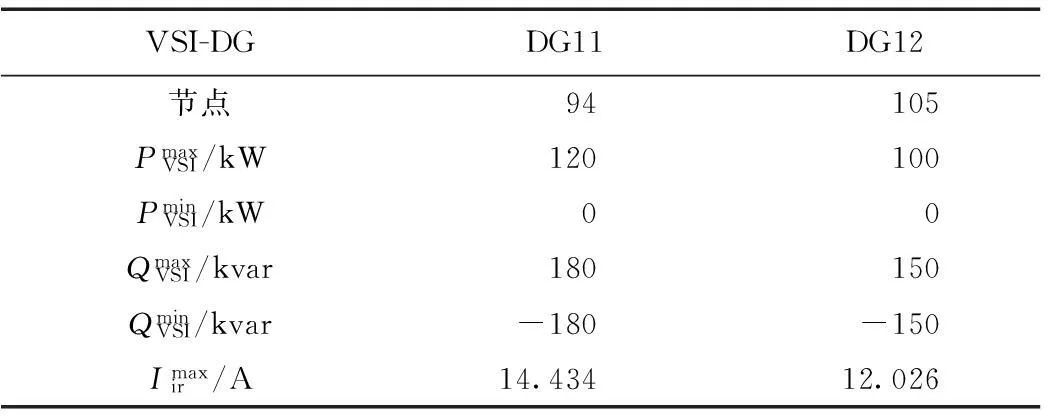
附表6　测试系统2逆变器接入型机组参数App.Tab.6　Parameters of voltage source inverter-based generator of test system 2

附表7　测试系统3逆变器接入型机组参数App.Tab.7　Parameters of voltage source inverter-based generator of test system 3

[1]沈鑫，曹敏.分布式电源并网对于配电网的影响研究[J].电工技术学报，2015，30(增1)：346-351.

Shen Xin，Cao Min.Research on the influence of distributed power grid for distribution network[J].Transactions of China Electrotechnical Society，2015，30(S1)：346-351.

[2]Coster E J，Myrzik J M，Kruimer B，et al.Integration issues of distributed generation in distribution grids[J].Proceedings of the IEEE，2011，99(1)：28-39.

[3]潘超，焦薇羽，孟涛，等.基于混合智能粒子群算法的广义电源主动配电网优化配置[J].电力系统保护与控制，2016，44(7)：69-75.

Pan Chao，Jiao Weiyu，Meng Tao，et al.Optimal allocation of generalized power sources in active distribution network based on hybrid intelligent particle swarm optimization algorithm[J].Power System Protection and Control，2016，44(7)：69-75.

[4]张跃，杨汾艳，曾杰，等.主动配电网的分布式电源优化规划方案研究[J].电力系统保护与控制，2015，43(15)：67-72.

Zhang Yue，Yang Fenyan，Zeng Jie，et al.Research of distributed generation optimization planning for active distributed network[J].Power System Protection and Control，2015，43(15)：67-72.

[5]IEEE Std 1547.2-2008.Application Guide for IEEE 1547 Standard for Interconnecting Distributed Resources with Electric Power Systems[S].2008.

[6]Mcdonald J.Adaptive intelligent power systems：active distribution networks[J].Energy Policy，2008，36(12)：4346- 4351.

[7]张建华，曾博，张玉莹，等.主动配电网规划关键问题与研究展望[J].电工技术学报，2014，29(2)：13-23.

Zhang Jianhua，Zeng Bo，Zhang Yuying，et al.Key issues and research prospects of active distribution network planning[J].Transactions of China Electrotechnical Society，2014，29(2)：13-23.

[8]Bae I S，Kim J O.Reliability evaluation of customers in a microgrid[J].IEEE Transactions on Power Systems，2008，23(3)：1416-1422.

[9]刘传铨，张焰.计及分布式电源的配电网供电可靠性[J].电力系统自动化，2007，31(22)：46- 49.Liu Chuanquan，Zhang Yan.Distribution network reliability considering distribution generation[J].Automation of Electric Power Systems，2007，31(22)：46- 49.

[10]王昌照.含分布式电源配电网故障恢复与可靠性评估研究[D].广州：华南理工大学，2015.

[11]汪隆君，王钢，张竣淇，等.基于混合决策图的分布式电源配电系统故障恢复方法：中国，201310487810.X[P].2014-2-12.

[12]丁磊，潘贞存，丛伟.基于有根树的分布式发电孤岛搜索[J].中国电机工程学报，2008，28(25)：62-67.

Ding Lei，Pan Zhencun，Cong Wei.Searching for intention islanding strategies of distributed generation based on root tree[J].Proceedings of the CSEE，2008，28(25)：62-67.

[13]董晓峰，陆于平.基于改进Prim算法的分布式发电孤岛划分方法[J].电网技术，2010，34(9)：195-201.

Dong Xiaofeng，Lu Yuping.Islanding algorithm for distributed generators based on improved Prim algorithm[J].Power System Technology，2010，34(9)：195-201.

[14]王旭东，林济铿.基于分支定界的含分布式发电配网孤岛划分[J].中国电机工程学报，2011，31(7)：16-20.

Wang Xudong，Lin Jikeng.Island partition of the distribution system with distributed generation based on branch and bound algorithm[J].Proceedings of the CSEE，2011，31(7)：16-20.

[15]李振坤，周伟杰，钱啸，等.有源配电网孤岛恢复供电及黑启动策略研究[J].电工技术学报，2015，30(21)：67-75.Li Zhenkun，Zhou Weijie，Qian Xiao，et al.Distribution network restoration and black start based on distributed generators[J].Transactions of China Electrotechnical Society，2015，30(21)：67-75.

[16]靳小龙，穆云飞，贾宏杰，等.面向最大供电能力提升的配电网主动重构策略[J].电工技术学报，2014，29(12)：137-147.

Jin Xiaolong，Mu Yunfei，Jia Hongjie，et al.An active reconfiguration strategy for distribution network based on maximum power supply capability[J].Transactions of China Electrotechnical Society，2014，29(12)：137-147.

[17]李振坤，刘俊，杨帆，等.有源配电网的综合供电恢复及改进遗传算法[J].电力系统保护与控制，2014，42(17)：24-30.

Li Zhenkun，Liu Jun，Yang Fan，et al.Restoration of distribution network containing DG and a refined genetic algorithm[J].Power System Protection and Control，2014，42(17)：24-30.

[18]李滨，祝靖，李佩杰，等.含非可靠分布式电源的配电网孤岛划分[J].电力系统自动化，2015，39(8)：59-65.

Li Bin，Zhu Jing，Li Peijie，et al.Island partition of distribution network with unreliable distributed generators[J].Automation of Electric Power Systems，2015，39(8)：59-65.

[19]胡哲晟，郭瑞鹏，蓝海波，等.基于有向图的含分布式电源配电网孤岛划分模型[J].电力系统自动化，2015，39(14)：97-104.

Hu Zhesheng，Guo Ruipeng，Lan Haibo，et al.Islanding model of distribution systems with distributed generators based on directed graph[J].Automation of Electric Power Systems，2015，39(14)：97-104.

[20]Trodden P A，Bukhsh W A，Grothey A A，et al.Optimization-based islanding of power networks using piecewise linear AC power flow[J].IEEE Transactions on Power Systems，2014，29(3)：1212-1220.

[21]张丽，徐玉琴，王增平，等.包含分布式电源的配电网无功优化[J].电工技术学报，2011，26(3)：168-174.

Zhang Li，Xu Yuqin，Wang Zengping，et al.Reactive power optimization for distribution system with distributed generators[J].Transactions of China Electrotechnical Society，2011，26(3)：168-174.

[22]Lof P A，Andersson G，Hill D J.Voltage dependent reactive power limits for voltage stability studies[J].IEEE Transactions on Power Systems，1995，10(1)：220-228.

[23]Borghetti A.A mixed-integer linear programming approach for the computation of the minimum-loss radial configuration of electrical distribution networks[J].IEEE Transactions on Power Systems，2012，27(3)：1264-1273.

[24]Ferreira R S，Borges C L T，Pereira M V F.A flexible mixed-integer linear programming approach to the AC optimal power flow in distribution systems[J].IEEE Transactions on Power Systems，2014，29(5)：2447-2459.

[25]Geiβler B，Martin A，Morsi A，et al.Using piecewise linear functions for solving MINLPs[J].Mixed Integer Nonlinear Programming，2012，154：287-314.

[26]Baran M E，Wu F F.Optimal capacitor placement on radial distribution system[J].IEEE Transactions on Power Delivery，1989，4(1)：725-734.

[27]Kersting W H.Radial distribution test feeders[J].IEEE Transactions on Power Systems，1991，6(3)：975-985.

A Mixed Integer Programming Model for Islanding Partition of Active Distribution Network

Wang LongjunGuo JunhongWang GangZhong Qing

(School of Electrical PowerSouth China University of TechnologyGuangzhou510640China)

Reactive power balance is an important factor restricting the feasibility and safety of islanding.As the main reactive power source of the active distribution network，the power characteristics of the distributed generation (DG) are often neglected so that it is difficult to satisfy the power balance of islands.In order to conciliate accuracy and computational performance，a mixed integer programming model for islanding partition of the active distribution network is established.TheP-Qcapability limits of DGs are linearized based on the analytic geometry model，which can consider the power characteristics of the doubly-fed wind generator，the synchronous generator，and the voltage source inverter-based generator.The product terms between the voltage and the power in the Kirchhoff’s current equations are linearized using the bi-linear model.The separation model is used for solving the variations of the islanding network topology and the load shedding problems.The square terms are linearized by adopting the special ordered sets-2.The numerical results of case studies demonstrate that the proposed model is of high accuracy and good adaptability；and DG’s operation satisfies its power characteristics and practical engineering.Furthermore，the rationalizing segmentation is the key to the feasibility of the island scheme and the solution of proposed model，whose recommended value is more than 12.But there is no monotonous relationship between segments and CPU time.

Active distribution network，islanding partition，distributed generation，mixed integer programming，analytic geometry，bi-linear model

2015-08-02改稿日期2016-02-27

TM727

汪隆君男，1982年生，博士，讲师，研究方向为电力系统规划与可靠性。

E-mail：wlj_scut@126.com(通信作者)

郭俊宏男，1991年生，硕士研究生，研究方向为电力系统规划与可靠性。

E-mail：gjh_91@163.com

国家自然科学基金(51307063)和教育部高等学校博士学科点专项科研基金(20120172120042)资助项目。