有限阶正则广义分布参数系统的扰动脉冲能观性

夏恩惠（西安交通大学，运筹学与控制论，陕西西安710049）

有限阶正则广义分布参数系统的扰动脉冲能观性

夏恩惠
（西安交通大学，运筹学与控制论，陕西西安710049）

本文研究的是带有扰动项v的正则广义分布参数系统E x⋅=Ax+Gu+Hv 。首先，我们在原有给出了的带有扰动项的正则广义分布参数系统的分布解基础上，对其分布解分类加以研究。再者，本文结合有限阶正则广义分布参数系统的扰动脉冲能控性的研究，给出了有限阶正则广义分布参数系统的扰动脉冲能观性的定义。最后，我们给出了有限阶正则广义分布参数系统是否为扰动脉冲能观的重要判断依据，并且通过建立对偶系统，分析得出原系统与其对偶系统之间关于扰动脉冲能控能观性的联系。本文所得结果对于研究广义分布参数系统的设计问题有重要的理论与应用价值。

正则广义分布参数系统；脉冲能观性；扰动脉冲能观性

本文引用格式：夏恩惠.有限阶正则广义分布参数系统的扰动脉冲能观性［J］.新型工业化，2016，6（7）：40-45.

0　引言

近年来，随着人工智能的不断发展，现代控制理论中很多有限维的系统理论已经不足以解决大数据时代的很多系统控制了。因此，很多学者也在研究分布参数系统相关理论，并得出了很多重要结论，包括带有扰动项的有限维系统的脉冲能控能观性研究以及无穷维广义正则分布参数系统的脉冲能控能观性结论。但是到目前为止，对于无穷维广义正则分布参数系统，还没有人研究带有扰动项后该系统的相关性质会发生什么样的变化。故本文就将对此问题进行分析和研究。

为了研究广义正则分布参数系统的扰动脉冲能控能观性，可以把所要研究的部分分为四大板块：有限阶广义正则分布参数系统的扰动脉冲能控性、有限阶广义正则分布参数系统的扰动脉冲能观性、无限阶广义正则分布参数系统的扰动脉冲能控性以及无限阶广义正则分布参数系统的扰动脉冲能观性。其中有限阶广义正则分布参数系统的扰动脉冲能控性已经在另一篇我的文章中分析过了，本文就有限阶广义正则分布参数系统的扰动脉冲能观性进行分析和研究。另外两个部分是关于无限阶的系统会在今后继续研究。

为了减弱干扰项对分布参数系统的干扰程度以达到系统的控制效果，一些H∞控制问题已经得到了不少学者的关注［1］-［7］。在这些研究领域中，研究的带有控制输入u和干扰项v的分布参数系统形式如下：

其中x是系统状态。E是方阵可能是奇异的。但目前大部分学者的研究都是基于有限维的分布参数系统。下面我们来介绍本文所要研究的正则广义分布参数系统的定义。

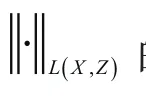
1　有限阶正则广义分布参数系统

形式如下：

其中E∈L（X，Z），A∈CD（X，Z），B ∈L（U，Z）；x（t）∈X，u（t）∈U分别表示状态向量和输入向量。我们定义广义分布参数系统的有限阶正则性如下：

定义1 对于广义分布参数系统（1），如果存在Banach空间X1， X2及单射P∈L（Z，X1×X2），双射Q∈L（X1×X2，X），使得

其中N是一个h阶幂零算子（即存在正整数h使得Nh-1≠0，Nh=0），K是强连续算子半群的生成元，则称原系统（1）是阶数为h的正则广义分布参数系统，简称为有限阶正则广义分布参数系统。

此时，算子P，Q把系统（1）变换为Banach空间X1×X2上如下形式的解耦系统

由（2.1）-（2.2）所表示的系统称为有限阶正则广义分布参数系统的正则标准形式。

通过之前的学习，我们已经知道给定阶数h和初值的系统（2.1）和（2.2），当系统的输入向量u（t）为任意h阶连续可导向量时，有限阶正则广义分布参数系统的解已经给出。并且，我们知道有限阶正则广义系统（1）的脉冲能控性是只和其快子系统（2.2）有关的。那么当输入向量u（t）为分段光滑的时候，原系统的解又将如何。接下来，我们只对其快子系统进行研究。

设计与研究

2　初始值问题的分布解

快子系统

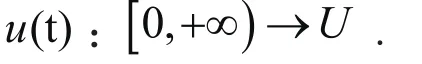
在研究初值问题分布解之前，我们先作一些相关定义。

2.1相关定义

2.2分段光滑函数映射的拉普拉斯变换

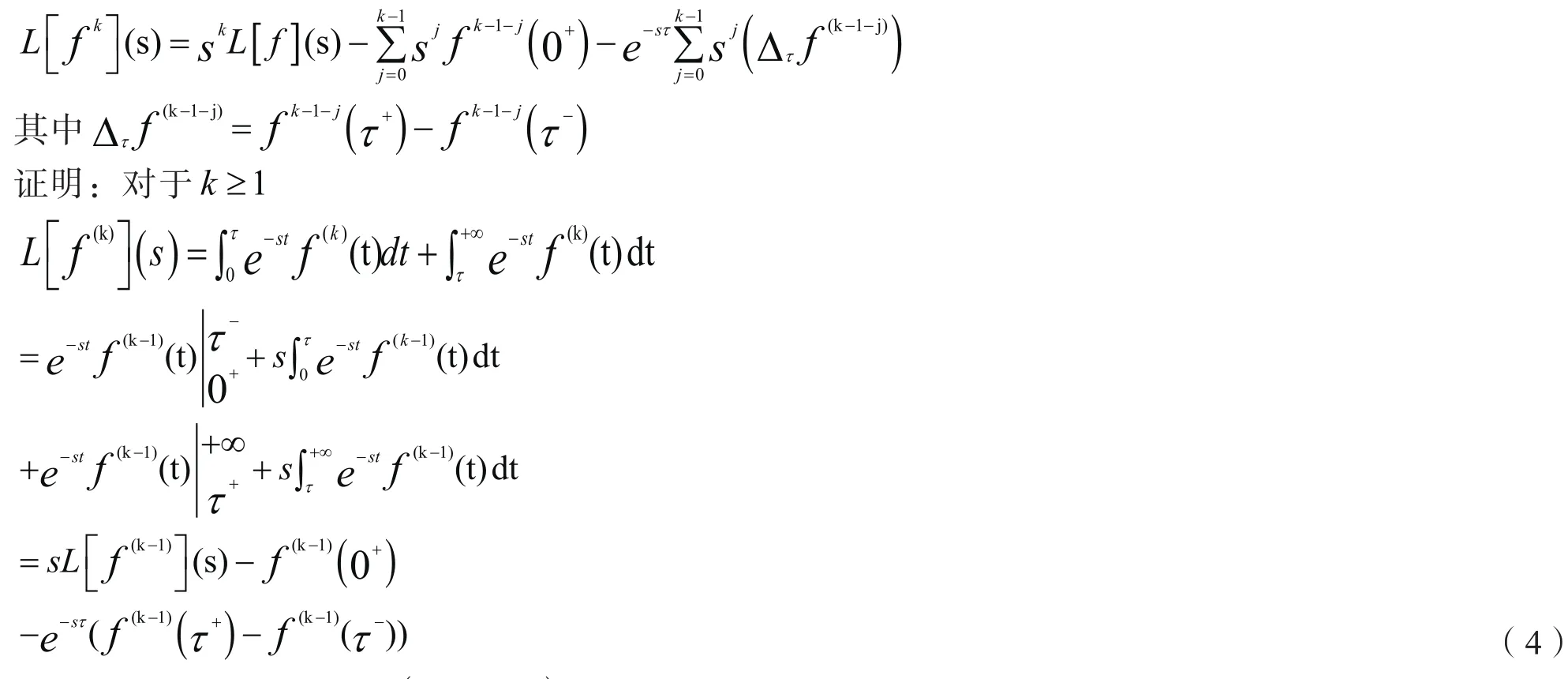
2.3初始值问题的分布解

现在我们来考虑初始值问题（3）。它的频域形式为：

（sN- I）X（s）=Nx0+BU（s）（5）

很显然，我们得到：

下面的引理向我们展示了输入向量的节点以及它的导数对频域解得影响。

证明：为了简单，我们只证明u只存在一个间断点τ＞0的情况。由推论1知：

交换连加号顺序，注意Nq=0，我们得到

将上式代入（7）中并推广至无穷个间断点时则得出结论。

定义4：用逆拉普拉斯变换从（5）中解出的X（s）称为（3）的分布解。

定理1：u∈κh

P（R+，LP（U））带有间断点0＜τ1＜τ2＜…。那么系统（3）的分布解为：

3　脉冲的分类

在上述的状态响应中出现两种类型的脉冲，第一种脉冲表达式是：

第一种脉冲由初始值和输入引起。第二种脉冲表达式是：

第二种脉冲是由输入向量u的跳跃Δτu（l），l= 0，1，…，q -1和u在τ＞0的导数引起的。第二种脉冲与初值无关。我们需要强调的是这两种脉冲有着本质的不同。

4　扰动脉冲能观性

4.1扰动脉冲能观性

研究系统：

因为本文下面考虑的是由输出来观测状态响应，这和输入向量u（t）和扰动向量v（t）没有关系。因此，本文下面主要研究系统：

定义5：系统（11）中，若由y（0）=0都能推出x（t）|t=0=0，则系统（11）是扰动脉冲能观的。

定理：2：系统（11）扰动脉冲能观当且仅当ker（Q［C1，N］N）∩ker（Q［C2，N］N）=kerN.

因此要由y（0）=0推出xI（t）|t =0=0，当且仅当ker（Q［ C1，N］N）∩ker（Q［ C2，N］N）=kerN .

综上，由定义5知，系统（11）扰动脉冲能观当且仅当ker（Q［ C1，N］N）∩ker（Q［ C2，N］N）=kerN

定理3：一般系统：

E x⋅=Ax+Gu+Hv

y（t）=Mx（t）

如上的一般系统，它的慢子系统状态响应中不含脉冲项，因此一般系统的慢子系统均是扰动脉冲能观的。因此一般系统的扰动脉冲能观性等价于其快子系统的能观性。

4.2例子

因为

5　对偶原理

本文的对偶原理揭示的是无穷维有限阶正则广义分布参数系统的扰动脉冲能控性和其对偶系统的扰动能观性之间的联系。 下面X，Y，U，V，Z均在Hilbert空间上研究。

下面只考虑快子系统。

定义6：系统（10）的对偶系统定义如下：定理4：当ker（Q［ C1，N］N），ker（Q［ C2，N］N），kerN，kerN*是闭的且kerN*=ran（N*C（N*，C1*））系统（10）扰动脉冲能观则其对偶系统（13）扰动脉冲能控。

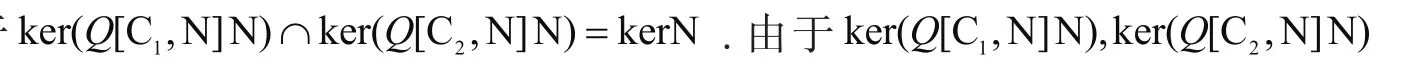
kerN，kerN*均是闭的。故：

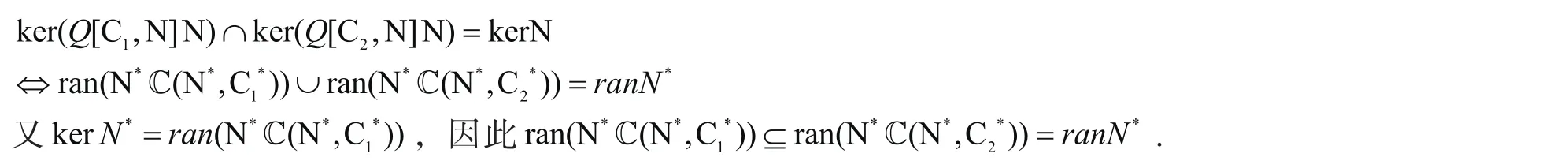
因此根据之前研究无穷维有限阶正则广义分布参数系统扰动脉冲能控性［8］充要条件得系统（13）扰动脉冲能控。

［1］Zhibin Yan.“Disturbance impulse controllability in Descriptor system”，IEEE Trans.Autom.Control，2011.

［2］Ge，Zhaoqiang.“Impulse observability and impulse controllability of regular degenerate evolution systems.” Journal of Systems Science ＆ Complexity ：1-13.

［3］I.Masubuchi，Y.Kamitane，A.Ohara，and N.Suda，“H∞control for descriptor systems：A matrix inequalities approach，” Automatica，1997，33（4）：669-673.

［4］曾丽琼，匡洪海，张曙云，等.风电并网前后的系统短路故障特性分析与仿真［J］.新型工业化，2016，6（4）：27-33.ZENG Li-qiong，KUANG Hong-hai，ZHANG Shu-yun，et al.Research on the Influence of Wind Power Integration by Matlab for System Dynamic Stability［J］.The Journal of New Industrialization，2016，6（4）：27-33.

［5］I.Masubuchi，“Dissipativity inequalities for continuous-time descriptor systems with applications to synthesis of control gains，” Syst.Control Lett.，2006，55（2）：158-164.

［6］刘建国，刘振丙.基于一阶矩的DFT 脉动阵列快速实现［J］.新型工业化，2011，1（4）：8-15.Liu Jianguo，Liu Zhenbing.Efficient Systolic Implementation of DFT Using only the First-order Moments［J］.The Journal of New Industrialization，2011，1（4）：8-15.

［7］I.Masubuchi，“Output feedback controller synthesis for descriptor systems satisfying closed-loop dissipativity，” Automatica，2007，43（2）：339-345.

［8］H.S.Wang，C.F.Yung，F.R.Chang.“Bounded real lemma and H∞control for descriptor systems，” Proc.Inst.Elect.Eng.D，1998，145（3）：316-322.

［9］C.F.Yung.“H∞control for linear discrete-time systems：State feedback and full information cases，” in Proc.17thWorld Congress，IFAC，Seoul，Korea，Jul.6-11，2008，1003-10008.

［10］Y.Xia，E.K.Boukas，P.Shi，et al.“Stability and stabilization of continuous-time singular hybrid systems，” Automatica，2009，45（6）：1504-1509.

［11］任丽娜，吕明月，刘爽爽，等.基于蜂群算法优化的变桨距自抗扰控制器［J］.新型工业化，2014，4（6）：43-48.Ren Lina，Lv Mingyue，Liu Shuangshuang，et al.Based on colony optimization algorithm Pitch ADRC［J］.The Journal of New Industrialization，2014，4（6）：43-48.

Disturbance Impulse Observability of Infinite-dimensional Regular Descriptor System with Finite Order

XIA En-hui
（School of Operations research and control theory，University of Jiaotong University of Xi'an，Xi'an 710049，China）

Impulse observability of infinite-dimensional regular descriptor system with finite order E x⋅=Ax+Gu+Hv，which goes with external disturbance v is considered.Firstly，on the premise of infnite-dimensional descriptor system with external disturbance，we study on the distributional solution of the system.Secondly，combining with the theory about impulse controllability of infnite-dimensional regular descriptor system with fnite order，we give the defnition of disturbance impulse observability of infnite-dimensional regular descriptor system with fnite order.Finally，necessary and suffcient conditions for the disturbance impulse observability of the system are obtained，and through the establishment of the dual system，we get the analysis results of the original system and its dual system of between about disturbance impulsive controllability observability contact.The result plays a very important role in later research about infnite-dimensional regular descriptor system.

Infnite-dimensional regular descriptor system；Impulse observability；Disturbance impulse observability

10.19335/j.cnki.2095-6649.2016.07.007

XIA Enhui.Disturbance Impulse Observability of Infnite-dimensional Regular Descriptor System with Finite Order［J］.The Journal of New Industrialization，2016，6（7）：40-45.