一种两级式变换器的最优工作点分析
2016-08-29胡潇潇吴琨同济大学电子与信息工程学院上海201804
胡潇潇,吴琨(同济大学电子与信息工程学院,上海 201804)
一种两级式变换器的最优工作点分析
胡潇潇,吴琨
(同济大学电子与信息工程学院,上海 201804)
本文详细分析了一种两级式变换器的优化设计,针对谐振变换器级联Buck电路的结构,根据开关损耗和导通损耗,量化了变压器的匝比与效率之间的关系,理论计算出了该变换器的最优工作点。该两级式变换器适用于48V母线电压输入的VRM,解决了传统单级式变换器在此应用上出现的占空比失控和效率低等问题。此外,本文搭建了一台48V输入、5V/8A输出的原理样机验证了理论分析的正确性。
两级式变换器;最优工作点;开关损耗;导通损耗
本文引用格式:胡潇潇,吴琨.一种两级式变换器的最优工作点分析[J].新型工业化,2016,6(7):22-27.
0 引言
随着超大规模集成电路的飞速发展,计算机以及通讯设备对供电电源提出了越来越高的要求。Intel公司对VRM(Voltage Regulator Module)的输出电压、电流的需求[1]如下:输出电压越来越低(<1V),输出电流越来越大(>150A)。与此同时,要求输出电压在动态变化时电压波动量小(<2%oV)[1]。VRM向着低电压、大电流、高可靠性、高效率的方向发展[2-3]。
输入直流母线上的损耗会随负载功率的提高而相应增加。为减小直流母线上的损耗,VRM的输入电压由原先的5V提高到12V,以及未来将达到48V[4-6]。这使得输入电压与输出电压相差十分悬殊,不利于变换器的设计。文献[7]提出了采用电感带抽头的Buck变换器以扩展占空比,并结合多相交错并联技术,优化了VRM的设计。然而,带中间抽头的Buck变换器对占空比的扩展毕竟是有限的,当输入电压为24V以上时,其不再适用。文献[8]提出的磁集成推挽正激变换器可以通过调整变压器的匝比来实现占空比的扩展,倍流整流方式可以提高变换器的效率,磁集成技术则提高了功率密度。
当母线电压达到48V时,一般采用两级式结构代替传统的单级结构。由于谐振电路转换效率高、易于设计EMI并且便于实现软开关[9]等优点,常被用于两级式变换器的前级。具体地,可令谐振变换器的开关频率固定,通过控制后级来调节输出。
本文详细分析了一种两级式变换器的开关损耗和导通损耗,量化了变压器的匝比与效率之间的关系,理论计算出了该变换器的最优工作点。此外,本文搭建了一台48V输入、5V/8A输出的原理样机验证了理论分析的正确性。
1 两级式变换器的结构
两级式变换器由1个隔离型变换器级联1个Buck变换器[10]构成。隔离型变换器实现大幅降压功能,Buck变换器用于调节输出电压。
本文选择有源钳位正激谐振电路作为两级式变换器中的隔离变换器。即采用的两级式变换器的结构为“有源钳位正激谐振+Buck”(如图1)。

图1 两级式变换器Fig.1 Two-stage converter
有源钳位正激谐振电路是基于有源钳位正激电路上的谐振。有源钳位正激拓扑结构[11]与传统的单端正激变换器的拓扑结构基本相同,但通过增加辅助开关管和储能电容,就能解决变压器磁饱和的问题。在此优势的基础上,通过增加输入大电感、谐振电容,去除副边滤波电感和续流二极管,形成有源钳位正激谐振电路。利用谐振电路自身的结构特点[9],较容易实现软开关,已广泛应用于高效率和高功率密度的场合。然而,对谐振变换器而言,开关频率在谐振频率附近时工作状态最佳。调节开关频率会降低效率,同时开关频率的大范围变化会使得EMI和磁元件的设计难度加大。为解决上述问题,目前较多采用的方案是两级串联结构[12]。保持有源钳位正激谐振变换器的开关频率恒定,通过调节Buck电路的占空比来调节输出
2 变压器匝比n对两级式变换器效率的影响分析
如图1所示,Cr为谐振电容。T为有源钳位正激谐振电路的变压器,其励磁电感值为Lm,N1、N2为变压器T的原副边绕组,Lr为谐振电感与变压器T原边漏感之和。将开关管Q1、Q2和Q5的占空比设定为0.5,且开关频率恒定。开关管Q3和Q4占空比可调,且Q3和Q4的占空比互补。
为简化电路分析,下文的描述主要针对稳态工作的情况,并建立在如下假设之上:
1)输入电感足够大,可认为输入是一个电流源。
2)输出电容足够大,可认为输出电压恒为Vo。
3)变压器T的原副边匝比n=N1/N2。
有源钳位正激谐振电路的输出电压V1由变压器T的匝比n决定,输出电压V1的大小又影响着Buck电路的占空比D2,从而影响两级式变换器的效率。
由于有源钳位正激谐振的输出电压V1与匝比n之间无法用具体公式表达,但其之间有一一对应的关系。通过改变变压器匝比n,借助中间电压V1从而量化出各开关管的开关损耗和导通损耗之和与Buck电路的占空比D2的数量关系,从而分析出该两级式变换器的最佳工作点,使得该变换器效率最高。
(1)开关损耗
因为有源钳位正激谐振电路的开关管都是零电流开通和关断,所以开关损耗为0。开关损耗主要体现在Buck电路上。
由于Buck电路采用同步整流技术,开关损耗主要在主开关管Q3上。其计算公式为:
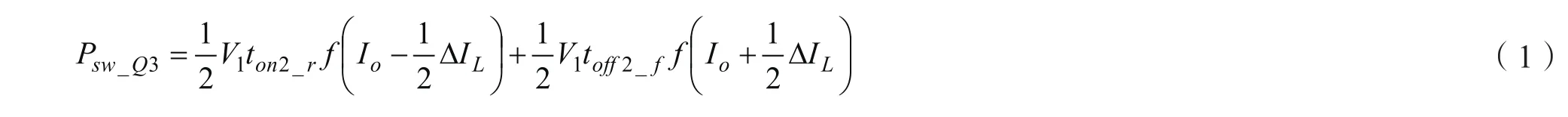
其中V1为Buck的输入电压,也是有源钳位正激谐振电路的输出电压,f为开关频率,LIΔ为电感纹波电流,ton2_r、toff2_f为Buck开关管Q3的导通上升时间和关断下降时间,Io是Buck的输出电流。可近似认为ton2_r=toff2_f=t。上式(1)可简化成:

(2)导通损耗
有源钳位正激谐振电路各开关管的导通损耗之和为:

式中)(1 rmsQI、)(2 rmsQI、)(5 rmsQI为一个周期内流过Q1、Q2、Q5的电流有效值,1QR、2QR、5QR为开关管Q1、Q2、Q5的导通电阻。

Buck电路各开关管的导通损耗之和为:

式中IQ3(rms)、IQ4(rms)为一个周期内流过Q3、Q4的电流有效值,RQ3、RQ4为开关管Q3、Q4的导通电阻。
根据Buck电路的工作原理,可得:

式中D2为Buck电路的占空比。Io是Buck的输出电流。
又因为选用的开关管Q3、Q4型号相同,所以RQ3=RQ4。

上式(5)可简化成:所以开关管的总导通损耗:
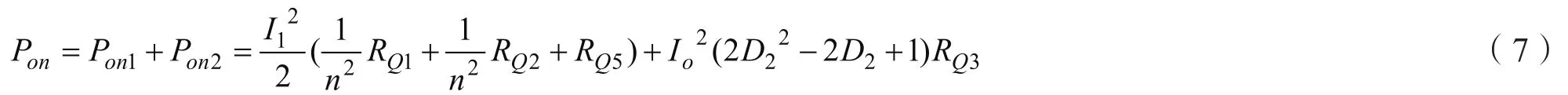
综上,两级式变换器的开关损耗和导通损耗之和为:

针对本实验参数t=100ns,f=300k,R=0.625ohm,

上式(8)可简化为:

上式(9)即为该两级式变换器的开关损耗和导通损耗之和与Buck电路的占空比D2、输出电流Io之间的数量关系。
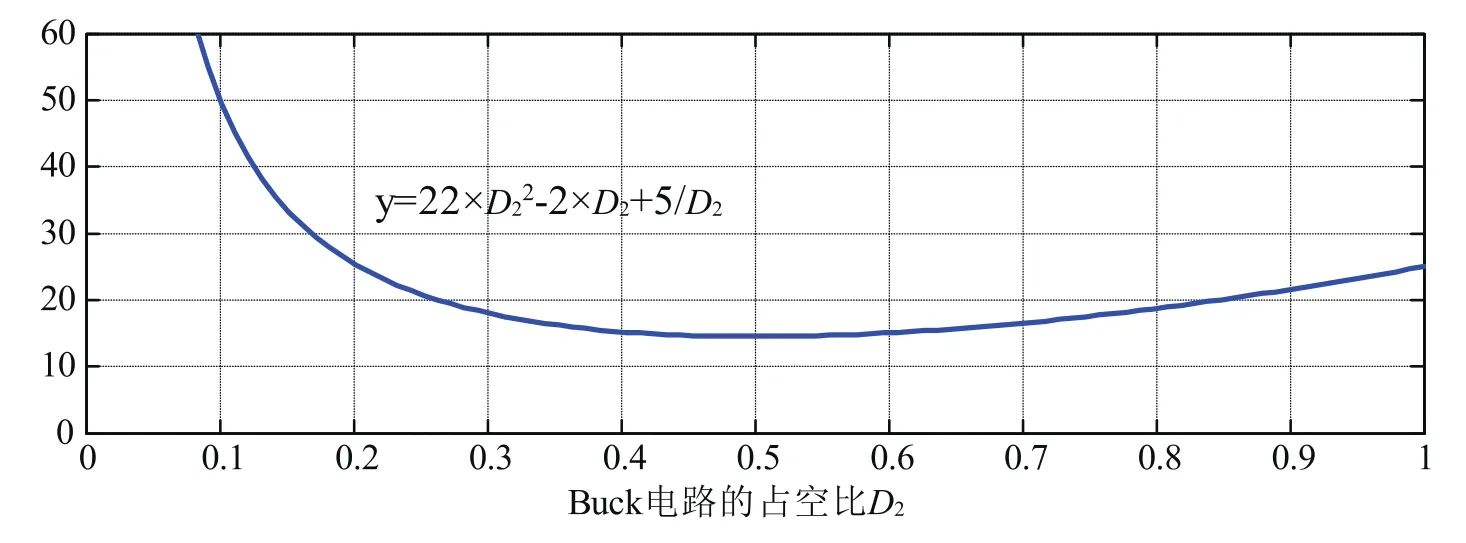
即当Buck的占空比为0.5时所对应的匝比是使得两级式变换器效率最高的。考虑到死区时间以及其他损耗的影响,Buck的占应比控制在0.4到0.45之间。
3 实验结果
采用“有源钳位正激谐振+Buck”方案,结合PCB表面贴元件技术,控制谐振电感Lr不变,通过改变变压器T原边匝比(副边匝比保持不变),从而改变Buck电路的占空比D2,搭建了输入48V,输出5V/8A的样机,电路的具体参数如表1所示:

表1 变换器参数Tab.1 Parameters of the converter
实验测得开关管Q2的栅源极电压波形2gV,谐振电流i的波形,第一级输出电压V1波形以及开关管Q3的栅源极电压波形3gV。测试了不同变压器T匝比下的实验波形,如下图(3)、(4)、(5)所示。最佳工作点的实验波形(图4)与理论分析计算的D2占空比波形相符。

为验证分析的正确性,分别测试了9:3;10:3;11:3;12:3;13:3;14:3;15:3这7种变压器匝比的(副边匝数保持不变,恒为3匝)两级式变换器的效率,并绘制了效率曲线,如图6所示。
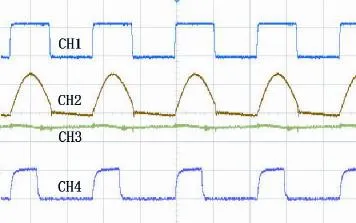
图3 匝比10∶3实验波形Fig.3 Waveforms of 10∶3
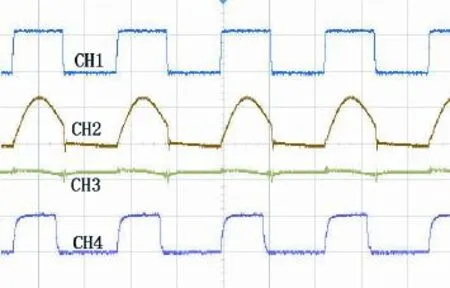
图4 匝比12∶3实验波形Fig.4 Waveforms of 12∶3
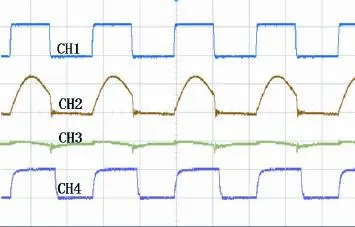
图5 匝比15∶3实验波形Fig.5 Waveforms of 15∶3
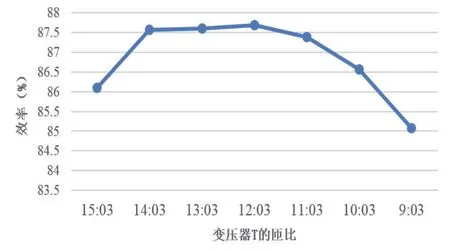
图6 测试的效率曲线Fig.6 Measured efficiency curves
从效率曲线图可以看出,当变压器T的匝比为12:3时两级式变换器的效率最高,接近88%,此时对应的Q3的占空比D2约为0.4,与理论分析相一致。
4 结论
本文详细分析了“有源钳位正激谐振+Buck”两级式变换器的开关损耗和导通损耗,量化了变压器的匝比与效率之间的关系。实验结果验证了计算所得变换器最优工作点的正确性。该变换器适用于48V母线电压输入的VRM,具有以下优点:①控制简单可靠,易于实现;②高效率;③工作稳定。
[1]Corporations I.Voltage Regulator Module(VRM)and Enterprise Voltage Regulator-Down(EVRD)11.1 Design Guidelines[J].2009.
[2]钱照明,何湘宁.电力电子技术及其应用的最新发展(一)[J].中国电机工程学报,1997,17(6):361-366.
QIAN Zhao-ming,HE Xiang-ning.Development of application of power electronics(Ⅰ)[J].Proceeding of the CSEE,1997,17(6):361-366.
[3]钱照明,何湘宁.电力电子技术及其应用的最新发展(二)[J].中国电机工程学报,1998,18(3):153-158.QIAN Zhao-ming,HE Xiang-ning.Development of application of power electronics(Ⅱ)[J].Proceeding of the CSEE,1998,18(3):153-158.
[4]LIANG X G,WEI J,RUAN X B.An interleaved-three level forward converter-suitable for the application of voltage regulator module[C].in Proc.IEEE PESC,Acapulco Mexico,2003:127-131.
[5]YE M,XU M,LEE F C.1MHz multi-resonant push-pull 48V VRM[C].in Proc.IEEE APEC,Miami Beach,Florida,USA,2003:413-419.
[6]梁小国,危建,阮新波.一种新颖的交错并联正激三电平变换器[J].中国电机工程学报,2004,24(11):139-143.LIANG Xiao-guo,WEI Jian,RUAN Xin-bo.A novel interleaved three-level forward converter[J].Proceedings of the CSEE,2004,24(11):139-143.
[7]WEI J,XU P,WU H P et al.Comparison of three topology candidates for 12V VRM[C].in Proc.IEEE APEC,Anaheim,California,USA,2001:245-251.
[8]YE M,XU P,YANG B,et al.Investigation of topology candidates for 48 V VRM[C].in Proc.IEEE APEC,Texas,USA,2002,(2):699-705.
[9]QIN W,ZHU B,ZHANG X,et al.A novel current-feed soft-switching two-switch forward resonant DC-DC Transformer(DCX)[C].2014 International Power Electronics and Application Conference and Exposition.IEEE,2014:126-130.
[10]刘晓东,韦燚.基于PID调节器的Buck电路的系统设计与仿真[J].新型工业化,2015,5(11):27-33.LIU Xiao-dong,WEI Yi.System design and simulation of Buck circuit based on PID regulator[J].2015,5(11):27-33.
[11]雷敏,孔令倩,邓昭俊.有源钳位交错并联反激拓扑微型逆变器仿真研究[J].新型工业化,2014,4(8):71-79.LEI Min,KONG Ling-qian,DENG Zhao-jun.Research on the active clamp interleaved flyback topology micro inverter simulation[J].2014,4(8):71-79.
[12]任小永,阮新波.适用于高压输入低压输出的两级式变换器[J].中国电机工程学报,2005,25(23):153-157.REN Xiao-yong,RUAN Xin-bo,Two-stage converter applicable to high voltage input low current output case[J].2015,25(23):153-157.
本文引用格式:WEI Xu-guang.The Interlayer Stress Analysis of Polyethylene-steel Composite Pipes[J].新型工业化,2016,6(7):28-33.
DOI:10.19335/j.cnki.2095-6649.2016.07.005
Abstract:Polyethylene-steel Composite Pipes is widely used in conveying corrosive media occasions,but the pipe may lose effectiveness in the process of transporting hot and cold media,so the research of stress distribution and variation in polyethylene-steel composite pipes is very necessary.This article frst assume that a thin adhesive layer is in between the polyethylene and steel,the adhesive layer along the axial shear stress is the major cause of the polyethylene layer and the steel pipe off sticky.Secondly,we use a method of fnite element to computer simulation by ANSYS,and verify initial assumptions.Finally,based on simulation data,we analyse the adhesive layer stress distribution and the variation with different parameters to change.Through the above research,preliminarily summarize the variation and distribution of interlaminar stress,and provide technical support for future design and process improvement of polyethylenesteel pipe.
Keywords:Laminated Polyethylene-steel Composite Pipes;Interlaminar Stress;Finite elements;ANSYS
Citation:WEI Xu-guang.The Interlayer Stress Analysis of Polyethylene-steel Composite Pipes[J].The Journal of New Industrialization,2016,6(7):28-33.
1 Introduction
Due to the outstanding corrosion-resistance character of the polyethylene-steel composite pipes(PSCP),it had been widely used into corrosive fluid transporting and different chemical industry fields.However,during past long term of practical applications it turns out that the constantly separation of polyethylene layer and steel layer causing pipe jam had limited the further application and became the main cause of all failure of polyethylene-steel composite pipes[1].There is a very thin glue layer between the polyethylene layer and the steel layer,which under circulate thermal working conditions we assume would be a powerful axle tangential stressed,which be considered as the main cause of the constantly separation of polyethylene layer and steel layer.Unfortunately,we don't pay attention to this phenomenon at home and abroad,but also the lack of relevant technical information,so the research of polyethylene-steel composite pipes interlaminar stress distribution and variation is very necessary.This paper first assumption that the polyethylene-steel composite pipes has a thin adhesive layer between the thermal expansion and contraction and the role of stress,the adhesive layer by a larger,along the axial shear stress is the major cause of the PE layer and the steel pipe off sticky.Secondly,we use a method of finite element[2]to computer simulation by ANSYS[3]and obtain the reference of some typical operating conditions simulated data for the future engineering applications,verified initially assumptions.Finally,based on simulation data,we analyse the adhesive layer stress distribution and the variation with different parameters to change.
2 Problem description and model
2.1Physical descripiton of problem
The structure of polyethylene-steel composite pipes[4]is shown in Figure 1.the outer layer is steel while the inner layer is polyethylene material solidified from hot air spraying,the relevant physical and
geometrical parameters is listed in Table 1.

Tab.1 The physical and geometrical parameters of PSCP
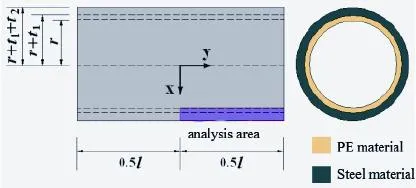
Fig 1.Thephysical model of polyethylene-steel composite pipe
2.2Mathematical description and model
Three directions of stress distribution should be taken into consideration during the analysis of stress components between polyethylene layers and steel layers such as:σx,σy,σzand τy,τxyz,τxz.The following formula was derived based on the relationship between the stress and variation of orthogonal isotropic material at the main direction:

According to plane coordinate conversion,it can be transferred into:

Where,σ1,σ2,σ3,σx,σy,σzrepresent axial stress;1,ε1,ε2,ε3,εx,εy,εzrepresent relevant axial stress strain;τ12,τ23,τ13,τxy,τyz,τxzrepresent tangential stress;γ12,γ23,γ13,γxy,γyz,γxzrepresent relevant tangential stress stain.
3 Experiment and data analysis
3.1Experimental scheme
In this paper,we make a thermal expansion model to model and postprocess and use common working condition that DN=60mm,L=3m as example:
1)Modeling with soild45 finite element
2)Inputting material data is shown in Table 1
3)The outcome of modeling procedure is shown in Figure 2 and Figure 3
Mostly,classic procedure of computer simulation progress are as follows:
1)With reference to the existing grid method[5-6],we impose symmetry constraints in caliber .Only a quarter of entire pipe is modeled to reduce workload of computer simulations and work intensitythe.The symmetrical and axial displacements is applied at two symmetrical section and center of pipe respectively according to current means of meshing and modeling.

Fig.2 Tangential stress distribution between layers
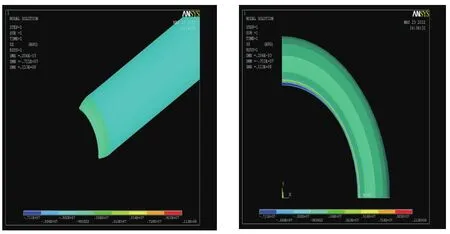
Fig.3 Axial stress distribution between layers
2)Inputting reference temperature:25°C,the working temperature of this single simulation is 30℃.
3)Computer calculating and data recording
3.2Raw data record and process
3.2.1Raw thermal expansion data of PSCP
The maximum axial stress and tangential stress calculated by the following relevant parameters:the reference temperature is 25°C and the working temperature are 30°C,35°C,40°C,45°C,50°C,55°C,60°C,65°C;the length of pipe are 2m,3m,4m,5m,6m,7m,8m,9m,10m respectively;the diameter of pipe are 20mm,40mm,60mm,80mm,100mm respectively.
Considering that there are three variables,in order to facilitate the calculation and display of results,we take DN as the group variable,the temperature and the length of pipe as within-group variation.Because of the limited paper space,only a list of maximum radial force and normal stress,of which the length L=1,2,3...10mm and DN=20,40 mm .The details are as follows:

Tab.2 Raw data of the maximum tangential stress at DN=20mm

Tab.3 Raw data of the maximum axial stress at DN=20mm

Tab.4 Raw data of the maximum tangential stress at DN=40mm

Tab.5 Raw data of the maximum axial stress at DN=40mm
3.2.2Raw intial stress raw data of manufacturing PSCP
The simulation working condition in this section is that pipe diameter:DN=80mm,pipe length:L=2m,manuf- acturing temperature:300°C[7],cooling temperature:20°C,the outcome data is as follows(which is dominated by practical computer performance used in this paper that no longer lengthscould be simulated otherwise the program would report error and exit):
As shown in Figure 4 and Figure 5,from simulation results,we can find that the maximum stress concentrate on the surface of steel layer and the tangential stress is greater than the axial stress along the simulations.

Tab.6 Raw data of the initial maximum tangential stress at DN=80mm

Tab.7 Raw data of the initial maximum axial stress at DN=100mm
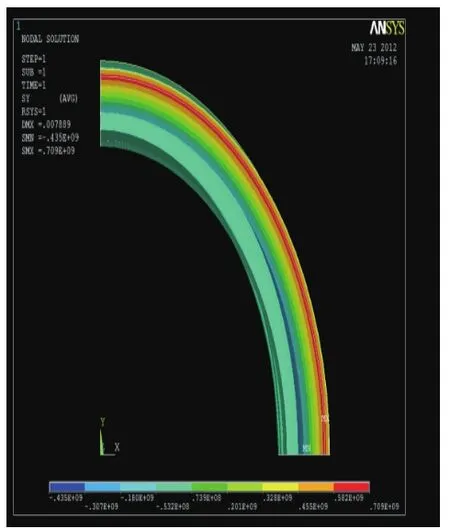
Fig.4 The distribution of maximum initial tangential stress

Fig.5 The distribution of maximum initial axial stress
3.3Data analysis
3.3.1Regular pattern of Srz & Sr changing with pipe Length
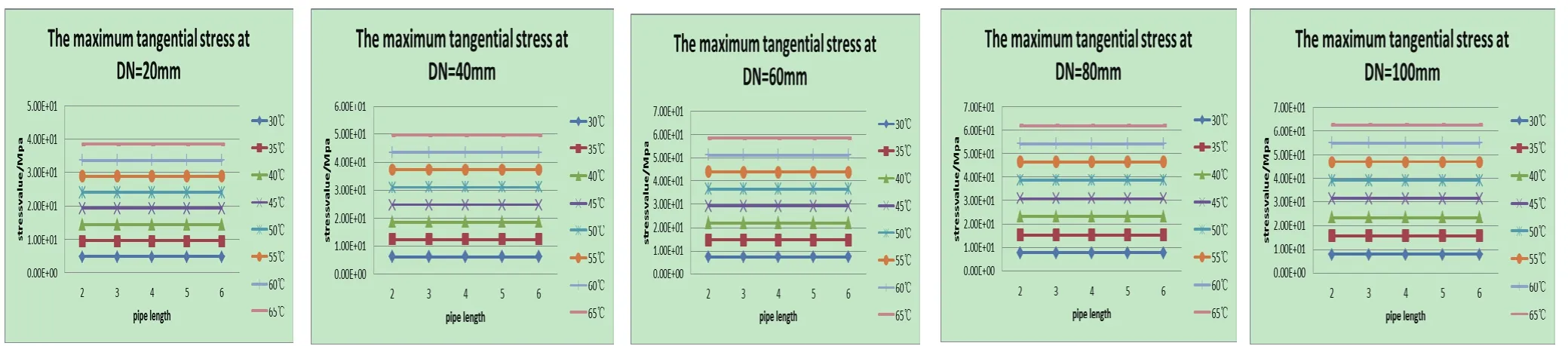
Fig.6 The maximum tangential stress with the change of diameter

Fig.7 The maximum axial stress with the change of diameter
3.3.2 Regular pattern of Srz & Sr changing with pipe diameter
3.3.3Regular pattern of Srz & Sr changing with working temperature
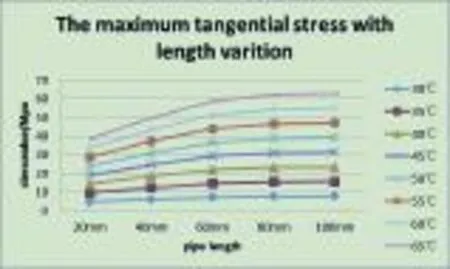
Fig.8 The maximum tangential stress with the change of length

Fig.9 The maximum axial stress with the change of length
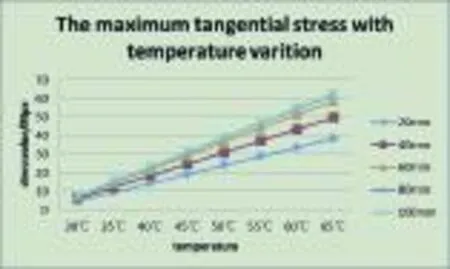
Fig.10 The maximum tangential stress with the change of temperature
3.3.4Stress distributions along the diameter of PSCP pipe
Common simulation parameters:DN=80mm,L=6m,reference temperature T1=25°C,reference temperature T2=60℃
3.3.5Initial Stress distributions along with the diameter of PSCP pipe
3.4Major conclutions
1)The interlayer stress variation regularity with the pipe
length:As shown in Fig 6 and Fig 7,both tangential and axial stress distribution is only related to temperature variation,which is not related to diameter variation according to mass mount of data analyses.
2)Regular pattern of interlayer stress along with diameter variation according to Fig 8 and Fig 9:
(1)Both the tangential and axial stress increase with the increasing of pipe diameter.
(2)Both the absolute value of the maximum tangential and axial stress decrease with the increasing of pipe diameter.
(3)The maximum tangential stress Srz increase with the increasing of the absolute value of pipe diameter.
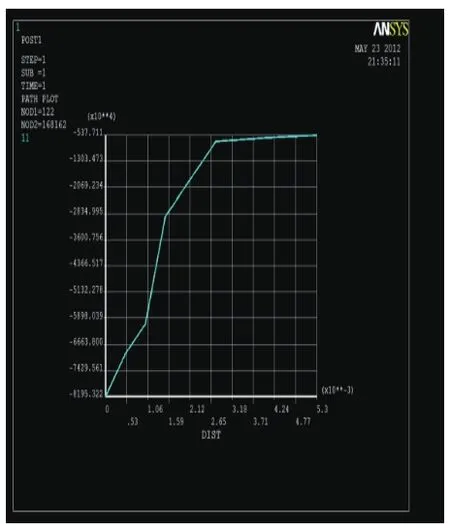
Fig.12 The maximum tangential stress distribution along with pipe diameter
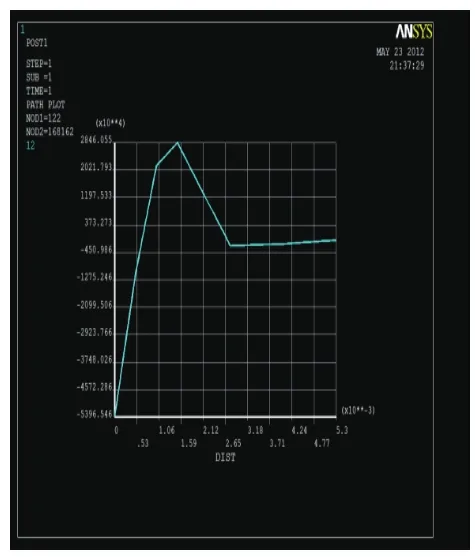
Fig.13 The maximum axial stress distribution alongwith pipe diameter
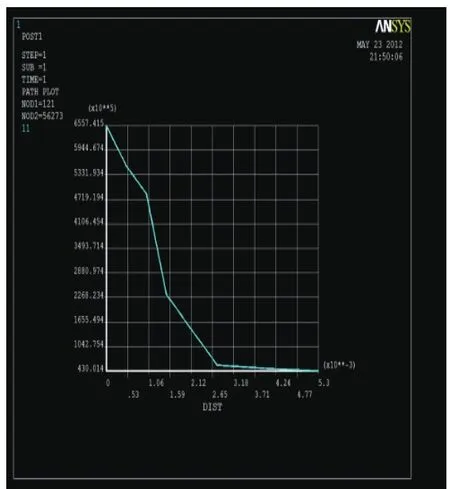
Fig.14 The initial tangential stress distributionalong pipe diameter

Fig.15 The initial axial stress distribution alongpipe diameter
3)Both the tangential and axial stress is linear relative to the temperature variation according to Fig 10,Fig 11within the given temperature region(30℃-65℃).
4)The relationship between the maximum tangential stress and axial stress:the maximum axial stress usually is greater than the maximum tangential stress which is usually within the difference belowan order of magnitude when the temperature difference is little,however,the difference between them increase with the increase of temperature difference,especially when the temperature difference is very big,the maximum axial stress is far greater than the relevant tangential stress.
5)The tangential stress distribution along with the classic common used diameter of pipe:the tangential stress decrease with the pipe diameter.
6)The axial stress distribution along with the classic common used diameter of pipe:the maximum axial stress appeared at the contact layer of Polyethylene layer and steel layer according to Fig 13.
7)The distribution of initial stress under classic working condition:Manufacturing temperature:300℃,cooling temperature:20℃
(1)Distribution of initial tangential stress:the initial stress increase with the diameter from inner layer with the maximum value of 709Mpa.
(2)Distribution of initial axial stress:the maximum initial stress value of 472Mpa appeared at the contact layer between polyethylene layer and steel layer.
4 Summary and Outlook
This paper simulated stress distribution between those two layers via computer simulation under different groups of classic boundary conditions,trying to point out some regular pattern of polyethylene layer and steel layer with boundary condition changing.As the result of above research,we astonished find out that the stress between layers had not be taken into consideration by current pipe manufacturing technology,which would rise with the temperature difference rising and would became extremely dangerous to polyethylene-steel composite pipes when the temperature different gets very much from the original boundary conditions.We believe this paper testified the hypothesis proposed before and would provide some helpful reference value to the further improvement of polyethylene-steel composite pipes designing and manufacturing technology.But the conclusions of this paper based only on computer simulation than practical thermal-stress circulation experiment data,for which these conclusions can only be taken as technological references than actual experiment conclusions.In addition,The PE plastic layer was considered as static layer with static parameters such as elastic modulus,Poisson ratio and thermal coefficient of expansion,however,as everyone knows that the solidification of plastic material is dynamic and very complicated whose material parameters could not possibly be static and the same as normality,so the conclusions about initial stress distribution is only ideally simulated rather than the practical application situation.The actual distribution of initial stress need further study.
References
[1]Li Mingyang,Mechanical study on failure mechanism of buried PE gas pipeline[D].South China University of Technology,2010.
[2]Chen Xidong,Yang jie,Zhao Xiaodong,Fan Xiqiu,Finite element method develo pment status and application[J].Manufacturing information engineering of China,2010,11:6-8+12.
[3]Zheng Xiaoya,You Junfeng,Zhang Duo,Xu Chao.Application of ADAMS and ANSYS in the mechanism analysis[J].solid rocket technology,2010,02:201-204.
[4]Yang Weifang,Gu Sumin,Xu Zhiru.Low temperature resistance performance test of PE steel plastic composite pipe lining[J].Welded pipe,2011,07:27-30.
[5]E.Baranger a,O.Allix a,L.Blanchard b.A computational strategy for the analysis of damage in composite pipes.[J].Composites Science and Technology 69(2009)88-92.
[6]Hamidreza YazdaniSarvestani,Mohammadreza YazdaniS-arvestani nterlaminar stress analysis of general composite laminates.[J].International Journal of Mechanical Sciences 53(2011)958-967.
[7] Liu Huiyi.Process characteristics and The coating properties of steel tube hot coating EP and hot coating PE[J].welded pipe,2004,27(1).
An Optimal Operating Point Analysis of Two-stage Converter
HU Xiao-xiao,WU Kun
(College of Electrical and Information Engineering,Tongji University,Shanghai 201804,China)
This paper analyses the optimal design of a two-stage converter in detail,aims at resonant converter cascading Buck circuit,bases on the switching loss and conduction loss,quantifes the relationship between the transformer turns ratio and the effciency,and calculates the optimal operating point of the converter.The two-stage converter is suitable for 48V input bus voltage VRM,and solves the problems such as uncontrolled duty ratio and low effciency often come up against in traditional single converter.In addition,a prototype with 48V input and 5V/8A output is built to verify the analysis.
Two-stage converter;Optimal operating point;Switching loss;Conduction loss
The Interlayer Stress Analysis of Polyethylene-steel Composite Pipes
WEI Xu-guang
(Northeastern University Engineering & Research Institute Co.,Ltd,GuiYang 550000)
10.19335/j.cnki.2095-6649.2016.07.004
HU Xiao-xiao,WU Kun.An Optimal Operating Point Analysis of Two-stage Converter[J].The Journal of New Industrialization,2016,6(7):22-27.
胡潇潇(1991-),女,硕士研究生,主要研究方向为两级式变换器的效率优化;吴琨(1992-),男,硕士研究生,主要研究方向为变换器拓扑和控制策略。
