膜片弹簧离合器分离特性的分析计算与仿真

刘欣，张凯，丁殿磊，刘元杰

(大连理工大学机械工程学院，辽宁大连 116024)



膜片弹簧离合器分离特性的分析计算与仿真

刘欣，张凯，丁殿磊，刘元杰

(大连理工大学机械工程学院，辽宁大连 116024)

简要介绍了电控机械式自动变速器(AMT)中膜片弹簧离合器的性能特点。在此基础上，根据已有的膜片弹簧计算公式对膜片弹簧从自由状态到接合状态再到分离状态进行了深入的分析与计算，得出了压力与形变的函数关系。通过MATLAB软件对推导出的4组函数关系进行仿真，从仿真曲线可以清晰地看出压力与变形的线性关系，从而可以实现离合器的分离控制。

离合器；膜片弹簧；分离特性；MATLAB仿真

0　引言

电控机械式自动变速器具有传动效率高且成本低的优点，因此成为近些年来研究的热点之一[1]，但它的难点在于离合器的分离与接合的控制，而近年来以膜片弹簧离合器应用最为广泛。所以，膜片弹簧的大小端压力与位移函数关系将对离合器的分离与接合的控制起到至关重要的作用。

1　膜片弹簧离合器

在当前汽车领域中，已广泛采用膜片弹簧离合器。膜片弹簧离合器的结构特点如下：

(1)膜片弹簧的轴向尺寸较小而径向尺寸很大，有利于在提高离合器传递扭矩的情况下减小离合器的轴向尺寸；

(2)膜片弹簧的分离指起到分离杠杆的作用，故不需要专门的分离杠杆，使离合器的结构大大简化，零件数目少且质量轻；

(3)由于膜片弹簧轴向尺寸小，所以可以适当增加压盘的厚度，还可以在压盘上增加散热筋及在离合器盖上开设较大的通风孔来改善散热条件[2]。

2　膜片弹簧的分离特性分析与计算

根据分离时分离指内端受推力还是拉力，膜片弹簧离合器可分为推式膜片弹簧离合器和拉式膜片弹簧离合器。但无论推式还是拉式，其基本原理都是相同的。所以分析计算过程中可采用相同的力学分析模型。

但在做力学分析过程中，有必要对膜片弹簧做出相应的假设：

(1)膜片弹簧小端所受的压力必须均匀地分布在膜片弹簧的四周，如此一来，膜片弹簧在轴向产生的变形才会均匀；

(2)膜片弹簧从压紧到分离及返回的过程中，摩擦力忽略不计；

(3)膜片弹簧虽然不像一般的螺旋弹簧，但在该过程中也不产生塑性变形。

2.1大端压力与大小端变形的关系

膜片弹簧受载荷变形如图1所示。

图中：r为小端半径；R为大端半径；H为膜片弹簧的内截面高；h为钢板厚；E为弹性模量，取E=2.05×105MPa；μ为泊松比，取μ=0.3；k为形变。

在图1中，载荷P与形变k的关系为[3]：

(1)

设自由状态到承载状态的圆锥角度从w变化到v，变化量为θ。则对于θ的求解有以下两种方法：

(1)近似代替法。w与v的大小分别为：

(2)

式中：r′为承载状态时的小端半径。

由于膜片弹簧本身的圆锥角度很小，所以：

(3)

所以变化的角度：

(4)

由于小端半径变化非常小，所以认为：

r=r′

(5)

(2)省略法。因为θ等于w减去v，所以

(6)

但由于：

(7)

所以：

(8)

在图2中，膜片弹簧从自由状态到接合状态的过程与图1相同，若两图中膜片弹簧转过相同的角度θ时，可得：

(9)

则由式(9)可得：

(10)

由于转过的角度相同，则图1中载荷P和图2中载荷P1所产生的转矩相等，即：

P(R-r)=P1(L-l)

(11)

所以得：

(12)

将式(10)与式(12)代入式(1)得大端压力与大端变形的关系为：

(13)

当在小端施加压力P2后，产生小端变形k2，由：

(14)

得：

(15)

在接合状态时，总压力为P，由于此时P2=0，所以P1=P，又因为P所产生的转矩是恒定不变的，所以随着P2的增大，P1在减小，即:

P(L-l)=P1(L-l)+P2(l-rf)

(16)

k1为大端变形，而令k1max为大端的最大变形，则：

k1max=k11+k21

(17)

式中：k11为P在大端产生的变形；k21为P2在大端产生的变形。

而式(13)是在未施加P2，即大端变形为k11的情况下得出的，又因为P1在大端产生的变形很小，可忽略P1在大端产生的变形，即k22=k2，所以：

(18)

那么将式(18)代入式(13)可以得出大端压力与小端变形之间的关系：

(19)

2.2小端压力与大小端变形的关系

因为P的值等于未施加P2时的P1值，所以当膜片弹簧处于分离状态时，P1=0，此时式(16)即为：

P1(L-l)=P2(L-rf)

(20)

可得：

(21)

将式(21)代入式(13)得小端压力与大端位移的关系为：

(22)

将式(21)和式(15)代入式(13)得小端压力与小端位移之间的关系为：

(23)

3　基于MATLAB的仿真计算

k1max的值可由式(13)两次求导得k1max=5.79 mm。

表1中的参数值是8～10 m公交客车上常用的膜片弹簧的参数值。根据以上数据和推导公式可以用MATLAB软件仿真得出P1与k1、P2与k1、P1与k2以及P2与k2的关系曲线。

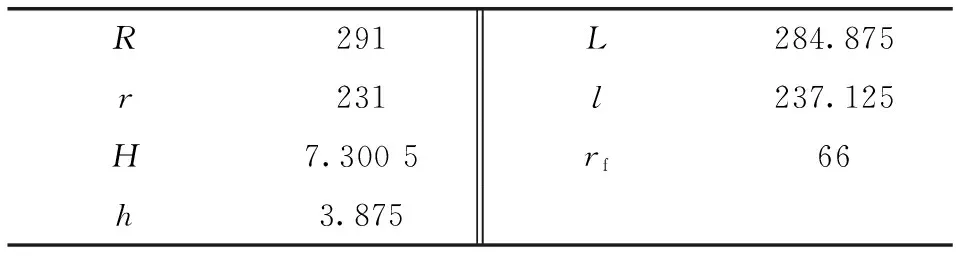
表1　膜片弹簧的基本参数　mm

从图3中可以看出：当膜片弹簧的小端位移大约在16 mm时，大端压力已变为0，离合器就进入了分离状态，接下来就可以进行换挡操作了。

4　结束语

从理论上对膜片弹簧的4组关系进行了推导，虽然通过仿真得出了当小端位移为16 mm时，离合器就进入了分离状态。但在实际使用过程中，许多现实因素又会对离合器的分离控制产生一定的影响。正如前文中所讲，在膜片弹簧工作过程中忽略了摩擦因素，但在现实中这是不可避免的。所以，文中研究仅对实现离合器的最佳分离控制提供了相应的理论基础。

【1】郑磊.解放载货车机械式自动变速器控制技术研究[D].长春：吉林大学,2004.

【2】陈家瑞.汽车构造[M].北京:机械工业出版社,2013.

【3】刘惟信.汽车设计[M].北京:清华大学出版社,2005.

Analysis Calculation and Simulation for Disengagement Characteristic of Diaphragm Spring Clutch

LIU Xin,ZHANG Kai,DING Dianlei,LIU Yuanjie

(School of Mechanical Engineering, Dalian University of Technology, Dalian Liaoning 116024, China)

The performance characteristics of diaphragm spring clutch in automatic mechanical transmission were described. Then according to the calculation formula of diaphragm spring, analyses and calculation about from the free state to the junction state and then to separated state were made. The function relationship between pressure and deflection was gotten. Through MATLAB software, 4 sets of derived functional relations were simulated.From the simulation curves, a linear relationship between pressure and deflection was obtained. Thus separation control of the clutch can be achieved.

Clutch; Diaphragm spring; Disengagement characteristic; MATLAB simulation

2016-04-30

刘欣(1956—)，男，博士，副教授，主要研究领域为汽车电子技术、汽车轻便换挡理论及应用、汽车自动变速理论及应用、智能仪器仪表的研究及应用。E-mail：liushi28958@163.com。

张凯，E-mail：1023312360@qq.com。

U463.211

A

1674-1986(2016)07-007-04