怎样解方程应用题
2016-08-26于宗英彭景才
文/于宗英 彭景才
怎样解方程应用题
文/于宗英彭景才

方程应用题是中考的重要内容,这类问题类型众多,背景鲜活,具有很强的时代感.下面以2015年中考题为例,对应用题进行归类解析,希望对你的复习有所帮助.
一、增长率问题
例1(2015年长沙卷)现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求快递总件数的月平均增长率;
(2)如果平均每人每月最多可投递快递0.6万件,那么该公司现有21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
解析:(1)设快递总件数的月平均增长率为x,由已知得10(1+x)2=12.1,
解得x1=0.1,x2=-2.1(舍去).
答:该公司快递总件数的月平均增长率为10%.
(2)今年6月份快递投递任务有12.1×1.1=13.31(万件).
21×0.6=12.6<13.31,
∴21名快递投递业务员不能完成今年6月份的快递投递任务.
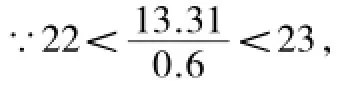
∴至少还需增加2名业务员.
温馨小提示:若基础量为a,连续增长(或降低)n次,最后的结果量为b,设平均增长(或降低)率为x,则增长后的方程为a(1+x)n=b或降低后的方程为a(1-x)n=b,求出方程的解后,要注意根据实际问题检验结果的合理性.
二、水费问题
例2(2015年深圳卷)下表为深圳市居民每月用水收费标准(单位:元/m3):
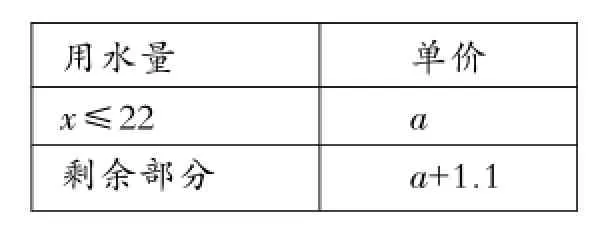
用水量 单价_ x ≤2 2 a剩余部分 a + 1 . 1
(1)某用户用水10立方米,交水费23元,求a的值;
(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?
解析:(1)由题意可得10a=23,解得a=2.3.
(2)设用户用水量为x立方米,
∵用水22立方米时,水费为22×2.3=50.6<71,
∴x>22,
∴22×2.3+(x-22)×(2.3+1.1)=71,解得x=28.
答:该用户用水28立方米.
温馨小提示:根据图表中数据估算出用户用水量x米3(x>22)是解题的关键.
三、图表信息问题

图1
例3(2015年吉林卷)根据图1中的信息,求梅花鹿和长颈鹿现在的高度.
解析:设梅花鹿的高度是xm,长颈鹿的高度是ym.
答:梅花鹿的高度是1.5m,长颈鹿的高度是5.5m.
四、车费问题
例4(2015年娄底卷)假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底火车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
解析:(1)设出租车的起步价是x元,超过1.5千米后每千米收费y元.
答:出租车的起步价是4.5元,超过1.5千米后每千米收费2元.
(2)5.5千米的路程分两段收费,根据(1)中的单价可得
4.5+(5.5-1.5)×2=12.5(元).
答:小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费12.5元.
温馨小提示:利用二元一次方程组解应用题需要找到2个等量关系,找到恰当的等量关系并用方程表示出来是解题的关键.
五、行程问题
例5(2015年烟台卷)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程约为1026千米,高铁平均时速为普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到当日8:40从烟台至某市的高铁票,而且从该市火车站到会议地点最多需要1.5小时,试问在高铁列车准点到达的情况下他能在开会之前到达吗?
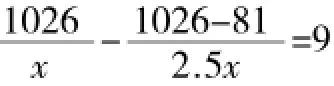
经检验,x=72是原分式方程的解,且符合题意,则2.5x=180,
答:高铁列车的平均时速为180千米/时.
(2)630÷180=3.5,则坐车共需要3.5+1.5=5(小时),
王老师到达会议地点的时间为13点40分.
故他能在开会之前到达.
温馨小提示:行程问题中的基本关系式是:路程=速度×时间,根据三者的关系,找到相等关系,列出方程.在列方程时注意统一单位.
六、面积问题
例6(2015年湖北卷)如图2,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
解析:设矩形猪舍垂直于住房墙一边长为xm,则平行于墙的一边的长为(25-2x+1)m,由题意得
x(25-2x+1)=80,
化简,得x2-13x+40=0,
解得x1=5,x2=8,
当x=5时,26-2x=16>12(舍去),
当x=8时,26-2x=10<12,符合题意.
答:所围矩形猪舍的长为10m、宽为8m.
温馨小提示:利用面积公式,将实际问题转化为数学问题,构造方程模型来解决,要注意题目中的限制条件.
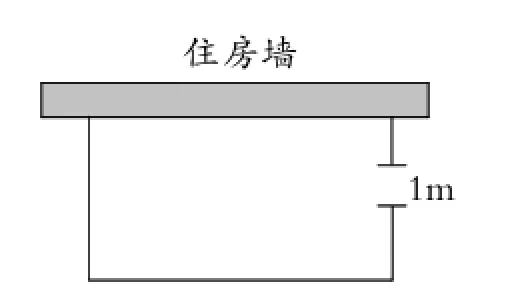
图2
七、方案问题
例7(2015年桂林卷)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各是多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
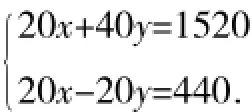
答:每本文学名著和动漫书的价格分别为40元和18元. (2)设学校购买文学名著m本,动漫书为(m+20)本,则有

因为m为整数,所以m取26,27,28.
方案一:文学名著26本,动漫书46本;方案二:文学名著27本,动漫书47本;方案三:文学名著28本,动漫书48本.
温馨小提示:二元一次方程组与不等式组是解决方案问题的常见工具,需要弄清题意,找出题目中的等量关系与不等关系,列出方程与不等式.
