Nuclear field shift effects on stable isotope fractionation：a review

Sha Yang·Yun Liu



Nuclear field shift effects on stable isotope fractionation：a review

Sha Yang1，2·Yun Liu1

©The Author（s）2016.This article is published with open access at Springerlink.com

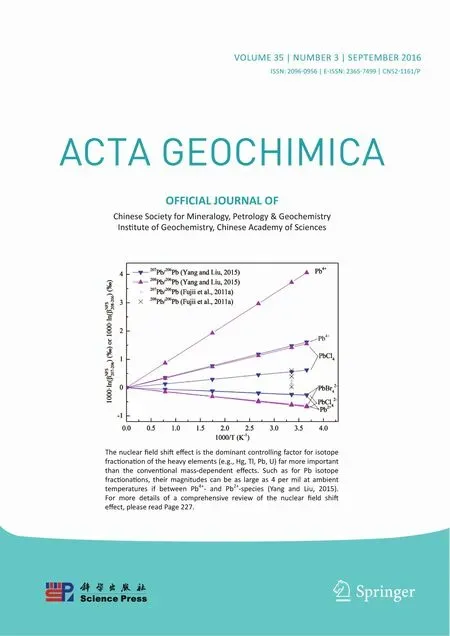
An anomalous isotope effect exists in many heavy element isotope systems（e.g.，Sr，Gd，Zn，U）.This effect used to be called the‘‘odd-even isotope effect'' because the odd mass number isotopes behave differently from the even mass number isotopes.This mass-independent isotope fractionation driving force，which originates from the difference in the ground-state electronic energies caused by differences in nuclear size and shape，is currently denoted as the nuclear field shift effect（NFSE）.It is found that the NFSE can drive isotope fractionation of some heavy elements（e.g.，Hg，Tl，U）to an astonishing degree，far more than the magnitude caused by the conventional mass-dependent effect（MDE）.For light elements，the MDE is the dominant factor in isotope fractionation，while the NFSE is neglectable.Furthermore，the MDE and the NFSE both decrease as temperatures increase，though at different rates.The MDE decreases rapidly with a factor of 1/T2，while the NFSE decreases slowly with a factor of 1/T.As a result，even at high temperatures，the NFSE is still significant for many heavy element isotope systems.In this review paper，we begin with an introduction of the basic concept of the NSFE，including its history and recent progress，and follow with the potential implications of the inclusion of the NFSE into the kinetic isotope fractionation effect（KIE）and heavy isotope geochronology.

Isotope fractionation·Mass-dependent effect· Nuclear field shift effect·Mass-independent fractionation· Nuclear volume effect·Nuclear shape effect

1 Introduction

From a spectroscopic view，isotope shifts include the mass shift and the field shift（King 1984）.The mass shift is induced by the difference between isotope masses which is also called mass-dependent effect.The conventional equilibrium stable isotope fractionation theory for the mass shift was established by Bigeleisen and Mayer（1947）and by Urey（1947）.This theory predicts that the isotope enrichment factor is proportional to the isotopic mass difference，Δm，and inversely proportional to the product of masses m and m′of the two isotopes，when the temperature is constant.The field shift is a short expression of the nuclear field shift effect（NFSE），an anomalous isotope effect（i.e.，mass-independent fractionation）caused by the difference in the nuclear size and shape of isotopes.It is also called the nuclear volume effect（NVE）because the nuclear shape effect is very small and the nuclear volume effect dominates.The nuclear field shift effect predominantly affects the isotope fractionation of heavy elements，but not light elements.

The anomalous isotope effect was first reported for metals by Fujii et al.（1989a，b）in the U（IV）-U（VI）exchange reaction.It is found that the isotope fractionation of the odd mass number isotope235U deviates from the mass-dependent lines defined by even mass number isotopes.The isotope fractionations of157Gd and67Zn are similar to235U which belong to mass-independent in liquid-liquid extraction experiments（Chen et al.1992；Nishizawaetal.1993）.Thisanomalousisotopefractionation phenomenon used to be called the‘‘odd-even isotope effect''（Nishizawa et al.1994）（Fig.1）but its mechanism was not clear.

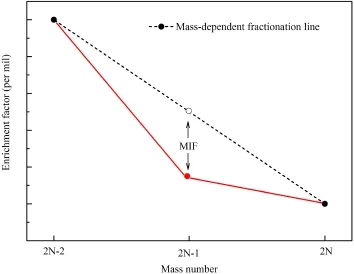
Fig.1 Variation of the enrichment factor with isotopes.N is a positive integer.The red line is the real fractionation line.The red solid circle（the odd number isotope）deviates from the massdependent line composed of even mass number isotopes

Nishizawa et al.（1995）interpreted the similar anomalous isotope effect of87Sr as being caused by the field shift in the liquid-liquid extraction of strontium chloride，using a crown ether.This is the first paper that clarified the cause of this kind of anomalous isotope effect.Nomura et al. （1996）found that233U shows anomalous mass-independent fractionations in the U（IV）-U（VI）exchange reaction，similar to those results in previous paper（Fujii et al. 1989a，b），and suggested that the cause was the field shift.

After a private communication with the Yasuhiko Fujii's group，Bigeleisen（1996）theoretically revised the reduced partition function ratios of uranium ions in solution.In his revision，the terms of the hyperfine splitting and the nuclear field shift effect（NFSE）were added to his theoretical treatment of isotope fractionation.He noticed that the hyperfine splitting was an order of magnitude smaller，explaining the anomaly in the238U/235U separation in the U（III）-U（VI）exchange reaction.His results of the nuclear field shift effect are three times as large as the conventional mass-dependent fractionation，and show that heavier isotopes preferred to be enriched in U（IV）in the U（IV）-U（VI）exchange reactions.Since then，the NFSE has become an important correction term to the conventional Bigeleisen-Mayer equation for heavy elements.In a following paper，Bigeleisen also noticed that the NFSE was just a second order correction in chemical bonds（Bigeleisen 1998），indicating that the NFSE has a minor effect on vibrational frequencies（i.e.，on the conventional mass-dependent isotope fractionation）.Importantly，the paper first pointed out that the NFSE could induce large isotopic fractionations through the variation of ground-state electronic energy alone.

Fig.2 a Root mean-square（RMS）nuclear charge radii（＜r2＞1/2）of U isotopes（Fricke and Heilig 2004）.The odd atomic mass number isotope （235U）is smaller than the trend line through the even atomic mass number isotopes（234U and236U）.b Plots of δ＜r2＞vs.Δm/mm′for U isotopes，showing not a straight line

The nuclear field shift effect scales with the difference in the mean-square nuclear charge radius of different isotopic nuclei（i.e.，NFSE∝δ＜r2＞and δ＜r2＞= ＜r2＞A-＜r2＞A′，where A and A′represent heavy and light isotopes，respectively）（King 1984）.A well-known phenomenonisthatthemean-squarenuclearradii （i.e.，＜r2＞）do not follow a simple straight line with the number of neutrons increasing.Odd atomic mass number isotopes of many heavy elements（e.g.，235U）tend to be smaller than the trend line through the adjacent isotopes with even atomic mass numbers（e.g.，234U and236U）of the same element.This is called odd-even staggering in the atomicspectra（King1984）（Fig.2a）.Theabove-mentioned odd-even isotope effect is similar to the oddeven staggering.Moreover，δ＜r2＞varies with Δm/mm′nonlinearly，which shows that the nuclear field shift effect induces mass-independent isotope fractionation（Fig.2b）.

The experiments also find the heavier isotopes of U to be preferentially enriched in U（IV）rather than U（VI）in redox reactions（Fujii et al.1989a；Nomura et al.1996，Wang et al.2015）.However，the conventional isotope fractionation theory estimates that the heavier isotopes（54Cr，56Fe，238U，etc.）would be enriched in the higher oxidized states instead of the lower oxidized states.Assumedly，such mismatch is caused by the NFSE，but with no further evidence.This could be an important research topic for the near future.

2 Conventional mass-dependent fractionation

2.1Isotope fractionation factor α

Consider an isotope exchange reaction

where A and A′are the heavy and light isotopes of the element A；X and Y are different compounds.The isotope fractionation factor for this reaction is defined as α= （A/A′）AY/（A/A′）AX，an isotope concentration ratio between AX and AY.The isotope enrichment factor is defined as ε=α-1≈lnα.

2.2Bigeleisen-Mayer theory or Urey model

Bigeleisen and Mayer（1947）and Urey（1947）proposed a well-known equation for calculating the isotope fractionation extent of an isotope exchange reaction，called the Bigeleisen-Mayer equation（hereafter the B-M equation）or the Urey model.This equation，actually based on the Born-Oppenheimer approximation，assumes several harmonic approximations as well.According to the B-M equation，the logarithm of the isotope fractionation factor for the exchange reaction（1）is

where（s/s′）f is the reduced partition function ratio（RPFR）. Under high-temperature approximations，the（s/s′）f of AX/A′X is

where m and m′are the masses of the heavy and light isotopes，respectively；Δm is the relative mass difference of isotopes（i.e.，Δm=m-m′）；mxis the mass of the compound X；and nxis the number of compound X.In Eq.（3），uXis defined as

where h and k are Planck and Boltzmann constants；c is light velocity；T is the absolute temperature and ωXis the wave number of the harmonic oscillation of the stretching motion.The expression of（s/s′）f（AY/A′Y）is similar to（s/s′）f（AX/A′X）.Sotheexpressionoftheisotope enrichment factor is

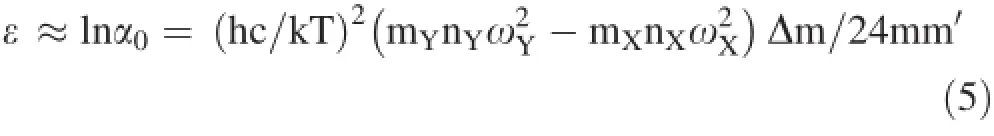
From Eq.（5），the enrichment factor is proportional to Δm/（mm′T2）.When the temperature is constant，the enrichment factor is proportional to Δm/mm′.Therefore，theisotopefractionationfactordecreaseswiththe increasing atomic number.According to the B-M equation，the isotope fractionation of heavy elements would be extremely small even at low temperatures.

The mass-dependent fractionation（MDF），as described by the B-M equation，only considers the difference in kineticenergies（i.e.，rotationalenergy，translational energy，and vibrational energy）of the two isotopologues，neglecting the difference in their electronic energies.This approximation treatment is，however，improper for heavy elements.The MDF contribution is only one part of the total isotope fractionation.

2.3Revised isotope fractionation theory

For a uranium isotope exchange reaction，Fujii and coworkers（1989a）found the ratio of theoretically predicted isotope enrichment factors between234U/235U and235U/238U is 1/3.This is distinctly different from the experimental value of 1/7.In addition，they observed a clear deviation from the mass-dependent isotope fractionation line theoretically predicted by the B-M equation for 235U.

Bigeleisen（1996）extended the isotope fractionation factor containing the nuclear spin and the nuclear field shift effect as well as the mass-dependent effect.The logarithm of the revised isotope fractionation factor becomes（Bigeleisen 1996）

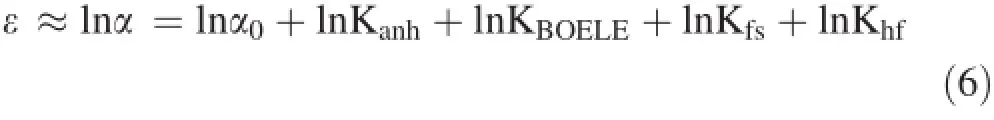
where lnα0is the isotope fractionation factor under the B-M equation approximations；lnKanhis the anharmonic correction term；lnKBOELEis the correction to the Born-Oppenheimer approximation；lnKfsis the contribution from the nuclear field shift effect；and lnKhfis the term for nuclear spin effect.Because of extremely small contributions of the anharmonic correction for heavy elements，the lnKanhcan be neglected（Bigeleisen 1996）in calculatingthe enrichment factor for heavy elements.The correction to Born-Oppenheimer approximation is related to masses of isotopes and is proportional to Δm/mm′（Kleinman and Wolfsberg 1973，1974）.Therefore，lnα0and lnKBOELEare both proportional to Δm/mm′when the temperature is constant.Nuclear spin effect exists only when the isotopic mass number is odd.Bigeleisen（1996）indicates that the nuclear spin effect is too small to account for the anomalous isotope effect of238U/235U separation in the U（III）and U（VI）exchange reaction and can be safely neglected in the investigation of U isotope exchange reactions.

Under the approximations used in the B-M equation，a nucleus is considered as a point charge.However，the isotopes of heavy elements have the same number of protons but different number of neutrons.This can cause the difference in nuclear size and shape（e.g.，235U vs.238U）（Fig.3）.Therefore，their ground-state electronic energies will also be different（Table 1）.The difference in electronic energies can no longer be neglected for the isotopes of heavy elements.This is completely ignored in the conventional B-M equation.

Fig.3 Nuclei of the isotopes of heavy elements with finite nuclear sizes.The different numbers of neutrons cause the difference in nuclear size and shape of isotopes（i.e.，difference in nuclear radius r1and r2）.For example，the root mean-square nuclear charge radius＜r2＞1/2of235U and238U are 5.834 fm and 5.860 fm（Fricke and Heilig 2004），respectively

3 Nuclear field shift effect

In the 20th century，several researchers（e.g.，Stacey 1966；Heilig and Steudel 1978；King 1984；Aufmuth et al.1987）proposed the concept of the‘‘nuclear field shift effect''in the atomic spectra but failed to apply it to the study of isotope fractionation.The nuclear field shift effect is related to the difference in ground-state electronic energies caused by the difference in nuclear size and shape.For the isotope exchange reaction Eq.（1），the NFSE（i.e.，lnKfs）is written as（e.g.，Bigeleisen 1996） where E0is the ground-state electronic energy；AX and A′X represent compounds with different isotopes.Equation（7）shows that the NFSE value is proportional to 1/T，while the MDEscaleswith1/T2（Eq.（5））.Ifthetemperatureisatconstant，the values of the NFSE will be proportional to the difference in ground-stateelectronicenergiescausedbyisotopesubstitutions.

The effect of nuclear field shift is also considered to be proportional to the electron density at the nucleus（King 1984）.The electron density at the nucleus is expressed as |Ψ（0）|2（also called contact density）：

where δEfsis the difference in NFSE-driven ground-state energies；δ＜r2＞is the difference in mean-square nuclear charge radii of the two isotopic nuclei；i and j represent the heavy and light isotopes.

4 Mass-independent fractionation（MIF）

Mass-independent fractionation refers to the deviation from the mass-dependent isotope fractionation line.Taking Hg isotopes as an example，the δiHg is defined as

and the MIF of any pair of Hg isotopes（e.g.，iHg/198Hg）becomes where2002； Young et al.2002），and λMDis the conventional massdependent scaling factor.

Unfortunately，the ΔiHg values cannot be obtained through theoretical methods because the values of δ202Hgfor a fractionation species cannot be calculated.Instead of the absolute value of ΔiHg for species A or B，the relative MIFofspeciesAcomparingwithspeciesB （i.e.，ΔiHgA-B）can be calculated，thus：

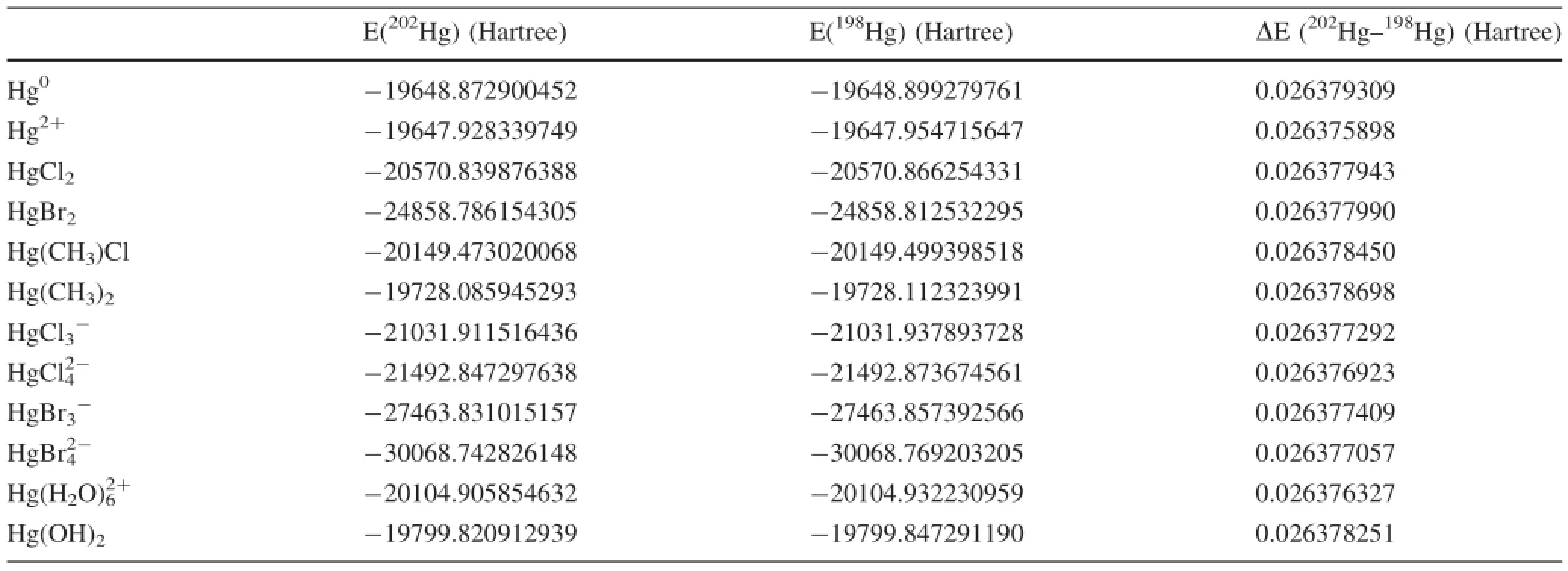
Table 1 Calculated total energies（i.e.，electron energies plus nuclear repulsion energies）of mercury atoms，ions，and molecules

Therefore，the mass-independent fractionation between species A and B is

where λNFSis the nuclear field shift scaling factor；λMIEis the magnetic isotope effect scaling factor；λOtheris any other scaling factors and lnαotheris fractionation driven by other causes except the MDE，the NFSE and the MIE.Here if only the MIF caused by the NFSE is considered，it would be

where λMDis calculated using the high temperature approximation of equilibrium fractionation（Young et al. 2002）.Because the values of λMDare weakly temperaturedependent for heavy element isotope systems（Cao and Liu 2011），we have，

and λNFSis from the mean square nuclear charge radii （Schauble 2007）：where mi，mjand mkare the masses of isotopes i，j and k， respectively，andand? r

2k?are their mean square nuclear charge radii.

Other equations for calculating the MIF caused by the NFSEwereproposedbyGhoshetal.（2008）（i.e.andYangandLiu（2015）for experiments，where AiNVand λNVare nuclear field shift scaling factors that are equal to λNFS，and AiMDis mass-dependent scaling factors that are equal to λMD.These two equations are reasonable only when the value of δ is caused by the nuclear field shift effect（i.e.，δNFS）.

5 Experimental and theoretical studies for NFSE

5.1Liquid-liquid extraction experiments

Fujii and his coworkers investigated the nuclear field shift effect of stable isotope equilibrium fractionation of various elements by liquid-liquid extraction experiments，including Ti，Zn，Zr，Fe，Gd，Nd，Cr，Sr，Mo，Ru，Te，Cd and Sn and other isotope systems（Fujii et al.1998a，b；Nishizawa et al.1998；Fujii et al.1999a，b，2000，2002；Shibaharaetal.2002a，b；Fujiietal.2006a，b，2008，2009a，b，c；Moynier et al.2009a，b；Fujii et al.2010）.

Equation（8）can be written specifically as follows in the atomic spectra（King 1984）：

Fig.4 The NFSE-driven fractionations of Hg，Tl，Pb and U systems.a Different slopes of 199-MIF vs.201-MIF.b The NFSE-driven fractionations of Hg-bearing species relative to Hg0.HgCl42-＞ HgCl+＞HgOH+＞HgCl2＞HgClOH＞HgSHCl＞Hg（OH）2＞Hg SMeCl＞Hg（SH）+＞HgSHOH＞Hg（SH）2＞HgSMeOH＞Hg（Sme）2＞Hg（Sme）+，at 25°C（Wiederhold et al.2010）.Schauble（2013）calculate the NFSE in Hg crystals［HgO（s）＞HgS（s）＞Hg2Cl2（s）＞Hg2Cl2（g）＞β-Hg（s）＞fcc-Hg（s）＞α-Hg（s）＞bcc-Hg（s）＞sc-Hg（s）］at 25 and 180°C. c The NFSEs-driven fractionations of Tl-bearing species relative to Tl0.Fujii et al.（2013）only calculated the NFSEs at 25°C［Tl3+＞Tl（H2O）3+＞TlO-＞TlCl＞0＞TlO+＞Tl+＞Tl（H2O）+＞TlCl2+］.d The NFSE-driven fractionations of the Pb-bearing species，relative to Pb0（Yang and Liu 2015），and Pb2+（Fujii et al.2011a，b）.Fujii et al.（2011a）only estimates the NFSEs at 25°C［PbO＞Pb0＞PbCl+＞Pb（H2O）2+＞0］.e The NFSEs-driven fractionations of the U（III）-U（IV）system at MCDCHF level（Abe et al.2008a），the DCHF method with the Gaussian-type finite-nucleus model using the three basis sets（dz-dz，tz-dz and tz-dz）（Abe et al.2008b）and one experimental result（2.7）（Dujardin and Lonchampt 1992；Lerat and Lorrain 1985）at 293 K.f The NFSE-driven fractionations of the U（IV）-U（VI）system at 308 K.Abe et al.（2008b）calculates it using three basis sets，with and without the BSSE corrections，at the DCHF level with the Gaussian nucleus model（NFSE values：BSSE uncorrected dz-dz＞BSSE corrected tz-tz＞BSSE uncorrected tz-tz＞BSSE corrected tz-dz＞BSSE uncorrected tz-dz＞BSSE corrected dz-dz）. The results of Abe et al.（2010）show the NFSE results of U4+-UO2Cl3-=U4+-UO2Cl42-＞UF4-UO2F42-＞UCl4-UO2Cl3-= UCl4-UO2Cl42-＞UBr4-UO2Br42＞U4+-UO22+＞0＞UCl4-UO22+.The corresponding experimental value is 2.24（Fujii et al.2006c）

where f（z）is a known function of z；a0is Bohr radius and z is the atomic number.Therefore，the simplification of the Eq.（19）（Fujii et al.1999a）is

where b is the scaling factor of the nuclear field shift effect.

When the temperature is constant，the lnα0∝Δm/mm′and lnKBOELE∝Δm/mm′can be obtained by the analysis of the second part.Since lnKanhcan be neglected，Eq.（6）can be simplified as follows：

ε≈lnα=a m Δmm′

+bδ＜r2＞+lnKhf（21）

where the first term is the conventional Bigeleisen-Mayer term；the second term is the nuclear field shift effect term；the third term is the nuclear spin term；a and b are scaling factors of these two terms.The isotope fractionation factor α can be obtained from experiments［i.e.，α=（A/A′）AY/ （A/A′）AX］.The mean square of the charge distribution radii of the nuclei are available from previous studies（e.g.，Fricke and Heilig 2004；Angeli 2004）.Thus，Eq.（21）has three unknown parameters，a，b and lnKhf.

Fujii and coworkers used the isotope pairs to calculate the scaling factors and the nuclear spin effect.For example，for titanium isotopic equilibrium fractionation（Fujii et al. 1998a），they used three isotope pairs，48Ti-46Ti，48Ti-47Ti and48Ti-50Ti.Thus，they got three equations，

Fig.4 continued

They obtained εi-jvalue from experiments and got the＜r2＞i，jvalue from the previous literatures，and calculated a，b and lnKhffrom the above three equations，where i and j represent isotopes 46，47，48 and 50.

5.2Liquid-vapor evaporation experiments

1)碎片化严重。由于现代交通网络的建设，使原有森林古道被割裂或直接被覆盖，残留部分原有道路。未受到现代交通网络影响，但处于偏远地区的森林古道，也逐渐受到人为损毁或直接被遗弃遭受自然侵蚀，造成森林古道碎片化严重，被割裂而存在于各个角落。还有部分森林古道被改造成水泥台阶，致使其深厚的历史底蕴消失，现代化痕迹严重。

There is another type of experiment of liquid-vapor evaporation for studying the nuclear field shift effect. Estrade et al.（2009）and Ghosh et al.（2013）conducted liquid-vapor evaporation experiments in the absence of light for mercury.They both concluded that the nuclear field shift effects are the dominant cause of equilibrium stable isotope fractionation in the absence of light.In addition，experiments were conducted to estimate the massindependent fractionation of Hg isotopes during abiotic reduction（Bergquist and Blum 2007；Zheng and Hintelmann 2010a）and photoreduction in natural water（Zheng and Hintelmann 2009）.They observed that199Hg and201Hg are enriched in the reactant Hg（II）due to the MIF caused by photo-reduction，while the product Hg0enrich199Hg and201Hg where the MIF observed in the absence of light.Zheng and Hintelmann（2010b）also investigated the isotope fractionation of mercury during photochemical reduction by low-molecular-weight organic compounds. They observed the nuclear shift effect in the photochemical reduction by serine.

Estrade et al.（2009）found that MIFs for odd isotopes （199Hg and201Hg）and small MIFs for even isotope（200Hg）in the vapor phase（Hg0）are caused by the NFSE in the temperature range of 2-22°C.Their average results ofHgHg andHg values are 0.1 2‰，0.07‰ and 0.01‰for Hg0，respectively.The results of equilibrium evaporation experiments of Ghosh et al.（2013）are similar to those of Estrad et al.（2009）and their averageHgHg andHg values for Hg0are 0.14‰±0.01‰，0.09‰±0.01‰and0.01‰±0.03‰，respectively.Taking the error into account， there is almost no mass-independent fractionation for the even isotope（200Hg）.

Wiederhold et al.（2010）also investigated the mercury mass-independent fractionations experimentally and theoretically.ItisfoundthattheHg scales withHgina slope of 1.51（Wiederhold et al.2010），1.59（Ghosh et al. 2013），1.61（ZhengandHintelmann2010a），and2.0（Estrade et al.2009）（Fig.4a）.Moynier et al.（2013）reviewed theisotopicvariations（e.g.，UandTl）causedbythenuclearfield shift effect in different natural environments，such as in meteorites and at low-or high-temperatures.

5.3Theoretical calculations of NFSE

5.3.1NFSE in gaseous and small liquid species

Schauble（2007）is the first to perform quantum chemistry calculations of the equilibrium isotope fractionation factors with the consideration of the NFSE.He studied mercuryand thallium-bearing species with the revision of the Bigeleisen-Mayer equation，including the mass-dependent isotope fractionation and the nuclear field shift isotope fractionation.He directly calculated the ground-state electronic energies of isotopic substitution through the Gaussian exponent ξ（ξ=3/2＜r2＞）using the mean square nuclear charger radii of Angeli（2004）by the Dirac 04 software package and obtained the values of the NFSE by Eq.（7）.

Schauble（2007）optimized the molecular geometries at a pseudo-potential HF level by using Gaussian 03.Then he used the optimized geometry results as initial guesses for the second run of optimization in Dirac 04.He used the all-electron Dirac-Hartree-Fock theory to calculate the relativistic electron structures through the iteratively quadratic fitting method，i.e.，to optimize the structures to their lowest energy points by adjusting the bond length stepwise，because the species in his study are all in high symmetry.His calculations indicated that the isotopic variation in the nuclear field shift is the dominant cause of equilibriumfractionation， driving205Tl/203Tland202Hg/198Hg fractionations up to 3‰ at room temperature.But mass-dependent fractionations are much smaller than the NFSE，only ca.0.5‰-1‰ for the same isotopes.

So far，there have been only a few NFSE-included fractionation factors that are determined by theoretical calculations，such as those for uranium，lead，mercury and thallium isotopes（Abe et al.2008a，b，2010；Fujii et al. 2011a；Schauble 2007；Wiederhold et al.2010；Ghosh et al. 2013；Fujii et al.2013；Yang and Liu 2015）（Fig.4b-f）. These authors all found that the nuclear field shift effect was the dominant controlling factor for isotope fractionation of the heavy elements，far more important than the conventional mass-dependent effects.Anomalous light isotope enrichments of U（IV），U（VI），Pb（II）and Tl（I）relative to U（III），U（IV），Pb0and Tl0were found（Schauble 2007；Abe et al.2008a，b，2010；Fujii et al.2011a，2013；Yang and Liu 2015）.In addition，zinc（Fujii et al. 2009c，2010）and nickel isotopes（Fujii et al.2011b）were studied both experimentally and theoretically.However， the NFSE was found to be much smaller than the conventional mass-dependent effects for their cases.

The calculation of Schauble（2007），Wiederhold et al. （2010），Ghosh et al.（2013）and Yang and Liu（2015）all showed that a part of the MIFs of Hg-bearing species are caused by the nuclear field shift effect.These authors found that the NFSE-driven MIFs of odd mass number isotopesHg andHg）are largerthan that of the even mass n umber isotopeHg）.Plotting the Δ1N9F9SH g againstHg，all the data fall into a straight line with the slope of 1.65（Wiederhold et al.2010），or 1.66（Yang and Liu 2015）if using the nuclear charge radii of Fricke and Heilig （2004）.It agreed well with the experimental results. However，the results would deviate far away from the experimental slopes when other nuclear charge radii are used，such as the slope of 2.7［＜r2＞values are from Angeli（2004）］，and 2.5（＜r2＞from Hahn et al.1979）（Fig.4a），showing the nuclear charge radii from Fricke and Heilig（2004）are more reasonable for the Hg-NFSE the-oretical investigation.The slope ofHg/Hg only relates to the conventional mass-dependent scaling factor（i.e.，λMD）and the nuclear field shift scaling factor（i.e.，λNFS）.It is independent of the absolute values of Hg andHg，and the variation in temperature.Therefore，the slope will be a constant value of 1.64（without rounding off the numbers）when the radii of the Landolt-Boernstein Database（Fricke and Heilig 2004）are used as the temperature varies from 0°C to 1000°C or even higher.

The results of200Hg-MIF caused by the NFSE of Yang and Liu（2015）exclude the nuclear field shift from the causes of large200Hg-MIF found in the field observations of Gratz et al.（2010）and Chen et al.（2012）.The results of snow sample from subarctic zone are much larger and in opposite directions（Chen et al.2012）.Therefore，there mustbeothermechanismstoproducesuchlarge200Hg-MIF signals instead of the NFSE.Yang and Liu （2015）also investigates the NFSE-driven MIFs of Pbbearing species.They found that the magnitudes of odd mass number MIFPb）are almost equal to those of even mass numberMIFPb）but in opposite directions（i.e.，Pb≈-Pb）.

5.3.2NFSE in crystals

The theoretical treatment of the NFSE requires quantum mechanics methods that can deal with relativistic quantum effects.Therefore，the Dirac equation-based methods are usually used.It is different from the Schro¨dinger equationbased methods for non-relativistic quantum chemistry calculations.The inner electrons（e.g.，in s and p orbitals）of heavy elements run fast enough to produce largerelativistic effects.The outer electrons also have indirect relativistic effects.Both of them need the Dirac equation to deal with.The influences of relativistic effects about atomic structure are various，including the electron orbital contraction caused by the mass variation due to the high velocity and the coupling between electron spin and electron motion.

To date，a few computational methods for the study of quantum relativistic effects in connection with the NFSE are available.For example，the methods of Schauble（2007）and Yang and Liu（2015）take the quantum relativistic effects into account using the four-component Dirac equation in the DIRAC software package，the method of Abe et al.（2008a，b，2010）uses a four-component relativistic atomic program package-GRASP2 K，and the method of Fujii et al.（2011a，b，2013）uses a software providedbyTokyoUniversity（Utchem）.Recently，Nemoto et al.（2015）develop a two-component relativistic method（the finite-order Douglas-Kroll-Hess method with infinite-order spin-orbit interactions for the one-electron term and atomic-mean-field spin-same-orbit interaction for the two-electron term，i.e.，IODKH-IOSO-MFSO）for the NFSE investigation.This method achieves almost equivalent accuracy but 30 times faster than the previous fourcomponent method by the DIRAC software.The IODKHIOSO-MFSO method has the potential to handle larger systems for the NFSE investigation in the future.However，it is still difficult to calculate the NFSE in crystals due to the relativistic effects of heavy elements.A few softwares，such as ABINIT and VASP，can calculate the properties of large molecules and crystals in the three-dimensional periodic boundary condition but must use pseudopotentials. More accurate methods for calculating the NFSE in very complex systems，such as crystals and melts，are yet to be developed.The methods for these systems need to consider the relativistic effects of heavy elements.

The above NFSE-calculations are only for the gaseous or small liquid species.To date，there is only one paper that reports the nuclear field shift effects in crystalline solids. Schauble（2013）estimated that the all-electron four-component Dirac-Hartree-Fock（DHF）method can be affordable only for systems with less than 20 atoms due to its computation intensity.Therefore，a density functional theory（DFT）based method is developed by Schauble （2013）to model the nuclear field shift effects in crystals. This new method uses the projector augmented wave method（DFT-PAW）with the three-dimensional periodic boundary condition for greater speed and compatibility （Schauble 2013）.

Schauble（2013）compared the contact densities of a few species by the four-component relativistic Dirac-Hartree-Fock（DHF）method and by the DFT-PAW method（with thePerdew-Wangfunctionalinthelocaldensity approximation and the Perdew，Burke，and Ernzerhof functionalinthegeneralized gradientapproximation methods），which are implemented in DIRAC and ABINIT software packages，respectively（Fig.5）.The calculated contact densities by DFT-PAW or DHF method for Hg，Sn-and Cd-bearing species are plotted into the Fig.5a. The two sets of contact densities fall into a regression line with the slope close to 1.0，suggesting they are almost equivalent.

Equation（19）from King（1984）needs non-relativistic contact densities，which is not suitable for heavy elements with strong relativistic effects.Therefore，Schauble（2013）chose not to use Eq.（19）but to figure out a way that can indirectly obtain the energy shift（δT）.He found that there is a good correlation between the contact densities［no matter obtained by DFT-PAW or by DHF）with the energy shifts calculated by the relativistic DHF and coupledcluster（CCSD（T）］methods，where the nuclear charge distributions are varied due to different radii used in the Gaussian function for different isotopes（Fig.5b-d）.His results show that the difference in energies induced by isotope substitution calculated at CCSD（T）level is more strongly correlated with the contact densities of DFT-PAW than that of DHF level.The almost same correlation coefficients are obtained by the DFT-PAW models with PW and PBE functional（Schauble 2013）.The results of Schauble（2013）in mercury crystals are shown in Fig.4b.

5.4Kinetic isotope fractionation of NFSE

When the forward reaction rate of a chemical reaction is much larger than the backward one，the kinetic isotope fractionation effect（KIE）often takes place.The classical transition state theory（TST）is proposed to deal with the elementary one-step reactions（Eyring 1935）.According to the transition state theory，there must be an activated complex formed at the middle of the pathway from the reactant to the product（Fig.6），where is at the highest point along the potential energy curve.The magnitude of the kinetic isotope effect can be calculated by using the theory proposed by Bigeleisen and Wolfsberg（1958），which suggests the KIE is just the equilibrium isotope fractionation between the transition state activated complex and the reactant.Their theory is based on high temperature approximation and neglects possible quantum（tunneling）effects.An empirical rule suggests that a molecule or a substance containing the light isotope will react faster than that containing heavy isotope，leading to the products to be enriched in light isotopes.

All the above experimental and theoretical studies of the NFSE are for equilibrium conditions.Fujii et al.（2009a）predicted if the NFSE-driven MIF in a kinetic system are related to the δ＜r2＞trend，large MIFs can also be found insome reactions.Basu et al.（2014）conducted experiments of U（VI）reduction by bacterial isolates.They found that the reduced U［i.e.，U（IV）］enriches heavier isotopes（238U）in the kinetic reaction similar to the NFSE-driven isotope enrichments under the equilibrium condition which violates the generally accepted empirical rule.They attributed this anomalous isotope enrichment to the nuclear field shift effect.However，no theoretical calculation on the NFSE-driven KIE has been reported to date.

The electrons in s-orbital are important for the nuclear field shift effect which can cause larger electron density at the nucleus than p-，d-，f-orbitals.Heavier isotopes will prefer to be enriched in the species with fewer s electrons or more p，d and f electrons.Therefore，U（IV）enriches heavier isotopes（i.e.，238U）relative to U（VI）in the reduction reaction from U（VI）to U（IV）no matter it is under equilibrium or kinetic conditions，because U（IV）and U（VI）are with the electron configuration as［Rn］5f2and ［Rn］，respectively.This phenomenon is against the general rule that heavier isotopes tend to enrich in the reactant rather than the product in a kinetic reaction.This anomalous enrichment phenomenon will also be for a few heavy elements in a kinetic system because of their smaller s-orbital or more p-，d-，f-orbital electrons，such as Hg0oxidized to Hg（II），Tl0oxidized to Tl（III），Pb0oxidized to Pb（IV），and U（IV）reduced to U（III）.

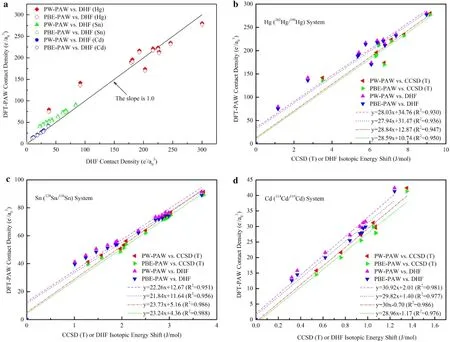
Fig.5 Correlations of calculated contact densities with DFT-PAW methods and relativistic all-electron methods（Schauble 2013）.a Contact densities calculated by DFT-PAW methods against Dirac-Hartree-Fock methods for Hg-，Sn-，and Cd-bearing molecules，respectively.The black line shows ideal 1：1 correlation.b-d Correlations of DFT-PAW contact densities with Dirac-Hartree-Fock（DHF）and coupled-cluster ［CCSD（T）］isotopic energy shifts for202Hg/198Hg relative to Hg2+，124Sn/116Sn relative to Sn4+，and114Cd/110Cd relative to Cd2+，respectively

6 Isotope geochronology

In natural systems，the abundance variations of natural radioisotopes record the geological time，and they are therefore effective tracers for geological processes.Isotopicgeochronology，basedontheaccumulationofradioisotopes with time，is a time keeper for closed geologic systems.Thus，radioisotope tracer can be used to study the genesis and evolution of the earth′s crust，mantle and other celestial bodies.

Fig.6 The classical transition state theory（TST）and the way it deals with a kinetic reaction.There is an activated complex at the highest potential energy place alone the pathway from the reactant to the product（i.e.，transition-state complex）.The figure takes the kinetic reaction of Hg and O3as an example

The base of radioisotope dating is the law of radioactive decayanditmeasurestheisotope compositionsoftheparent and radiogenic daughter.It can be written as（White 2015） where N is the number of atoms of the parent and D is the total number of daughters，at time t；and D0is the original number of daughters.Taking the decay of235U to207Pb as an example，Eq.（25）becomes

In practice，it generally measures the relative ratio of two isotopes，not the absolute abundance of one isotope in experiments.Therefore，Eq.（26）can be written as

where204Pb is non-radiogenic isotope.Other decay systems can be written in similar expressions.

In the past，the accepted invariant value 137.88 of238U/235U ratio was used for U-Pb and Pb-Pb dating. Nowadays，a few researches have verified that238U/235U is not invariable（Stirling et al.2007；Weyer et al.2008；Hiess et al.2012；Goldmann et al.2015；Tissot and Dauphas 2015）.Therefore，an age correction is required if the value of 137.88（238U/235U ratio）is used for dating.Goldmann et al.（2015）found the Pb-Pb ages they dated are 0.9 Ma younger than the age determined with previously assumed value 137.88 for238U/235U.Tissot and Dauphas（2015）proposed equations for the corrections on Pb-Pb and U-Pb ages，although these corrections are much smaller than the ages of the samples.The magnitude and direction of Pb-Pb and U-Pb age corrections are only related to a sample's age and238U/235U ratio.

Many isotope dating methods are available for heavy elements that have large isotopic fractionations caused by the nuclear field shift effect，such as U-Th-Pb，Re-Os，Lu-Hf and Sm-Nd systematics.In these systems，the NFSE-driven fractionation will make the ratio of parent or daughter isotopes vary.It is unclear how the NFSE may affect the isotope age determination.This is an interesting topic for study using theoretical and experimental methods.

7 Summary

The nuclear field shift effect is an inherent property of heavy elements that induces large isotope fractionation.It is a mass-independent isotope fractionation driving force，which is originated from the difference in the ground-state electronic energies caused by differences in nuclear size and shape.The necessity of careful NFSE evaluation during the exploration of new heavy isotope systems is recognized by many researchers.

At different temperatures from 273 to 1000 K，the massdependent effect and the nuclear field shift effect scale as 1/T2and 1/T，respectively.At higher temperatures，the NFSE becomes more important than the MDE.With the rapid progress of experimental techniques and relativistic quantum chemistry，a better understanding of the nuclear field shift effect for heavy elements will emerge.However，there are still many details of the NFSE that need further investigation，such as the kinetic isotope effects（KIE），the NFSE in very large systems（e.g.，solids，melts），and isotope geochronology.

Acknowledgments Y.L.are grateful for the funding support from the 973 Program（2014CB440904）and Chinese NSF projects（41225012，41490635，41530210）.

Open Access ThisarticleisdistributedunderthetermsoftheCreative CommonsAttribution4.0InternationalLicense（http：//creative commons.org/licenses/by/4.0/），which permits unrestricted use，distribution，and reproduction in any medium，provided you give appropriatecredittotheoriginalauthor（s）andthesource，providealink to the Creative Commons license，and indicate if changes were made.

References

Abe M，Suzuki T，Fujii Y，Hada M（2008a）An ab initio study based on a finite nucleus model for isotope fractionation in the U（III）-U（IV）exchange reaction system.J Chem Phys 128：144309-1-144309-6

Abe M，Suzuki T，Fujii Y，Hada M，Hirao K（2008b）An ab initio molecular orbital study of the nuclear volume effects in uranium isotope fractionations.J Chem Phys 129：164309-1-164309-7

Abe M，Suzuki T，Fujii Y，Hada M，Hirao K（2010）Ligand effect on uranium isotope fractionations caused by nuclear volume effects：An ab initio relativistic molecular orbital study.J Chem Phys 133：044309-1-044309-5

Angeli I（2004）A consistent set of nuclear rms charge radii：properties of the radius surface R（N，Z）.Atom Data Nucl Data Tables 87：185-206

Aufmuth P，Heilig K，Steudel A（1987）Changes in mean-square nuclear charge radii from optical isotope shifts.Atom Data Nucl Data Tables 37：455-490

Basu A，Sanford RA，Johnson TH，Lundstrom CC，LO¨ffler FE（2014）Uranium isotopic fractionation factors during U（VI）reduction by bacterial isolates.Geochim Cosmochim Acta 136：100-113

Bergquist BA，Blum JD（2007）Mass-dependent and-independent fractionation of Hg isotopes by photoreduction in aquatic systems.Science 318：417-419

Bigeleisen J（1996）Nuclear size and shape effects in chemical reaction.Isotope chemistry of the heavy elements.J Am Chem Soc 118：3676-3680

Bigeleisen J（1998）Second-order correction to the Bigeleisen-Mayer equation due to the nuclear field shift.Proc Natl Acad Sci USA 95：4809-4908

Bigeleisen J，Mayer MG（1947）Calculation of equilibrium constants for isotopic exchange reactions.J Chem Phys 15：261-267

Bigeleisen J，Wolfsberg M （1958）Theoretical and experimental aspects of isotope effects in chemical kinetics.Adv Chem Phys 1：15-76

Cao XB，Liu Y（2011）Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes.Geochim Cosmochim Acta 75：7435-7445

Chen JR，Nomura M，Fujii Y，Kawakami F，Okamoto M （1992）Gadolinium isotope separation by cation exchange chromatography.J Nucl Sci Technol 29：1086-1092

Chen JB，Hintelmann H，Feng XB，Dimock B（2012）Unusual fractionation of both odd and even mercury isotopes in precipitation from Peterborough，ON，Canada.Geochim Cosmochim Acta 90：33-46

Dujardin T，Lonchampt G（1992）In：Fujii Y，Ishida T，Takeuchi K （eds），Uranium enrichment，Proceedings of international symposium on isotope separation and chemical exchange.Bull Res Lab Nucl React，Tokyo Institute of Technology，Tokyo

Estrade N，Carignan J，Sonke JE，Donard OFX（2009）Mercury isotope fractionation during liquid-vapor evaporation experiments.Geochim Cosmochim Acta 73：2693-2711

Eyring H （1935）The activated complex in chemical reactions. J Chem Phys 3：107-115

Fricke G，Heilig K （2004）92-U Uranium.Landolt-Boernstein. Numerical data and functional relationships in science and technology.Group I：element particles，nuclei and atoms. Springer，Heidelberg vol 20，pp 1-5.Nuclear Charge Radii

Fujii Y，Nomura M，Onitsuka H，Takeda K（1989a）Anomalous isotope fractionation in uranium enrichment process.J Nucl Sci Technol 26：1061-1064

Fujii Y，Nomura M，Okamoto M，Onitsuka H，Kawakami F，Takeda K（1989b）An anomalous isotope effect of235U in U（IV）-U（VI）chemical exchange.Z Naturforsch A 44：395-398

Fujii T，Inagawa J，Nishizawa K（1998a）Influences of nuclear mass，size，shape and spin on chemical isotope effect of titanium.Ber Burtsenges Phys Chem 102：1880-1885

Fujii T，Yamamoto T，Inagawa J，Watanabe K，Nishizawa K（1998b）Influences of nuclear size and shape and nuclear spin on chemical isotope effect of zirconium-crown complex.Ber Burtsenges Phys Chem 102：663-669

Fujii T，Kawashiro F，Yamamoto T，Nomura M，Nishizawa K（1999a）Contribution of nuclear size and shape to chemical enrichment of iron isotopes.Solv Extr Ion Exch 17：177-190

Fujii T，Yamamoto T，Inagawa J，Gunji K，Watanabe K，Nishizawa K （1999b）Nuclear size and shape effect in chemical isotope effect of gadolinium using dicyclohexano-18-crown-6.Solv Extr Ion Exch 17：1219-1229

Fujii T，Yamatomo T，Inagawaa J，Gunji K，Watanabe K，Nishizawa K（2000）Nuclear size and shape effects in chemical isotope enrichment of neodymium using a crown ether.SolvExtr Ion Exch 18：1155-1166

Fujii T，Suzuki D，Gunji K，Watanabe K，Moriyama H，Nishizawa K （2002）Nuclear field shift effect in the isotope exchange reaction of chromium（III）using a crown ether.J Phys Chem A 106：6911-6914

Fujii T，Moynier F，Albarede F（2006a）Nuclear field vs.nucleosynthetic effects as cause of isotopic anomalies in the early Solar System.Earth Planet Sci Lett 247：1-9

Fujii T，Moynier F，Telouk P，Albarede F（2006b）Mass-independent isotope fractionation of molybdenum and ruthenium and the originofisotopicanomaliesinMurchison.AstrophysJ 647：1506-1516

Fujii Y，Higuchi N，Haruno Y，Nomura M，Suzuki T（2006c）Temperature dependence of isotope effects in uranium chemical exchange reactions.J Nucl Sci Technol 43：400-406

Fujii T，Suzuki D，Yamana H（2008）Nuclear field shift effect of chromium（III）in repeated extraction using a crown ether.Solv Extr Ion Exch 26：100-112

Fujii T，Moynier F，Albarede F（2009a）The nuclear field shift effect in chemical exchange reactions.Chem Geol 267：139-156

Fujii T，Moynier F，Telouk P，Albarede F（2009b）Nuclear field shift effect in the isotope exchange reaction of cadmium using a crown ether.Chem Geol 267：157-163

Fujii T，Moynier F，Uehara A，Abe M，Yin QZ，Nagai T，Yamana H（2009c）Mass-dependentandmass-independentisotope effectsofzincinaredoxreaction.JPhysChemA 113：12225-12232

Fujii T，Moynier F，Telouk P，Abe M （2010）Experimental and Theoretical Investigation of Isotope Fractionation of Zinc between Aqua，Chloro，and Macrocyclic Complexes.J Phy Chem A 114：2543-2552

Fujii T，Moynier F，Agranier A，Ponzevera E，Abe M（2011a）Nuclear field shift effect of lead in ligand exchange reaction using a crown ether.Proc Radiochim Acta 1：387-392

Fujii T，Moynier F，Dauphas N，Abe M （2011b）Theoretical and experimental investigation of nickel isotopic fractionation in species relevant to modern and ancient oceans.Geochim Cosmochim Acta 75：469-482

Fujii T，Moynier F，Agranier A，Ponzevera E，Abe M，Uehara A，Yamana H（2013）Nuclear field shift effect in isotope fractionation of thallium.J Radioanal Nucl Chem 296：261-265

Ghosh S，Xu XF，Humayun M，Odom L（2008）Mass-independent fractionation of mercury isotopes in the environment.Geochem Geophy Geosy 9：Q03004.doi：10.1029/2007GC001827

Ghosh S，Schauble EA，Couloume GL，Blum JD，Bergquist BA （2013）Estimation of nuclear volume dependent fractionation of mercury isotopes in equilibrium liquid-vapor evaporation experiments.Chem Geol 336：5-12

Goldmann A，Brennecka G，Noordmann J，Weyer S，Wadhwa M （2015）The uranium isotopic composition of the Earth and the Solar System.Geochim Cosmochim Acta 148：145-158

Gratz LE，Keeler GJ，Blum JD，Sherman LS（2010）Isotopic composition and fractionation of mercury in great lakes precipitation and ambient air.Environ Sci Technol 44：7764-7770

Hahn AA，Miller JP，Powers RJ，Zehnder A，Rushton AM，Welsh RE，Kunselman AR，Roberson P（1979）Experimental-study of muonic X-ray transitions in mercury isotopes.Nucl Phys 314：361-386

Heilig K，Steudel A（1978）In：Hanel W，Kleinpoppen H（eds）Progress in atomic spectroscopy，part A.Plenum Press，New York，pp 263-328

Hiess J，Condon DJ，McLean N，Noble SR（2012）238U/235U systematics in terrestrial uranium-bearing minerals.Science 335：1610-1614

King WH（1984）Isotope shifts in atomic spectra.Plenum Press，New York

Kleinman LI，Wolfsberg M（1973）Corrections to the Born-Oppenheimerapproximationandelectroniceffectsonisotopic exchange equilibria.Chem Phys 59：2043-2053

Kleinman LI，Wolfsberg M （1974）Corrections to the Born-Oppenheimerapproximationandelectroniceffectsonisotopic exchange equilibria.2.Chem Phys 60：4740-4748

Lerat JM，Lorrain C（1985）Solvent extraction and ion exchange in the nuclear fuel cycle.Soc Chem Ind，Ellis Horwood Ltd.，London

Miller MF（2002）Isotopic fractionation and the quantification of O-17 anomalies in the oxygen three-isotope system：an appraisal andgeochemicalsignificance.GeochimCosmochimActa 66：1881-1889

Moynier F，Fujii T，Albare`de F et al（2009a）Nuclear field shift effect as a possible cause of Te isotopic anomalies in the early solar system-an alternative explanation of Fehr et al.2006-2009. Meteorit Planet Sci 44：1735-1742

Moynier F，Fujii T，Telouk P（2009b）Mass-independent isotope fractionation of tin in chemical exchange reaction using a crown ether.Anal Chim Acta 632：234-239

Moynier F，Fujii T，Brennecka GA，Nielsen SG（2013）Nuclear field shift in natural environments.C R Geoscience 345：150-159

Nemoto K，Abe M，Seino J，Hada M（2015）An ab intio study of nuclear volume effects for isotope fractionations using twocomponent relativistic methods.J Comput Chem 36：816-820

Nishizawa K，Nakamura K，Yamamoto T，Masuda T（1993）Zinc isotope effects in complex-formation with a crown-ether.Solv Extr Ion Exch 11：389-394

Nishizawa K，Nakamura K，Yamamoto T，Masuda T（1994）Separation of strontium and barium isotopes using a crownether.Different behaviors of odd mass and even mass isotopes. Solv Extr Ion Exch 12：1073-1084

Nishizawa K，Satoyama T，Miki T，Yamamoto T（1995）Strontium isotope effect in liquid-liquid extraction of strontium chloride using a crown ether.J Nucl Sci Technol 32：1230-1235

Nishizawa K，Maeda Y，Kawashiro F，Fujii T，Yamamoto T（1998）Contributions of nuclear size and shape，nuclear spin to enrichment factors of zinc isotopes in a chemical exchange reaction by a cryptand.Separ Sci Technol 33：2101-2112

Nomura M，Higuchi N，Fujii Y（1996）Mass dependence of uranium isotope effects in the U（IV）-U（VI）exchange reaction.J Am Chem Soc 118：9127-9130

Schauble EA（2007）Role of nuclear volume in driving equilibrium stable isotope fractionation of mercury，thallium，and other veryheavyelements.GeochimCosmochimActa 71：2170-2189

Schauble EA（2013）Modeling nuclear volume isotope effects in crystals.Proc Natl Acad Sci USA 110：17714-17719

Shibahara Y，Nishizawa K，Yasaka Y，Fujii T（2002a）Strontium isotope effect in dmso-water system by liquid chromatography using a cryptand polymer.Solv Extr Ion Exch 20：67-79

Shibahara Y，Takaishi H，Nishizawa K，Fujii T（2002b）Strontium isotope effects in ligand exchange reaction.J Nucl Sci Technol 39：451-456

Stacey DN（1966）Isotope shifts and nuclear charge distributions.Rep Prog Phys 29：171-215

Stirling C，Andersen MB，Potter EK，Halliday AN（2007）Lowtemperature isotopic fractionation of uranium.Earth Planet Sci Lett 264：208-225

Tissot FLH，Dauphas N（2015）Uranium isotopic compositions of the crust and ocean：Age corrections，U budget and global extent of modern anoxia.Geochim Cosmochim Acta 167：113-143

Urey HC（1947）The thermodynamic properties of isotopic substances.J Chem Soc（London）85：562-581

Wang XL，Johnson TM，Lundstrom CC（2015）Low temperature equilibrium isotope fractionation and isotope exchange kinetics betweenU（IV）andU（VI）.GeochimCosmochimActa 158：262-275

Weyer S，Anbar A，Gerdes A，Gordon G，Algeo T，Boyle E（2008）Natural fractionation of238U/235U.Geochim Cosmochim Acta 72：345-359

White WM（2015）Isotope geochemistry.Wiley，Chichester

Wiederhold JG，Cramer CJ，Daniel K，Infante I，Bourdon B，Kretzschmar R（2010）Equilibrium mercury isotope fractionation between dissolved Hg（II）species and thiol-bound Hg.Environ Sci Technol 44：4191-4197

Yang S，Liu Y （2015）Nuclear volume effects in equilibrium stable isotope fractionations of mercury，thallium and lead.Sci Rep 5：12626.doi：10.1038/srep12626

Young ED，Galy A，Nagahara H（2002）Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance.Geochim Cosmochim Acta 66：1095-1104

Zheng W，Hintelmann H（2009）Mercury isotope fractionation during photoreduction in natural water is controlled by its Hg/DOC ratio.Geochim Cosmochim Acta 73：6704-6715

Zheng W，Hintelmann H（2010a）Nuclear field shift effect in isotope fractionation of mercury during abiotic reduction in the absence of light.J Phys Chem A 114：4238-4245

Zheng W，Hintelmann H（2010b）Isotope fractionation of mercury during its photochemical reduction by low-molecular-weight organic compounds.J Phys Chem A 114：4246-4253

30 March 2016/Revised：9 May 2016/Accepted：12 May 2016/Published online：15 June 2016

✉ Yun Liu liuyun@vip.gyig.ac.cn
1State Key Laboratory of Ore Deposit Geochemistry，Institute of Geochemistry，Chinese Academy of Sciences，Guiyang 550081，China
2University of Chinese Academy of Sciences，Beijing 100049，China