一种重型燃气轮机建模及其参数估计的方法

黄玉柱，　蒋洪德

(清华大学 燃气轮机与煤气化联合循环国家工程研究中心，北京 100084)



一种重型燃气轮机建模及其参数估计的方法

黄玉柱，蒋洪德

(清华大学 燃气轮机与煤气化联合循环国家工程研究中心，北京 100084)

为研究燃气轮机系统动态特性，基于Rowen模型建立了燃气轮机及其控制系统的数学模型，利用燃气轮机现场运行数据，运用质量守恒、能量守恒和动量守恒原理以及热力学和传热学等基本公式，推算和估计模型的相关参数.以GE MS6001FA型燃气轮机为研究对象，给出燃气轮机建模及参数估计的具体方法和过程。结果表明：该模型能够正确反映燃气轮机的动态特性，符合机组运行规律，具有很好的研究和参考价值.

燃气轮机； Rowen模型； 参数估计； 现场运行数据

近年来，我国电力工业迅猛发展，电网峰谷差日趋增大以及能源结构调整使得燃气轮机及其联合循环发电快速发展[1].借助计算机技术，建立燃气轮机系统模型并进行数字仿真逐渐成为研究其动态特性最有效的手段[2-5].在燃气轮机建模中，最常用的模型为Rowen模型[6-8]，作为一类重要的简化模型，其从控制角度提出了一种新的燃气轮机建模思路，摆脱了传统的用微分方程组表示燃气轮机动态特性的方法，同时借鉴了模块化建模思想，以方块图表示系统数学模型，将各环节用不同方块单元来表示，然后串联起来形成燃气轮机整体模型，使得模型的扩充、简化和维护都很方便，具有较好的模型精度[9-10].然而，Rowen模型并未给出模型参数的具体含义和参数估计的方法[7-8].

笔者给出燃气轮机模型参数的具体含义，并利用现场运行数据，运用质量守恒、能量守恒和动量守恒原理以及热力学和传热学等基本公式推算和估计模型相关参数.同时以GE MS6001FA型燃气轮机为研究对象，基于现场运行数据，给出燃气轮机建模和参数估计的具体方法及过程.

1　燃气轮机系统分析

燃气轮机主体结构主要由压气机、燃烧室、透平和转轴组成.燃气轮机正常工作时，工质依次经过吸气压缩、燃烧加热、膨胀做功和排气放热4个阶段，完成由热变功的热力循环.具体过程如下：由压气机将空气压缩到一定压力，送到燃烧室与燃料掺混燃烧，产生高温高压的燃气，高温高压燃气从燃烧室流入透平，并在透平中膨胀做功，最后燃气压力下降，排至大气中.透平产生的功一部分用于驱动压气机，其余部分用以带动负载，如推动与燃气轮机同轴的发电机发电.在结构上，燃气轮机主要分为重型燃气轮机和航改型燃气轮机，笔者主要讨论单轴重型燃气轮机，其结构如图1所示.

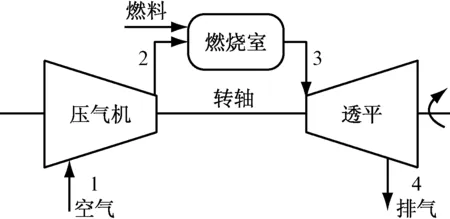
1-压气机入口；2-压气机出口；3-燃烧室出口(透平入口)；4-透平出口.

图1单轴重型燃气轮机结构示意图

Fig.1Schematic structure of a typical single-shaft gas turbine

燃气轮机简单循环热力过程如图2所示，其中1～2s表示压气机的等熵压缩过程，2s～3表示燃烧室内的等压燃烧过程，3～4s表示透平的等熵膨胀过程，4s～1表示排入大气后的等压冷却过程.而实际燃气轮机循环中压缩过程(1～2)和膨胀过程(3～4)都不是等熵的，使得实际压缩功大于等熵压缩功，实际膨胀功小于等熵膨胀功，即压气机等熵效率ηc和透平等熵效率ηt均小于1.在实际燃烧过程中，由于存在不完全燃烧和散热损失，燃烧室燃烧效率ηb小于1.通常，散热损失很小，可忽略，即ηb取决于不完全燃烧的程度.

图2　燃气轮机简单循环温-熵图

2　燃气轮机建模及参数估计

基于Rowen模型，建立简单循环燃气轮机及其控制系统数学模型，如图3所示.考虑到在简单循环下，入口可转导叶(IGV)只在机组启停过程中进行调整，而在正常运行下，IGV将保持最大开度；只有在燃气-蒸汽联合循环时需要调整IGV开度来调节压气机流量，以保持燃气轮机出口温度不变，进而保证部分负荷下联合循环仍能获得较高效率.故在简单循环下，暂不考虑IGV的控制.

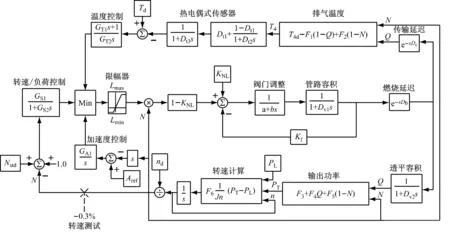
图3　燃气轮机及其控制系统的数学模型

2.1燃气轮机建模及参数估计

燃气轮机模型主要包括温度模块、燃烧模块、功率模块和转子模块.下文将详细给出各模块建模及参数估计的方法.

根据图2，压气机等熵效率ηc和透平等熵效率ηt分别为

(1)

(2)

式中：hi、Ti分别为图2中燃气轮机简单循环在i(i=1,2,2s,3,4,4s)处空气(或燃气)的焓值和温度，kJ/kg和K.

图2中1～2s和3～4s的等熵(可逆绝热)过程初、终态参数的关系可由理想状态方程及绝热过程方程求得.

(3)

(4)

式中：p1、p2、p3和p4分别为压气机入口、压气机出口、透平入口和透平出口的压力，kPa；πc、πt分别为压气机的压缩比和透平的膨胀比；rc、rh分别为低温段(压气机)和高温段(燃烧室和透平)的比热容比.

在燃烧室内压力损失一般变化不大，可认为总压恢复系数ζb为常数，即p3=ζbp2，于是πt=ζbπc.基于文献[7]～文献[10]，低温段(压气机)和高温段(燃烧室和透平)空气和燃气的比热容和比热容比分别为：cpc=1.005 kJ/(kg·K)，cph=1.157 kJ/(kg·K)，rc=1.4，rh=1.33.进一步可得压气机和透平出口温度T2和T4分别为

(5)

(6)

在燃烧室内，来自压气机的压缩空气与经燃料喷嘴喷入的燃料混合、燃烧，将储藏在燃料中的化学能转化为热能，形成高温高压燃气，进入透平中膨胀做功.按照燃料发热量的定义(燃烧室出口燃气温度降至与入口空气温度相同时所放出的热量等于燃料的发热量)，得到燃烧室的热平衡方程：

(7)

式中：qm,2、qm,f分别为压气机出口空气的质量流量(以下简称压气机出口质量流量)和加入燃烧室的燃料质量流量(以下简称燃料量)，kg/s；T3为燃烧室出口温度，K；QLHV为燃料静比能(即低位发热量)，kJ/kg.

考虑到压气机出口的空气质量流量远大于进入燃烧室的燃料量，近似认为燃烧室出口质量流量qm,3=qm,2+qm,f≈qm,2.一般燃烧效率ηb的取值范围为0.96～0.99，假定ηb=0.99，利用式(7)可得

(8)

在实际中，燃气轮机内质量流量、压力和温度等参数都与其转速密切相关，具有高度复杂的非线性关系.而在Rowen模型中，通过限定燃气轮机转速在额定转速的95%～107%范围内，近似认为燃气轮机各参数与转速的关系可简化为某特定的线性关系.基于此，可推导出燃气轮机排气温度(即透平出口温度T4)和输出功率PT的表达式.在额定转速下，假定压气机出口质量流量qm,2与其ISO条件(即大气压力101.325 kPa，温度 15 ℃，相对湿度60%)下的额定值qm,2d相等，即qm,2=qm,2d，联立式(5)、式(6)和式(8)可得

(10)

式中：Q为实际燃料量qm,f与额定燃料量qm,fd之比；下标d表示ISO条件下对应的燃气轮机额定参数，即设计值.

进一步可得不同转速下排气温度T4：

(11)

式中：N为实际转速n与额定转速nd之比；系数F2表征排气温度T4与转速偏差(1-N)的线性关系，其值约为额定排气温度T4d的0.55～0.65倍.

假定压气机出口质量流量qm,2等于透平出口质量流量qm,4，即qm,2=qm,4，则燃气轮机输出功率PT为

(12)

在额定转速下，假定qm,2=qm,2d，根据式(5)、式(6)、式(8)和式(12)可得

(13)

(15)

进一步可得不同转速下输出功率PT：

(16)

式中：系数F5表征输出功率PT与转速偏差(1-N)的线性关系，其值约为额定功率PTd的0.5～0.67倍.

转子是燃气轮机中主要的惯性环节，用来连接压气机、透平和发电机，完成透平做功的传递.根据动量守恒原理，建立转子动态模型:

(17)

式中：J为转子的转动惯量，kg·m2；PL为负载功率，kW；系数F6=91.282.

如图3所示，建立燃烧延迟环节来反映燃料喷入与燃烧完成之间的延迟，对于当代重型燃气轮机，燃烧延迟系数Db多为ms量级.

2.2控制和测量回路建模及参数估计

在简单循环下，不考虑IGV控制，燃气轮机控制系统数学模型主要包括转速/负荷控制模型、温度控制模型、加速度控制模型及相关测量回路模型.

为了适应不同的负载特性，转速/负荷控制作为最基本的控制回路，主要分为“有差调节”和“无差调节”.燃气轮机发电并网运行时采用“有差调节”，以便对负荷进行调节，转速调节器为比例模块.具体过程是通过调整转速基准值，使得转速基准与实际转速存在偏差，从而改变输出的燃料基准，最终达到调整负荷的目的.当燃气轮机处于独立电网或用于机械驱动时采用“无差调节”，无差调节器为比例积分模块，保证实际转速与参考转速一致.本文所研究的燃气轮机用来并网发电，采用“有差调节”，且对应的不等率取3%～7%，其模型见图3.

温度控制主要限制燃气轮机透平入口温度(即燃烧室出口温度T3)，防止透平超温.实际运行中，由于透平入口温度T3很高，难以长期直接测量和控制，于是通过控制排气温度T4来限制T3.温度调节器为比例积分模块.因此，温度控制回路可近似为比例积分环节，其数学模型见图3.

在某些特殊情况下(如起动加速、甩负荷)，加速度控制能够抑制转子动态超速，保证机组的安全.该控制回路可通过对实际转速微分得到转子加速度，然后将其与参考值进行比较，再进行调节来实现.加速度调节器为积分模块，其数学模型见图3.

为了保证燃气轮机各控制回路能协调一致，每个控制回路要经过最小值选择器后输出最小的燃料基准值(即燃料阀门给定值)，并将其输入燃料伺服系统.控制系统模型相关参数可根据实际控制系统的参数设置得到.

在燃料系统中，通过调整燃料(液体或气体)阀门的位置(开度)来调节进入燃烧室的燃料量.尽管液体与气体燃料阀门调整存在差别，但都是通过阀门位置的闭环反馈控制来实现的，基本原理见图4.燃料阀门调整的控制回路模型如图5所示.对于液体燃料阀门的调整，通过改变旁通燃料来调节进入燃烧室的燃料量，即调整旁通调节阀；其模型参数a和b的值可参考厂商提供的数据，而Kf要保证整个阀门调整回路的增益为1，即Kf=1-a.对于气体燃料阀门的调整，可直接调整燃料通路上阀门开度来调节进入燃烧室的燃料量；其模型参数a=1，Kf=0，b根据厂商提供数据得到.

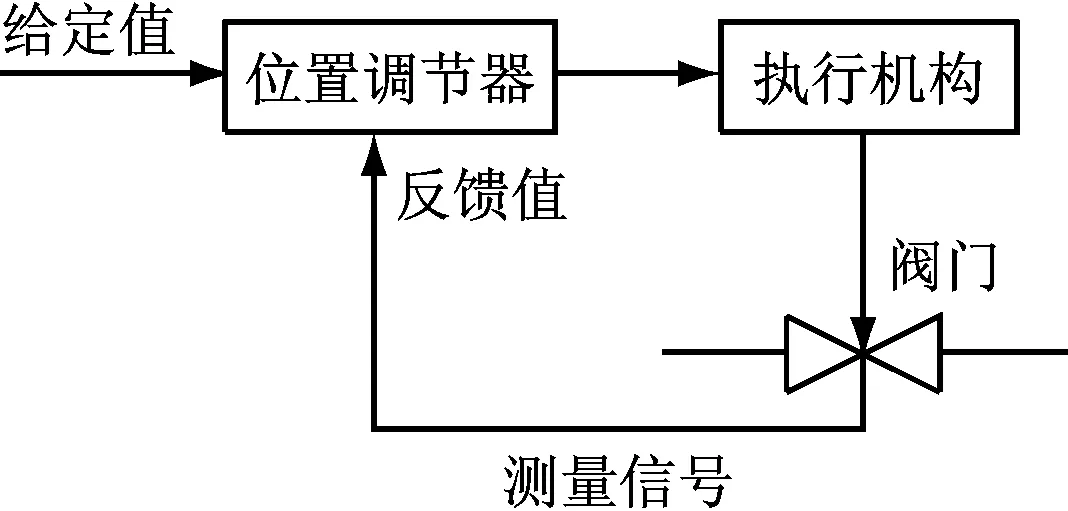
图4　燃料阀门调整原理图

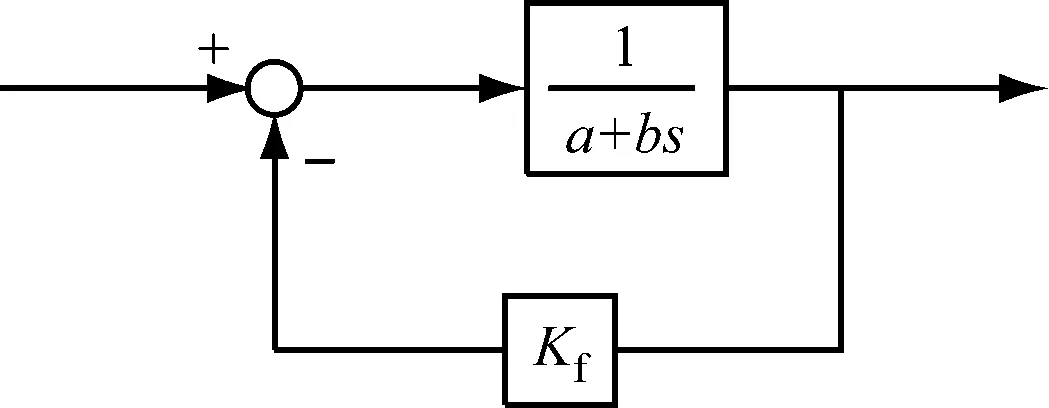
图5　燃料阀门调整的控制回路模型

考虑到燃料相关管路系统的容积特性，当阀门动作后，进入燃烧室的燃料量的变化会存在一定延迟.同理，考虑到透平的容积特性，进入透平的燃气量的变化也会存在延迟.在建模时，通过设置延迟时间来集中反映燃气轮机各部件的容积特性对其质量流量的影响.假定某一部件容积如图6所示，基于流量连续方程，可得容积延迟时间参数Dv为

(18)

(19)

式中：pv为该容积内稳态压力，kPa；qm,v为该容积的稳态质量流量，kg/s；V为容积，m3；v为比体积，m3/kg；Φ为在温度Tv下由压力变化而导致的该容积内密度ρ(ρ=1/v)的变化,kg/m3.

为了计算Φ，假定pv1和pv2分别为该容积内某一较小压力波动产生的前后压力值，v1和v2分别对应pv1和pv2下的比体积，且此期间内Tv保持不变，于是近似可得Φ：

(20)

根据式(18)～式(20)计算得到该容积延迟时间参数Dv.对于气体燃料和工质，由于其可压缩性，比体积变化较大，所以相应的容积延迟时间也会较长.

图6　燃气轮机部件容积示意图

通常采用热电偶式传感器测量得到燃气轮机排气温度.首先，考虑到排气温度测点位置，燃烧室内燃料与空气掺混燃烧形成的高温燃气传输到透平出口温度传感器处需要一定的时间，因此从燃烧放热到传感器测得温度变化过程中存在时间延迟，延迟时间参数Dc取决于重型燃气轮机的尺寸和燃气的平均流速，一般为ms量级.热电偶式传感器的基本结构如图7所示.从图7中传感器测量端的结构可知，热传递过程的影响将导致燃气温度的测量有一定的延迟.基于文献[10]，热电偶式传感器测量端建模如下：

(21)

式中：Tmea和Texh分别为燃气轮机排气温度的测量值和实际值；Dt1、Dt2为该模型相关参数，可由相应的热电偶式传感器结构参数确定.

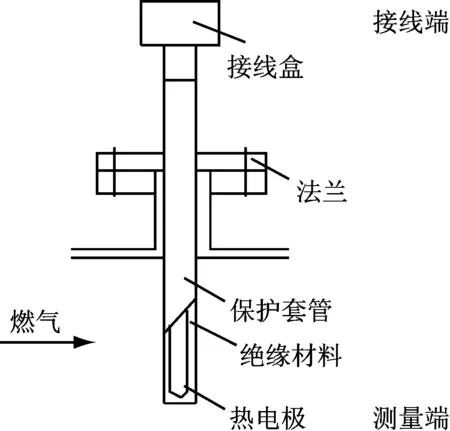
图7　热电偶式传感器结构示意图

考虑到传感器测量处理过程本身具有的延迟特性，存在热电偶式传感器延迟参数Dt3，可通过实际传感器的响应时间确定.

3　GE MS6001FA型燃气轮机建模

信息采集、存储和处理技术的普遍利用和不断发展，使得燃气轮机运行过程中大量生产以及设备和过程数据的收集和存储成为可能，这是燃气轮机建模及参数估计的基础.GE MS6001FA型燃气轮机额定工况(ISO条件)下的性能参数如表1所示.该机组的燃料为天然气，燃气轮机控制系统数学模型如图3所示，其中未考虑IGV的建模.

表2给出了GE MS6001FA型燃气轮机一组典型的现场运行数据.在建模中，机组转速限定为额定转速的95%～107%，并假定压气机等熵效率、燃烧室燃烧效率和透平等熵效率保持不变且均为额定效率值.

表1　GE MS6001FA型燃气轮机额定工况下的性能参数

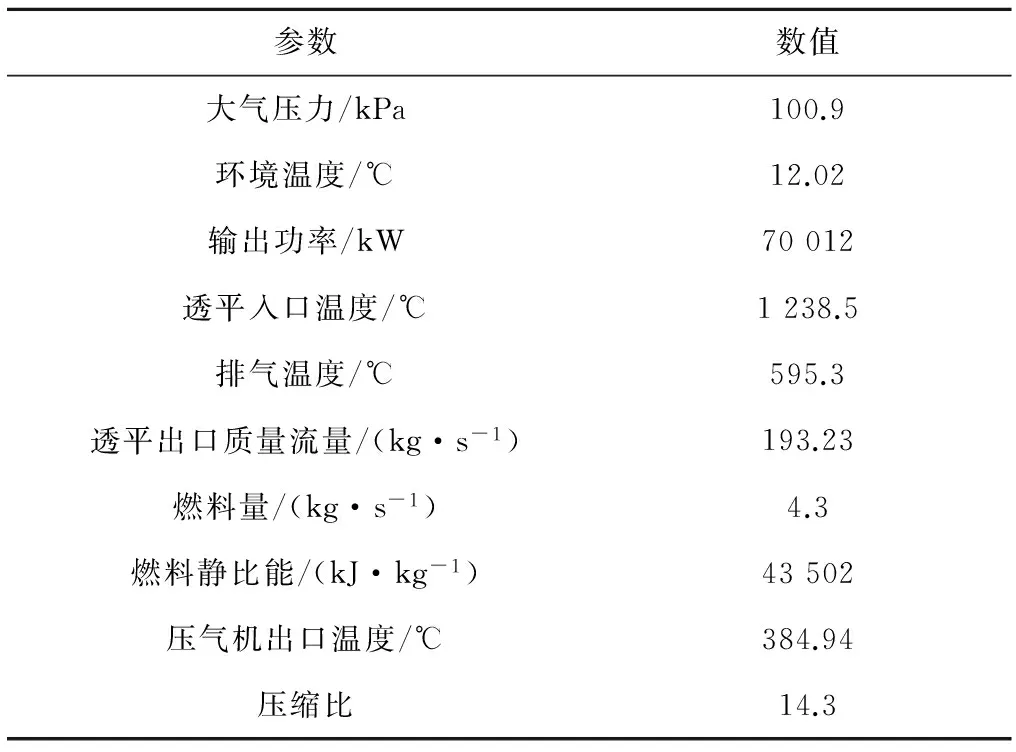
表2　燃气轮机的现场运行数据

关于压气机等熵效率和透平等熵效率，首先假定燃烧室总压恢复系数ζb=0.96，利用表2中数据、式(3)和式(4)，可得压气机和透平等熵出口温度T2s(w)和T4s(w)：

(22)

(23)

式中：下标(w)表示对应表2中该燃气轮机运行值.

利用式(1)和式(22)计算可得ηc=0.87.

同理，基于表2中的数据，利用式(2)和式(23)计算可得ηt=0.89.

由式(14)计算可得F3=-11 308.23.

由式(15)可得

(24)

考虑到额定工况下转速偏差为0且Qd=1，式(12)可简化为

(25)

将F3和F4代入式(30)可得qm,fd=4.64 kg/s，F4=87 178.23.

再由qm,fd和式(10)计算可得F1=457.40.

基于前文分析可知，系数F2和F5分别为

(26)

(27)

至此，模型相关系数F1、F2、F3、F4和F5均可通过计算得到.

关于重型燃气轮机，即使不带负荷，燃气轮机空载运行也需要相当一部分的燃料量.于是在建模中，进入燃烧室的燃料信号为2部分之和，其中一部分为常数KNL，另一部分为(1-KNL)与控制系统输出信号的乘积.如图3所示，控制系统输出要经过一个限幅器L，其最大值Lmax限制燃料过量，防止透平超温；其最小值Lmin为负值，反映透平吸收瞬时功率的能力(逆功率情况).基于表3中燃气轮机空载和最小燃料量数据，计算KNL和Lmin：

(28)

(29)

而Lmax一般为额定燃料量的1.5倍左右，即Lmax=1.5.

表3燃气轮机空载燃料量和最小燃料量

Tab.3No-load and minimum fuel flow of the gas turbine

kg/s

注：1) 燃气轮机空载(不带负荷全速运行)和最小(保证不熄火)燃料量是从现场运行数据中提取和推算出来的，“～”表示推算值.

关于燃料管路系统容积特性，计算其容积延迟时间参数Dv1.首先，基于表4中数据，假设该温度下存在一较小压力波动，并结合理想气体状态方程，根据式(20)可得

(30)

表4　燃料系统相关数据

利用式(18)和式(19)可得Dv1=0.67s.

同理，关于燃烧室及透平的容积特性，计算燃气量变化延迟时间参数Dv2.基于表5中数据，利用式(20)可得

(31)

利用式(18)和式(19)可得Dv2=0.43 s.

根据热电偶式传感器的结构参数测量燃气轮机排气温度，可以确定式(21)中参数Dt1和Dt2；根据实际传感器的响应时间，可以确定热电偶式传感器延迟参数Dt3.在本文中，选取Dt1=0.85、Dt2=12.2和Dt3=1.7.

表5　透平燃气相关数据

图3中所示的燃气轮机控制系统数学模型的相关参数可根据实际控制系统的参数设置得到，具体见表6.

表6　控制系统数学模型参数

注：1)GS1=1/δ，δ为转速调节系统的不等率，取δ=4%.

4　仿真结果与分析

在Matlab/Simlink环境下，基于图3和以上分析得到的模型参数，建立GE MS6001FA型燃气轮机系统模型来模拟其动态特性.下面给出燃气轮机在30%基本负荷(即PL=0.3PTd)下加、减负荷的动态变化情况.首先，基于不等率δ=4%，设定转速基准Nstd的变化曲线(见图8).由图8可知，模拟过程如下：仿真开始50 s内，燃气轮机运行在30%基本负荷下；在50～110 s内加负荷到100%基本负荷，并运行至150 s；在150～170 s内减负荷到70%基本负荷，并运行至210 s；在210～260 s内减负荷到50%基本负荷，运行直至仿真结束.

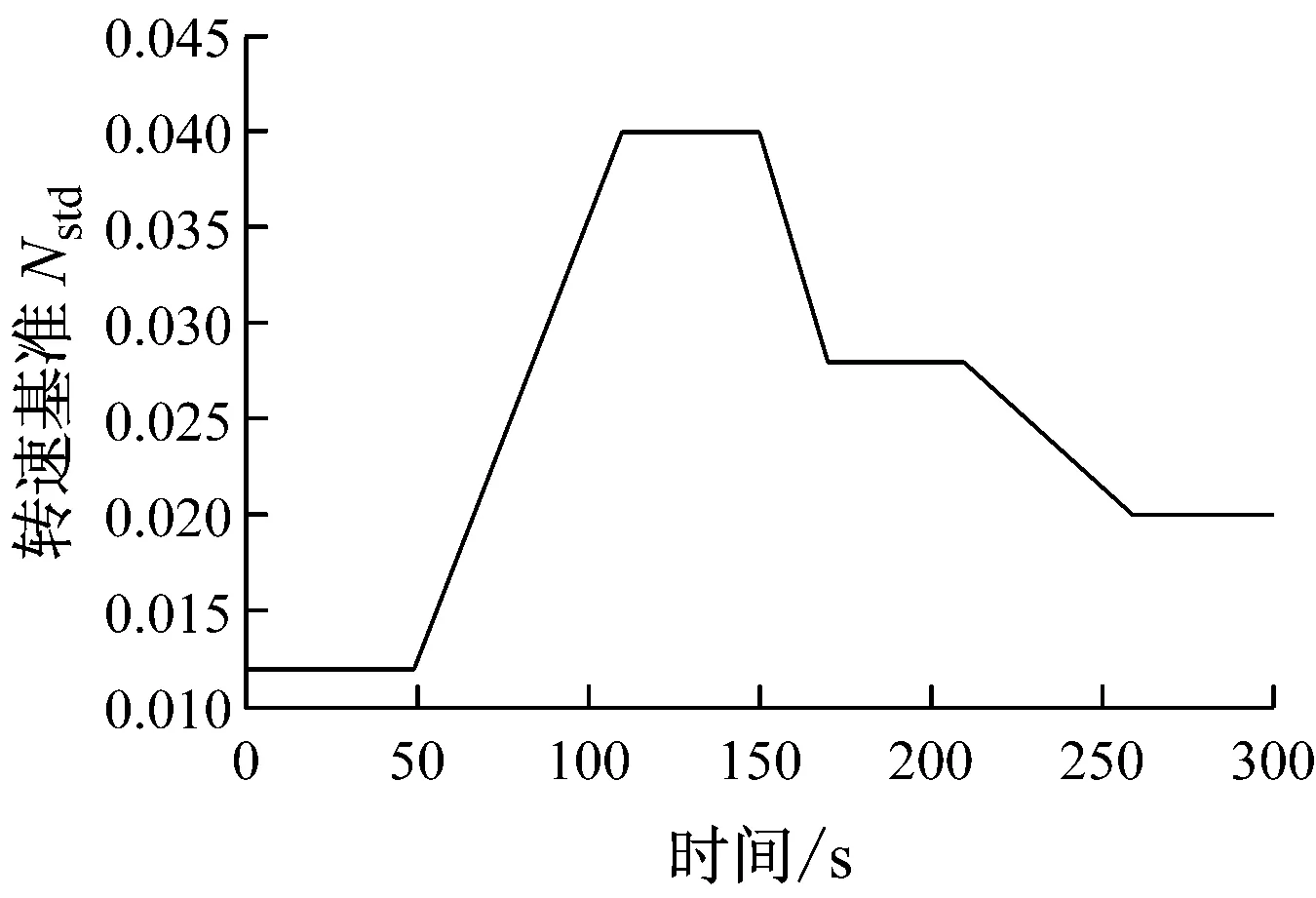
图8　转速基准Nstd曲线

图9～图11给出了燃气轮机加、减负荷过程的模拟结果.由图9～图11可知，随着转速基准Nstd的升、降变化(模拟加、减负荷过程)，燃气轮机排气温度T4、输出功率PT和燃料量qm,f都随之升、降，这与实际过程的变化趋势吻合.

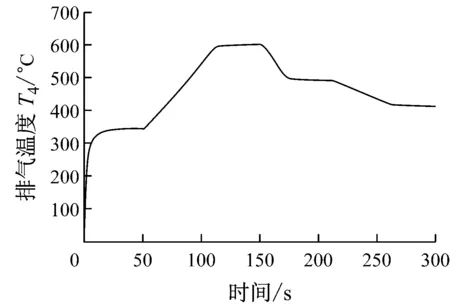
图9　排气温度T4变化曲线

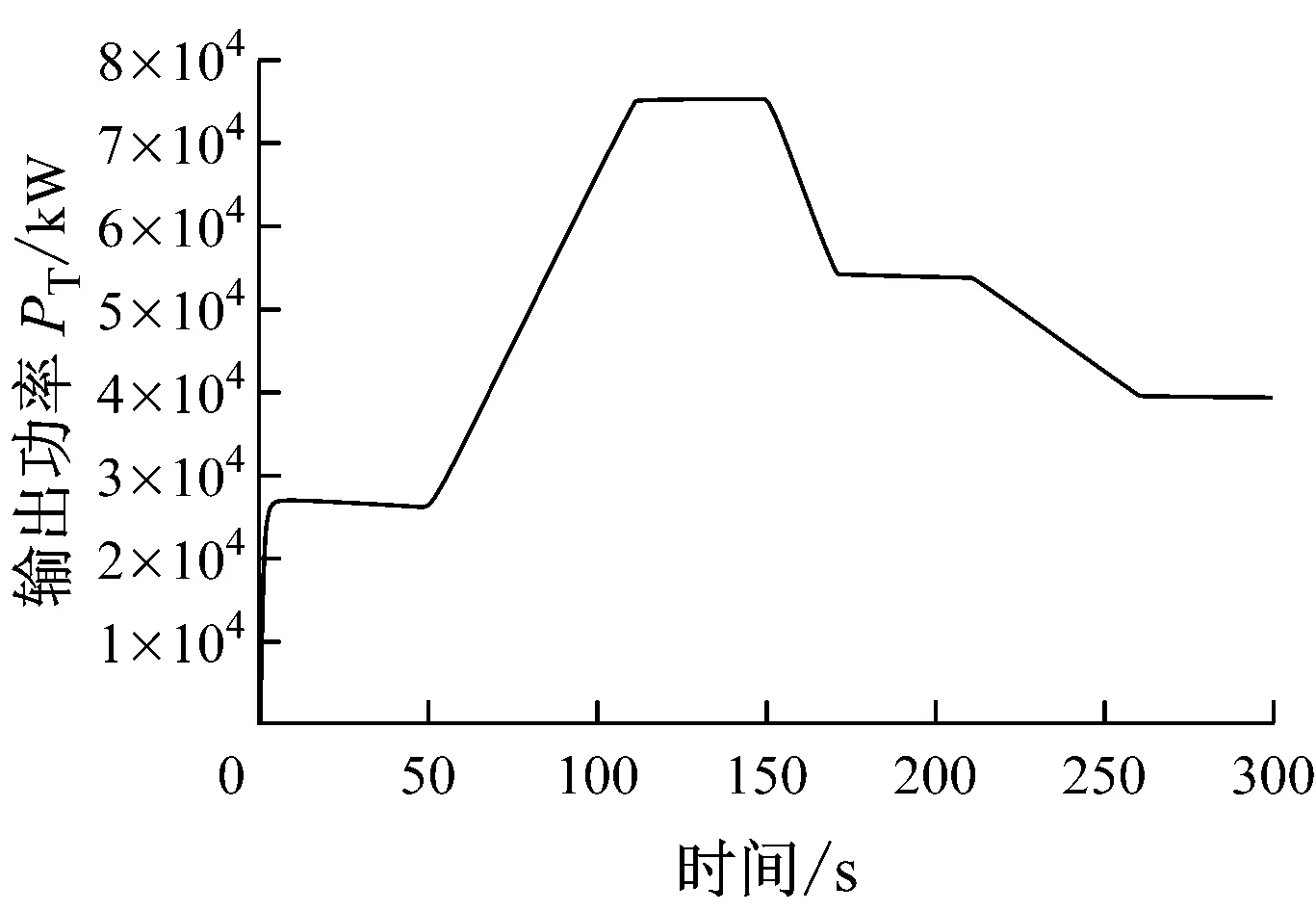
图10　输出功率PT变化曲线

为了进一步验证燃气轮机系统模型，在该系统中，将-0.3%额定转速(即-0.3%nd)加到额定转速下进行测试，如图3所示.相关测试结果如图12和图13所示.由图12和图13可知，加入-0.3%nd的转速扰动(约60 s时)后，温度控制介入并减少燃料量qm,f，从而降低排气温度T4，保护燃气轮机免受高温损害，这与实际情况相符合.

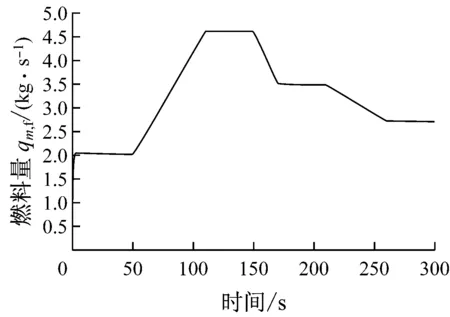
图11　燃料量qm,f变化曲线

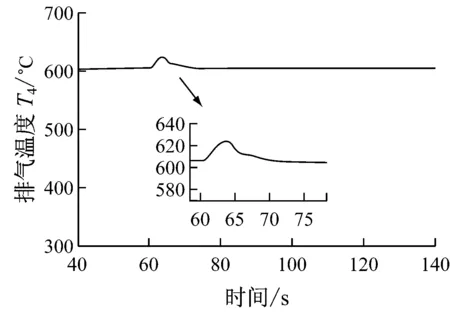
图12　排气温度T4变化曲线(-0.3%nd)

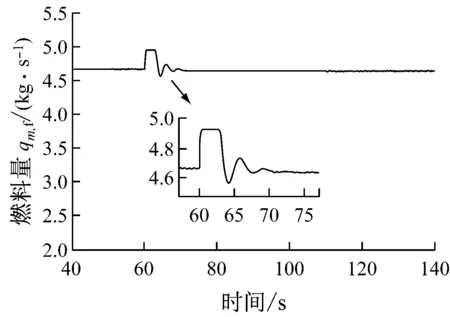
图13　燃料量qm,f变化曲线(-0.3%nd)

5　结　论

基于Rowen模型，建立燃气轮机及其控制系统的数学模型，并利用机组现场运行数据，对模型相关参数进行估计.同时，以GE MS6001FA型燃气轮机为研究对象，给出燃气轮机建模及参数估计的具体方法和过程，并进行了相关仿真实验.仿真结果表明，该模型能够正确再现燃气轮机加、减负荷等工况，且符合燃气轮机实际运行规律，具有一定的研究和参考价值.

[1]蒋洪德. 加速推进重型燃气轮机核心技术研究开发和国产化[J].动力工程学报，2011，31(8)：563-566.

JIANG Hongde. Promote heavy duty gas turbine core technology development and industrial application in China[J]. Journal of Chinese Society of Power Engineering, 2011, 31(8): 563-566.

[2]付云鹏，黄宜坤，张会生，等. 一种考虑变几何特性的重型燃气轮机建模方法[J].动力工程学报，2014，34(3)：200-204.

FU Yunpeng, HUANG Yikun, ZHANG Huisheng,etal. A modeling method for heavy gas turbines considering variable geometry characteristics[J]. Journal of Chinese Society of Power Engineering, 2014, 34(3): 200-204.

[3]韦思亮，刘尚明，倪维斗. 有差调节系统燃气轮机在Matlab/Simulink中的实现[J].动力工程，2001，21(6)：1555-1559.

WEI Siliang, LIU Shangming, NI Weidou. Simulation of gas turbine with droop control system under Matlab/Simulink[J]. Power Engineering, 2001, 21(6): 1555-1559.

[4]魏静，陈艳军，张建国. 联合循环电站燃气轮机控制系统的建模研究[J].燃气轮机技术，2011，24(1)：45-50.

WEI Jing, CHEN Yanjun, ZHANG Jianguo. Research on modeling of gas turbine control system in combined cycle power plant[J]. Gas Turbine Technology, 2011, 24(1):45-50.

[5]邬健，余又红，贺星. 几种典型燃气轮机控制模型的比较和分析[J].燃气轮机技术，2015，28(2)：44-49.

WU Jian, YU Youhong, HE Xing. Comparison and analysis of several typical gas turbine control models[J]. Gas Turbine Technology, 2015, 28(2):44-49.

[6]刘尚明，李忠义. 基于SIMULNK的单轴重型燃气轮机建模与仿真研究[J].燃气轮机技术，2009，22(3)：33-39.

LIU Shangming, LI Zhongyi. Modeling and simulation of single shaft heavy duty gas turbine using SIMULINK[J]. Gas Turbine Technology, 2009, 22(3):33-39.

[7]ROWEN W I. Simplified mathematical representations of heavy-duty gas turbines[J]. ASME Journal of Engineering for Power, 1983, 105: 865-869.

[8]ROWEN W I. Simplified mathematical representations of single shaft gas turbines in mechanical drive service[C]//ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition. Germany: American Society of Mechanical Engineers, 1992.

[9]YEE S K, MILANOVIC J V, HUGHES F M. Overview and comparative analysis of gas turbine models for system stability studies[J]. IEEE Transactions on Power Systems, 2008, 23(1): 108-118.

[10]TAVAKOLI M R B, VAHIDI B, GAWLIK W. An educational guide to extract the parameters of heavy duty gas turbines model in dynamic studies based on operational data [J]. IEEE Transactions on Power Systems, 2009, 24(3): 1366-1374.

A Modeling Method for Heavy Duty Gas Turbines and the Parameters Estimation

HUANGYuzhu,JIANGHongde

(National Research Center of Gas Turbine and IGCC Technology, Tsinghua University,Beijing 100084, China)

To study the dynamic characteristics of a gas turbine, models of the gas turbine and its control system were developed based on Rowen model, while the model parameters were estimated with field data according to the laws of mass, momentum and energy conservation using basic thermodynamic formulas. Taking the GE MS 6001FA gas turbine as an object of study, specific modeling way of the gas turbine was described in detail, including its parameters estimation. Results show that the model developed can effectively reflect the dynamic characteristics conforming to actual operating rules of the gas turbine, which therefore may serve as a reference for study of similar gas turbines.

gas turbine; Rowen model; parameters estimation; field data

2015-06-03

2015-11-30

中国博士后科学基金资助项目(2014M560974)

黄玉柱(1985-)，男，河北石家庄人，博士，主要从事火电机组建模、控制与优化等方面的研究.电话(Tel．)：13401146281；

E-mail：hyzweed@163.com．

1674-7607(2016)08-0600-08

TK47

A学科分类号：470.30