带橡胶球铰的车用推力杆稳定性分析*

卜继玲，　周　炜，　李建林，　黄友剑

(株洲时代新材科技股份有限公司，湖南 株洲 421007)



带橡胶球铰的车用推力杆稳定性分析*

卜继玲*，周炜，李建林，黄友剑

(株洲时代新材科技股份有限公司，湖南 株洲 421007)

车用推力杆在极限承载下会发生忽然弯曲而导致结构失稳破坏，影响车辆运行安全．本文对车用推力杆的稳定性进行了分析，建立了带橡胶球铰的失稳临界载荷数学模型，通过对推力杆屈曲模态的分析，进一步验证了该模型的可行性．由于考虑了球铰弹性支撑的作用，该计算方法更具有指导意义和工程价值．

橡胶球铰；稳定性；失稳临界载荷；推力杆

汽车推力杆应用于双后桥平衡悬架和空气悬架载重车和客车上，用来保持两车桥之间或车桥与车架之间的相对位置，传递汽车的纵向力和横向力[1].推力杆一端连接在车桥上，一端连接在车架上，能缓和抑制由路面不平引起的振动和冲击，对于乘坐的舒适性和所运货物的完好性具有一定的改善作用．在悬架设计时，通过合理布置推力杆，还可提高车辆整体的抗振、抗扭性能，保证车辆具有良好的操纵稳定性．随着空气悬架客车和重载货车的迅猛发展，汽车悬架推力杆得到广泛应用，需求量大幅度增加．

汽车推力杆主要由球头、球铰和套管组成(如图1所示)，在汽车行驶和制动过程中，推力杆主要承受纵向拉伸和压缩两种载荷作用．车用推力杆其本质上属于细长杆结构，主要承受拉伸和压缩载荷，因此在设计上不但要考虑特定的强度、刚度要求，其压杆稳定性也是设计者需要考虑的重要方面．本文对具有弹性支撑压杆的失稳临界载荷进行了研究，建立了基于弹性支撑座的压杆稳定数学模型，并利用仿真分析方法进行了验证．

1　压杆失稳临界载荷

工程结构或构件在荷载作用下处于静力平衡状态，若在任意微小外界扰动下偏离其平衡位置，当外界扰动除去之后如果仍能自动回复到原来位置，则原有平衡是稳定的；如果不能回复到原有平衡位置，则原来的状态是不稳定的．从稳定平衡状态过渡到不稳定平衡状态为临界状态．压杆结构失稳的原因是因杆类结构具有一定的刚度，过度承载会使其结构内部出现负刚度，导致其承载能力下降，当负刚度等于结构本身的刚度时，杆件就失去了承载能力，整个系统出现了失稳现象．由于失稳现象通常是突然发生的，因此工程上压杆的失稳往往会造成严重的后果．

常规的压杆稳定性计算一般都将压杆两端支座简化为固定、固定铰支和活动铰支等几种理想约束，其失稳临界载荷的欧拉公式如下[2]：

(1)

其中：Pcr为临界载荷；E为材料弹性模量；I为横截面最小惯性矩；μ为长度系数,长度系数仅和压杆的固定和铰支约束方式有关系．

对于一般杆件而言，欧拉公式可以完成失稳临界载荷的计算，但是对于车用推力杆，其支座为球头加球铰结构，由于球铰是具有一定的偏扭转刚度的，属于弹性支座范畴，其约束特点介于固定和铰支之间，因此，推力杆的失稳临界载荷也应该是介于这两种约束所对应的临界载荷之间．由推力杆的球头和球铰组成的弹性支座可以简化成铰支座和扭簧的组合约束结构，其简化结构如图2所示.

图2所示组合压杆的绕曲线方程为[3]：

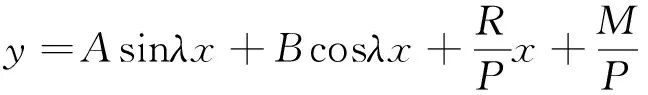
(2)

由于推力杆两端一般采用相同的球铰，即图2所示扭簧的刚度系数相同,均为k，由对称性可知，组合压杆的约束反力R=0.依据组合压杆的边界条件的设定：当x=L/2时，y′(L/2)=0，当x=0时，杆件挠度y=0,M(0)=ky′(0),可以得到如下的线性方程组：

(3)

通过求解，可以得到组合压杆临界载荷的表达式为：

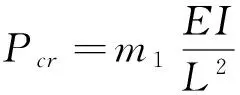
(4)

(5)

由式(5)可知，m1与扭簧的刚度相关，其数值计算结果如表1所示.

针对某型重载货车的平衡悬架用推力杆结构，杆长1 600 mm，截面为圆环状，D=60 mm，d=44 mm，推力杆材料弹性模型E=210 GPa，两端橡胶球铰的扭转刚度为400 N·m/deg，根据推力杆装车情况，牵引杆长度系数取μ=1，根据式(5)可以求出m1的数值解为11.354 8．根据欧拉公式可以求出推力杆失稳临界载荷Pcr1=366.1 kN，根据弹性支座失稳临界载荷公式可以求出Pcr2=421.2 kN，可见通过提高推力杆球铰偏扭转刚度可以提高产品的抗失稳能力．

表1　两端为组合约束压杆系数m1的数值解Tab.1　The arithmetic solution of m1 for the both ends of constraint pressure bar

2　仿真分析验证

屈曲分析是一种用于确定结构开始变得不稳定时的临界载荷和屈曲模态形状(结构发生屈曲响应的特征形状)的技术，屈曲分析可以用于结构的稳定性分析[4]．利用Abaqus软件的屈曲分析功能，本文通过推力杆的稳定性分析，对弹性支撑临界失稳载荷分析的可行性做进一步验证．

在Pro/e软件中建立平衡梁悬架用推力杆几何模型，并导入Abaqus软件．分析过程不考虑金属与橡胶之间的粘结强度，将橡胶与金属作为整体分析，橡胶与金属相连面共节点，并在不影响计算精度的前提下，对模型中的细节进行了几何简化：去掉小圆角、金属表面的附胶薄层等．运用Abaqus中的C3D8R单元和密度较大的C3D4单元模拟金属件、C3D8H模拟球铰的橡胶单元，网格数量在278 242个以上，具体见图3．球头、套管和球铰芯轴的材料分别为45#(正火HB150-210)，Q345C和40Cr．

在初始外力100 kN作用下，通过屈曲分析可以得到推力杆一阶屈曲模态结果，如图4所示，其特征值为4.175，因此推力杆的临界失稳载荷为417.5 kN，如表2所示．

表2　平衡梁失稳临界载荷计算结果Tab.2　Results of the critical load for balance beam

计算得到的临界失稳载荷，对推力杆进行强度校核，套管的最大Mises应力为318.3 MPa，低于材料的屈服强度．从材料强度看满足设计要求，但是由于存在失稳的可能性，因此该平衡梁悬架用推力杆的极限载荷的设计要求应该低于421.2 kN．

由表2可知，仿真分析结果与弹性支撑计算结果基本一致，欧拉公式的计算结果偏于保守，弹性支撑的失稳临界载荷计算方法可以用于指导产品设计．

3　结　论

建立了弹性支撑座压杆的数学模型，通过推力杆屈曲模态分析验证了该模型的可行性.分析结果表明，由于橡胶球铰存在一定的偏扭转刚度要求，单纯用欧拉公式进行失稳临界载荷计算偏于保守，因此考虑弹性支撑座的压杆稳定性分析更具有一般意义和工程价值．

[1]余志生．汽车理论[M]．北京：机械工业出版社，2000.

[2]孙训方,方孝淑,关来泰．材料力学Ⅱ[M].北京：高等教育出版社，2002.

[3]刘协全,倪新华．支座弹性对压杆临界载荷的影响[J].军械工程学学报,2003(15)：73-78.

[4]张晓霞,姚远．基于ANSYS机车牵引杆屈曲分析[J].机械,2008，35(7)：36-37.

责任编辑：罗联

Stability Analysis for Vehicle Torque Rod Based on the Rubber Bushing

BUJi-ling*，ZHOUWei,LIJian-lin，HUANGYou-jian

(Zhuzhou Times Newmaterial Technology Co., Ltd, Zhuzhou 412007 China)

Under the ultimate bearing, suddenly bending occurs to vehicle torque rod, this would lead to structure instability and failure, and influence vehicle safety of operation.The stability of the vehicle torque rod is analyzed in this paper. Based on the rubber bushing, the mathematical model for the instability critical force is derived. Through the buckling modal analysis for the vehicle torque rod, the feasibility of the mathematical model is verified. For considering the elastic support, this method is more significance and engineering value．

rubber bushing；stability；instability critical force；vehicle torque rod

2015-12-10

卜继玲(1974-)，男，湖南 浏阳人，博士，教授级高级工程师. E-mail:jlwujlbu@163.com

U463.33

A

1000-5900(2016)01-0039-03