商用车子午线轮胎滚动噪声仿真研究*

王鹏斌，　项大兵，　周福强，　危银涛，　罗文波*

(1.湘潭大学 土木工程与力学学院,湖南 湘潭 411105；2.清华大学 汽车安全与节能国家重点实验室,北京 100084)



商用车子午线轮胎滚动噪声仿真研究*

王鹏斌1，项大兵2，周福强2，危银涛2，罗文波1*

(1.湘潭大学 土木工程与力学学院,湖南 湘潭 411105；2.清华大学 汽车安全与节能国家重点实验室,北京 100084)

商用车产生的噪声对道路两侧的行人与住宅造成极大的危害．研究轮胎不同部位的噪声分布，对分析轮胎噪声的产生机理与控制车辆行驶噪声有非常重要的意义．本文利用Abaqus和LMS Virtual.Lab软件对商用车子午线轮胎进行动力学和声学仿真,通过混合拉格朗日-欧拉方法(MLE)，将轮胎有限元动力学参量映射到声学有限元网格节点上，最后在自动匹配层技术(AML)基础上进行了轮胎振动噪声的有限元仿真，得到轮胎周围声场的噪声分布云图和频谱曲线．块状花纹载重子午线轮胎的仿真结果与试验结果吻合较好，通过MLE方法可以得出轮胎噪声声源主要位于轮胎接地点前/后部,而不是轮胎接地正中间．

噪声实验；子午线轮胎；有限元；混合拉格朗日-欧拉方法

车辆行驶噪声已成为道路噪声的主要来源之一．有研究表明，当乘用车速度大于60 km/h，商用车速度大于80 km/h时，轮胎噪声超过其他噪声源，成为汽车行驶噪声的主要来源[1～3]．尤其对于商用车，产生的噪声对道路两侧的行人与住宅造成极大的危害．研究轮胎接地区域及附近的噪声分布，探讨轮胎不同角度、不同部位的声辐射强度，对分析轮胎噪声的产生机理与控制车辆行驶噪声有非常重要的意义．

轮胎噪声的产生机理非常复杂，主要包括与空气动力相关的泵浦噪声、空气柱共鸣噪声、赫姆霍兹共振噪声、空气紊流噪声；与振动相关的胎面冲击振动噪声、花纹块粘滑振动噪声和粘吸振动噪声[4，5]．由于轮胎噪声的发声和传播机理非常复杂，很难使用一种普遍的理论或模型对其进行解释和研究，更加缺乏有效的试验手段对其中一种机理进行隔离研究．使用仿真分析的方法分析轮胎噪声，不但可以隔离研究振动噪声或气动噪声，还可以将仿真输出结果与实验进行对比分析[6]．本文主要从轮胎振动机理出发，通过混合拉格朗日-欧拉方法(MLE)，将轮胎有限元动力学参量映射到声学有限元网格节点上，对滚动轮胎振动噪声进行仿真．

1　仿真分析

1.1混合拉格朗日-欧拉方法

轮胎滚动噪声仿真困难的一个主要原因是滚动动力学分析需要在拉格朗日体系下进行，而噪声分析一般在欧拉体系下进行，两种体系之间的信息交换难以进行[7，8]．Abaqus计算所得的轮胎表面节点加速度和位移信息是在随轮胎滚动的拉格朗日网格中，并不能直接作为声学有限元计算的振动边界条件．本文使用MLE方法对加速度进行网格映射，将跟随轮胎滚动的拉格朗日网格上的加速度信息映射到空间固定的欧拉网格上，从而为声学有限元计算提供完整的振动辐射边界条件．

如图1所示，在整体坐标系o-xyz中，拉格朗日单元e由节点1、2、3、4组成，其空间坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4)；点p为欧拉网格上的任意一个节点，其坐标为(xp,yp,zp)；点p'是点p在单元e所在平面内的投影点．o'-uvw是建立在拉格朗日单元所在平面的局部坐标系．

下面以拉格朗日单元的中心o'点为原点，以直线o'1方向为坐标轴u的正方向推导局部坐标系的坐标阵，进而求出坐标变换矩阵．

对于某个欧拉节点p，若已经识别出其所属拉格朗日网格为e，则可对其进行信息映射．如图2所示，节点1、2、3、4、p的坐标分别是(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)、(xp,yp)． 点A、B、C、D分别是四边形单元每条边的中点．点O是线段AC和BD的交点，也是单元的中心点．

以点O为原点，在单元上创建一个插值坐标系o-ζη．以直线OB和OC的方向为插值坐标系的坐标轴方向，则插值坐标系的坐标矩阵I可以表示为：

(1)

则平面内任意节点的插值坐标(ζi,ηi)可以表示为：

(2)

其中I-1是I的逆矩阵．将式(2)代入到插值形函数计算公式(3)中，即可求出单元中所有拉格朗日节点的插值形函数．

(3)

形函数确立以后，拉格朗日网格和欧拉网格中的加速度映射关系可以通过式(4)唯一确定．

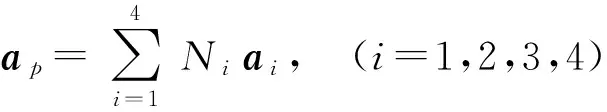
(4)

其中ap是映射到欧拉网格上的振动加速度，ai为映射前的振动加速度信息．

用Fortran语言编写了MLE数据映射程序，实现瞬态滚动的拉格朗日网格上的节点加速度信息向固定的欧拉网格的节点上进行映射，得到欧拉网格节点上随着时间变化的加速度历程数据，从而构建轮胎动力学分析和噪声分析之间的数据桥梁，将轮胎滚动仿真获得的轮胎表面振动加速度时域信号作为声学边界条件，映射到轮胎声学有限元模型上，这是进行轮胎振动噪声仿真的前提．

1.2滚动轮胎动力学仿真

建立三维轮胎有限元模型，对该模型进行动力学分析，得到轮胎滚动时的力学特性，主要包括轮胎模型节点上的位移、速度、加速度等信息．当轮胎在地面上滚动时，胎面连续不断地撞击地面，产生了冲击振动噪声．因此，不同的轮胎花纹结构对轮胎噪声有着很大的影响，胎面花纹的准确建模对轮胎振动噪声仿真是一项非常关键的工作．对于光面轮胎或简单的纵沟轮胎，胎面花纹可以和轮胎的其他部件进行整体建模，然后通过二维模型的旋转来得到一个完整的三维轮胎模型(如图3所示)．然而，大部分轮胎具有比较复杂的花纹结构，其花纹无法通过二维的模型旋转获得．这种情况下，必须单独建立完整的三维轮胎花纹模型，然后装配到轮胎的其余部件上(如图4所示)．为了保证胎面的连续性，将轮胎花纹块和花纹沟建成一个整体，使得花纹块和花纹沟交界处均为共节点单元．这种建模方法不但提高了有限元计算精度，而且使轮胎的花纹沟表面和花纹块表面成为连续的曲面，方便轮胎外表面节点加速度结果的向外输出[9]．

轮胎三维模型建立完成以后，利用Abaqus中的显式有限元算法对轮胎三维模型进行滚动动力学分析，导出轮胎表面节点的振动加速度和位移(空间坐标)信息．通过MLE数据映射程序，完成加速度信息从拉格朗日网格向欧拉网格的映射，为轮胎的冲击振动噪声仿真提供稳定的加速度边界条件[10]．

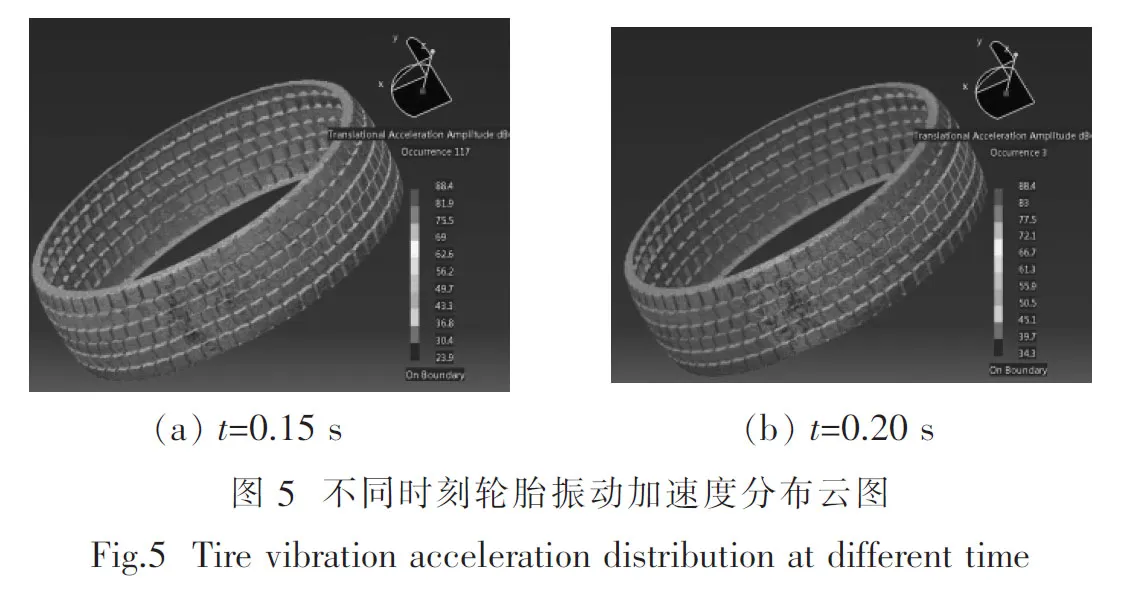
图5给出了某型花纹胎面在不同时刻下的加速度场，图6选取了轮胎接地部位前、中、后三点的加速度数值并进行了对比，从中可以总结出如下几条规律：

(1) 轮胎胎面剧烈振动主要集中在接地区域，其他区域相对较小．

(2) 加速度在接地区域内呈不均匀分布，接地区域中心由于胎面与地面紧密贴合，因此振动加速度较小，而接地区域中心两侧节点振动更加剧烈．

(3) 尽管接地区域前端加速度数值略大于接地后端加速度数值，但是由于接地后端的加速度剧烈区域分布更为广泛，从而导致接地区域后端振动噪声大于前端．

1.3声学仿真

自动匹配层(Automatic Matched Layer)技术是LMS Virtual.Lab团队在声学完美匹配层(Perfect Matched Layer)技术基础之上发展而成的一种新型的声学有限元方法[11～15]．本文在自动匹配层技术(AML)基础上进行了轮胎振动噪声的有限元仿真．

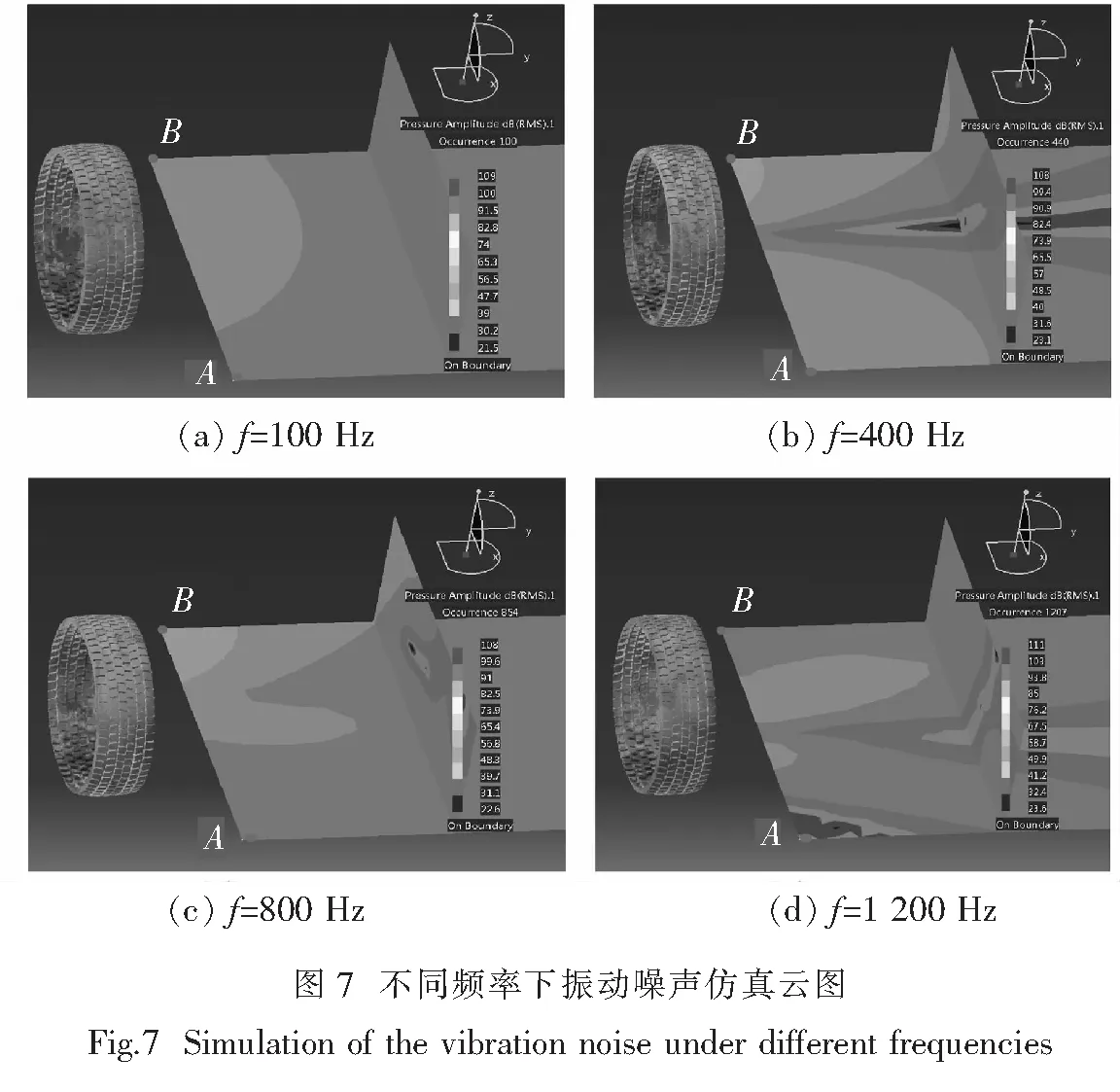
以某品牌块状花纹轮胎为例，图7为该轮胎在不同频率下自由声场中的振动噪声仿真云图．图中的点B位于轮胎接地区域后端，点A位于轮胎接地区域前端．从图7中可以明显看出B点周围的声压要大于A点周围，即接地区域后端声压要高于接地区域前端．

图8给出了场点A和B处的轮胎振动噪声频谱曲线，从中可以明显看出，在大部分频段B点声压级要高于A点．上述结论与试验结果相一致，说明基于MLE方法的轮胎振动噪声仿真能够很好地表现轮胎周围声场强弱的分布情况．

图9是自由声场和半自由声场中的振动噪声仿真以及近场试验结果频谱图[16]．图中的三条频谱曲线取自空间中相同位置的参考点，轮胎噪声仿真时工况和试验时的工况保持一致．

从图9可知：

(1) 基于MLE方法的轮胎振动噪声仿真频谱曲线与轮胎近场噪声试验频谱曲线的趋势和规律较为一致，能够基本反映出该款轮胎噪声的频谱规律．

(2) 半自由声场中的噪声仿真结果要高于自由声场中的噪声仿真结果，而在大部分频段内试验频谱曲线则位于二者之间．这是因为轮胎噪声近场试验时，转鼓和地面对声波既有反射作用又有吸收作用．自由声场中轮胎噪声仿真时忽略了地面的这两种作用，从而仿真结果小于试验结果．而半自由声场中轮胎噪声仿真时只考虑了地面的反射作用忽略了其吸声作用，因此噪声仿真结果要大于试验结果．

2　结　论

通过试验和仿真分析商用车轮胎滚动噪声声场，得出以下结论：

(1) 轮胎噪声声源主要位于轮胎接地点前/后部，而不是接地最中间位置．

(2) 通过混合拉格朗日-欧拉方法，将轮胎有限元动力学参量映射到声学有限元网格节点上，对滚动轮胎冲击振动噪声进行仿真，块状花纹载重子午线轮胎的仿真结果与试验结果吻合较好．

[1]BIERMANN J W. Vehicle Acoustics[M]. Aachen,2012.

[2]张宇, 苏清祖. 车辆噪声与控制[J]. 机械设计与制造工程, 1999, 28(2): 44-45.

[3]SANDBERG U,DESCORNET G. Road surface influence on tire/road noise-1[C]//Proceedings of the International Conference Noise Control Engineering, Noise Control for the 80's, Inter-Noise 80, Vol. 1, Miami, Florida, December 8-10, 1980：259-266.

[4]SANDBERG U,EJSMONT J A. 3 basic methods for measurement of tire-road noise [J].Noise Control Engineering Journal, 1984, 23(3): 98-98.

[5]SANDBERG U,EJSMONT J A. Tyre/road noise reference book[M]. Sweden:INFORMEX,2002.

[6]范俊岩. 轮胎噪声研究的现状与发展[J]. 轮胎工业, 2006, 26(4): 195-197.

[7]张涛, 李兵, 夏源明. FEM/BEM 在轮胎振动和噪声特性分析中的应用[J]. 汽车技术, 2005 (9): 12-15.

[8]包秀图, 张涛, 李子然，等. 轮胎振动噪声的数值模拟[J]. 振动与冲击, 2008, 27(11): 6-11.

[9]石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M].北京：机械工业出版社, 2006.

[10]冯希金, 危银涛, 项大兵，等. 基于MLE方法的滚动轮胎冲击噪声仿真分析[J]. 噪声与振动控制, 2015.

[11]詹福良, 徐俊伟. Virtual. Lab Acoustics 声学仿真计算从入门到精通[M].西安：西北工业大学出版社, 2013.

[12]HU F Q. A stable, perfectly matched layer for linearized Euler equations inunsplit physical variables[J]. Journal of Computational Physics, 2001, 173(2): 455-480.

[13]BÉCACHE E, FAUQUEUX S, JOLY P. Stability of perfectly matched layers, group velocities and anisotropic waves[J]. Journal of Computational Physics, 2003, 188(2): 399-433.

[14]ATASSI O V. Nonreflecting boundary conditions for the time-dependent convective wave equation in a duct[J]. Journal of Computational Physics, 2004, 197(2): 737-758.

[15]HU F Q. Development of PML absorbing boundary conditions for computational aeroacoustics: A progress review[J]. Computers & Fluids, 2008, 37(4): 336-348.

[16]陈亚龙.C3轮胎通过噪声的室内外对比研究[D].北京：清华大学,2014.

责任编辑：罗联

Simulation of Rolling Noise of Truck Tires

WANGPeng-bin1,XIANGDa-bing2,ZHOUFu-qiang2,WEIYin-tao2,LUOWen-bo1*

(1.College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105;2.State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084 China)

The rolling noise caused by truck tires is harmful for residential on either side of the road and people. It is very important to study tire noise in different frequency distribution, by which we can analyze the mechanism of tire noise and control vehicle noise. This paper extends Mixed Lagrange-Euler (MLE) method to simulate the vibration noise of the rolling tire, taking truck and bus radial tires (TBR) as the main research objects, using Abaqus and LMS Virtual Lab software. By Mixed MLE method, finite element mechanics parameters are mapped to acoustic finite element grid node. A series methods and procedures to simulate the tire vibration noise based on the Automatic Matched Layer technology are researched. And the noise distribution graph and frequency spectrum around the tire are calculated. The simulation results are in good agreement with experiment results for block pattern tire, and the tire noise source is located mainly in front/rear site of tire grounding part, not the middle of tire grounding part.

noise experiment;radial tire; finite element;Mixed Lagrange-Euler method (MLE)

2015-12-10

国家自然科学基金项目(51275265，11572275)

罗文波(1969-)，男，湖南 湘乡人，博士，教授，博士生导师. E-mail:luowenbo@xtu.deu.cn

U463.341

A

1000-5900(2016)01-0033-06