再制造最优生产计划模型的CVaR凸逼近及SAA算法*
2016-08-26杨柳,向琼,熊瑶,彭伶
杨 柳, 向 琼, 熊 瑶, 彭 伶
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
再制造最优生产计划模型的CVaR凸逼近及SAA算法*
杨柳*,向琼,熊瑶,彭伶
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
研究企业再制造综合生产计划问题,构建了一个更符合实际的带联合概率约束的最优化模型.针对此非凸优化问题求解上的困难,采用CVaR逼近将模型等价转化为凸优化模型,然后运用样本平均近似方法进行求解,证明了算法的收敛性,数值结果表明了模型和算法的有效性.
再制造综合生产计划;联合概率约束;CVaR;样本平均近似
本文主要研究市场需求量和废旧产品回收量不确定的情况下,再制造综合生产计划模型的建立及求解.首先针对问题的特点建立联合概率约束模型,用CVaR凸内逼近方法作等价转化,再用样本平均值近似(SAA)算法实现数值求解.模型具有以下优点:(1)在未来的生产计划中用联合概率约束来表示产品库存的最低要求;(2)针对概率约束随机问题,引入CVaR逼近方法将模型转化为能快速求解的凸逼近优化问题;(3)设计样本平均近似方法求解转化后的CVaR模型,证明在大样本条件下,近似模型的最优解依概率1收敛于原模型的最优解.
1 基于联合概率约束的再制造综合生产计划模型
本文考虑单一产品,生产计划期为N.每期的产品市场需求量ζi(i=1,…,N.)已通过预测得到.如果需求在当期不能被满足,则订单延迟至下一期,即不考虑缺货成本.废旧产品回收量yi是满足一定分布的随机变量.第i期对废旧产品进行处理的单位成本为ri,包括拆卸、翻新等处理后达到新产品的标准.第i期生产单位新产品的成本为λi,新产品的产量为xi,单位产品库存成本为hi,第i期库存量为gi(xi,yi).
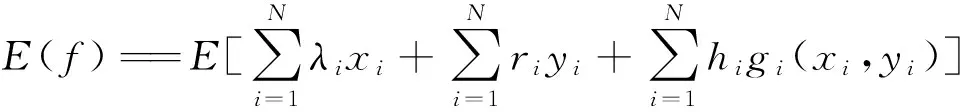
其中,第一项为企业的再制造成本;第二项为企业回收废旧产品成本;第三项为企业的库存成本.由于目标函数中只有废品回收量yi是一个随机变量,故目标函数可表示为:
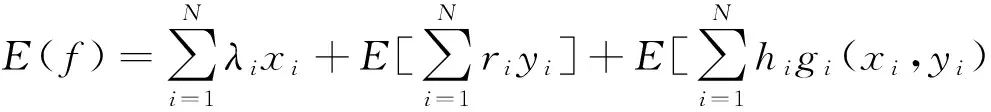
再制造企业产品应满足产品库存平衡约束:
gi(xi,yi)=gi-1+xi+yi-ζi,
(1)
假定各计划期产品库存量小于零的概率低于某一事先给定的置信水平αi,则应满足产品库存概率约束:
P{gi(xi,yi)<0}≤αi.
(2)
如果需求在当期不能被满足,则订单延迟至下一期,即不考虑缺货成本,因而新产品产量应满足非负约束,即xi≥0.因此,可构建再制造企业综合生产计划的模型如下:
(3)
模型(3)中满足库存的最低要求是一个概率约束,因此本模型可视为一个联合概率约束模型[1,3].该模型由Charnes和Cooper提出[4],这类随机规划问题往往很难求出确切的解析解,而只能从实际出发求出该模型的满意解或次优解.
2 再制造综合生产计划模型的CVaR凸内逼近
假设初期库存量为0,由(1)迭代求出第i期的库存量为:
晚饭后,许灵均拿出来身边仅有的一点钱,给了女孩。告诉她,用这个做路费,回家去吧。他觉得不能乘人之危。女孩难过地说:“你嫌我丑?”当然不是。女孩是真心愿意跟他的:“大家都说我命好。我遇见好人了。”
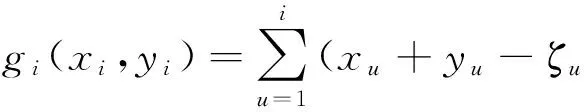
(4)
模型(3)求解的主要困难在于可行域的非凸性,克服此困难的常规做法是用一个易解的凸内逼近来替代难解的联合概率约束.下面我们来构造(3)中概率约束的凸内逼近.易见(2)等价于约束P{-gi(xi,yi)>0}≤αi.令α1=…=αi=…αN=α,则
P{-gi(xi,yi)>0}≤α.
(5)
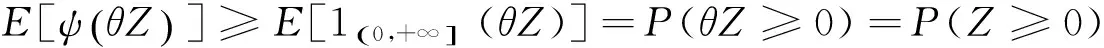
其中,指示函数1A(x)表示当x∈A时为1,当x∉A时为0.令Z=-gi(xi,yi),用θ-1替换θ,由上式得到P{-gi(xi,yi)>0}≤E[ψ(-θ-1gi(xi,yi))],∀θ>0.定义Ψ(xi,θ):=θE[ψ(-θ-1gi(xi,yi))].若∃θ>0满足Ψ(xi,θ)≤θα,则(5)显然成立.我们有[2]

(6)


(7)
由于用θ∈R替换上式中的θ>0是等价的[3],则(7)可等价转化为:

(8)
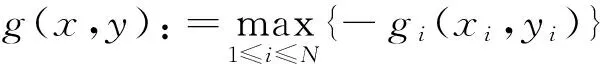
定理1若定义随机函数g(x,y)的风险值(VaR)为:

那么基于VaR上的条件风险值(CVaR)为:

证明若随机函数的VaR值如上,则由基于VaR上的条件风险值CVaR为[11]
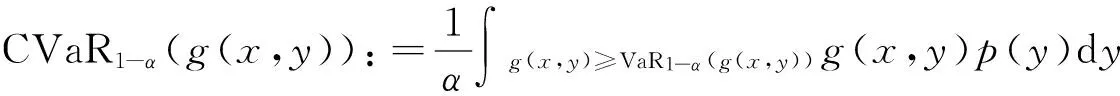
其中,p(y)为随机变量y的密度函数.定义函数:

(9)

CVaR1-α(g(x,y))≤0.
(10)
因此模型(3)可转化为如下CVaR逼近问题:
(11)
3 近似模型的样本平均近似算法及收敛性分析
样本平均近似(SAA)算法的主要思路是用一个随机样本的经验分布来替代概率约束中的真实分布,将问题转化为确定性规划问题后再对其求解.这种方法在带期望值目标函数的随机规划问题的求解中应用广泛,Luedtke和Ahmed研究SAA方法求解概率约束优化问题,详细给出近似问题与原问题解之间的关系[7].接下来我们用SAA算法对模型(11)进行转化.
若g(x,y)是凸函数,则模型中的约束不等式也是凸的[8].易证(10)等价于[13]:

(12)
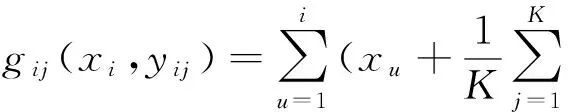
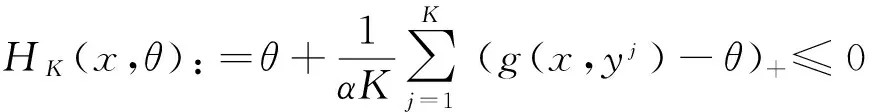
(13)
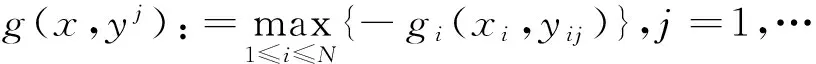
(14)
模型(14)是一个确定性的凸规划问题,可通过Monte-Carlo模拟生成随机变量的样本后调用函数quantile求出VaR值,即参数θ,再调用求解器linprog即可求得此问题的最优解.下面我们来讨论模型(14)的最优解的收敛性.
定理2设SAA问题模型(14)的最优解为X*,则X*以概率1收敛于原问题模型(11)的最优解.

4 数值算例
该问题来自于[3].设某企业再制造工厂综合生产计划的计划周期N=4,各期生产成本λi、废旧产品处理成本ri、库存成本hi相等,具体数据为λi=600元,ri=350元,hi=50元,其中i=1,…,N.各期产品市场需求量可通过对历史数据进行分析预测得到,ζi分别为2 100,2 200,2 500,1 800.各期废品回收量yij满足相互独立的正态分布,均值和方差分别为(660,450).置信度α=0.05.我们得到此问题的概率约束模型如下:
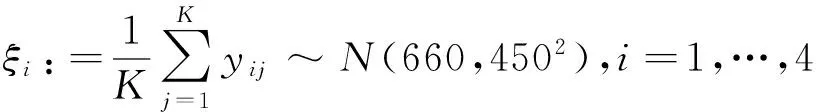
针对上述概率约束模型的求解,我们先对其进行CVaR逼近,然后在此基础上运用SAA算法进行模型转化后用MTLAB求解.通过设置不同样本大小K,数值结果如表1所示.

表1 SAA问题模型的数值结果Tab.1 Numerical results for the SAA model
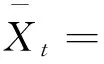
5 结 语
本文针对再制造过程的特点,构建了单一产品再制造企业综合生产计划的联合概率约束规划模型,利用凸内逼近、CVaR逼近的方法对模型进行转化,再运用样本平均近似方法求解,分析了算法的收敛性,最后针对一个具体实例进行了数值实验,验证模型和算法的有效性.本文的结论对再制造综合生产计划的制订具有指导作用和重要价值,后续研究可在模型中考虑缺货成本、增加产品的种类及增加不确定性因素,使模型更加贴近实际,为再制造综合生产计划的制订提供理论支撑.
[1]刘超.再制造企业生产计划建模与优化[D].哈尔滨:东北林业大学,2011.
[2]NEMIROVSKI A,SHAPIRO A.Convex approximations of chance constrained programs[J].SIAM Journal on Optimization,2006,17:969-996.
[3]赵忠.基于确定性近似方法的再制造生产计划[J].工业技术经济,2010(7):93-96.
[4]CHARNES A,COOPER W W.Chance-constrained programming[J].Management Science,1959,6(1):73-79.
[5]CHEN W,SIM M,SUN J,et al.From CVaR to uncertainty set:Implications in joint chance-constrained optimization[J].Operations Research,2010,58(2):470-485.
[6]ROCKAFELLAR R T,URYASEV S.Optimization of conditional value-at-Risk[J].Journal of Risk,2000,2:21-42.
[7]LUEDTKE J,AHMED S.A sample approximation approach for optimization with probabilistic constraints [J]. SIAM Journal on Optimization,2008,19(2): 674-699.
[8] DENG C L,YANG L.Sample average approximation method for chance constrained stochastic program-ming in transportation model of emergency management[J]. Int J Simulation and Process Modeling,2014, 9(4):222-227.
[9]WANG W.Sample average approximation of risk-averse stochastic programs[D].Georgia Institute of Techno-logy,2007.
责任编辑:龙顺潮
The CVaR Convex Approximation and SAA Method for Optimal Re-manufacturing Production Planning
YANGLiu*,XIANGQiong,XIONGYao,PENGLing
(School of Mathematics and Computing Science,Xiangtan University,Xiangtan 411105 China)
This paper is mainly considering the problem of optimal integrated production planning of the re-manufacture. We construct a joint probability constrained optimization model for this problem. As for the difficulty of the non-convex in numerical methods, we first convert the model into a convex optimization problem by using a CVaR approximation equivalently. Then a sample average approximation (SAA) method is used to solve the convex approximated model. We prove the convergence of the SAA method and numerical results are given to show the effectiveness of the model and method.
re-manufacturing integrated production planning; joint probability constraints; CVaR;sample average approximation
2015-11-20
国家自然科学青年基金项目(11301445);湖南省科技厅人才计划项目(2015RS4029);湖南省普通高校教改项目;湘潭大学教改项目(0929/2904036)
杨柳(1975-),女,湖南 益阳人,博士,副教授. E-mail:yangl410@xtu.edu.cn
O224;F830
A
1000-5900(2016)01-0001-05
