重箱转载机械臂的运动学求解与分析

2016-08-26范四立郑永锋舒雨锋丁度坤FANSiliZHENGYongfengSHUYufengDINGDukun东莞职业技术学院机电工程系东莞53808华中科技大学机械科学与工程学院武汉430074

制造业自动化 2016年6期

范四立，郑永锋，舒雨锋，，丁度坤FAN Si-li，　ZHENG Yong-feng，　SHU Yu-feng，，　DING Du-kun（.东莞职业技术学院机电工程系，东莞 53808；.华中科技大学机械科学与工程学院，武汉 430074）

计算机算法

重箱转载机械臂的运动学求解与分析

范四立1，郑永锋2，舒雨锋1，2，丁度坤1
FAN Si-li1，ZHENG Yong-feng2，SHU Yu-feng1，2，DING Du-kun1
（1.东莞职业技术学院机电工程系，东莞 523808；2.华中科技大学机械科学与工程学院，武汉 430074）

以QY-7t型重箱转载机械臂为研究对象，绘制了其三维结构图，阐释了各关节的运动特点，基于标准的D-H参数建模法确定了各关节坐标系及参数表，详细推导了机械臂的正、逆运动学方程，针对反变换法求逆的多解问题，利用神经网络对非线性函数的强大逼近能力，列示了基于遗传算法的RBF神经网络逆解计算框图及其流程图，在MATLAB环境下进行了仿真，结果表明该法求机械臂运动学逆解是可行的，收敛速度及求解精度都能满足机械臂运动控制的要求。

机械臂；D-H模型；运动学正解；逆解；神经网络

0　引言

机器人作为制造领域的高端体现，集精密化、柔性化、智能化、软件应用开发等先进技术于一身，主要由本体结构、控制器、示教系统和监测传感器等组成，特别适应于大载荷、高精度及危险作业环境等极端工况［1，2］。

柔性绳索起吊重物必然会带来摇摆、晃动等诸多不稳定性，要实现转载机构起吊、转运作业的自动化、智能化，采用刚性吊具机构及先进的控制技术是必须的。运动学是工业机器人控制及轨迹规划的基础［3］，本文以某公司生产的QY-7t型随车起重机械臂为研究对象，基于标准的D-H建模方法，对其进行了运动学求解与分析。

1　机械臂结构描述与D-H参数建模

1.1机械臂结构描述

如图1所示，QY-7t型随车起重机械臂结构主要包括回转支撑、底座、折臂、伸缩臂、回转式吊具、油缸及其附件等。其中，底座、折臂、伸缩臂及吊具部分均为由高强钢板焊接围成的箱型结构，具有高强度、重量轻等优点，伸缩臂截面为六边形，臂体共4节，3节顺序伸缩段均通过外置油缸（图1未绘出）进行驱动，机械臂的俯仰、折叠、伸缩及回转等动作均通过液压系统实现。

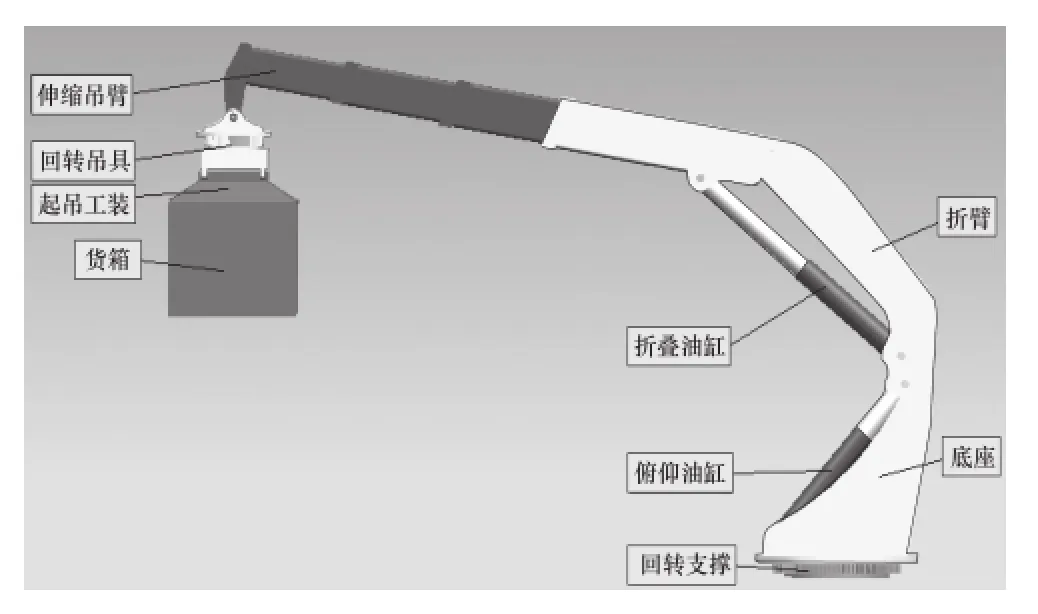
图1　重箱转载机械臂三维结构

1.2D-H参数建模

该型机械臂具有六个自由度，含整体回转、俯仰、折叠、伸缩、吊具前后摇摆及回转功能。基于标准的D-H参数法所确定的各关节坐标系如图2所示。

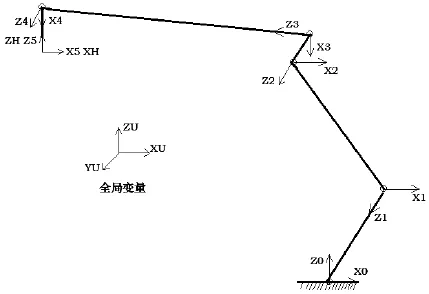
图2　机械臂位姿变换坐标系布局

QY-7t型机械臂的D-H参数如表1所示，其中，各参数释义如下［4］：

θ为绕z轴的旋转角；

d为在z轴上两条相邻的公垂线之间的距离（或称关节偏移）；

a为两个相邻的z轴之间的公垂线的长度（连杆长度）；

α为两个相邻的z轴之间的角度（或称扭角）。

表1　QY-7t型机械臂的D-H参数

2　运动学方程求解

运动学旨在讨论机械臂各关节变量与吊具夹手中心位置之间的关系，可分为两类：正运动学求解与逆运动学求解［5］，机器人正逆运动学关系如图3所示。

2.1正运动学求解

确定了空间坐标系与D-H参数后，由已知关节的关节变量求出机械臂吊具夹手中心相对于基座标系的位姿状态，实现关节空间到笛卡尔坐标空间坐标的转换过程，即为运动学正解。

相邻各杆件之间的变换矩阵如下：

将表1中的参数代入公式（1）中，可得相邻关节的变换矩阵Ai，A1描述了第一关节相对于基座标系的位姿变换，A2描述了第二关节相对于第一关节的位姿变换，以此类推。

式（2）中：

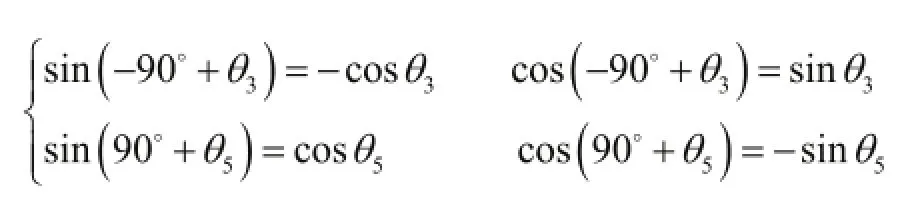
机械臂末端夹手中心相对于基坐标系的变换可表示为：

式（3）中：

2.2逆运动学求解

机器人运动学逆问题在机器人控制中占有非常重要的地位，因为其直接关系到机械臂的离线编程、轨迹规划和实时控制等后续工作，有了运动学逆解才能确定每个关节变量（对于旋转关节，即为求解角度；对于滑动关节，即为求解线性位移），即机械臂达到期望的位姿状态时，能够求得各关节变量值。

由于机器人运动学方程是一组非线性方程，要建立起通用算法是非常困难的。机器人运动学逆分析的方法可分为代数法、几何法和数值法。对于6自由度机械臂，在如下两种情况下其运动学逆解才存在封闭解（Pieper 准则）［6］：

1）相邻3个关节轴交于一点；

2）相邻3个关节轴相互平行。

QY-7t型机械臂第四、五、六关节轴交于一点，满足Piper准则，因而存在封闭的数值解。

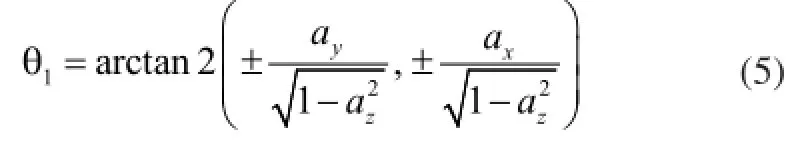
其中，arctan2函数是四象限反正切函数。

2）求θ6变量：

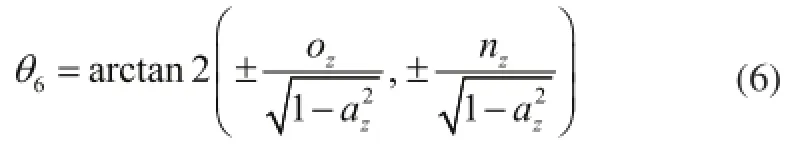
令式（8）两边同时平方，然后相加得：

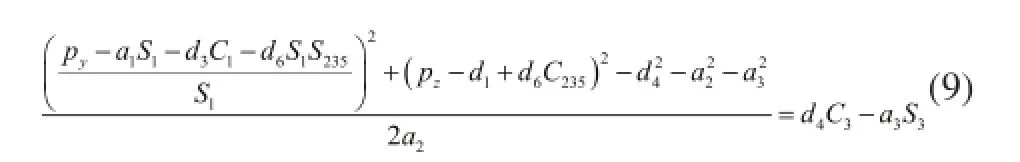
由式（9）不难看出，等式左边均为已知项，未知数均在等号右边，令等式左边等于k1，则式（9）变为：

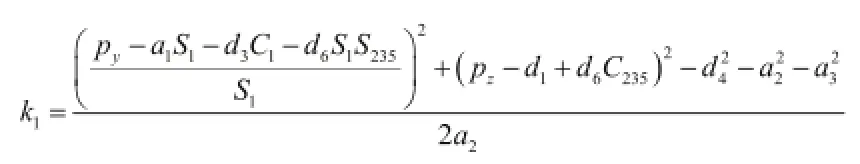
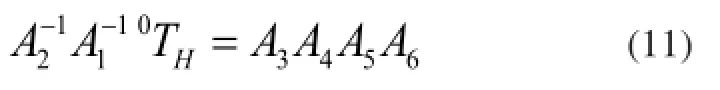
将式（2）中的k2、A2矩阵求逆，代入式（12）中，求得新的矩阵等式，令等式两边的（1，4）元素与（2，4）元素分别相等，整理得：

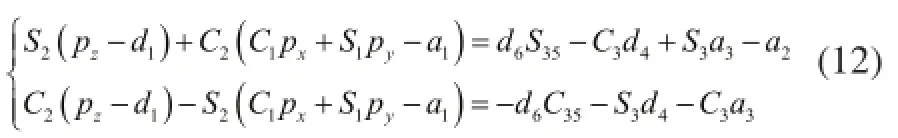
式（12）两边同时平方相加，整理可得：

式（13）中，等式左边及右边关于θ5的系数项均为已知，令等式左边等于k2，则式（13）变为：

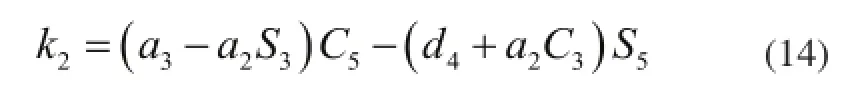
可以看到，式（14）与式（10）具有相同的形式，可参照其计算结果直接求解，易得：

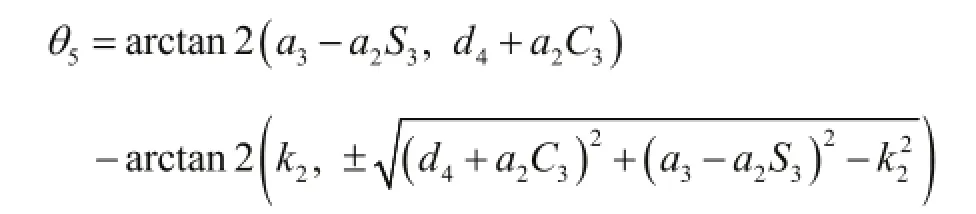
其中：

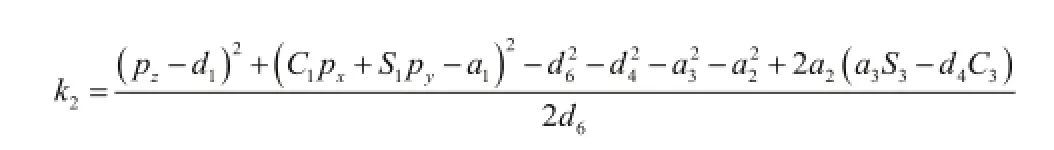
6）求θ2变量：

据以上求解结果可知，机械臂的运动学逆解有若干组，为了在满足求解精度的条件下提高运动控制的收敛速度，须结合机械臂的实际工况与“最短行程准则”，选取合适的方法快速地遴选出一组最优逆解。

3　基于GA的RBF神经网络的求逆

QY-7t型重箱转载机械臂作为一个非线性、强耦合、多变量的复杂系统，神经网络对于非线性系统具有强大的逼近能力，由此将其应用于机械臂运动学逆解求解［7，8］。

神经网络应用比较广泛的是BP算法和RBF神经网络，鉴于BP神经网络的学习速度慢，易陷于局部极值，无法得到全局最优解等问题，本文采用局部逼近网络—径向基函数（Radial Basis Function，简称RBF）网络求解机械臂的逆运动学，其神经元模型如图4所示。

图4　具有R维输入的RBF神经元模型

对于RBP神经网络，其连接权值的选择将直接影响到期望输出与实际输出的误差大小及网络的收敛速度。GA具有良好的全局优化性能和很强的宏观搜索能力，将GA与RBF神经网络相结合，快速选取径向基函数的中心值，方便地得到全局最优解，避免陷入局部极小问题［9］，具体操作流程如图5所示。

图5　基于GA的RBF神经网络逆解计算框图

GA选取隐含层中心值主要是通过自身的交叉概率及变异概率的操作将RBF神经网络的中心值进行不断修正，直至得到最优值。多次迭代后使得RBF的网络适应度函数达到理想设定值，此时的状态对应一个种群个体，将此个体解码，即可找出初始连接权值。得到初始连接权值后，快速的寻找出RBP网络的最佳连接权值，从而输出最优解［10］，基于GA的RBP神经网络求机械臂逆解的流程图如图6所示。

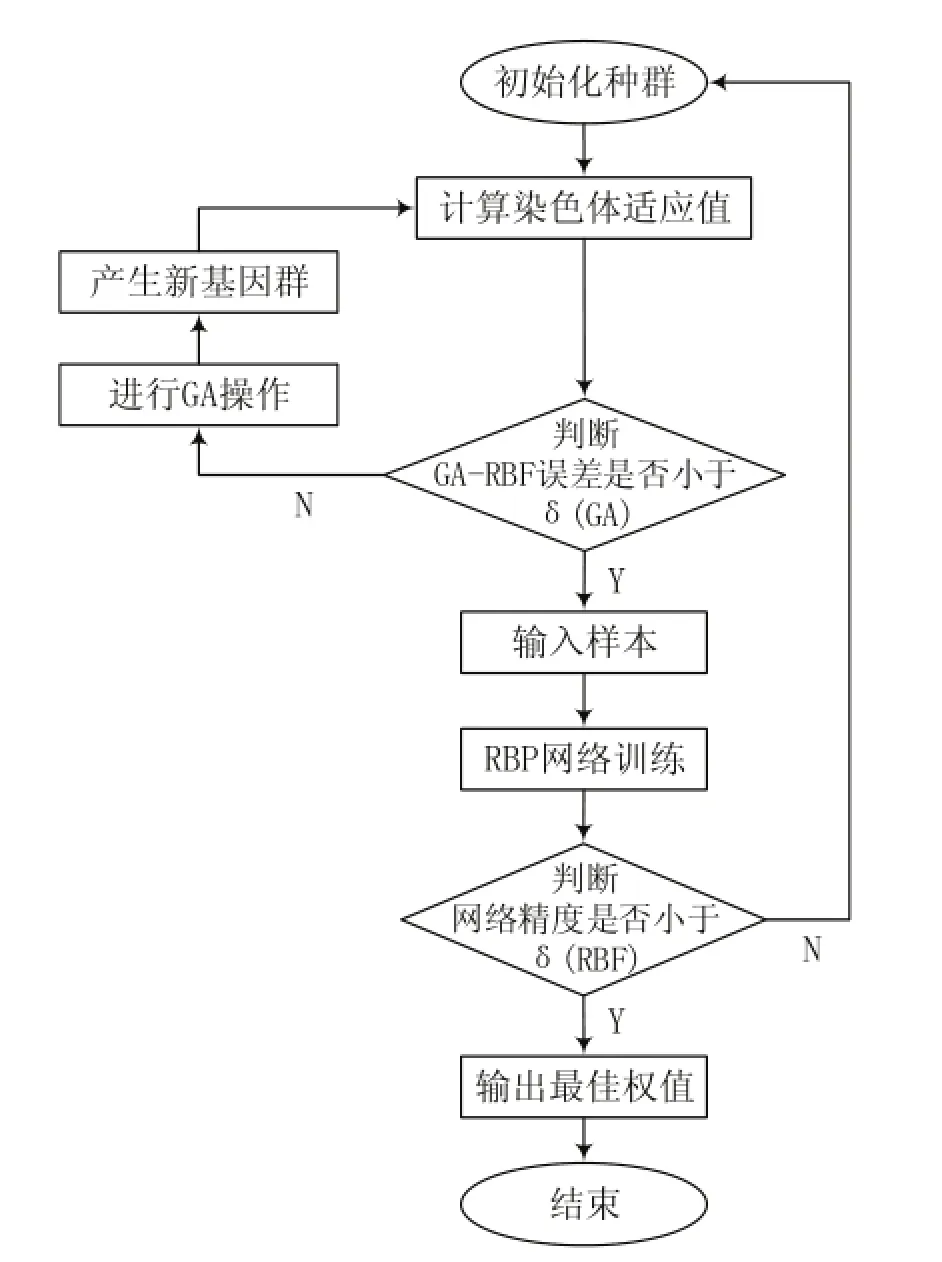
图6　基于GA的RBF神经网络机械臂运动学逆解流程

采用GA学习与θ2，θ3对应的两个RBF网络。初始种群数量定为120，染色体长度l=200，交叉率p1=0.65，变异率pm=0.02，迭代次数设为1200，取2500组输入输出样本进行网络训练。达到稳定状态后，将8组待测样本分别送入两个稳定的网络进行计算。仿真结果如表2所示，两个关节角的期望输出与计算输出的对比曲线如图7，图8所示。

表2中的x，y，z分别代表机械臂末端夹手中心在X方向、Y方向及Z方向的位移。

表2　基于GA的RBF神经网络测试结果

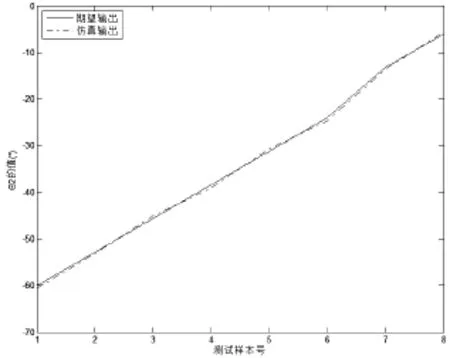
图7　θ2期望输出与仿真输出对比曲线

由以上图表可知，机械臂关节变量的仿真输出与期望输出具有良好地逼近效果，训练稳定的RBF网络求解机械臂的逆运动学是可行的，且收敛速度快，泛化能力强，能够满足机械臂运动学逆解的控制要求。

4　结论

本文分析了QY-7t型重箱转载机械臂的结构特点与运动特性，基于机器人标准的D-H建模方法，详尽地推导了该型机械臂的正逆运动学方程，针对反变化法求逆的多解性，采用基于GA的RBF神经网络法来计算机械臂的逆运动学，并在MATLAB环境下进行了仿真，结果表明该法求机械臂运动学逆解是可行的，收敛速度及求解精度都能满足机械臂运动控制的要求，为该型机构的作业空间包络、控制误差分析及轨迹规划等方面的后续研究奠定了基础。

［1］周建兴，岂兴明，矫津毅，等.Matlab从入门到精通［M］.北京:人民邮电出版社，2012:115-129.

［2］蔡自兴.机器人学［M］.北京:清华大学出版社，2009:20-35.

［3］杨国良.工业机器人动力学仿真及有限元分析［D］.武汉:华中科技大学，2007:17-19.

［4］陈雪华，梁锡昌.基于模块化关节的机器人结构设计和运动学分析［J］.现代制造工程，2005，（2）:8-11.

［5］张普行，严军辉，贾秋玲.六自由度机械手的运动学分析［J］.制造业自动化，2011，33（20）:68-70.

［6］王晓强，王帅军，刘建亭.基于MATLAB的IRB2400工业机器人运动学分析［J］.机床与液压，2014，42（3）:54-58.

［7］孙富春，朱纪洪，刘国栋，等译.机器人学导论-分析、控制及应用［M］.北京:电子工业出版社，2013:25-35.

［8］谢涛，黄鸿.按摩机器人的结构设计及运动学仿真［J］.现代制造工程，2007，（7）:105-107.

［9］王海鸣.基于神经网络的机器人逆运动学求解［D］.合肥:中国科学技术大学，2008:62-69.

［10］胡传俊.神经网络在机械手逆解求解中的应用［D］.湘潭:湘潭大学，2011:42-52.

Kinematics solving and analysis of heavy container transport manipulator

TH212