区域GPS高程拟合方法及实验对比分析

张丕亚,牛冲

(1.山东科技大学 测绘科学与工程学院,青岛 266590;2.山东省地质测绘院,济南 250001)



区域GPS高程拟合方法及实验对比分析

张丕亚1,牛冲2

(1.山东科技大学 测绘科学与工程学院,青岛 266590;2.山东省地质测绘院,济南 250001)

在GPS测量应用中,无法直接利用GPS大地高替代正常高,必须通过高程拟合进行转换。因此,如何利用GPS高程拟合求得正常高成为测绘应用领域研究的一个重要方向。本文在论述常用GPS高程拟合理论模型基础上,通过实例比较分析了几种模型的适用性及可靠性,最后得出一些有益的结论。

GPS;高程拟合;常数拟合法;曲线拟合法;曲面拟合法

0　引　言

相较于传统大地测量,GPS测量有着速度快、精度高、操作简单等特点,已经越来越广泛地应用于实际测绘工作中[1]。但GPS测量采用的高程系统是大地高系统,即以参考椭球面为基准面,而我国目前采用的高程系统是正常高系统,即以似大地水准面为基准面, 若能求出两个水准面之间的差异,即高程异常,就可以将GPS大地高转换成正常高。

参考椭球面是一个理想化的规则球面,但是似大地水准面由于受到重力的影响,是一个不规则的曲面,所以每点的高程异常值不同,因此精确求得高程异常成为GPS高程转换的一个关键因素。在较大区域内精确确定一点的高程异常比较复杂,通常需要结合重力资料、地形资料等,采用物理大地测量的理论方法解算求得高精度大地水准面,但是由于重力资料难以获得,所以在实际工作中难以实施[2]。当测区范围相对不大、地形起伏较小时,各方面影响因素较为接近,高程异常有一定的几何相关性[3]。根据这个原理,可以建立相应的函数模型,进而拟合求得高程异常。GPS高程拟合的方法很多,如常数拟合法、多项式曲线拟合法、样条曲线拟合法、Akima曲线拟合法、多项式曲面拟合法、多面函数拟合法、移动曲面拟合法、神经网络法等[4-5]。本文在介绍常数拟合法、曲线拟合法、垂直平移法、曲面拟合法和多面函数拟合法等的基本原理基础上,通过算例比较各方法的适用性和可靠性。

1　高程拟合的几种方法

1.1常数拟合法

常数拟合法也称加权平均拟合法,其基本原理是根据待拟合点周围的若干已知点进行加权平均,求得高程异常。若测区有n个已知点,其高程异常值为ξi(i=1,2,…,n),则待拟合点的高程异常为

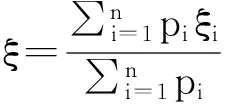
(1)

式中: pi=1/(Di+ε)n(n=1,2,…)为周围已知点高程异常对待拟合点高程异常影响的权重; Di为差值点到已知点的距离; ε一般取0.01.

1.2曲线拟合模型

当GPS点成线状分布时,可以通过数值拟合的方法根据已知点的平面坐标和高程异常构造插值函数,拟合测线方向上的似大地水准面曲线,然后据此内插求得待拟合点的高程异常,进而求出点的正常高[6]。

通常取一个m次的多项式作为插值函数来表示高程异常

(2)

各点的已知高程异常与拟合值残差为

Ri=ξi(xi)-ξi.

(3)

令: L=[ξ1ξ2…ξn]T,β=[a1,a2,…,an]T,

β=(BTB)-1BTL.

(4)

1.3曲面拟合模型

曲面拟合法是最常用的方法之一,其基本思想是:当GPS点成面状分布时,可以认为高程异常在一定范围内变化平缓,根据已知点的平面坐标和高程异常拟合出测区似大地水准面,然后通过内插求得其它点的高程异常,进而求得正常高[7]。

1) 垂直平移法

垂直平移法是最简单的高程转换方法,基本原理是利用若干个已知点的平均高程异常获得其它点的高程异常,进而推求正常高,其公式为

(5)

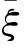
2) 多项式曲面拟合法

当GPS测点成面状区域分布时,常用的拟合方法是多项式曲面拟合法,包括二次曲面拟合法、三次曲面拟合法等。其中用的比较多的是二次曲面拟合法,其公式为

ξ(x,y)=a0+a1x+a2y+a3x2+

a4y2+a5xy.

(6)

总误差方程式为

V=BX-L,

(7)

式中: V=[v1v2…vn]T;

X=[a0a1a2a3a4a5]T;

L=[ξ1ξ2…ξn]T;

根据最小二乘原理,可以求得其待定系数,即:

X=(BTB)-1BTL.

(8)

3) 多面函数拟合法

多面函数拟合法的基本原理是:任何数学表面和任何不规则的圆滑表面,总可以利用一系列规则的数学表面的总和以任意精度逼近[8]。即在每个待拟合点上同所有的已知点建立函数关系,并将这些多面函数的值叠加起来,以获得最佳的曲面拟合值。高程异常函数表达式为

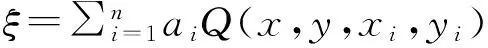
(9)

式中:ai为待定系数;Q(x,y,xi,yi)为核函数;x、y和xi、yt分别为待拟合点和已知点的坐标。核函数有多种形式,通常选取二次函数Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+δ]1/2,δ选取0.01.

令:

L=[ξ1ξ2…ξm]T,

X=[a1a2…an]T,

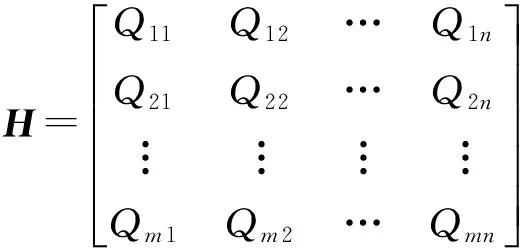
则根据最小二乘原理得

X=(BTB)-1BTL.

(10)

2　算例分析

2.1实验数据

现有某区域无粗差且同精度的GPS/水准点17个(数据选自文献[9]),其大地高、正常高、高程异常如表1所示。

表1　已知点的大地高、正常高和高程异常

2.2拟合结果

为对比分析,将1、2、3、4、5、6、7、8、9、10十个点作为已知点进行拟合,将11、12、13、14、15、16、17七个点作为检核点进行检核。通过MATLAB程序,分别采用常数拟合法、二次曲线拟合法、垂直平移法、二次曲面拟合法、多面函数法进行拟合,各模型拟合结果如表2、表3所示。

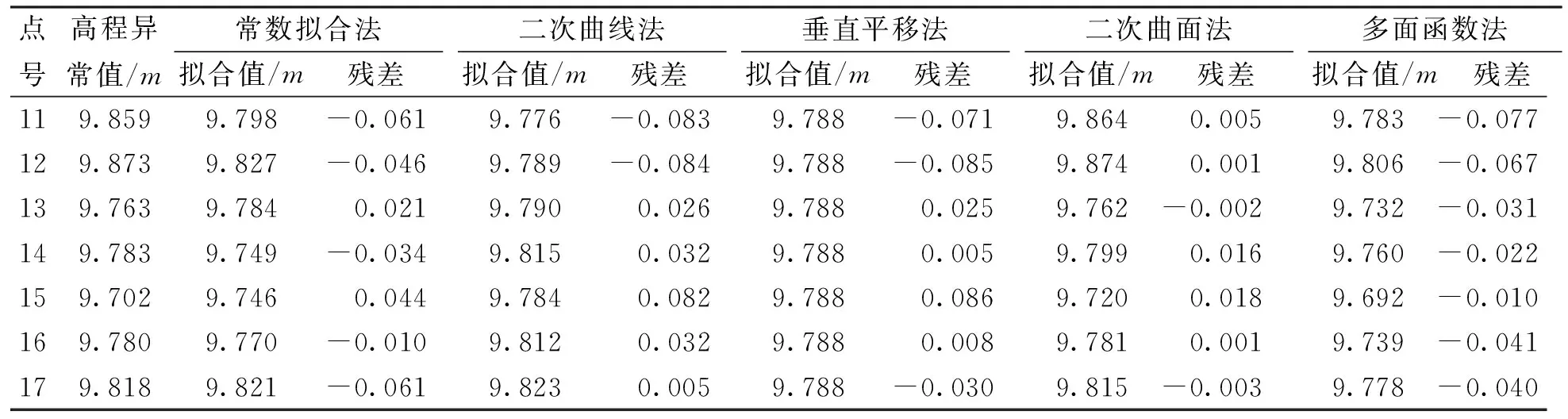
表2　各模型拟合结果

表3　各模型残差对比

2.3结果分析

由表2、表3可以看出,本算例中,二次曲面拟合法的残差及中误差明显小于其它几种方法,精度高于其它方法,拟合效果最为理想,达到四等水准测量的要求。

常数拟合法是根据待拟合点周围部分已知点的高程异常,加权平均求得该点的高程异常,能在一定程度上体现出地形因素对高程异常的影响;当控制点成线状分布时可采用曲线拟合法,而在成面状分布地区则不适合,拟合效果较差;垂直平移法由于只是简单地用已知点平均高程异常值替代待拟合点的高程异常,所以拟合效果并不理想;核函数选取、拟合点的分布情况及特征点数等对多面函数拟合法精度影响较大,拟合效果也不是很好。

3　结束语

随着GPS技术的发展,其各种优势越来越明显,在区域内用其优化甚至替代水准测量有很大的可行性。根据以上对GPS高程拟合的论述并结合具体的实验分析,可以得到如下几点经验:

1) 在地形起伏不大的区域范围内,通过选取合适的数学模型,GPS高程拟合可以获得比较高的精度,可极大减少水准测量的工作量,提高工作效率。

2) 二次曲面拟合法所需已知点少,适合于高程变化比较平缓的区域,在实际工作中操作性较强。

3) 高程异常受多种因素影响,通过函数模型进行拟合是一种纯数学方法,模型误差不可避免。实际应用中,在模型以及计算数据选取等方面需综合考虑各类因素的影响,应多进行比较、分析,尽可能提高拟合精度。

[1]陈安平,李红伟.GPS高程拟合方法的比较研究[J].测绘地理信息,2013,38(3):32-35.

[2]雷晓霞.基于重力与GPS水准组合法的大地水准面精化研究[D].西安:长安大学,2005:8-15.

[3]王岩,刘茂华,党永超,等.小地区GPS高程拟合的方法研究与实施[J].测绘通报,2012(S):66-68.

[4]高原,张恒璟,赵春江,等.多项式曲面模型在GPS高程拟合中的应用[J].测绘科学,2011,36(3):179-181.

[5]王峰,王 冉,崔锦龙,等.GPS高程拟合方法及其拟合精度对比[J].全球定位系统,2012,37(4):86-89.

[6]马鸿炜,郭金运,李国伟,等.一种区域似大地水准面模型拟合方法分析[J].海洋测绘,2014,34(1):8-11.

[7]雷伟伟,郑红晓.二次曲面拟合法在区域似大地水准面精化中的应用[J].测绘与空间地理信息,2008,31(6):38-40.

[8]张红华,孙月文.GPS高程拟合方法及精度分析[J].测绘与空间地理信息,2014,37(2):132-134.

[9]李景卫,杨荫奎,高建,等.GPS高程拟合中多面函数及二次曲面函数的比较与分析[J].山东冶金,2006,28(3):42-43.

Study and Comparison of GPS Elevation Fitting

ZHANG Piya1,NIU Chong2

(1.SchoolofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China;2.GeologicalSurveryingandMappingInstituteofShandongProvince,Jinan250001,China)

In the GPS measurement applications,we can’t directly use the GPS geodetic height, it must be converted by height fitting. Therefore, how to use GPS elevation fitting seek normal height is an important direction for the application research of geomatics. This paper discusses the theoretical basis of common GPS elevation fitting model, through examples of a comparative analysis of the applicability and reliability of several models, and finally draw some useful conclusions.

GPS; elevation fitting; constantfitting; curve fitting; surface fitting

2016-03-00

P228.4

A

1008-9268(2016)03-0105-04

张丕亚(1992-),男,硕士生,主要研究方向为现代测量数据处理。

牛冲(1989-),男,工程师,主要从事工程测量、变形监测等方面研究。

doi:10.13442/j.gnss.1008-9268.2016.03.022

联系人： 张丕亚E-mail:zpy2011@163.com