基于神经网络的卫星钟差预报及误差控制

朱陵凤,李超,刘利,李晓杰,郭睿

(北京卫星导航中心,北京 100094)



基于神经网络的卫星钟差预报及误差控制

朱陵凤,李超,刘利,李晓杰,郭睿

(北京卫星导航中心,北京 100094)

针对卫星钟差预报误差随时间不断变大问题,提出了基于BP神经网络的卫星钟差预报误差控制方法。该方法利用神经网络强大的非线性映射能力,对历史时段钟差拟合残差及当前时段钟差预报误差进行训练,得到拟合残差与预报误差的映射关系,据此根据当前时段的拟合残差预测未来时段的预报误差,将其补偿到未来时段钟差预报钟差结果中去,以实现未来时段卫星钟差预报误差的有效控制。为验证该方法的可行性和有效性,利用实测的COMPASS导航卫星钟差数据进行钟差预报精度分析,结果表明,神经网络可有效控制卫星钟差预报误差、提高卫星钟差预报精度。

神经网络;卫星钟差;COMPASS;预报

0　引　言

受限于国土地理分布的限制,区域导航系统的地面部分采用区域监测网,非地球同步轨道的导航卫星会运行到地面监测站的不可视弧段内,此时,导航卫星星载原子钟与系统时间之间的同步只能由卫星钟自己维持,因此,必须对导航卫星钟差进行预报[1]。鉴于原子钟物理特性与二阶多项式的吻合性,通常使用二阶多项式模型进行卫星钟差预报,然而,在轨运行的导航卫星星载原子钟频率高且非常敏感,极易受到太空环境及其自身因素的影响,因此,传统的二阶多项式模型很难预测其细致的变化规律,导致预报误差随预报时间不断变大,不能满足实际应用中的精度要求。

近年来,部分学者将灰色系统和Kalman滤波器[2]用于卫星钟差预报,取得了一些进展。灰色系统在数据量少的情况下预报优势明显,但是不同的灰色系统模型指数系数对预报精度有着非常大的影响,传统的灰色系统模型指数系数通常固定为一个常量,容易导致很大的误差,甚至是错误[3];Kalman模型中只考虑了钟差的确定性部分,将随机性部分简单视为白噪声处理,一定程度上降低了卫星钟差预报精度。

神经网络的原理是通过非线性基函数的线性组合实现从输入空间到输出空间的非线性转换,可逼近任意非线性映射,突破了建立参数模型的传统做法,在非线性预测方面优势明显。空间复杂运行环境下的卫星,其钟差是一类非线性较强的时间序列,对钟差序列进行预报,实质上就是找出从输入空间到输出空间的非线性映射关系。因此,神经网络特别适合于类似于钟差序列的非线性时间序列的预报[4]。然而,神经网络具有易陷入局部极小点和训练性能低等弊端,针对这些弊端,文献[5]利用RBF神经网络进行卫星钟差预报,达到了学习训练速度和收敛速度都很快的效果,但是预估精度低于传统二次多项式模型;文献[6]提出了基于一次差方法的小波神经网络钟差预报算法,使得模型结构简单,预报精度高于常用的二次多项式模型和灰色模型;文献[7]采用“滑动窗”划分数据,利用神经网络预测小波分解和去噪后的钟差序列各层系数,更精确地把握钟差序列复杂细致的变化规律,从而更好地逼近钟差序列,得到了较好的预报精度。

本文以多项式模型为基础,采用历史钟差多项式模型拟合残差和当前钟差多项式模型预报误差作为训练样本,训练得出二者间的映射关系,利用映射关系对当前钟差多项式模型拟合残差进行预测,得到未来时刻的多项式模型预报误差,将其补偿到未来时刻的多项式模型预报钟差中去。为了准确探测出不同时长的钟差变化规律,在训练样本的时长选择中采用了样本资料与预报等时长的策略,并对训练样本进行归一化处理以提高训练性能,取得了很好的效果。

1　训练样本准备

设t1,t2,…,tn历史时刻对应的钟差为x1,x2,…,xn,钟差的二阶多项式拟合模型可表示为

(1)

式中: a0、a1和a2为拟合系数; ei为模型误差。

上式可表示为矩阵形式

X=Ha+e,

(2)

式中: X为n维观测向量; a为3维未知参数向量; e为n维误差向量; H为3n维设计矩阵,可表示为

(3)

(4)

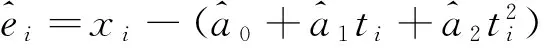
(i=1,2,…,n).

(5)

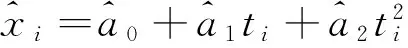
(i=n+1,n+2,…,n+m).

(6)

若已知tn+1,tn+2,…,tn+m时刻的钟差为xn+1,xn+2,…,xn+m,由下式可得钟差预报误差序列ΔXn+1,ΔXn+2,…,ΔXn+m

(i=n+1,n+2,…,n+m).

(7)

2　神经网络建模

神经网络作为一种新兴的建模工具,特点在于处理非线性、高维性的问题时不需要准确知道输入输出函数的结构参数,只需通过训练来掌握它们之间的内在关系,即可获得正确的映射关系,其优势在于不确定性关系的控制和预测。

鉴于这些优势,利用BP神经网络对历史钟差拟合残差和钟差预报误差进行建模。BP神经网络是一种多层网络的“逆推”学习算法,由输入层、输出层和中间层(隐层)组成。隐层可以有多个。每一层包含若干个神经元,同一层中的神经元彼此不相连,不同层间的神经元可有相连。其结构如图1所示。

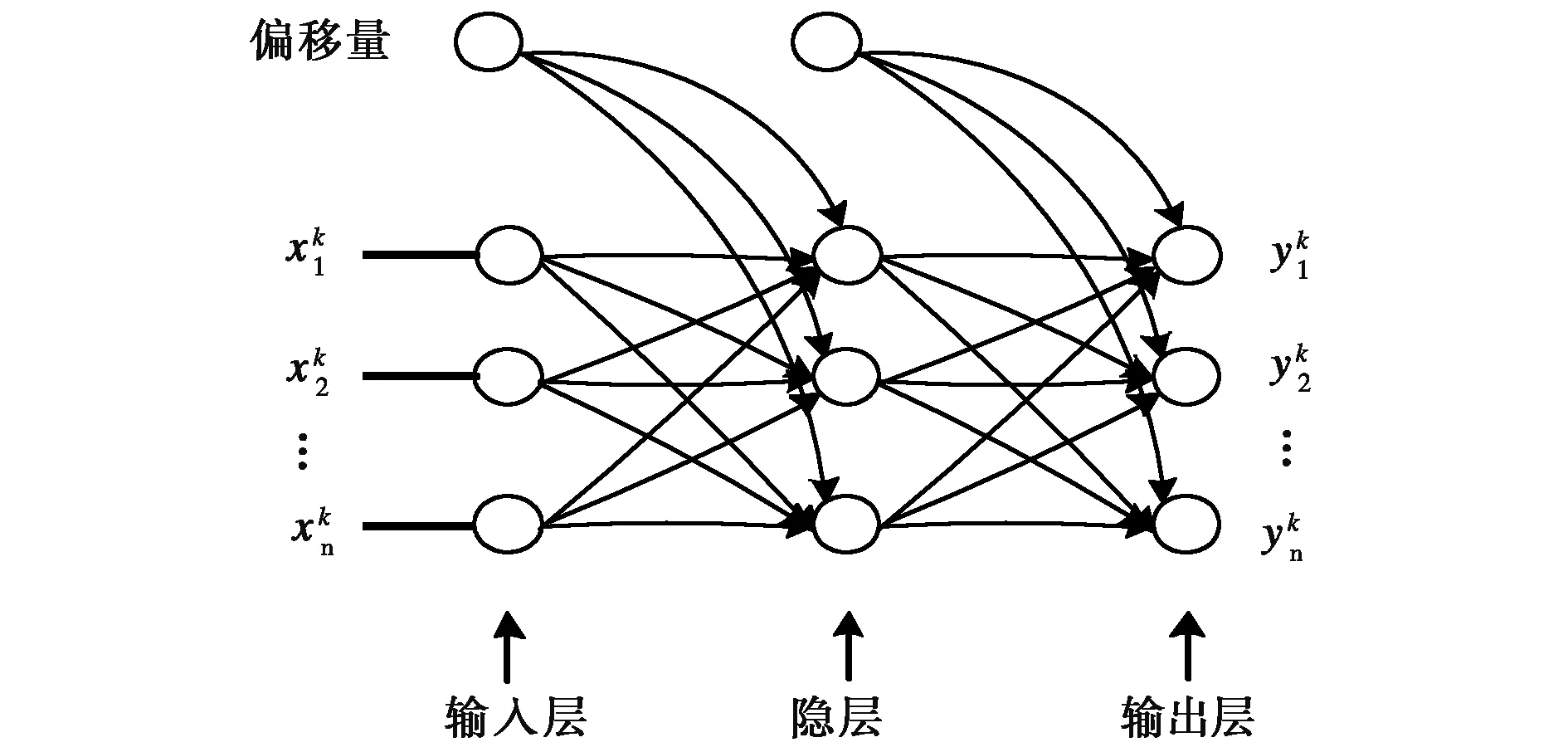
图1　BP神经网络的基本结构图

BP神经网络的基本单位是神经元,神经元接收输入信号,通过激活函数输出信息。为了表现出网络的非线性特性,隐层节点的传递函数往往为非线性的。较常用的非线性激活函数为对数双曲线函数和正切双曲线函数。对于输出层,可以采用线性激活函数,也可采用前两种非线性的激活函数。值得注意的是,如果输出层使用非线性激活函数,那么网络的输出将被限制在一定的范围内;如果输出层使用线性激活函数,那么网络的输出的范围将相对较大。

考虑到钟差长期预报情况下,训练样本中的预报误差在数值上远大于历史钟差拟合残差,为方便数据处理和提高训练性能,对训练样本进行归一化处理,将两者除以各自的最大值,如此二者的变化范围都统一在±1之间,再对二者进行建模。

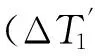
图2　神经网络模型训练及补偿示意图

3　算例分析

采用COMPASS系统GEO-05卫星2015年8月12/13/14/15日连续4天共96小时的实测钟差数据进行神经网络控制钟差预报误差试验。先利用传统二阶多项式对GEO-05卫星钟差进行预报,再利用神经网络预测钟差预报误差,将其补偿到传统模型预报结果中,评估补偿后的预报精度提高幅度。采用均方根误差(RMS)来衡量模型的预报精度, 其公式为

(8)

05卫星预报钟差。

具体方案如下:钟差数据资料采样间隔为1s,时间跨度选为3n小时,将资料分为三段,即第一段n小时、第二段n小时和第三段n小时。采用二阶多项式模型对第一段n小时钟差数据资料建模,预报第二段n小时的钟差,根据实测钟差值,可得到第一段n小时钟差拟合残差和第二段n小时钟差预报误差,对二者进行训练得到n小时预报误差与拟合残差的映射关系;采用二阶多项式模型对第二段n小时钟差数据资料建模,预报第三段n小时的钟差,根据实测钟差值,可得到第二段n小时钟差拟合残差,利用训练得到的映射关系可由第二段n小时钟差拟合残差预测得到第三段n小时钟差预报误差,将其补偿到第三段n小时的二阶多项式预报钟差结果中去。以第三段n小时的实测钟差为真值,评估第三段n小时钟差的二阶多项式模型预报精度及神经网络补偿后的钟差预报精度,并对补偿效果进行分析。本文设定n等于2小时、6小时、12小时、18小时、24小时和30小时共6种情形,计算结果如表1和图3所示,其中,PM表示二阶多项式模型预报结果,NN表示BP神经网络补偿后的预报结果。

由表1和图3可见: 1) 采用传统二阶多项式模型,2、6、12、18、24和30小时的卫星钟差预报误差RMS分别为0.35ns、1.01ns、1.36ns、3.24ns、4.72ns和6.75ns,随着预报时长的增加,预报误差不断增大; 2) 采用神经网络补偿后,2、6、12、18、24和30小时的卫星钟差预报误差RMS分别为0.08ns、0.24ns、0.38ns、0.49ns、0.55ns和0.60ns,随着预报时长的增加,预报误差的增大趋势被有效控制在1ns范围内; 3) 相同预报时长情况下,神经网络补偿后的预报精度明显提高,2、6、12、18、24和30小时的卫星钟差预报精度分别提高了0.27ns、0.77ns、1.02ns、2.75ns、4.17ns和6.15ns,补偿比例分别为77.14%、76.24%、75.00%、84.88%、88.35%和91.11%,可见,预报时间超过12小时的情况下,预报时间越长,补偿效果越明显。

表1　卫星钟差预报误差RMS统计结果/ns

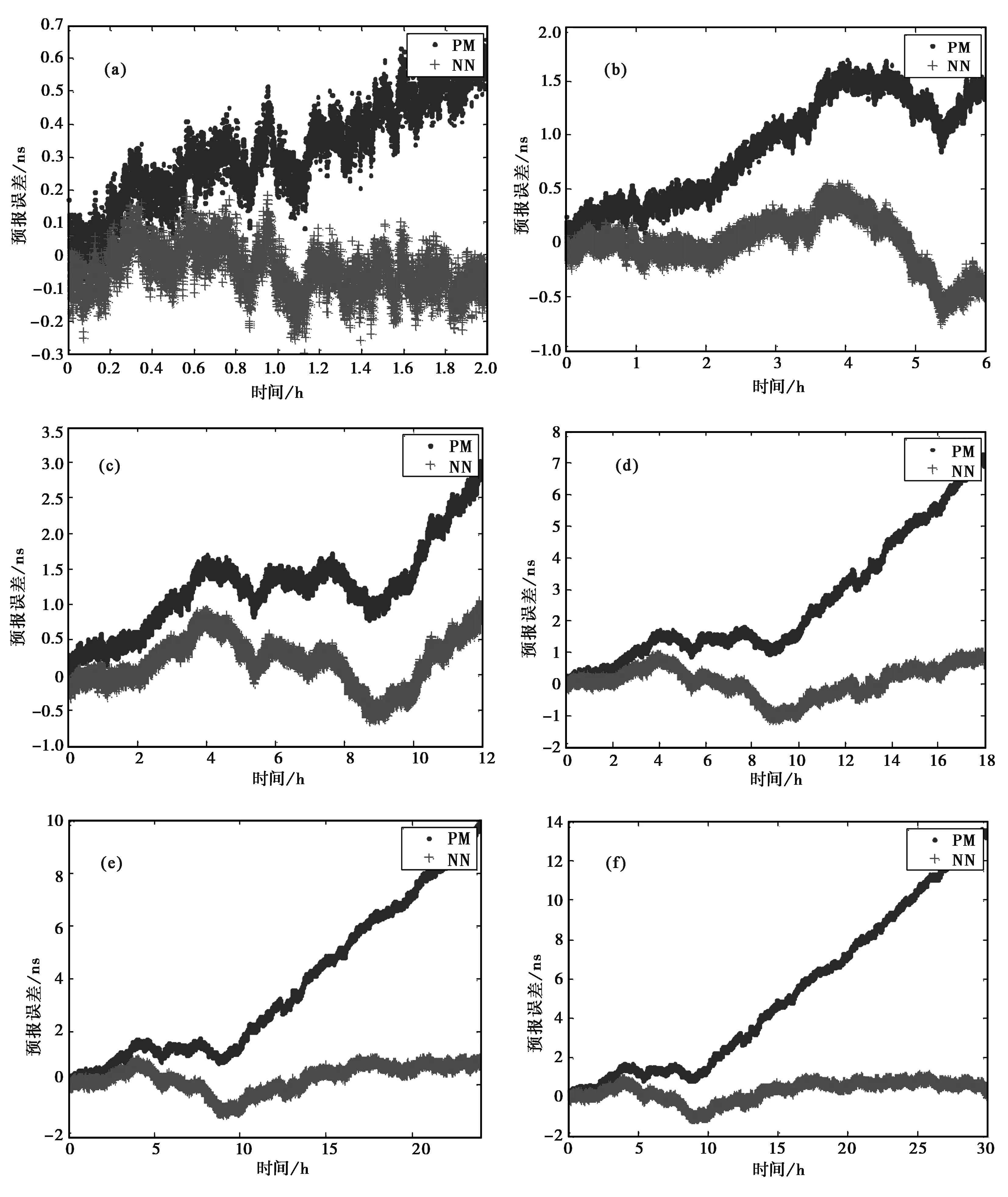
图3　卫星钟差预报误差 (a) 2 h; (b) 6 h; (c) 12 h; (d) 18 h; (e) 24 h; (f) 30 h

4　结束语

本文将BP神经网络应用于导航卫星钟差预报误差控制,通过训练历史钟差拟合残差和当前钟差预报误差,得出二者之间的映射关系,根据当前钟差拟合残差预测出未来钟差预报误差,并将其补偿到未来钟差预报结果中去,有效控制钟差预报误差随时间不断变大的趋势。COMPASS导航卫星实测数据验证结果表明:神经网络将导航卫星钟差6种不同时长的预报误差均控制在1 ns范围内,30小时的预报精度高达0.6 ns,高于相同预报时长的其他方法预报精度,验证了本文方法的合理性和有效性。

然而,利用BP神经网络进行样本训练时,对训练样本的前提要求是连续且规律性强。本文将钟差拟合残差和钟差预报误差作为训练样本,故要求二者是连续且规律性强。文中选取的试验样本是全天候连续观测的GEO卫星钟差,对于非全天候连续观测的导航卫星,可以考虑采用星间链路补充地面不可视弧段,确保卫星钟差数据连续性,再考虑使用BP神经网络进行钟差预报。此外,考虑到星载原子钟长期运行过程中,其物理特性变化有一定的随机性,因此,基于规律性强的历史样本预测方法也存在一定的局限性,下一步将继续探索其他处理方法的可行性。

[1]吴海涛,李孝辉,卢晓春,等.卫星导航系统时间基础[M].北京:科学出版社,2011.

[2]刘建成,杨睿峰,徐赟,等.基于Kalman滤波器的卫星钟差预报精度分析[J].全球定位系统,2012,37(4):1-5.

[3]路晓峰,杨志强,贾小林,等.灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2008,33(5):492-495.

[4]郭承军,滕云龙.神经网络在卫星钟 差短期预报中的应用研究[J].测绘科学,2011,36(4):198-200.

[5]张景元.基于神经网络的卫星钟差预报研究[J].计算机工程与设计,2014,35(9):3254-3257.

[6]王宇谱,吕志平,陈正生,等.卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013,42(3):323-330.

[7]郭承军,滕云龙.基于小波分析和神经网络的卫星钟差预报性能分析[J].天文报,2010,51(4):395-403.

Satellite Clock Prediction and Error Control Based on Neural Network

ZHU Lingfeng,LI Chao,LIU Li,LI Xiaojie,GUO Rui

(BeijingSatelliteNavigationCenter,Beijing100094,China)

Aiming at improving the predicting precise of satellite clock error, method of controlling satellite clock error will be mentioned in this paper which is also based on BP neural network theory. Considering of the nonlinearity mapping ability of neural network, this method compares residual errors, which is created according to outdated statistics, with current errors to find the potential relation between these 2 errors. After the comparison, this paper gets mapping relation between residual errors and current errors. This paper assumes this relation also exist between current errors and the future errors. To prove this assumption is workable, this paper analyzes the predicting precise of satellite clock error through the statistics of COMPASS satellite clock error. The analysis shows this method is feasible and effective, which means neural network can improve the predicting precise of satellite clock error.

Neural network; satellite clock error; COMPASS; prediction

2016-01-22

国家高技术研究发展计划(批准号:2014AA123102).

P228.4

A

1008-9268(2016)03-0068-05

朱陵凤(1983-),女,硕士,工程师,主要从事卫星导航系统时间同步技术研究。

李超(1981-),男,硕士,工程师,主要从事卫星导航用户终端测试技术研究。

刘利(1976-),男,博士,高级工程师,主要从事卫星导航系统总体技术研究。

李晓杰(1984-),女,博士,工程师,主要从事卫星导航系统精密定轨技术研究。

郭睿(1982-),男,博士,高级工程师,主要从事卫星导航系统总体技术研究。

doi:10.13442/j.gnss.1008-9268.2016.03.014

联系人： 朱陵凤 E-mail: 50903763@qq.com