拱、弯梁与索空间组合桥梁的成桥调索方法

梁　栋，马金龙，刘志强，王云燕

(1.河北工业大学　土木工程学院，天津　300401；2.河北省土木工程技术研究中心，天津　300401)



拱、弯梁与索空间组合桥梁的成桥调索方法

梁栋1,2，马金龙1，刘志强1，王云燕1

(1.河北工业大学土木工程学院，天津300401；2.河北省土木工程技术研究中心，天津300401)

利用修正的Ernst 公式考虑吊索几何非线性，以影响矩阵法为理论基础，以目标索力差值和拱肋横向位移为双控制目标，采用以弯曲应变能最小为约束条件的最小能量法进行拱、弯梁与索空间组合结构的索力优化计算，约束最优方法求解出拱、弯梁与索空间组合结构的施调索力、最优调索顺序以及调索过程索力控制终值。结合世界上跨度最大的拱、弯梁与索组合结构的工程调索实例，利用有限元法实现了调索计算。结果表明，该方法所确定的调索张拉顺序、施调索力能够满足调索施工控制要求，最终成桥状态亦达到设计要求，为今后类似结构的调索工程提供了重要参考。

桥梁工程；索力调整；影响矩阵理论；空间受力体系；最优调索顺序

0　引言

随着计算手段与施工技术的提高，利用拉索或吊杆形成的空间结构在工程中日趋广泛，如昌平综合体育馆、张家口通泰大桥等。桥梁结构，特别是受力复杂的拱、弯梁与索空间组合结构在长期的运营过程中，结构的内力和线形都会不断地发生变化。当变化超出了设计预期，甚至造成了严重病害时，就需要进行调索，以恢复其合理的成桥状态[1]。在这个过程中，设计一套合理的调索方案，以满足组合结构桥梁在运营阶段的受力要求，并实现预测的长期变形特性，是调索工作的重要前提[2]。

国内外开展索力调整的主要计算方法包括最小二乘法、弯曲能量最小法、弯矩最小法和影响矩阵法。最小二乘法是反复迭代计算后使误差的平方和达到最小[3]；弯曲能量最小法是使结构的弯曲应变能这一目标函数达到最小；而弯矩最小法则是以弯矩平方和作为目标函数，使之达到最小；影响矩阵法将截面内力、应力或位移等受调向量通过影响矩阵与索力这一施调向量联系起来，可同时对多种目标函数进行优化[4]。

针对通泰大桥的调索工作，本文利用修正的Ernst 公式考虑该桥拉索几何非线性，以影响矩阵理论为基础，以目标索力差值和拱圈横向位移作为控制双目标，求解了施调索力、最优调索顺序以及调索过程中的索力控制终值。

1　通泰大桥调索工程概况

通泰大桥位于河北省张家口市，是世界上跨度最大的下承式钢结构吊索拱桥，主跨190 m，双向6车道，总宽34 m，设计行车速度60 km/h，抗震烈度7度。主梁跨径190 m，位于R=600 m的平曲线上，两端均设限位设施，并分别设置固定支座和活动支座；拱肋跨径180 m，矢高62.1 m，矢高比1/2.897 7，在平面上为直拱。拱肋斜跨主梁两侧，通过28根长短不同，方向各异的空间吊索与主梁连接，构成了受力复杂的大跨径拱、弯梁与索空间组合结构，通泰大桥如图1所示。该桥自2008年12月建成通车以来，经过长年的使用，特别是一些超限重车的通行，使通泰大桥出现了包括支座脱空在内的病害。为防止病害进一步发展，进而危及主桥的结构安全，本文开展了相应的调索计算及调索施工控制作为病害处理措施的主要部分。

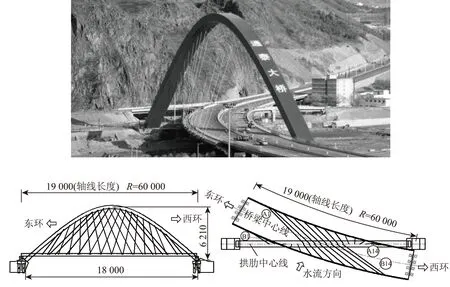
图1　拱、弯梁与索空间组合的通泰大桥(单位：cm)Fig.1　Arch, curved beam and cable composed Tongtai bridge (unit:cm)

2　通泰大桥调索分析计算

2.1索单元的几何非线性处理

由于拉索是通泰大桥的主要受力构件，因此拉索在计算过程中的分析就成为重要内容之一。为了提高拉索计算的精确性，人们研究了等效弹性模量法、多节点单元、多根直链杆法、多根直梁单元、曲线梁单元和忽略抗弯刚度的柔索单元等[5]来模拟柔性拉索构件。

通泰大桥共有28根长短不同、方向各异的拉索，最长索为76.8 m，最短索为29.6 m，拉索的外径有100，105 mm和110 mm 3种规格，按不同角度和位置分别布置在拱肋两侧，在分析中有必要考虑其几何非线性，以保证调索工作的顺利实施。目前，等效弹性模量法由于其操作简便、精度可靠等特点，是索构件几何非线性处理过程中比较常用的方法。Ernst 在1965 年给出了著名的Ernst 公式[6]，即用两节点杆单元弹性模量的改变来模拟索的张力与位移之间的非线性关系。

(1)

式中，Eeq为等效弹性模量；E0为索的材料弹性模量；L为索的水平投影长度；γ为索的单位体积质量，即重度；σ为索的应力。

如果考虑拉索倾角引起的切向自重荷载，修正的Ernst 公式[7]为：

(2)

式中，σ1为索变形后的应力，

结合通泰大桥的工程实际，本文采用式(2)中修正的Ernst 公式来考虑其吊索的几何非线性。

2.2考虑目标索力差值和拱顶横向位移的影响矩阵法

影响矩阵法[8-10]是一种常用的索力优化方法，它将优化的多种目标函数统一用索力变量与广义影响矩阵表示，实现了用一种方法对多种目标函数进行优化，同时由于编程方便，因此获得了广泛应用。

由于通泰大桥受力的空间性，特别是弯梁与直拱肋斜交，在左右对称性方面牵一发而动全身，在调索过程中要确保拱肋的横向稳定性。基于此，本文针对通泰大桥建立了综合考虑目标索力差值和拱顶横向位移的双目标影响矩阵法。已知每根拉索的初始索力Fc和目标索力Tm，在拉索张拉之前的原始状态下，分别给每一拉索施加单位力1，分别计算出该单位力对索力和拱顶横向位移的变化量，即索力差值和拱顶横向位移的影响矩阵。

桥梁结构体系在调索之前已然形成，此状态可作为通泰大桥的既有初始状态。该状态下，索力的初始状态向量Fc为：

(3)

令通泰大桥的索力影响矩阵为Mc，则Mc为28×28阶的矩阵。其中元素Mcij表示在j号拉索增加单位力1的索力时，i号索索力的变化值。设索力目标值为FT，索力调整值为FS，则

(4)

则，索力调整值FS为

(5)

令通泰大桥的拱顶横向位移影响向量为Ma，Ma为28×28阶的正对角阵，其中元素Majj表示在j号拉索增加单位力1的索力时，拱顶横向位移的变化值。当索力调整值为FS时，则拱顶横向位移的变化值δa为：

(6)

2.3调索顺序的优化问题

假设通泰大桥处于线弹性状态，即满足线性叠加原理，求出施调索力向量后，采用任何一种张拉顺序都能使该桥的索力达到目标值。为保证调索过程中的结构安全和施工方便性，必须找到一种最优的张拉顺序以保证调索施工期间的结构安全[11]。在此，本文确定了调索后的实际索力与设计值之间的差值Fcs和拱顶横向位移δa两个目标要同时达到最小，因此目标函数向量为：

(7)

根据通泰大桥主梁抗弯、抗剪、拱肋抗压、抗弯、拉索抗拉的计算要求，以及结构的刚度要求等32个约束不等式，约束可表示为：

(8)

可以将上述双目标优化问题归结为以下向量极小化问题，即

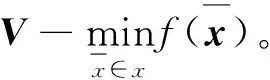
(9)

对向量极小化问题的求解有多种方法，本文选用评价函数法中的线性加权和法进行计算。限于篇幅，本文在此只给出该方法的主要计算步骤[12]如下：

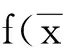
(2)评价函数u(f)是综合了两个目标函数后得到的数值函数，因此，向量极小化问题转化成了极小化公式的数值函数。

(3)为避免目标函数的“淹没现象”，对目标函数向量实行无量纲化，使各目标函数均处于同一数量级。

(4)采用均差排序法在有效解中挑选一个使目标函数(7)都尽可能小的解，从而使其有一个最好的协调。

2.4有限元分析模型

本文采用有限元分析软件Midas-Civil进行通泰大桥调索过程的仿真分析。以设计施工图提供的截面、材料与尺寸为依据，利用空间梁单元模拟拱肋和主梁，共443个空间梁单元；吊索模拟为空间桁架单元，共28个，通过在材料特性中人为定义吊索对应桁架单元的弹性模量，即利用式(2)来实现对其非线性的考虑；拱脚处采用固结，主梁两端采用单向竖向支撑；在主梁和拱肋与吊索连接位置分别建立节点，采用Midas弹性连接中的刚性连接与梁单元连接。选取拱脚端部连线为x轴，连线中点为坐标原点，建立整体结构的空间三维模型如图2所示。

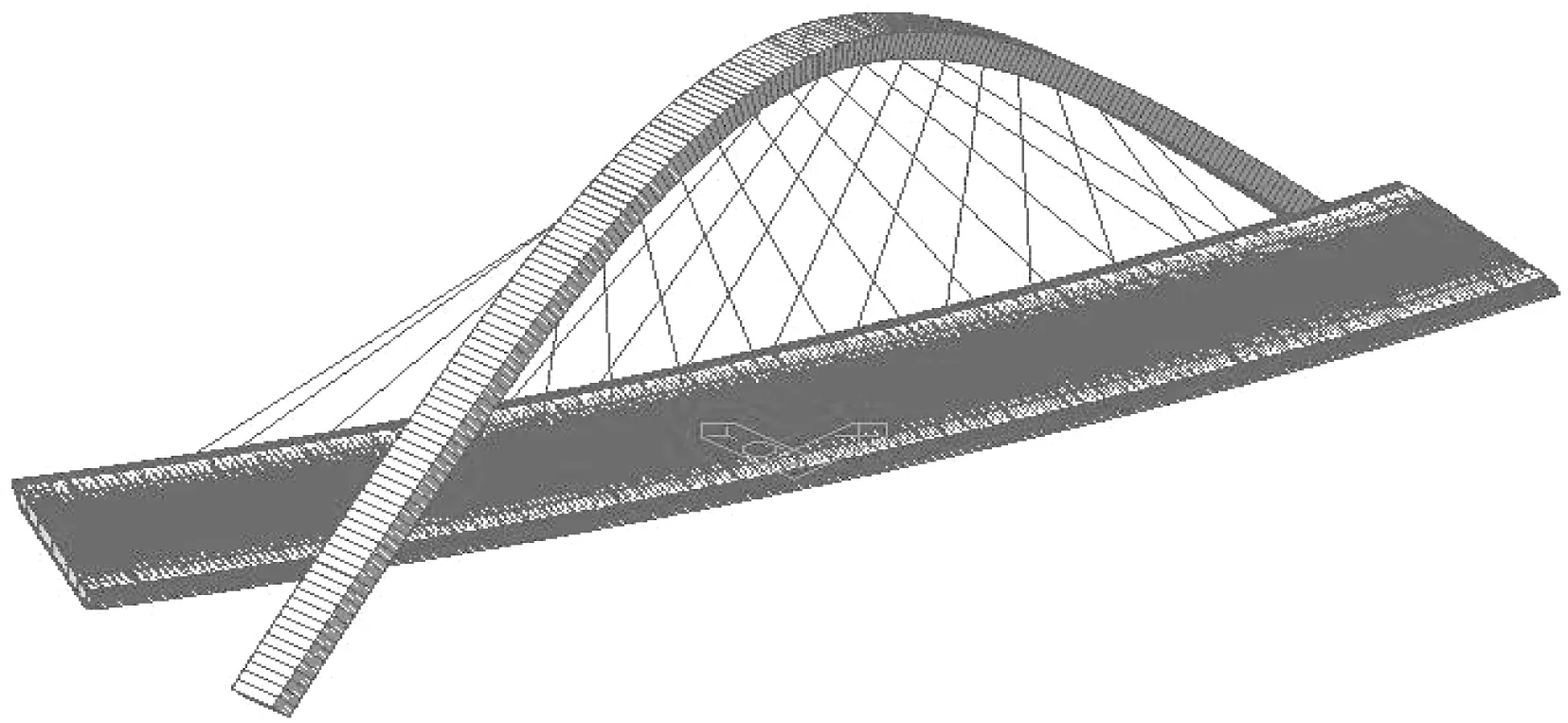
图2　通泰大桥Midas-Civil有限元模型Fig.2　Midas-Civil FE model of Tongtai bridge

钢箱梁和拱肋主体结构及临时匹配件均采用Q345，其弹性模量取为2.1×105N/mm2，泊松比取为0.3，线膨胀系数取为1.2×10-5。吊索钢丝采用直径为7mm的高强度低松弛镀锌钢丝，标准强度为1 670MPa，弹性模量取为1.95×105N/mm2，泊松比取为0.3，线膨胀系数取为1.2×10-5。

在调索仿真分析过程主要考虑了结构自重、二期恒载、梁端压重和温度荷载。其中利用密度修正考虑横隔梁等连接板件的自重；二期恒载和梁端压重均按图纸取值；温度荷载按照实际情况考虑整体升降温。

恒载自身扭矩：由于弯主梁用空间梁单元模拟时，不能考虑由于弯曲引起的恒载自身扭矩，因此分析时额外施加了恒载扭矩。其中，钢箱梁恒载自身扭矩为22.583(kN·m)/m，铺装和栏杆自身扭矩之和为18.174(kN·m)/m。

3　索力调整

3.1拉索初始索力

准确的索力测试是调索工作的基础。本文中受施工条件限制，拉索端部的长达2m的套筒并不能完全拆除，拉索在振动时不可避免地要与套筒接触，该桥拉索的计算长度和边界条件具有很大的不确定性。因此利用常用的频率法测定既有索力必然带来较大误差。例如，通泰大桥最短索A14的理论计算索长为29.6m，千斤顶实测索力值为270.0kN，用频率法测定的索力为319.6kN，相差18.4%。

基于成本和时间的考虑，本文利用液压千斤顶实测了通泰大桥的实际索力。利用千斤顶实测成桥索力的主要步骤是：(1) 将临时螺母装置分别与吊索锚杆和千斤顶连接；(2) 将液压千斤顶顶在锚箱上，开始张拉千斤顶；(3) 锚固螺母与锚箱刚刚脱离时的压力表数值所代表的拉力即为实际索力。设计索力Ff与千斤顶测定索力Fj的对比见表1。

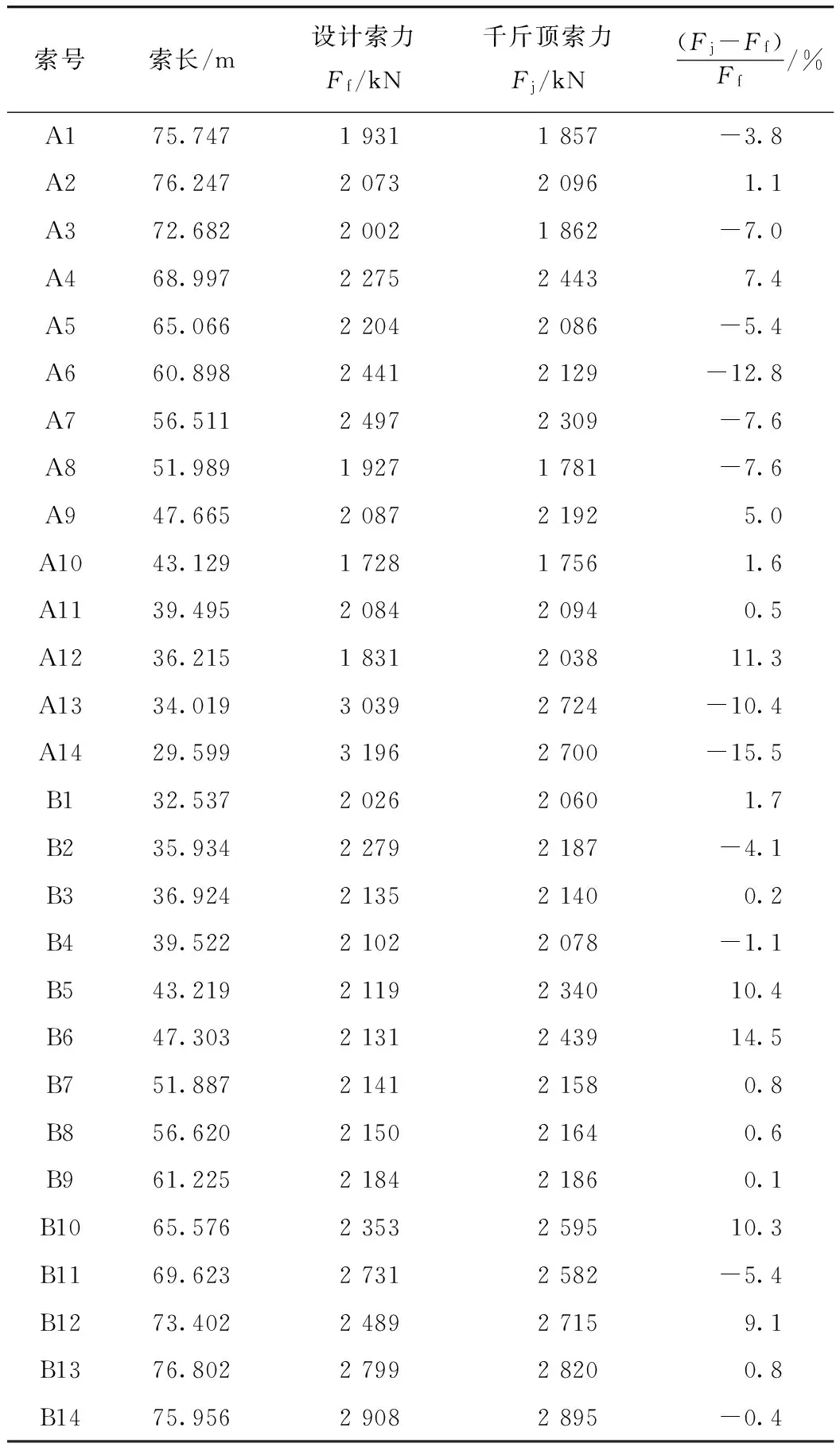
表1　调索前的实际索力Tab.1　Real cable forces before adjustment

由表1可以看出，初始状态的索力与设计值的最大相对误差达到了15.5%，有14根吊索的索力偏差超过了设计所要求的5%以内，因此非常有必要开展调索工作。

3.2吊索非线性的影响

本文以表1中调索以前的实测索力为依据，图3给出了实测索力、桁架单元索力与利用修正Ernst 公式(2)所得索力。

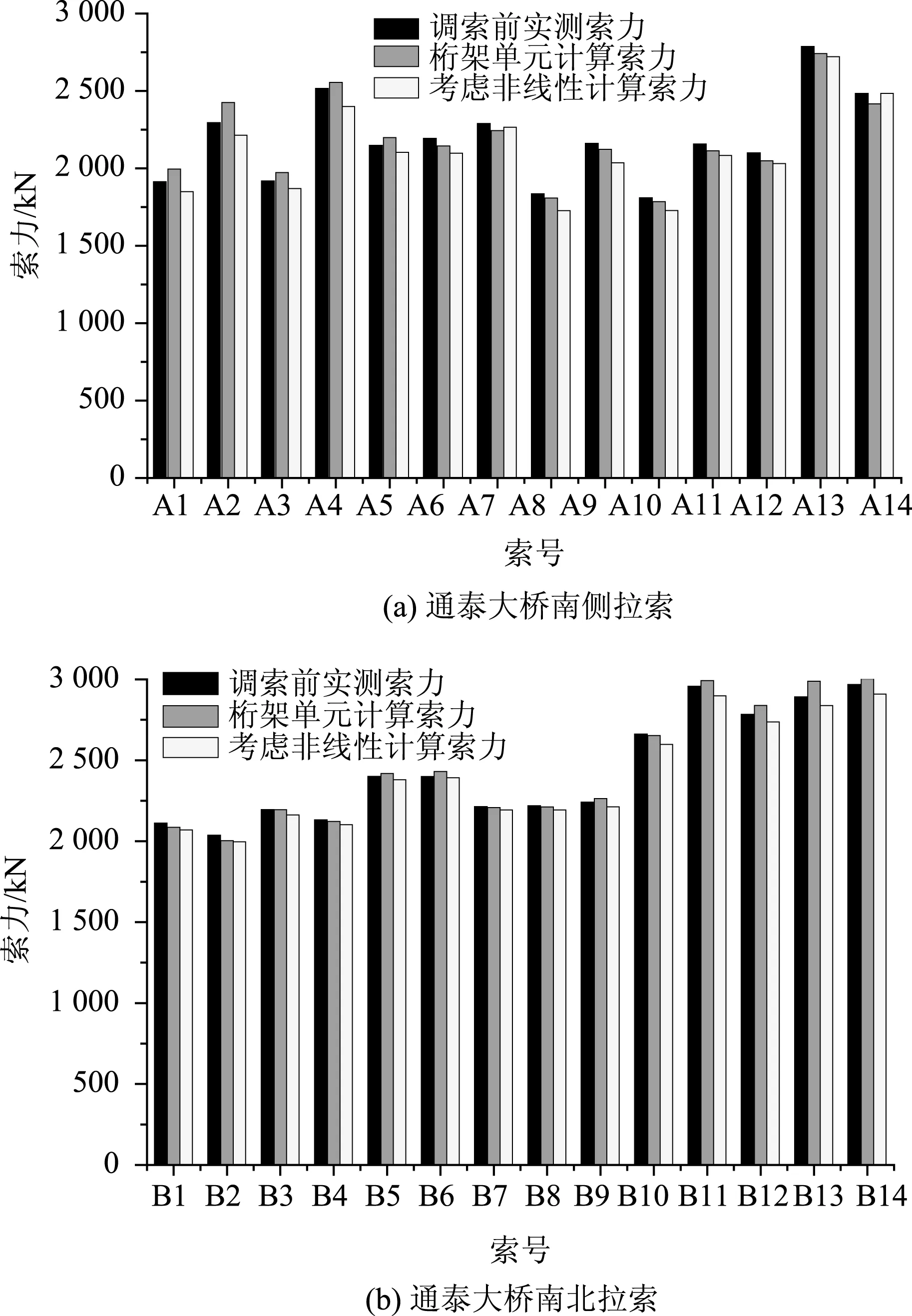
图3　几何非线性对索力的影响Fig.3　Effect of geometric nonlinearity on cable force

由图3可知，利用修正Ernst公式(2)所得到的索力与实测索力的误差最大值为3.0%，而直接利用桁架单元所得到的索力与实测索力之间误差的最大值达到了9.4%。同时，随着吊索长度的增加，误差也逐渐增大。

3.3调索方案的确定

根据设计要求，本次索力调整的原则是平均索力，即将超过5%的相对误差平均到邻近的拉索上，使全部拉索的相对误差小于5%即可。综合考虑拱肋的横向稳定性和现场调索施工的方便性，基于本文第2节的考虑，采用影响矩阵法确定施调索力，根据双目标优化并利用均差排序法确定最优的施调顺序。最后，所确定的各根拉索施调索力和施调顺序为A2：-198.5 kN→A9：-216.1 kN→B5：-180 kN→B6：-170 kN→B11：-180 kN→ B12：-190 kN。仿真整个调索过程得到的最终索力如图4所示。

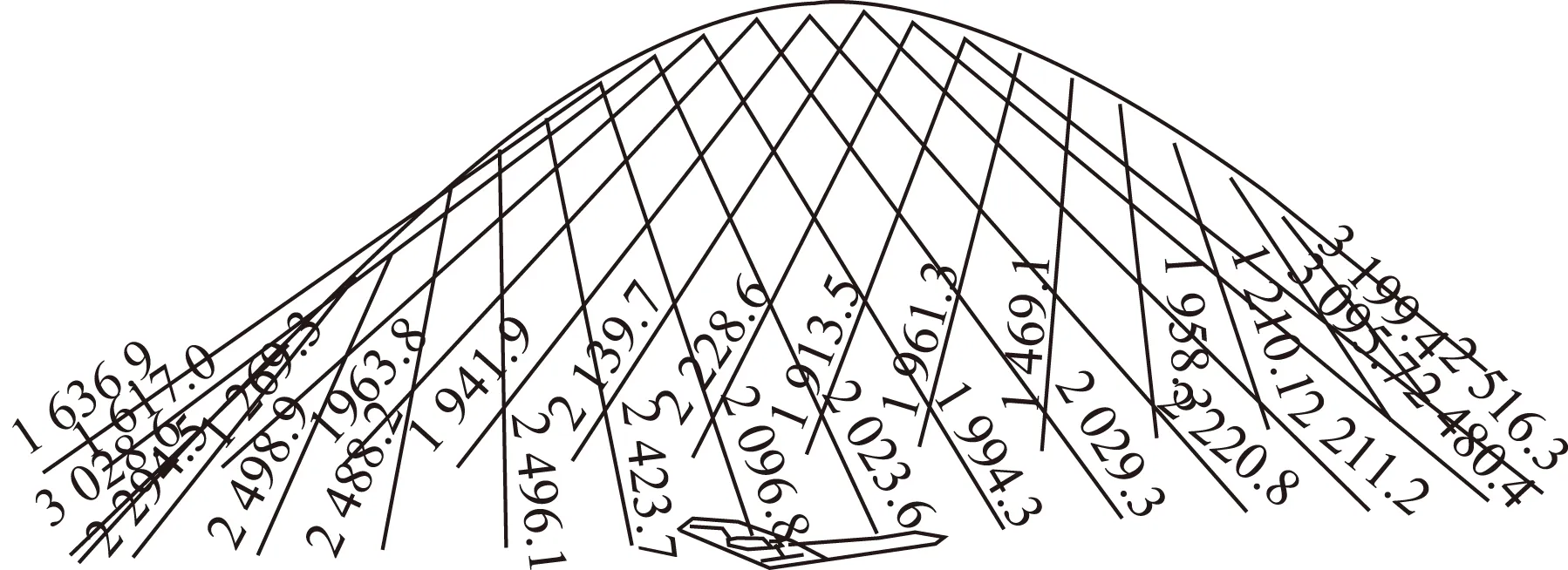
图4　张拉 B12后的索力值(单位:kN)Fig.4　Cable forces after tensioning Cable B12(unit:kN)

3.4调索结果

按照3.3节中的调索方案实施调索工作，设计索力、调索前索力和调索后索力的对比如图5所示。由此可以看出，在自重荷载作用下，调索后的索力与设计值的最大相对误差为4.31%，最小相对误差达到了-2.02%。经过索力调整，通泰大桥的实际索力值与设计值满足相对误差不超过 5%的范围要求，完全达到了预期目的。

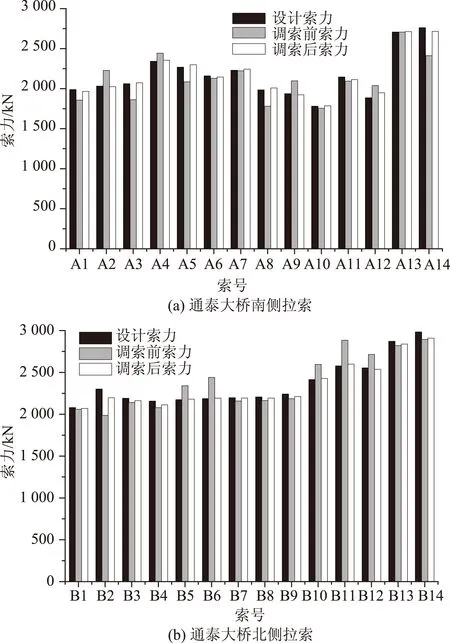
图5　调索前、后的索力对比图Fig.5　Comparison of cable forces before and after adjustment

调索完成后，荷载作用下的索力变化与设计值相差不大。图6给出了以调索后自重状态索力为初始条件，公路-I级荷载产生的索力及其与设计值的对比。由图6可知，公路-I级荷载产生的索力仅相当于自重状态产生索力的0.5%～1.5%，占比很小；调索后公路-I级荷载产生的索力与设计值相差很小，最大差值是A5索的4.7%。因此，调索工作同样优化了公路-I级使用荷载下的索力，达到了预期目的。

在自重荷载作用下，分别利用图5所示的设计索力、初始索力和调索后索力，可得该桥在调索前、后的主梁、拱肋的内力及位移，及其与设计状态的对比情况如表2所示。由表2可知，调索工作优化了通泰大桥主梁和拱肋的受力性能。

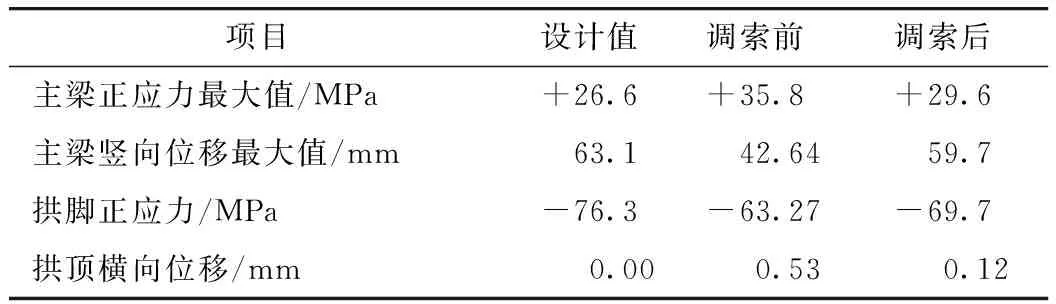
表2　调索前后的拱、梁受力性能Tab.2　Mechanicle performance of arch and girder before and after adjustment

注：+为拉应力，-为压应力。

5　结论

张家口通泰大桥的调索实践为今后类似桥梁结构的调索工程提供了重要的参考，结果表明：

(1)在计算吊索拉力时利用了考虑垂度影响的Ernst 修正公式，以影响矩阵理论为基础，以目标索力差值和拱圈横向位移作为控制双目标，是保证通泰大桥索力调整成功的理论基础。

(2)索力调整后，自重状态下的全桥索力接近目标值，索力分布趋于均匀。

(3)与直接采用桁架单元相比，利用修正的Ernst 公式(2)考虑吊索几何非线性可获得更为精确的计算结果。

(4)调索工作使桥面线形、拱圈横向位移等指标得到明显的改善，改善了主梁与拱肋的受力性能。

References:

[1]刘雄, 钟新谷, 熊先兰,等. 基于无应力状态控制法的斜拉桥运营期调索计算方法研究[J]. 公路交通科技, 2015, 32(9):80-86.

LIU Xiong, ZHONG Xin-gu, XIONG Xian-lan, et al. Study of Cable Adjustment Calculation Method of Cable-stayed Bridge during Operation Period Based on Control Method of Unstressed State[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9):80-86.

[2]肖汝诚, 项海帆. 斜拉桥索力优化的影响矩阵法[J]. 同济大学学报:自然科学版, 1998, 26(3):235-240.

XIAO Ru-cheng, XIANG Hai-fan. Influence Matrix Method of Cable Tension Optimization for Cablo-stayed Bridges[J]. Journal of Tongji University: Natural Science Edition, 1998, 26(3):235-240.

[3]颜东煌, 李学文, 刘光栋,等. 混凝土斜拉桥合理成桥状态确定的分步算法[J]. 中国公路学报, 2003, 16(1):43-46.

YAN Dong-huang, LI Xue-wen, LIU Guang-dong, et al. Step-by-step Arithmetic for the Reasonable Finished Dead State of the Concrete Cable-stayed Bridges[J]. China Journal of Highway and Transport, 2003, 16(1):43-46.

[4]张熙胤, 陈兴冲, 王常峰. 梁拱组合桥吊杆力优化及工程应用[J]. 铁道建筑, 2014 (1):4-6.

ZHANGXi-yin,CHENXing-chong,WANGChang-feng.OptimizationofSuspenderForceofBeamArchCombinationBridgeandEngineeringApplication[J].RailwayEngineering, 2014 (1):4-6.

[5]梁立农, 韩大建. 索的非线性有限元与调索方法研究[J]. 工程力学, 2007, 24(11):146-152.

LIANGLi-nong,HANDa-jian.AStudyonNonlinearFiniteElementAnalysisforCableandAdjustmentMethodofCableForces[J].EngineeringMechanics, 2007, 24(11):146-152.

[6]FLEMINGJF.NonlinearStaticAnalysisofCable-stayedBridgeStructures[J].ComputersandStructures, 1979, 10(4): 621-635.

[7]金问鲁. 悬挂结构计算理论[M]. 杭州: 浙江科学技术出版社, 1981.

JINWen-lu.TheoreticalCalculationofSuspensionStructure[M].Hangzhou:ZhejiangScienceandTechnologyPress, 1981.

[8]肖汝诚, 郭文复. 结构关心截面内力、位移混合调整计算的影响矩阵法[J].计算结构力学及其应用, 1992, 9(1):91-99.

XIAORu-cheng,GUOWen-fu.InfluenceMatricesMethodforStructuralAdjustmentCalculationofInternalForcesandDisplacementsofConcernSections[J].ComputationalStructuralMechanicsandApplications, 1992, 9(1):91-99.

[9]孔繁龙. 影响矩阵法在施桥大桥吊杆二次调索中的应用[J]. 交通科技, 2012 (2):7-9.

KONGFan-long.ApplicationofInfluenceMatrixMethodtoSecondaryCable-adjustmentforShiqiaoBridge[J].TransportationScience&Technology, 2012 (2):7-9.

[10]杜蓬娟, 张哲, 黄才良. 斜拉桥成桥后误差调整的优化方法[J]. 哈尔滨工业大学学报, 2005,37(7):1016-1018.DUPeng-juan,ZHANGZhe,HUANGCai-liang.OptimizationMethodofErrorAdjustmentofCableStayedBridgeinFinishedState[J].JournalofHarbinInstituteofTechnology, 2005,37(7):1016-1018.

[11]霍学晋, 高立强, 伍星. 多拱肋蝶形拱桥的施工索力优化研究[J]. 公路交通科技, 2011, 28(3):82-89.HUOXue-jin,GAOLi-qiang,WUXing.StudyonOptimizationofConstructionCableForcesforMulti-ribButterfly-shapedArchBridge[J].JournalofHighwayandTransportationResearchandDevelopment, 2011, 28(3):82-89.

[12]许铁生, 杜永峰, 胡秀宣.RC梁系结构双目标优化设计的研究[J]. 建筑结构, 1993 (10):46-50.

XUTie-sheng,DUYong-feng,HUXiu-xuan.ResearchofDoubleTargetOptimizationDesignofRCBeamStructure[J].BuildingStructure, 1993 (10):46-50.

A Cable Adjustment Method for Arch, Curved Beam and Cable Composite Bridge in Completion State

LIANG Dong1,2, MA Jin-long1, LIU Zhi-qiang1, WANG Yun-yan1

(1. School of Civil Engineering，Hebei University of Technology，Tianjin 300401，China；2. Hebei Provincial Civil Engineering Technology Research Center，Tianjin 300401，China)

Considering geometric nonlinearity of cable, based on the theory of influence matrix method, and taking the differences between the target cable tension and lateral displacement of arch rib as dual control objectives, the optimized calculation of cable tension of spatial composite structure of arch, curved beam and cable is conducted by using the modified Ernst formula and the minimum energy method which regarded the bending strain energy minimization as constraints. The adjusted cable tension forces, the optimal order of cable tension adjustment, and the final control value of cable force in adjustment process are solved by the optimal constraint method. Combining with the cable tension adjustment examples of the largest spatial arch, curved beam and cable composite structure in the world, the cable tension adjustment calculation is conducted with finite element method. The result shows that the optimal order of cable tension adjustment and the adjusted cable tension forces meet the control requirements of cable adjustment, and the completion state eventually meets the design requirements. This method provided an important reference for similar structures of cable tension adjustment in the future.

bridge engineering; cable tension adjustment; theory of influence matrix; spatial force system; optimal order of cable tension adjustment

2015-08-15

国家自然科学基金项目(50808063)

梁栋(1976-)，男，河北南宫人，博士，教授.(13622114075@139.com)

U443.38

A

1002-0268(2016)08-0086-06

doi:10.3969/j.issn.1002-0268.2016.08.013