结合面底部带门式钢筋的铰接空心板桥受力性能参数分析

陈康明，吴庆雄，黄宛昆，陈宝春

(福州大学　土木工程学院，福建　福州　350116)



结合面底部带门式钢筋的铰接空心板桥受力性能参数分析

陈康明，吴庆雄，黄宛昆，陈宝春

(福州大学土木工程学院，福建福州350116)

为研究结合面底部带门式钢筋的铰接空心板桥铰缝受力性能，以带深铰缝构造的铰接空心板桥为研究对象，总结了我国铰接空心板桥铰缝构造的演变过程，进行了一跨8 m跨径的空心板桥非线性有限元参数分析，分析了不同铰缝构造参数下空心板桥铰缝构造的开裂荷载、裂缝分布等破坏模式，讨论了现有铰缝构造的改进措施。结果表明：在结合面底部增设门式钢筋，不能明显地提高铰缝构造的开裂荷载，但可以提高铰缝构造的通缝荷载，延缓空心板与铰缝结合面竖向通缝和纵桥向通缝的形成；增大门式构造钢筋直径对结合面开裂荷载、通缝荷载和最终的裂缝分布没有明显改善；增大混凝土强度对空心板与铰缝结合面的改善作用有限；提高空心板与铰缝结合面黏结力可以提高结合面通缝荷载，并能减小裂缝分布范围；现有文献提及的3种铰缝钢筋布置形式和增大钢筋直径的方法较难从根本上改善结合面受力性能。

桥梁工程；空心板桥；参数分析；铰缝构造；门式钢筋；非线性有限元

0　引言

我国从20世纪60年代开始使用铰接空心板桥，铰接空心板桥在我国中小跨径桥梁中得到广泛应用。早期建设的大量空心板桥在投入实际运营多年后出现了诸多病害，以铰缝病害为主，导致桥梁的横向传力性能下降，甚至形成“单板受力”[1-2]。针对铰接空心板桥的铰缝构造病害问题，王渠[3]、陈悦驰[4]等以铰缝和空心板的结合面底部未设置门式钢筋的铰接空心板为研究对象，通过试验和有限元分析得到在车辆荷载作用下最先发生开裂的部位是空心板与铰缝结合面，该部位是铰接空心板最薄弱的部位；铰缝开裂先于空心板开裂，铰缝会出现结合面竖向通缝和纵桥向通缝。吴庆雄[5]和王峰[6]以铰缝和空心板的结合面底部增设门式钢筋的铰接空心板为研究，通过试验和有限元分析得到，虽然设置了门式钢筋，但是铰缝和空心板的结合面仍是最薄弱的部位；在空心板与铰缝结合面底部布设门式钢筋，虽不能明显提高铰缝构造的开裂荷载，但可以限制结合面裂缝沿竖向和纵桥向的开展。

已有的研究成果给出了铰接空心板桥的受力性能和破坏模式，但尚未明确各铰缝构造参数对受力薄弱的铰缝构造受力性能的影响。因此，本文首先总结了我国铰接空心板桥铰缝构造的演变过程，然后以带深铰缝构造的铰接空心板桥为研究对象，进行铰缝构造的参数分析，并对现有铰缝构造的改进措施进行讨论，研究结果可为后期改进铰缝构造、提高空心板桥受力性能提供参考和依据。

1　铰接空心板桥铰缝构造的演变

随着我国技术水平的发展，公路桥涵设计规范的更新和提高，铰接空心板桥构造也在不断地改进[7]。选取在国内应用时间最长、具代表性的交通部颁布的铰接空心板标准图为对象，分为旧标准图和新标准图两种进行对比分析。在此，旧标准图为依据1985年和1989年交通部颁布的《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTJ 023—85)[8]和《公路桥涵设计通用规范》(JTJ 021—89)[9]制定的桥涵标准图[10-11]，新标准图为依据2004年交通部颁布的《公路桥涵设计通用规范》(JTG D60—2004)[12]和《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[13]制定的桥涵标准图[14]。

1.1铰缝尺寸

铰缝构造沿着板高方向的铰槽部分深度示意，见图1。新、旧标准图中铰槽深度和铰槽占板高的比例对比见表1。在旧标准图中，铰接钢筋混凝土空心板桥的铰缝铰槽构造的深度随着板高的增加而增加，属于深铰缝构造范畴；然而预应力混凝土空心板桥的铰槽构造深度随着板高的增加保持不变。对于新标准图，由于《公路桥涵设计通用规范》(JTG D60—2004)[13]第9.2.9条规定铰槽的深度宜为预制板高的2/3，故铰槽构造深度随着板高的增加而增加，始终大于67%(2/3)。

图1　铰槽深度Fig.1　Depth of hinged joint表1　新、旧标准图铰槽深度和铰槽占板高比例对比Tab.1　Comparison between hinge groove depths and its accounted percentages in new and old standard drawings

跨径/m铰槽深度/cm占板高比例/%旧标准新标准旧标准新标准629/--83/--834/-30/-85/-71/-1039/4338/4887/8676/801349/43-/5889/72-/8316-/43-/68-/57-/8520-/43-/83-/45-/87

注：/前的数值为铰接钢筋混凝土预制板桥；/后的数值为铰接预应力混凝土预制板桥。

1.2铰缝钢筋布置

旧标准图中铰缝钢筋分3类，即预埋在空心板内的顶部连接钢筋N1(①号钢筋)、剪刀钢筋N2(②号钢筋)和纵向钢筋N3(③号钢筋)，见图2(a)。

新标准图中的铰缝钢筋在空心板与铰缝结合面的底部均需增设如图2所示的门式钢筋N4。

图2　铰缝钢筋构造Fig.2　Steel rebar structure in hinged joint

1.3铰缝混凝土强度

旧标准图中钢筋混凝土预制板的铰缝混凝土强度为30号(C28)，预应力混凝土预制板的铰缝混凝土强度为40号(C38)；新标准图中钢筋混凝土预制板的铰缝混凝土强度为C40，预应力混凝土预制板的混凝土强度为C50。

此外，在新标准图的设计说明中有提到“铰缝混凝土可选择抗裂、抗剪、韧性好的钢纤维混凝土”，说明在条件允许时可考虑将钢纤维混凝土应用于实际工程中，使铰缝能更好地满足实际需求。

2　有限元计算模型

2.1计算对象

本文以新标准图中8 m铰接空心板桥为原型，选取5片空心板、4道铰缝和10 cm厚的桥面铺装层组成分析模型。横断面布置见图3。

图3　有限元分析模型横断面布置(单位：cm)Fig.3　Cross-sectional layout of FE model (unit: cm)

空心板采用C30混凝土，铰缝和桥面铺装层采用C40混凝土。钢筋等级均为HRB335级。

空心板沿纵桥向为等截面，构造尺寸如图4所示。铰缝构造见图5(a)，构造钢筋分3类，分别为沿纵桥向间距为15 cm的剪刀钢筋(①号钢筋)、纵向受力钢筋(②号钢筋)和空心板与铰缝结合面底部门式钢筋(③号钢筋)。此外空心板内预埋顶部连接钢筋(④号钢筋)，钢筋构造见图5(b)。在桥面铺装层的中部布置一层10 cm×10 cm的钢筋网。

图4　空心板截面(单位：cm)Fig.4　Cross-section of hollow slab (unit: cm)

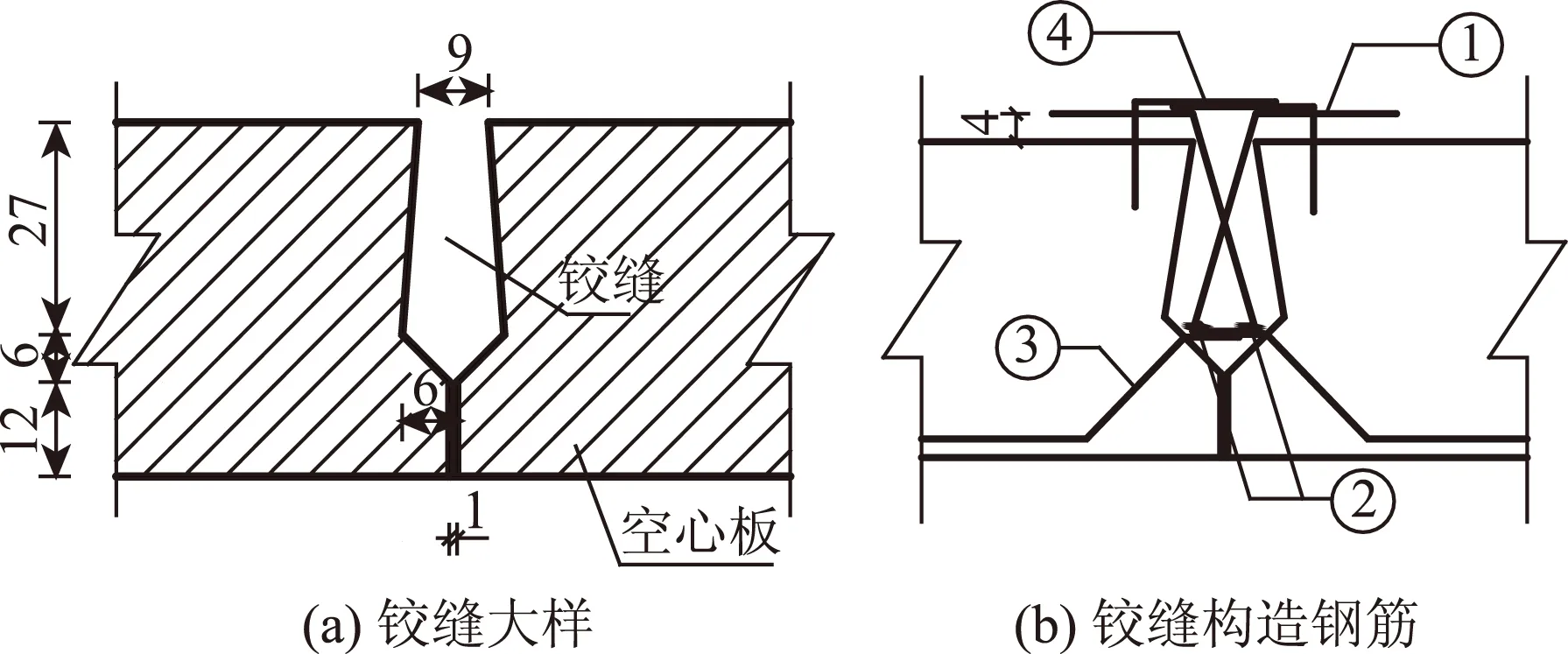
图5　铰缝构造(单位：cm)Fig.5　Hinged joint structure (unit: cm)

采用公路-I级标准车辆荷载进行加载，根据最不利原则选取标准车辆较重的后轴进行加载。同时将荷载转换为均布荷载，根据JTG D62—2004[13]的规定，后轴轮胎着地横桥向宽度为0.6 m，纵桥向长度为0.2 m。车辆轮载F沿纵桥向最不利作用位置在跨中处，加载位置见图6(a);车辆轮载F沿横桥向对称布置，加载位置见图6(b)。

图6　车辆荷载加载布置(单位：cm)Fig.6　Layouts of vehicle load (unit: cm)

2.2有限元模型

利用ABAQUS通用程序建立有限元模型，全桥有限元模型见图7(a)、(b)所示。模型采用C3D8单元(八节点三维线性六面体单元)模拟空心板、铰缝和桥面铺装层，如图7(c)、(d)所示。由于在空心板和铰缝处需要针对接触进行模拟，故在空心板靠近铰缝处的区域将网格细化。其中，空心板单元边长在1～3 cm之间，铰缝单元边长在0.5～3 cm之间，铺装层单元边长在3～12 cm之间。采用T3D2单元(三维三节点桁架单元)建立空心板底部受力主筋和空心板与铰缝结合面门式钢筋。采用Interaction中的Embedded功能将钢筋嵌入到混凝土实体单元中。

图7　空心板桥有限元计算模型Fig.7　FE model of hinged hollow slab bridge

采用混凝土结构设计规范(GB 50010—2002)[15]中塑性损伤模型模拟混凝土的塑性行为。钢筋应力-应变关系采用理想弹塑性模型，弹性模量Es=2.0×105MPa，泊松比μ=0.3，屈服应力为335 MPa。

限制模型两侧布设板式橡胶支座处空心板的竖向、横桥向和纵桥向位移，其中竖向抗压刚度、横桥向和纵桥向抗剪刚度根据文献[16]设置。

2.3空心板与铰缝构造的结合面模拟

不考虑空心板顶面和铰缝顶面与桥面铺装层底面间的相对滑移，模型中采用区域绑定约束Tie连接，使上述各接触面的平动和转动相互耦合。

空心板与铰缝的结合面属于新、老混凝土结合面，如图8所示，新老混凝土黏结强度可以分为法向轴拉黏结强度ft和两个沿着结合面切向方向的黏结剪切强度τx，τy。

图8　结合面黏结强度方向Fig.8　Direction of bonding strength on junction surface

法向轴拉黏结强度采用文献[17-18]的计算方法，即：选取轴拉强度标准值较小的空心板侧混凝土(C30)的轴拉强度标准值的70%。

(1)

关于黏结剪切强度，采用叶见曙等[20]提出的普通混凝土铰缝抗剪强度计算公式：

(2)

式中fs为铰缝和空心板混凝土中强度值较小的混凝土轴心抗压强度值。

根据材性试验结果选取轴心抗压强度值较低的空心板侧混凝土的轴心抗压强度值用于计算，即：τx=τy=0.01×28.9=0.29。

新老混凝土结合面的黏结滑移关系是进行有限元模拟的重要依据，主要包括黏结滑移曲线的类型、结合面上两个方向的剪切强度τx和τy、结合面法向轴拉强度ft、结合面黏结滑移刚度K和最终的滑移值与峰值应力对应滑移值Su/So。

根据文献[19]可以采用双折线模型来模拟空心板与铰缝结合面的黏结滑移关系，并通过统计得到关于空心板与铰缝结合面黏结滑移曲线相关参数的取值范围：结合面法向轴拉黏结滑移曲线类型与沿着结合面表面方向的抗剪黏结滑移曲线类型相同；空心板与铰缝结合面的黏结滑移刚度K可取5～15 MPa/mm 之间，计算模型中取10 MPa/mm；最终滑移值和峰值应力对应的滑移值之比可取1.5～3.0，计算模型取2.0。将法向和切向的黏结滑移曲线见图9。

图9　结合面黏结滑移曲线Fig.9　Curves of bonding-slip on junction surface

2.4有限元模型的验证

文献[6]对本文研究对象进行了试验研究。图10为模型计算结果与试验结果的对比，包括跨中截面空心板荷载-挠度曲线、最不利的2号铰缝底部荷载-横向张开量曲线和结合面门式钢筋荷载-应变曲线，图中所示荷载为单个加载点(后文若无特别注释，荷载值的定义与此相同)，因对称性，图10(a)、(c)中仅画出1～3号板和1、2号铰缝的曲线。可以看出，有限元计算值与试验值吻合良好，相同荷载下各空心板跨中挠度误差小于8.6%，2号铰缝跨中截面底部横向张开量误差小于13.4%，结合面底部门式钢筋应变误差小于12.6%。这说明该非线性有限元模型可以用于铰接空心板桥受力性能的分析。

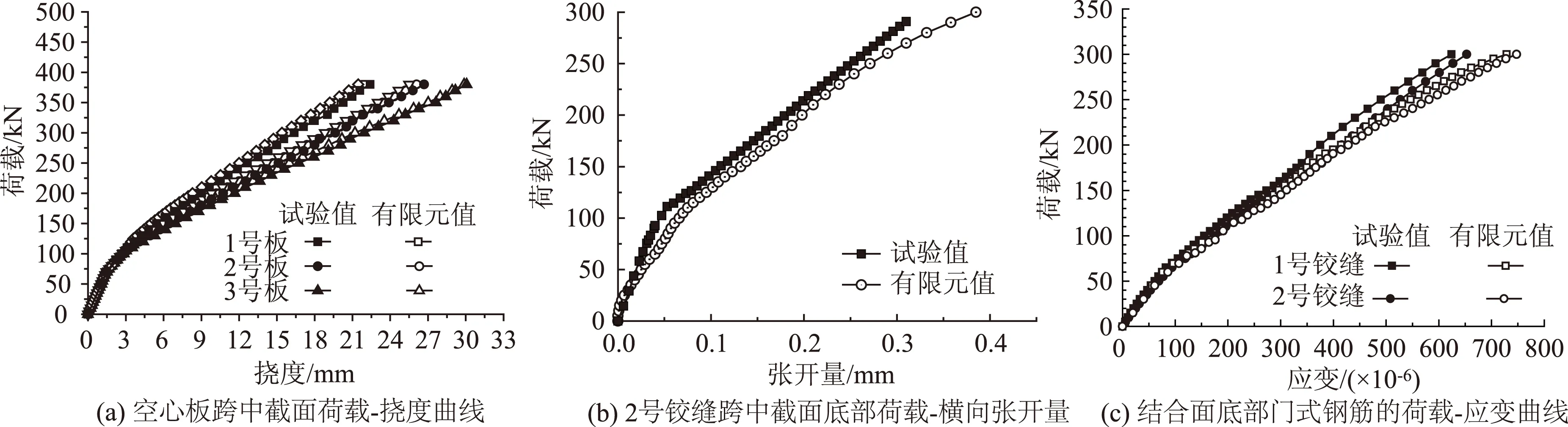
图10　有限元计算结果与试验结果对比Fig.10　Comparison between FE calculated values and experimental values

3　铰缝构造参数分析

3.1参数选择与说明

根据第1节的统计结果可知，新、旧标准图中铰接空心板桥在构造上有两个重要区别之处在于新标准图中空心板与铰缝结合面底部增设了门式钢筋，并提高了铰缝及空心板混凝土强度等级。根据文献[5-6]，由于铰缝与空心板结合面黏结力较弱，结合面是空心板桥最薄弱的位置。因此，本文选取门式构造钢筋、铰缝混凝土强度等级以及结合面黏结力进行参数分析，了解这些铰缝构造参数对铰接空心板桥受力性能的影响。

根据2.2节对新、旧混凝土结合面模拟方法的叙述可知，在3个方向的黏结强度非耦合的情况下，当某点处的3个方向中有某个方向的相对位移量超过峰值应力所对应的位移限值时，即认为该处的黏结发生失效。从图9可知，法向和切向的相对位移量限值分别为0.14 mm和0.03 mm。根据文献[5-6]分析结果可知，以竖向滑移量为指标时，结合面处的超限分布范围最广，对应的开裂荷载最小；根据图11中8个结合面的编号，3#(4#)结合面先于其他结合面发生黏结失效，且黏结失效范围更大。因此，本文选取受力最不利的4#结合面，以竖向相对滑移量作为结合面黏结破坏失效指标，分析不同铰缝构造参数对空心板和铰缝受力性能和破坏模式的影响。

图11　结合面分布Fig.11　Distribution of junction faces

文献[5]和[6]分别进行了3片和5片8 m空心板桥的荷载试验，结果对比分析表明，空心板横桥向片数会影响分配至各片空心板的试验荷载，但对铰缝和空心板的受力性能和在各自极限荷载下破坏模式影响较小。以挠度最大空心板的荷载-挠度曲线和张开量最大铰缝的荷载-横向张开量为例，对比见图12。为明确空心板跨径的影响，本文根据第2节建模方法和加载方式，建立了5片20 m跨径的空心板桥，并将其计算结果与文献[5-6]对比。如图15所示，跨径对铰缝和空心板的受力性能和破坏模式影响也较小。因此，下文仅以文献[6]中的5片8 m空心板桥为研究对象进行参数分析。

图12　空心板跨径与片数影响Fig.12　Influence of span and transversal number of hollow slab

3.2门式钢筋

将结合面开裂荷载(结合面底部初裂时荷载)、通缝荷载(结合面裂缝贯穿到截面顶面，形成通缝时荷载)见图13，结合面竖向通缝纵向分布长度、结合面底部裂缝纵向分布长度见图14。

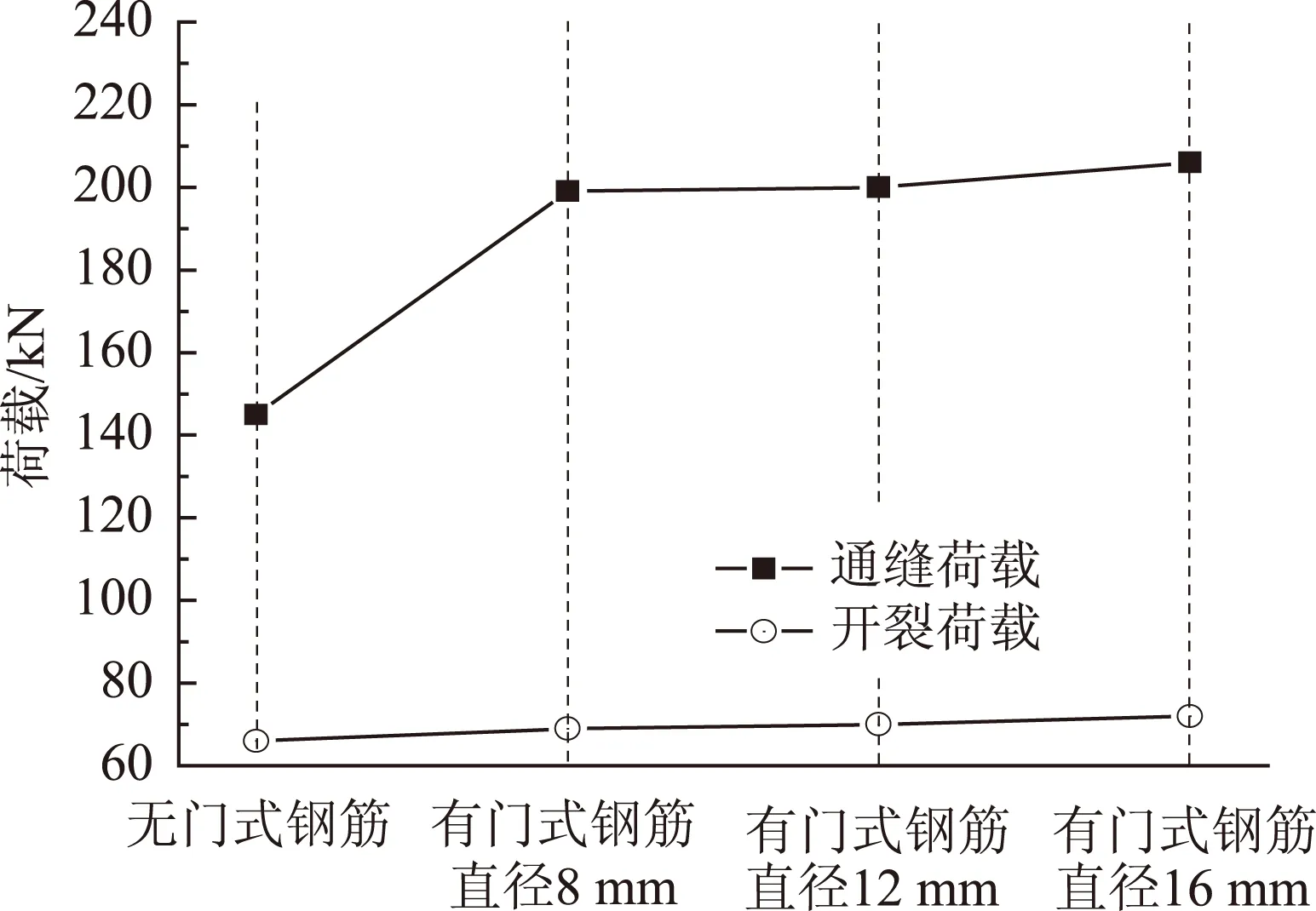
图13　不同门式钢筋直径下结合面开裂荷载和通缝荷载Fig.13　Crack loads and full-length crack loads of junction surface with different diameters of gate-type steel rebar

图14　不同门式钢筋直径下结合面竖向通缝和底部裂缝纵向分布长度Fig.14　Vertical full-length cracks and longitudinal cracks at bottom of junction surface with different diameters of gate-type steel rebar

从图13和图14可知，当结合面设置8 mm门式钢筋后，相对于无门式钢筋的空心板：开裂荷载由66 kN增加到69 kN，提高4.5%；通缝荷载由145 kN 提高到199 kN，提高37.2%；结合面竖向通缝的分布由跨中5 m范围减小到跨中1.4 m范围，减小72%；结合面底部裂缝纵向分布长度由通长8 m 改善到分布长度为5.4 m，减少48.1%。这是由于门式构造钢筋距空心板底面有一定距离，结合面底部还是空心板桥最薄弱部位，在外荷载作用下，仍然最先开裂。因此，在结合面增设门式钢筋，不能明显提高铰缝构造的开裂荷载。但是，由于门式钢筋能有效地连接空心板和铰缝，改善结合面受力性能，并承担部分弯矩和竖向剪力，使得门式钢筋可以延缓空心板与铰缝结合面竖向通缝和纵桥向通缝的形成。

从图13和图14可知，当门式钢筋的直径由8 mm 增加到16 mm：开裂荷载从69 kN提高至72 kN，提高4.3%；形成通缝荷载从199 kN提高至206 kN，提高3.5%；结合面竖向通缝的纵桥向分布范围由1.4 m减小到1.2 m，减少16.7%；结合面底部纵桥向裂缝分布范围由5.4 m减小到5.0 m，减少8%。这说明增大门式钢筋直径并不能进一步改善空心板与铰缝连接性能。同时，从图10(c)可以看出，直至空心板破坏，8 mm门式钢筋还处于弹性阶段，增大门式钢筋直径并不能承担更大荷载。因此，增大结合面门式钢筋直径对结合面开裂荷载、通缝荷载以及最终的裂缝分布没有明显的改善。

图15为铰缝跨中截面底部横向张开量曲线。可以看出，荷载达到300 kN时，设置8 mm门式钢筋后铰缝的横向张开量为不设置门式钢筋时的0.55倍。这是由于门式钢筋能有效地连接空心板和铰缝，改善结合面受力性能，延缓空心板与铰缝结合面竖向通缝和纵桥向通缝的形成。因此，门式钢筋可显著减小铰缝横向张开量。

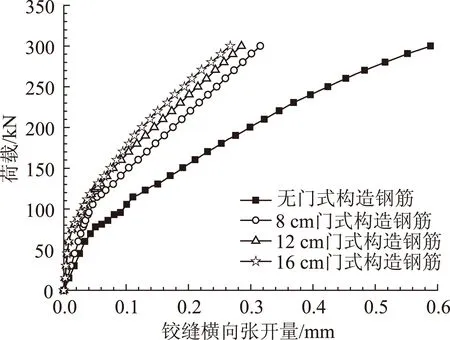
图15　不同门式钢筋直径下跨中铰缝横向张开量曲线Fig.15　Transverse opening curves of hinged joint at mid-span with different diameters of steel rebar

从图15可知，将门式钢筋的直径由8 mm增大到12 mm和16 mm，铰缝横向张开量分别减小了9%和15%，这说明增大门式钢筋直径并不能进一步改善空心板与铰缝连接性能，对减小空心板底部裂缝和结合面竖向通缝沿纵桥向分布范围的作用有限。因此，增大门式钢筋直径对限制铰缝横向张开量作用也有限。

以单位荷载作用于3号板时各板荷载横向分布系数为例，门式构造钢筋对荷载横向分布系数的影响如图16所示。当结合面设置8 mm门式钢筋后，相对于无门式钢筋的空心板，3号板荷载横向分布系数由0.240减小至0.226；当门式构造钢筋直径由8 mm 增大至16 mm时，3号板荷载横向分布系数仅由0.226减小至0.219。因此，增设门式构造钢筋可增强空心板间协同承载，但增大门式钢筋直径对改善空心板间协同承载的作用不大。

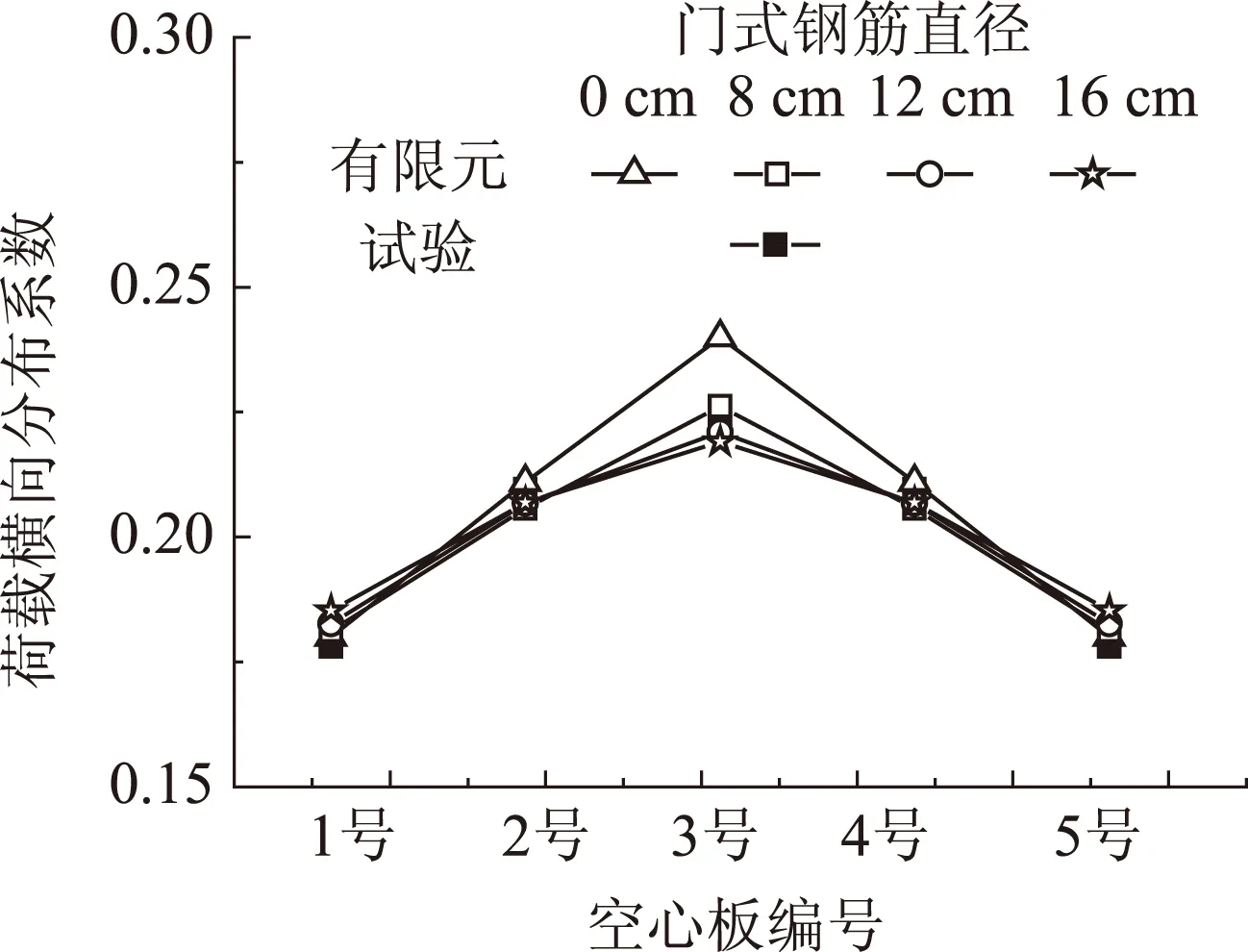
图16　不同门式钢筋直径下荷载横向分布系数Fig.16　Load transversal distribution factors with different diameters of gate-type steel rebar

3.3铰缝混凝土强度等级

根据前面的统计结果可知，新标准图中空心板和铰缝的混凝土材料范围为C30至C50混凝土。现将空心板与铰缝的混凝土取为C30，C40和C50，各项材料的强度、弹性模量按(JTG D62—2004)[12]的相关条文进行取值。将各个强度等级下结合面黏结滑移关系见图17～图19。

图17　C30混凝土黏结滑移关系曲线Fig.17　Curves of bonding-slip of C30 concrete

图18　C40混凝土黏结滑移关系曲线Fig.18　Curves of bonding-slip of C40 concrete

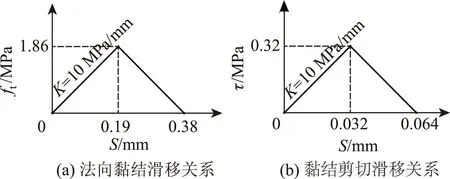
图19　C50混凝土黏结滑移关系曲线Fig.19　Curves of bonding-slip of C50 concrete

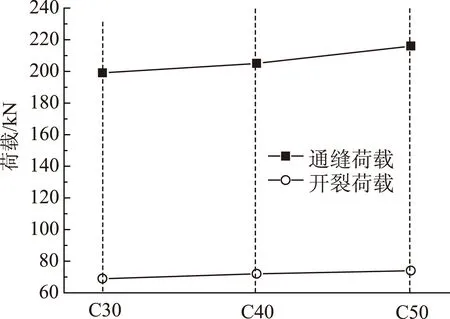
图20　不同混凝土强度下结合面开裂荷载和通缝荷载Fig.20　Crack loads and full-length crack loads of junction surface with different concrete strengths

图20和图21为不同混凝土强度下铰缝的开裂荷载、通缝荷载和裂缝分布。图22为不同混凝土强度下1号铰缝底部跨中处横向张开量曲线。可以看出，当混凝土强度等级从C30提高到C50时，结合面开裂荷载仅从69 kN提高至72 kN，提高7.2%；通缝荷载仅从199 kN提高至216 kN，提高8.5%；空心板与铰缝结合面竖向通缝沿纵桥向分布范围减小7.7%；结合面底部裂缝沿纵向分布范围减小10.2%；铰缝横向张开量减小10.5%。由于空心板与铰缝结合面是空心板桥最薄弱部位，在外荷载作用下，结合面先于铰缝和空心板开裂，然而提高混凝土强度对结合面黏结强度影响较小。因此，提高铰缝混凝土强度，对结合面开裂荷载、通缝荷载无明显改善，对结合面竖向通缝和结合面底部裂缝纵向分布、限制铰缝横向张开所起的作用较为有限。

图21　不同混凝土强度下竖向通缝和底部裂缝分布长度Fig.21　Lengths of vertical full-length crack and crack at bottom of junction surface with different concrete strengths

图22　不同混凝土强度下跨中铰缝横向张开量曲线Fig.22　Curves of transverse opening of hinged joint at mid-span with different concrete strengths

3.4空心板与铰缝结合面黏结力

结合面黏结力与结合面的粗糙程度等因素密切相关，本文通过调整黏结滑移刚度K来改变结合面黏结力的大小。根据前面的叙述可知，黏结滑移刚度K的取值范围为5～15 MPa/mm，现考虑K取5，10 MPa/mm和15 MPa/mm 3个数值，数值越大说明结合面黏结力越大。图23和图24为黏结滑移刚度为5 MPa/mm和15 MPa/mm的结合面黏结滑移曲线。

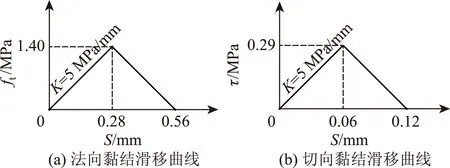
图23　黏结滑移刚度5 MPa/mm的黏结滑移曲线Fig.23　Bonding-slip curves with bonding-slip stiffness of 5 MPa/mm

图24　黏结滑移刚度15 MPa/mm的黏结滑移曲线Fig.24　Bonding-slip curves with bonding-slip stiffness of 15 MPa/mm

图25和图26表示了不同结合面黏结力下铰缝的开裂荷载、通缝荷载和裂缝分布。当黏结滑移刚度从5 MPa/mm增大到15 MPa/mm时，结合面开裂荷载从73 kN仅提高至76 kN，提高4.1%；结合面底部裂缝纵向分布长度从5.8 m仅减少至5.3 m，减小9.4%。这是由于即使提高铰缝与空心板结合面黏结力，结合面还是空心板桥最薄弱位置，在外荷载作用下，结合面仍然会先于空心板开裂。

图25　不同黏结滑移刚度下结合面开裂荷载和通缝荷载Fig.25　Crack loads and full-length crack loads of junction surface with different bonding-slip stiffnesses

图26　不同黏结滑移刚度下结合面竖向通缝和底部裂缝纵向分布长度Fig.26　Longitudinal lengths of vertical full-length crack and crack at bottom of junction surface with different bonding-slip stiffnesses

从图25和图26可以看出，当黏结滑移刚度从5 MPa/mm 增大到15 MPa/mm时，通缝荷载从184 kN 提高至212 kN，提高15.2%；结合面竖向通缝纵向分布范围从1.6 m减少至1.3 m，减小23%。这说明虽然提高结合面黏结力对提高铰缝开裂荷载减少底部裂缝纵向分布长度有限，但提高结合面黏结力可有效延缓裂缝开展。

因此，提高空心板与铰缝结合面黏结力，不能明显提高结合面开裂荷载，但可以提高结合面通缝荷载，并能减小结合面底部裂缝和竖向通缝纵向分布范围。

图27为铰缝跨中截面底部横向张开量曲线。可以看出，当黏结滑移刚度从5 MPa/mm增大到15 MPa/mm 时，铰缝横向张开量减少13.3%。由于提高空心板与铰缝结合面黏结力能有效延缓裂缝开展，减小通缝纵向分布范围，因此，该措施对限制铰缝横向张开也有一定的作用。

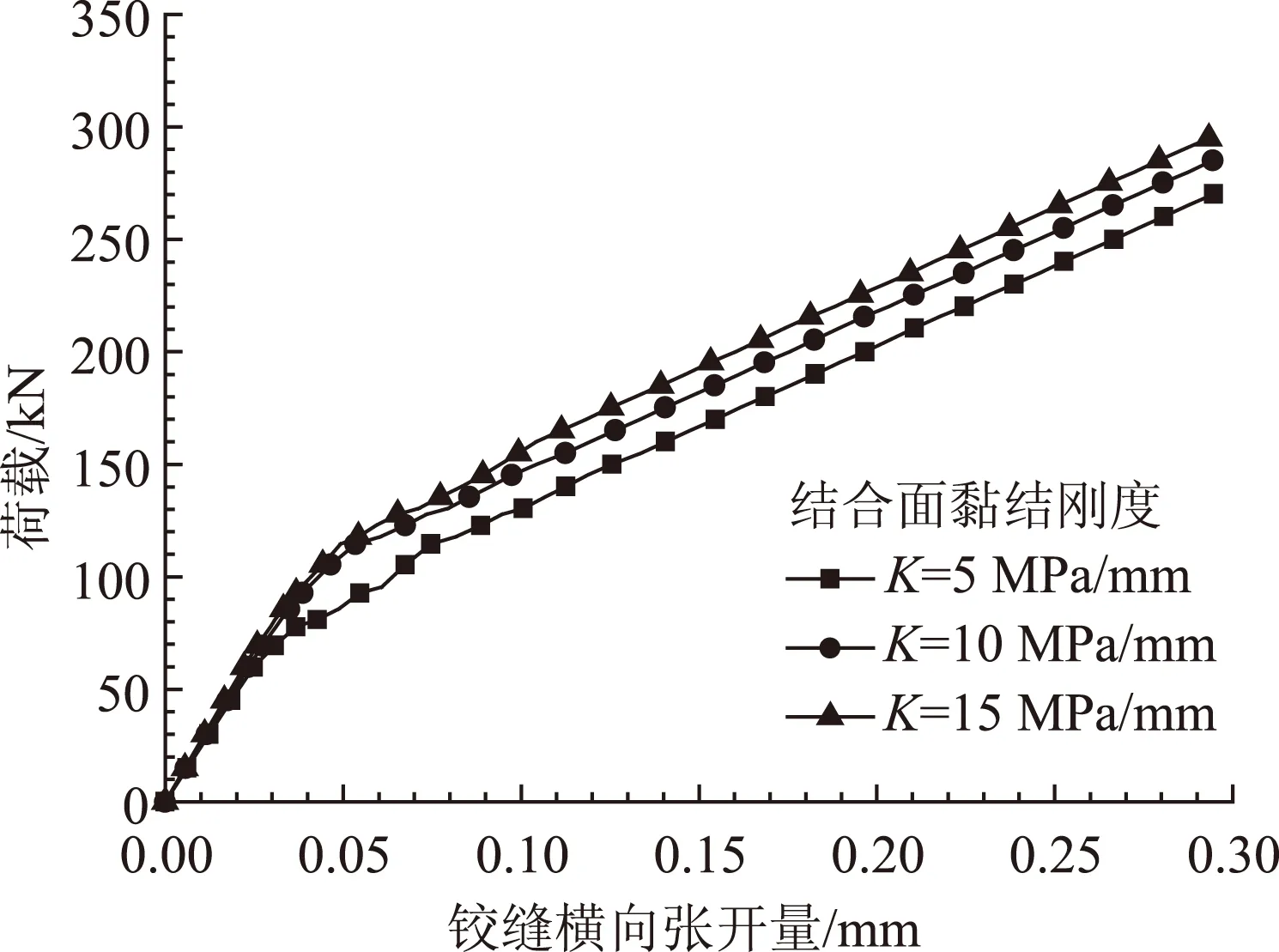
图27　不同黏结滑移刚度下铰缝跨中截面横向张开量曲线Fig.27　Curves of transverse opening at mid-span section of junction surface with different bonding-slip stiffnesses

4　对现有铰缝构造改进措施的讨论

4.1结合面构造钢筋

文献[20-22]提及了几种新型铰缝钢筋，见图28。图28(a)和(b)所示结合面构造钢筋类似于标准图中的门式构造钢筋，主要改变了空心板与现浇铰缝之间的锚固方式，包括构造钢筋角度、增设端部弯钩等。图28(c)是将构造钢筋延伸至相邻空心板顶部，以增加空心板、铰缝和桥面铺装的整体性。

图28　结合面构造钢筋Fig.28　Structural rebar at junction surface

结合3.1节的参数分析可知，由于空心板与铰缝结合面是空心板桥最薄弱位置，在外荷载作用下，结合面最先开裂破坏。因此，与门式构造钢筋相比，这3类铰缝钢筋仅改变空心板与铰缝连接方式的措施，对改善结合面受力性能有限，无法提高空心板与铰缝结合面的开裂荷载和形成竖向通缝的荷载，也无法改善结合面裂缝分布。

此外，结合3.2节的参数分析可知，增加结合面钢筋直径对结合面开裂荷载和通缝荷载无明显影响，对结合面裂缝分布所起的限制作用较为有限，因此，在实际应用中没有必要加大结合面门式构造钢筋的直径。

4.2铰缝内填材料

目前在国外填充剪力键最常用的材料为高强砂浆[23]，如果将高强砂浆应用在我国铰接空心板桥铰缝内填材料中，这类材料具有流动性好和现场施工工艺简便的特点[24]，可以解决空心板桥现场施工中铰缝混凝土由于钢筋密集难以振捣的缺陷，还具有与钢筋协同工作性能良好、耐久性良好的优点。同时，高强砂浆1 d抗压强度可达20 MPa，28 d抗压强度可大于60 MPa[24]。

根据3.3节的参数分析可知，如果仅仅是材料强度的提高，对整体结构最为薄弱的空心板与铰缝结合面的开裂荷载和通缝荷载无明显改善，对限制结合面竖向通缝和结合面底部裂缝沿纵向分布范围所起的作用较为有限。由于目前对高强砂浆与混凝土结合面的黏结滑移关系还未有深入的研究，因此需要先进行这方面的相关内容后方可进一步考虑高强砂浆在铰缝内填材料中的应用。

5　结论

由于空心板跨径和横桥向片数对铰缝与空心板受力性能及在各自极限荷载下的破坏模式影响较小，因此，本文以5片8 m跨径的带深铰缝构造的铰接空心板桥为研究对象，分析了不同铰缝构造参数对空心板桥铰缝和空心板破坏模式的影响，研究结论适用于各种跨径的铰接空心板桥。

(1)新标准图在空心板与铰缝结合面之间增设了8 mm门式钢筋，空心板与铰缝结合面开裂荷载仅提高4.5%，但是，结合面通缝荷载提高37.2%，结合面竖向通缝纵向分布范围减小72%，结合面底部通长裂缝减少48.1%。这说明在结合面底部增设门式钢筋，不能明显提高铰缝构造的开裂荷载，但可以提高铰缝构造的通缝荷载，延缓空心板与铰缝结合面竖向通缝和纵桥向通缝的形成。

(2)当空心板与铰缝结合面门式钢筋的直径由8 mm增大至16 mm，空心板与铰缝结合面开裂荷载提高4.3%，通缝荷载提高3.5%，结合面竖向通缝纵向分布范围减少16.7%，结合面底部裂缝纵向分布范围减少8%。这说明增大空心板与铰缝结合面构造钢筋直径对结合面开裂荷载、通缝荷载和最终的裂缝分布没有明显改善。

(3)随混凝土强度由C30提高至C50，空心板与铰缝结合面开裂荷载提高了7.2%，形成通缝的荷载提高了8.5%，结合面竖向通缝沿纵桥向分布范围减小了7.7%，结合面底部裂缝分布减小10.2%。这说明增大混凝土强度对空心板与铰缝结合面的改善作用有限。

(4)随结合面黏结滑移刚度由5 MPa/mm提高至15 MPa/mm时，空心板与铰缝结合面开裂荷载提高4.1%，通缝荷载提高15.2%，结合面竖向通缝纵向分布范围减小23%，结合面底部裂缝纵向分布范围减小9.4%。这说明提高空心板与铰缝结合面黏结力可提高结合面通缝荷载，并能减小裂缝分布范围。

(5)现有文献提及的3种铰缝钢筋布置形式和增大钢筋直径的方法较难从根本上改善结合面受力性能。

References:

[1]陈宝春，陈友杰. 桥梁工程[M]. 北京：人民交通出版社，2013.

CHEN Bao-chun, CHEN You-jie. Bridge Engineering [M]. Beijing: China Communications Press, 2013.

[2]凌伟, 黄卿维, 彭桂瀚, 等. 某高速公路铰接简支板桥病害调查分析[C] // 第11届全国建筑物鉴定与加固改造学术交流会议论文集. 北京: 中国建材工业出版社, 2012: 487-491.

LING Wei, HUANG Qing-wei, PENG Gui-han, et al. Disease Investigation and Analysis of an Expressway Fabricated Simply Supported Slab Bridge[C]//Proceedings of 11th National Academic Exchange Conference about Building Appraisal and Reinforcement Transformation. Beijing: China Building Materials Industry Press, 2012: 487-491.

[3]王渠, 吴庆雄, 陈宝春. 装配式空心板桥铰缝破坏模式试验研究[J]. 工程力学, 2014, 31(增1): 115-120.

WANG Qu, WU Qing-xiong, CHEN Bao-chun. Experimental Study on Failure Mode of Hinged Joint in Assembly Voided Slab Bridge [J]. Engineering Mechanics, 2014, 31(S1): 115-120.

[4]陈悦驰, 吴庆雄, 陈宝春. 装配式空心板桥铰缝破坏模式有限元分析[J]. 工程力学, 2014, 31(增1): 51-58.

CHEN Yue-chi, WU Qing-xiong, CHEN Bao-chun. Failure Mode of Hinged Joint in Assembly Voided Slab Bridge by Finite Element Analysis[J]. Engineering Mechanics, 2014, 31(S1): 51-58.

[5]吴庆雄，陈悦驰，陈康明. 结合面底部带门式钢筋的铰接空心板破坏模式分析[J]. 交通运输工程学报，2015, 15(5): 15-25.

WU Qing-xiong, CHEN Yue-chi, CHEN Kang-ming. Failure Mode Analysis of Hinged Voided Slab with Gate-type Steel Rebars at Bottom of Junction Surface [J]. Journal of Traffic and Transportation Engineering, 2015, 15(5): 15-25.

[6]王峰. 桥面整体化铺装层加固后空心板梁受力性能研究[D]. 福州：福州大学, 2012.

WANG Feng. Research on Mechanical Behavior of Hinged Voided Slab Bridge with Reinforcement of Integration Pavement [D]. Fuzhou: Fuzhou University, 2012.

[7]姜云霞，柴金义，伍必庆，等. 不中断交通实施铰接板桥加固的研究[J]. 内蒙古公路与运输，2002(2)：1-3.

JIANG Yun-xia, CHAI Jin-yi, WU Bi-qing, et al. Research on Strengthening Hinged Slab Bridge under Uninterrupted Traffic [J]. Highways & Transportation in Inner Mongolia, 2002(2): 1-3.

[8]JTJ 023—85, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

JTJ 023—85, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S].

[9]JTJ 021—89, 公路桥涵设计通用规范[S].

JTJ 021—89, General Code for Design of Highway Bridges and Culverts [S].

[10]JT/GQB002—93, 公路桥涵标准图 铰接钢筋混凝土斜空心板桥上部构造[S].

JT/GQB002—93, Standard Drawings for Highway Bridges and Culverts: Superstructure of RC Skew Hinged Voided Slab Bridges [S].

[11]JT/GQB001—93, 公路桥涵标准图 铰接预应力混凝土斜空心板桥上部构造[S].

JT/GQB001—93, Standard Drawings for Highway Bridges and Culverts: Superstructure of Prestressed Skew Hinged Voided Slab Bridges [S].

[12]JTG D60—2004, 公路桥涵设计通用规范[S].

JTG D60—2004, General Code for Design of Highway Bridges and Culverts [S].

[13]JTG D62—2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

JTG D62—2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts [S].

[14]中华人民共和国交通部. 公路桥涵通用图[M]. 北京：人民交通出版社，2007.

Ministry of Transport of PRC. Standard Drawing of Highway Bridge [M]. Beijing: China Communications Press, 2007.

[15]GB 50010—2002, 混凝土结构设计规范[S].

GB 50010—2002, Code for Design of Concrete Structures [S].

[16]秦德生. 板式橡胶支座力学性能试验研究及数值模拟[D]. 大连：大连理工大学，2008.

QIN De-sheng. Test Research and Numerical Simulation of Mechanical Properties of Plate Type Elastomeric Pad Bearings [D]. Dalian: Dalian University of Technology, 2010.

[17]刘健. 新老混凝土粘结的力学性能研究[D]. 大连：大连理工大学，2000.

LIU Jian. Study on Mechanics Performance of Adherence of Young on Old Concrete [D]. Dalian: Dalian University of Technology, 2000.

[18]刘沛林. 装配式钢筋混凝土简支板梁桥铰缝受力性能研究[D]. 北京：清华大学，2010.

LIU Pei-lin. Study on Mechancal Behaviors of Hinge Joints for Fabricated Reinforced Concrete Simply-supported Plate Girder Bridges [D]. Beijing: Tsinghua University, 2010.

[19]叶见曙，刘九生，俞博，等. 空心板混凝土铰缝抗剪性能试验研究[J]. 公路交通科技，2013, 30(6)：33-39.

YE Jian-shu, LIU Jiu-sheng, YU Bo, et al. Experiment on Shear Property of Hinge Joints of Concrete Hollow Slab[J]. Journal of Highway and Transportation Research and Development, 2013, 30(6): 33-39.

[20]陈建华. 空心板梁桥单片梁受力分析及预防措施[J].中外公路，2007(3): 118-121.

CHEN Jian-hua. Force Analysis and Prevention Measures on Single Beam of Voided Slab Bridge[J]. Journal of China & Foreign Highway, 2007(3): 118-121.

[21]张志. 空心板铰缝破坏机理及防治措施研究[J]. 山西建筑, 2009, 35(2): 318-320.

ZHANG Zhi. Research on Failure Mechanism and Preventing Measures of Hinged Joint of Voided Slabs [J]. Shanxi Architecture, 2009, 35(2): 318-320.

[22]黄德耕. 广西装配式空心板桥梁设计研究[D]. 南宁：广西大学，2008.

HUANG De-geng. Design Research on Assembly Voided Slab Bridge in Guangxi [D]. Nanning: Guangxi University, 2008.

[23]HANNA K E. Behavior of Adjacent Precast Prestressed Concrete Box Girder Bridges [D]. Lincoln: University of Nebraska, 2008.

[24]薄祥照. HGM 高强无收缩灌浆材料的研制与应用[J]. 国防交通工程与技术, 2006, 4(3): 58-60.

BO Xiang-zhao. The Development and Application of the HGM High-Strength Shrinkage-Free Grouting Material[J]. Traffic Engineering and Technology for National Defense, 2006, 4(3): 58-60.

Parameter Analysis on Mechanical Property of Hinged Hollow Slab Bridge with Gate-type Steel Bars at Bottom of Junction Surface

CHEN Kang-ming, WU Qing-xiong, HUANG Wan-kun, CHEN Bao-chun

(School of Civil Engineering, Fuzhou University, Fuzhou Fujian 350116, China)

In order to study the mechanical performance of hinged joint in hinged hollow slab bridge with gate-type steel rebar, taking the hinged hollow slab bridge with full-depth hinged joint structure as study object, the evolution of hinged joint structure in Chinese hinged hollow slab bridges is summarized, and the parameter analysis for a hollow slab bridge with a span of 8 m is conducted by nonlinear finite element method. The failure mode of the hinged joint structure with different parameters, including crack load and distribution of cracks, is studied, and the improving countermeasures of existing hinged joint structures are also discussed. The result shows that (1) adopting gate-type steel rebar at the bottom of junction surface cannot obviously improve the crack load of hinged joint, but it can delay the occurring of the full-length cracks of junction surface between hollow slab and hinged joint as mell as the longitudinal full-length cracks; (2) increasing the diameter of gate-type steel rebar cannot obviously improve the crack load of junction surface and the load of full-length crack and the final distribution of cracks; (3) enhancement of concrete strength cannot obviously improve the mechanical property of the junction surface;(4) the enhancement of the bound strength of the junction surface can improve the full-length crack load of the junction surface and reduce the distribution of cracks; (5) 3 layouts of the reinforcement in hinged joint and increasing diameter of steel rebar proposed in the existing references would not fundamentally improve the mechanical property of junction surface.

bridge engineering; hinged hollow slab bridge; parameter analysis; hinged joint structure; gate-type steel bar; nonlinear finite element

2015-11-06

教育部新世纪优秀人才支持计划项目(NCET-13-0737)；河北省交通运输厅2011年度科技计划项目(Y-2011023)

陈康明(1985-)，男，福建霞浦人，博士，助理研究员.(chen-kang-ming@163.com)

U443.3

A

1002-0268(2016)08-0065-11

doi:10.3969/j.issn.1002-0268.2016.08.011