研究试题特征,把握复习方向
2016-08-23浙江省杭州市江干区教育发展研究院易良斌
□浙江省杭州市江干区教育发展研究院 易良斌
筅新卷首
研究试题特征,把握复习方向
□浙江省杭州市江干区教育发展研究院 易良斌
各地中考数学试题主要考察十大核心概念。试题回归四基,紧扣教材,体现探索图形的形成过程,关注研究函数问题的基本方法,指向学科综合学习。把握这些特征,有助于把握中考命题规律,有效复习备考。
中考试题 试题特征 复习建议
中考数学试题命题改革应有利于切实减轻中学生过重的学业负担,有利于引导学校深入实施素质教育,推进课程教学改革,有利于培养学生的创新精神和实践能力,促进学生健康成长和全面和谐、富有个性的发展。
一、中考数学考试的基本理念、主要内容与要求
基本理念:体现《义务教育数学课程标准(2011年版)》所确立的课程评价理念,从知识技能、数学思考、问题解决、情感态度四个方面进行评价,注重整体性、综合性与实践性,突出对学生数学素养的全面考查。
内容与要求:课程标准中“课程内容”部分规定的“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四个领域的内容。主要考查的方面包括:基础知识,基本技能,基本思想,基本活动经验;数学思考,发现、提出并分析、解决问题的能力;创新意识和科学的态度等。关注并体现的方面包括:数感,符号意识,空间观念,几何直观,数据分析观念,运算能力,推理能力,模型思想,应用意识和创新意识等。设计一定的结合实际情境的问题、开放性问题、探究性问题、对学生学习过程考查的问题等,以体现对学生相关数学能力的考查。注重通用通法,淡化特殊的解题技巧,适当控制运算量。
二、中考数学试题的一般特点
1.紧扣《课标》:一般不允许超出《课标》要求。
2.源于教材:为体现试题素材的公平性,一般题目尽量来源于教材。
3.覆盖面广:一般教材“章”的覆盖率要达到100%,重点内容重点考查。
4.联系实际:一般有30%~40%的联系当前热点的实际应用题,着重考查学生解决实际问题的能力。
5.突出方法:一般注重数学思想方法的考查,重点考查数形结合、方程、函数、转化、数学建模、分类讨论等数学思想方法的考查。
6.体现探究:一般围绕初中数学中的重点内容设置形式多样的探究性问题,着重考查学生分析问题和解决问题的能力。
7.难易适度:一般要求得分率为75%~85%。
8.梯度呈现:一般设置有基础题、中档题和压轴题,由易到难,梯级呈现,以便区分不同层次的学生。
三、中考数学特色试题分析
近几年的中考试题立足基础,突出重点,能力立意,考查学生对基本数学知识、方法的理解与掌握情况,考查学生运用数学思想的状况,考查学生的数学能力及数学学习潜能,从而检测学生已有的和潜在的后续学习能力,体现考基础、考能力、考素质的考试目标,达到有利于引导和促进数学教学全面落实《数学课程标准》所设立的课程目标,有利于更新教师的课堂教学观念,改进教师的教学行为,有利于改善学生的数学学习方式。
1.试题回归四基,紧扣教材。
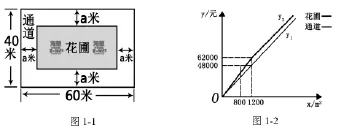
【例1】(2015广西南宁)如图1-1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米。
(1)用含a的式子表示花圃的面积;
(3)已知某园林公司修建通道、花圃的造价y(1元)、y2(元)与修建面积x(m2)之间的函数关系如图1-2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
分析:(1)用含a的式子先表示出花圃的长和宽后利用其矩形面积公式列出式子即可;
(3)根据图象,设出通道和花圃的解析式,用待定系数法求解,再根据实际问题写出自变量的取值范围即可。
【评析】本题考查了一次函数的应用及一元二次方程的应用,解题的关键是表示出花圃的长和宽。试题源于教材、高于教材。
2.试题体现探索图形的形成过程。
【例2】(2015湖南岳阳)已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点。
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA 与PB的数量关系:。
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由。
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA·PB=k·AB。

分析:(1)根据三角形CBD是直角三角形,而且点P为线段CD的中点,应用直角三角形的性质,可得PA=PB,据此解答即可。
(2)首先过C作CE⊥n于点E,连接PE,然后分别判断出PC=PE、∠PCA=∠PEB、AC=BE;然后根据全等三角形判定的方法,判断出△PAC∽△PBE,即可判断出PA=PB仍然成立。
(3)首先延长AP交直线n于点F,作AE⊥BD于点E,然后根据相似三角形判定的方法,判断出△AEF∽△BPF,即可判断出AF·BP=AE·BF,再个AF=2PA,AE=2k,BF=AB,可得2PA·PB=2k.AB,所以PA·PB=k·AB,据此解答即可。
【评析】此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从图象中获取信息,并能利用获取的信息解答相应的问题的能力;考查了直角三角形的性质和应用,要熟练掌握;考查了全等三角形的判定和性质的应用,以及相似三角形的判定和性质的应用,要熟练掌握。
3.试题关注研究函数问题的基本方法。
【例3】(2014浙江杭州)复习课中,教师给出关于x的函数y=2kx2-(4k+1)x-k+1(k是实数)。
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上。
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:
(1)存在函数,其图象经过(1,0)点;
(2)函数图象与坐标轴总有三个不同的交点;
(3)当x>1时,不是y随x的增大而增大就是y随x的增大而减小;
(4)若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数。
【评析】试题的四条结论,分别涉及方程思想求解析式、图象与坐标轴交点问题、函数单调性讨论、函数最值等问题,覆盖到函数的解析式、图象和性质,问题设计立足基础,考查考生对基础知识的灵活应用,也在一定程度上考查了考生的知识迁移能力和灵活应用能力。问题看似相互独立,实则可上下联系,体现人文关怀,有利于学生充分发挥自己真实的数学水平,作为压轴题,这样的设计可谓高明。
4.试题指向学科综合学习。
【例4】(2015湖北荆州)如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点。
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。

【评析】试题考查了二次函数的综合应用,要求熟练掌握用待定系数法求二次函数解析式、二次函数的性质和相似三角形的判定与性质;掌握平行四边形的性质点、平移的规律;会证明圆的切线。
四、中考数学复习教学建议
1.重视学生数学素养的培养。从关注学生的主体性着手,重视学生数学基本活动经验的积累。培养学生的空间观念和逻辑思维能力,从而促进知识的动态生成和学生数学思维的深度。学生只有具备敏锐的数学眼光,才能识别出题目中的有效信息。与此同时,细致耐心的做题态度也是不可或缺的。学生在平时的学习中要有意识地注重细节,养成良好的数学学习习惯。
2.加强知识联系与应用的教学。概念是数学知识体系的基本单位,学生在学习时,对相似的概念和性质容易混淆,对概念、公式、定理掌握不到位是影响学生解题的症结所在。因此,在概念教学中,要对各个概念、公式和定理进行串联、总结,将新学知识与其他知识发生多向联系,用图示等多种方式表征数学,采用开放性问题等,帮助学生厘清相关知识之间的区别与联系,从而做到对概念、定理和公式的透彻理解和灵活运用。
3.重视综合实践活动教学。“综合与实践”是以问题为载体,以学生自主参与为主的学习活动。综合与实践活动是以长作业的形式出现,将课堂内的数学活动延伸到课堂外,让学生经历收集数据、查阅资料、独立思考、合作交流、推理论证等多种形式的活动。为此,教师在教学中要结合具体的课程内容,精心设计一些能利用这些知识进行的探索活动,这些活动每位学生都能参与,不同的学生可以通过解决问题的过程,获得不同的体验。通过学生动脑、动手、动口,构建学生自主探索、全过程参与获取知识的平台,使学生有经历观察、猜测、计算、推理等活动的过程。本着“积累数学活动经验,培养应用意识和创新意识”的重要目标,既重在实践,又重在综合,注重数学与生活实际、数学与其他学科、数学内部知识的联系和综合应用,感受数学的理性精神和人文价值。
