基于多项式曲线拟合的二次雷达系统译码门限优化方法

李建秋 何 川 常俊飞 王世民

(四川九洲空管科技有限责任公司绵阳 621000)

信号数据处理

基于多项式曲线拟合的二次雷达系统译码门限优化方法

李建秋 何 川 常俊飞 王世民

(四川九洲空管科技有限责任公司绵阳 621000)

针对传统二次雷达系统阵地优化中译码门限的产生依赖工程经验，不能实时有效地抑制因阵地环境因素产生的虚假目标的现象，本文提出了二次雷达系统译码门限的自动拟合生成与优化调整方法，该方法采用了多项式拟合理论和最佳逼近理论，工程实现中将门限曲线通过优化软件按不同扇区导入，并依据目标虚警概率和点航迹效果对译码门限进一步优化调整。仿真结果验证了本文算法的有效性，实际工程的应用验证了本文提出的译码门限优化方法能很好的抑制杂波干扰，能有效剔除虚假目标。

二次监视雷达;目标点迹处理;译码门限;最小二乘法;多项式曲线拟合

0 引 言

二次雷达在阵地架设完毕后需要根据实际军事任务及性能的需求进行阵地现场优化［1－2］。在阵地现场优化过程中，需要综合考虑影响二次雷达实际性能的阵地问题，主要包括阵地所处的地理位置、电磁环境、气象、障碍物等环境因素［3］。根据对二次雷达实际战技术指标的要求，选择合理的优化措施，对雷达装备系统状态、各项参数等进行优化设置和调整，最大限度消除地物、气象和电磁干扰等带来的影响，从而尽可能提高雷达装备的战技术性能［3］，实现装备、阵地环境的最佳匹配，尽而发挥出雷达的最大作战效能，为战场指挥和战略决策提供依据。

在传统的二次监视雷达阵地现场优化中，译码门限参数的优化调整依赖有经验的工程师。这种方式主观性强，无法对调整的效果进行有效的评估，而且大部分优化操作步骤复杂，优化是一个反复调整的过程。因此同型号的雷达由于架设阵地的不同，要达到预期的效果往往需耗费大量的时间、人力和物力，而且优化效率低下。若在战备期，就会严重影响雷达实时作战使用［3］要求，贻误战机。

针对当前国内全固态二次监视雷达系统在阵地优化中译码门限调整中主观性较强，参数值配置全凭经验，优化架设成本高，对串扰、异步干扰、反射干扰引起的较多虚假信号不能有效抑制以及优化效率低的问题［4－6］。本文提出了一种基于最小二乘法多项式曲线拟合的方法［10］［12］，该方法根据录取的应答目标数据自动拟合生成译码门限［13］曲线，并根据点航迹效果和虚假目标的剔除效果进行译码门限的自动优化调整，实现在符合期望虚警概率［11］条件下的译码门限自动优化，为二次雷达后端的目标数据处理提供很重要的参考。通过实际工程的应用，本文提出目标译码门限的拟合生成及优化方法，具有灵活高效、优化调整方便、快捷的特点，并可实时检验优化效果，能很好的抑制近端的反射，串扰等杂波干扰，能有效剔除虚假目标，在实际阵地优化中取得了良好的效果，大大提高了优化的效率，减少了雷达架设过程中的人力、物力、财力成本。

1 二次雷达阵地优化处理模型

影响二次雷达译码的常见环境因素有阵地所处的地理位置、电磁环境、气象、障碍物等，那么我们就可以在点迹处理时根据不同地理环境选择不同的译码门限。译码门限的主要作用是在点迹处理中抑制译码门限以下的虚假目标，检测出译码门限以上的有效目标并进行译码处理。译码门限工作示意图如图1所示。

图1 译码门限作用示意图

译码门限是二次雷达后端点迹处理中剔除虚假目标的重要判定依据，译码门限的自动、快速生成与优化调整是提高阵地优化效率的重要方法之一。二次雷达阵地优化处理流程包括，应答机标校、接收机参数优化、译码参数优化等，整改系统阵地优化流程如图2所示。其中译码门限优化流程如图中黑色部分所示。

图2 二次雷达阵地优化中译码门限优化流程图

2 译码门限曲线拟合的数据处理

2.1 多项式拟合和最佳逼近理论

在实际工程中译码门限代表了探测距离与目标阀值信息，为了从观测目标的阈值和距离之间的寻求出函数关系，结合实际中观测数据分布特点，本文选择多项式模型进行拟合，模型如下:

为了评估拟合效果，引入误差评估因子，如下:

表示理论值与观测值间的差值的平方和的统计平均。满足最小的函数是观测数据的最佳拟合曲线。

求解(1)式的最佳拟合曲线等价于解方程组［10］(3)式的最佳逼近解。

其中令A∈cm×(n+1)，是式(3)左端的系数矩阵，y是式(3)右端的向量，解向量为β=(β0，β1，…，βn)T。

实际工程中式(3)中的线性方程组往往是不相容的，根据广义逆矩阵的理论可知，对于不相容方程组Ax=y的最小二乘解，改写如下:

其中A+是广义逆矩阵，(4)式方程组的最小二乘解是唯一的，而且还是最佳的。

2.2 算法处理流程

根据上述的最佳逼近理论和广义逆矩阵的求解理论［10］，本文中译码门限的拟合算法的处理流程如图3所示。

图3 译码门限拟合算法处理流程图

由图3可知，译码门限的生成和优化调整主要分包括以下步骤:

步骤一:原始观测数据录取。实时接收阵地优化中接收机中频数字化处理后的观测数据。

步骤二:数据预处理。根据采集的原始观测数据构造多项式线性方程组的系数矩阵A。对原始数据中的“野值”，即在边界点幅度变化异常的数据进行剔除，同时构造矩阵A成为列或行满秩的矩阵。

步骤三:多项式拟合求解。对满足步骤二的矩阵求出A+，进而求出最佳逼近解。

步骤三:门限曲线生成。根据求出的最佳逼近解生成门限曲线。

步骤四:拟合误差分析。根据拟合平滑效果和拟合值与观测值间的差值，初步确定效果较好的迭代次数n的范围。

步骤五:导入扇区。按拟合数据的范围，导入相应的扇区。

步骤六:综合评估。通过二次雷达显控软件的目标点航迹显示与虚警概率统计功能进行综合评估，若虚警率高或点迹连续性和凝聚效果差，说明抑制门限较低不能很好抑制虚假目标，则给出门限曲线整体幅度上调参数Δ和迭代次数n，首先确定上调幅度参数Δ，对比几组n;在综合考虑运算量的实时性和最终效果的要求下，最终确定迭代次数n。

结合二次距离分辨力参数，在工程中Δ选择在0m至5m，n小于10次。

3 仿真及分析

本文中采用的仿真数据来自于二次雷达近端50Km范围内录取的50组应答目标数据，其中数据是二维的，表示飞行目标的距离和幅度的关系，采用Matlab进行拟合建模、分析论证和优化调整［12，14，16］。仿真结果的分析依据误差因子［9］和曲线拟合的平滑度，当越小，平滑度越好，拟合效果越好。

按照译码门限拟合算法流程，通过多项式线性方程组建模求解与拟合仿真。仿真结果发现当拟合次数n为0、1、2时，模型退化为直线无法拟合，分别为4.3485e－017、46.7117、34.7575;n为3时，σ=11.5726曲线在50Km不收敛;n为4、5、6、7拟合效果较好，σ分别为 0.0022、0.0045、0.6036、0.6958;当n为8、9、10时曲线平滑度下降部分曲线呈扭曲形状，σ分别为0.5250、0.1512、0.00264。当n大于10以上，拟合曲线与原始数据几乎重合，σ变的更小，曲线扭曲度高而平滑性效果差，但这种效果是不需要的，在实际中扭曲部分会引入虚假目标。其中拟合12次时形成的译码门限如图7所示。而且随着拟合次数的增加计算量增加。

因此本文给出当拟合次数为4次，即此时多项式模型为y=β0+β1x+β2x2+β3x3的拟合曲线，仿真结果如图4、图5和图6所示。其中图4是原始录取数据与预处理后的结果。图5应用最小二乘法多项式拟合的结果、以及与预处理后的数据差值曲线。图6是根据虚警概率［15］对拟合曲线微调形成的译码门限曲线。

图4 原始数据与经预处理后的数据曲线

图5 预处理后的数据、拟合数据和差值曲线

图6 根据虚警概率调整后形成的译码门限

当拟合12次时形成的译码门限，如图7所示。

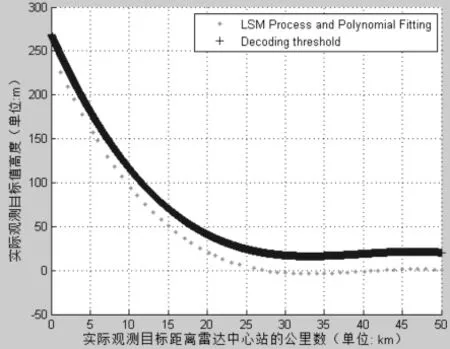
图7 根据虚警概率调整后形成的译码门限(拟合12次)

结合误差估计和曲线平滑度初步确定拟合迭代次数n可选择范围为4、5、6、7。为了使产生的拟合译码门限更加合理，后续根据实际工程中虚假目标出现的概率或者真实目标点迹凝聚的连续信息来最终确定可选范围内的拟合迭代次数n和微调量Δ。

4 工程应用

为了验证算法在二次雷达系统阵地优化中拟合算法的有效性和实用性，作者将算法应用于工程中并集成开发了相应的译码门限优化软件。该软件提供二次雷达威慑作用距离内［15］的原始应答数据采集、分析、生成、门限调整、数据保存以及加载应用功能。二次雷达点迹处理根据译码门限曲线参数对目标信号进行实时检测和译码处理，有效地将低于门限的杂波数据［8］进行抑制。与传统阵地优化方法相比，本文提出的方法具有灵活高效、优化调整方便快捷的特点，并可实时检验优化效果的特点。

数据录取完毕后，图形区域会显示目标数据的“距离－幅度”分布图形如图8所示。

译码门限拟合生成并微量调整后，按不同扇区导入的功能如图9所示。

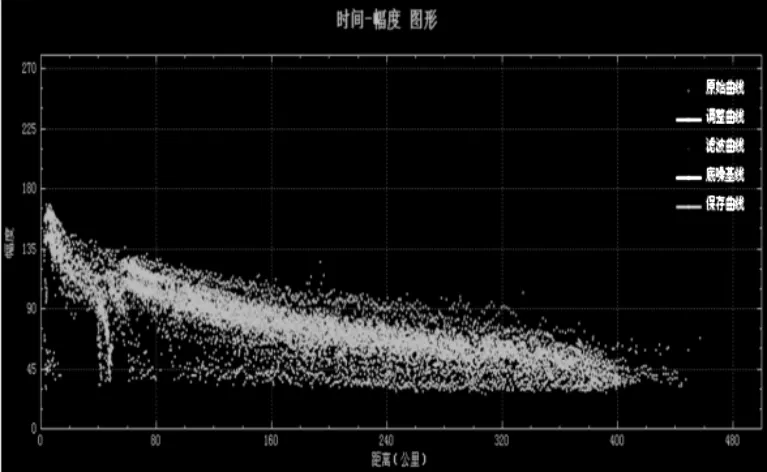
图8 目标“距离－幅度”分布图形显示

图9 译码门限按扇区导入示意图

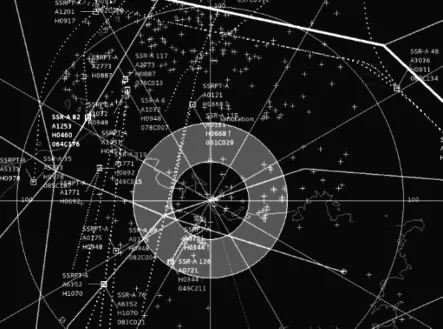
图10 受杂波干扰的目标点迹图

图11 译码门限抑制杂波干扰后的点迹图

工程中根据终端目标显示的点迹信息可判断出译码门限［15］的有效性。其中图10为受杂波干扰的点迹图，杂波点用“+”表示。图11为使用译码门限抑制杂波干扰后的点迹图，对比分析出译码门限使得虚假目标得到了有效地抑制和剔除，真实目标点航迹显示连续，充分验证了本文方法的有效性和实用性。

5 结束语

本文研究了一种用于二次监视系统阵地优化中译码门限曲线的拟合方法，为后端数据的译码处理提供了重要依据。通过对自动录取的应答目标数据预处理后，结合工程的目标数据的分布特点，采用多项式曲线为拟合模型，并应用矩阵理论中最小二乘法求解不相容线性方程组的最佳逼近解，其中广义逆矩阵的求解是关键。论证中采用Matlab软件对真实录取数据进行建模与仿真，保证了理论正确性。

为了验证本算法的实用性，在实际工程中集成开发了译码门限优化软件，解决了传统阵地优化中靠人工手动、耗时、高成本、凭工程经验进行抗杂波抑制的方式，同时解决了由于雷达架设阵地的不同而带来的反复优化调试的低效率工作方式。

本文的工作只是针对二次监视系统的阵地优化中译码门限的曲线拟合算法进行理论和实践应用的研究，而阵地优化中，绘制阵地遮屏蔽图、发射、接收优化、点迹优化、系统性能评估优化等其它问题有待进一步研究。特别是在本方法中拟合次数的不同效果不同，带来的计算量成倍增加，要根据雷达终端真实目标显示的点迹信息、虚警概率等因素合理选择拟合次数和微调量。同时，在拟合中数据的预处理显得尤为重要，特别是目标数据的个别“野值”会影响拟合效果。因此，原始录取数据的预处理方法有待进一步研究。

［1］陈辉，林强，贾晶，李陆军.雷达阵地现场优化评估理论体系研究［J］.电子信息对抗技术，2013，1(28):54－57.

［2］王中杰，刘海军，黄炜.一种雷达阵地优化的新方法［J］.现代雷达2015，9(37):26－28.

［3］雷达抗干扰效能评估指标体系及方法研究［D］成都电子科技大学电子工程学院，2008.

［4］STEVENS M C.Secondary surveillance radar［M］.Boston Artech House，Inc，1988.

［5］ICAO.Aeronautical Surveillance Manual［S］.First Edition，2009.

［6］中国民用航空总局.MH/T4010－2006空中交通管制二次监视雷达设备技术规范［S］.2006.

［7］BANAJI D.PLL Performance，Simulation，and Design［M］.Second Editoin，USA:National Semiconductor，2001:152－158.

［8］Y.T.Chan，K.C.Ho.A Simple and Efficient Estimator for Hyperbolic Location.IEEE Tran.on signal processing.1994，42(8):1905－1915.

［9］VOELKER K.Apply Error Vector Measurements in Communications Design［J］.Microare＆RF.1995(12): 30－33.

［10］黄廷祝，钟守铭，李正良.矩阵理论［M］.第三版.北京:高等教育出版社，2003(10):207－231.

［11］(美)Schonhoff，T.(美)Giordano，A.A.Dection and Estimation:Theory and Its Applications(信号检测与估计－理论与应用)［M］.第三版.北京:电子工业出版社，2012(1):323－348.

［12］陈光，任志良，孙海柱.最小二乘曲线拟合及Matlab实现［J］.兵工自动化软件技术，2005，24(3):107－108.

［13］丁鹭飞，耿富录.雷达原理［M］.第三版.西安:西安电子科技大学出版社，2002，6(3):49－51.

［14］刘海香.散乱数据点曲线拟合的研究及二次曲线拟合的一种新方法［D］.山东大学，2005，04.

［15］张尉，徐炎祥.二次雷达原理［M］.北京:国防工业出版社，2009(5):110－113.

［16］张峰.雷达阵地杂波测量和动态STC建立方法［J］.现代雷达，2014，4(4):10－13.

Method of Optimizing Decoding threshold in Secondary Surveillance Radar System Based on Polynomial Curve Fitting

Li Jianqiu，He Chuan，Chang Junfei，Wang Shimin
(Sichuan Jiuzhou ATC Technology Co.，Ltd.，Mianyang 621000，Sichuan)

Aiming at false target phenomenon caused by site environment factor which cannot be suppressed effectively in real time by depending on engineering experience achieved in generation of decoding threshold in traditional secondary surveillance radar system site optimization，a method of automatic fitting generation and optimization adjusting for decoding threshold in secondary radar is presented.This method is to introduce threshold curve according to different sector by optimizing software in engineering implementation by employing polynomial fitting theory and best approximation theory，optimizing adjust decoding threshold further according to target false alarm probability and plot/track effect.The simulated result verifies effectiveness of the presented algorithm.And application in practical engineering verifies that using decoding threshold optimizing method can suppress clutter interference better and eliminate false target effectively.

secondary surveillance radar;target plot processing;decoding threshold;Least squares method;polynomial curve fitting

TN952

A

1008-8652(2016)04-041-06

2016-07-20

李建秋(1979－)，男，硕士研究生。主要研究方向为监视雷达系统与西方体制敌我识别。